好きな証明 Advent Calendar 2018 の13日目の記事です。
好きな証明 Advent Calendarということで,私が今年になってから勉強し始めた「ガロア表現」という分野の定理の中で,特に面白いと思った証明を紹介したいと思います。
動機と参考文献
きっかけは以前から勉強していた 岩澤理論 でした。どうしても理解したい定理 があって,その証明にガロア表現が出てきます。
特に今回のテーマである 「ガロア表現の同値性」 が関わってくるのですが,その同値性を示すのにどうやら 「Chebotarevの密度定理」(あとで出てきます)が使えるらしいのです。
私の印象ですが,割とこの辺の知識は常識みたいに扱われることが多く,証明にも空気のように「Chebotarevの密度定理より」と書いてあったりします。いったいどうしてChebotarevの密度定理が使えるのかと不思議に思っていました。
しばらく勉強していくうちに,ガロア表現の同値性にChebotarevの密度定理が関係する「理屈」がわかってきました。そのことがとても嬉しくてこの記事を書いています。
私が勉強しているのは,整数論サマースクールの記事3つです。これらが今回の記事の参考文献になります。
http://www.math.sci.osaka-u.ac.jp/~ochiai/ss2009proceeding/ss2009preparation.pdf
[2] 山内 卓也:ガロア表現の基礎 I
http://www.math.sci.osaka-u.ac.jp/~ochiai/ss2009proceeding/ss2009yamauchi.2010-2-13.pdf
[3] 千田 雅隆:ガロア表現の基礎 II
http://www.math.sci.osaka-u.ac.jp/~ochiai/ss2009proceeding/summer-school.pdf
今回書いている内容は,基本的には上のPDFのどれかに書かれていることです。そのため,内容を正確に知りたい人は上のPDFを読むのが一番いいと思います。
そういった意味でこの記事の価値がどこにあるのかよくわかりませんが,でもどうしても書きたくなっちゃったので仕方ありません。
1節で基本的な事項をさらってから,2節で本題の「ガロア表現の同値性」について,3節で「Chebotarevの密度定理」について紹介します。
4節・5節でChebotarevの密度定理がどのように証明に使われるのか説明して,6節で証明のキーポイントを説明して終わります。
「ガロア表現とか難しい!ぜんぜん分からないよ!」という方は6節だけでも読んでいただけると嬉しいです。
それでは,少し長くなりますがお付き合いください。
1.ガロア表現とは(前提知識)
そもそもガロア表現とは何でしょうか。私の理解した範囲で,すごーく簡単に(雑に?)説明しましょう。
この記事の最後に「関連動画&スライド」としてまとめていますので,必要に応じてみてください。
代数体 があります。
上のすべての有限次分離拡大を考えて,それらをすべて含むような分離拡大のことを分離閉包
といいます*1。絶対ガロア群
とは,
のガロア群のことで,
上のガロア群をすべて含んだガロア群の親玉みたいな存在です。
のことを詳しく知ることができれば,
上のすべての有限次拡大の情報がガロア対応を通して得られるので,
のことが知りたいという気持ちになります。
のことを知るために,表現論を使おうというのがガロア表現のアイデアです。
が「作用する」
係数のベクトル空間
を考えて,
への作用を通して得られる線形表現
を通じて
のことを知ろうと考えます。
つまり,
という連続な準同型写像を考えることになります。この をガロア表現といいます。
連続性を考えるということは,当然 や
に適切な位相が入っている必要があるわけですが,
にはクルル位相が,
には
に入る位相が誘導する位相が入ります。詳しくは [1] や [2] を参考に。
より一般に, の部分群
による商
を考えて,
を考えることもあります。この場合の もガロア表現と呼ぶことにします。
なお, はベクトル空間の自己同型のなす群なので,
の基底を固定すれば行列の群
と同型になります。したがって,
によって
を
という行列に移すことができるということですね。
行列なので,たとえばトレースや行列式が計算できます。これらをそれぞれ
と表すことにします。これらは基底の取り方によらない不変量になります。
また,ガロア表現 に対して,
の半単純化
という新たなガロア表現が作れます。詳しい定義は [2] の定義2-2-5で。
この半単純化に対しては,トレースの不変性
が成り立ちます。
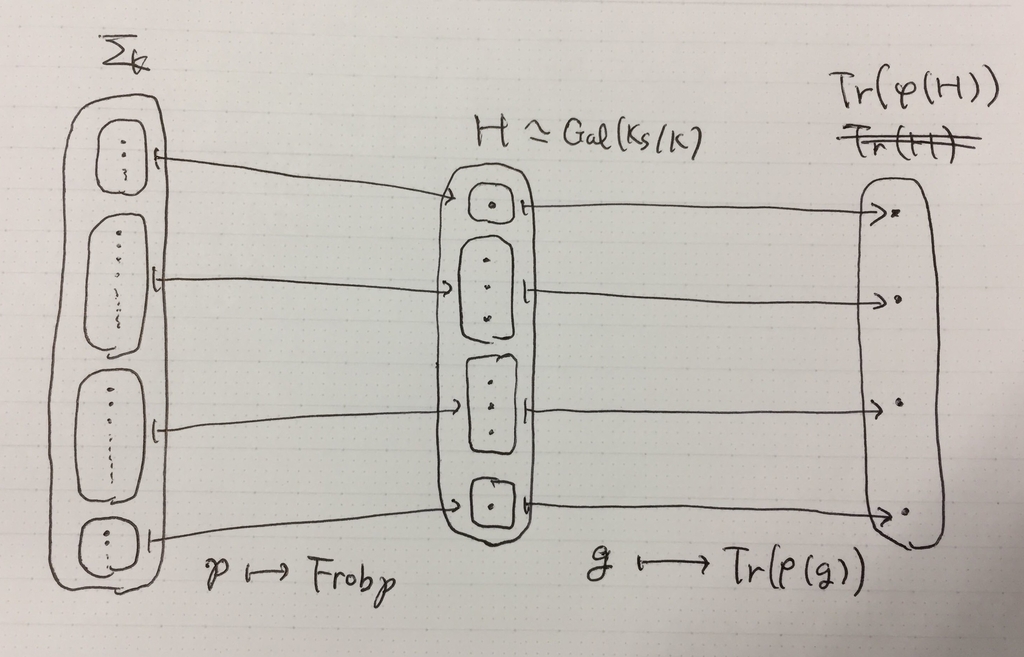
もう一つ,Chebotarevの密度定理にはフロベニウスという登場人物が必要ですので,その説明を簡単にします。
この記事を通して を
の素イデアル全体の集合とします。また,
を
の部分集合であるような有限集合とします。
に含まれない
の各素イデアルで不分岐な
の代数拡大(
の外不分岐な拡大と言います)で最大のものを考えて,それを
と表すことにします。この
のガロア群
の中にフロベニウス(自己同型)という重要な元がいます。
に対して
の元
が(共役を除いて)一意的に定まり,これを
についてのフロベニウス(自己同型)といいます。この
を
に持ち上げたものも同じく
と表現することにします。
また, の外不分岐な有限次拡大
に対しても,同様にフロベニウス
が定義できます。上の
(
の自己同型)を
に制限させたものは,
の自己同型となり,これは
のフロベニウスに一致します。そこで,
のフロベニウスも単に
と書くことにします。
また,ガロア表現にも分岐・不分岐という概念は定義されます。 についての惰性群
に対して,
が成り立つとき,
は
で不分岐であるといいます。そうではないとき,
は
で分岐するといいます。
なお, が分岐するような素イデアルの集合
は,
という
の拡大体を考えたときに,
で分岐する素イデアルとちょうど一致します。
2.ガロア表現(の半単純化)の同値性
一般に,2つのガロア表現 があったときに,両者が同値であるとは,任意の
に対して
が存在して
が成立するときをいいます。このとき, と
は同値であるといい,
と表します。
さて,一般に2つのガロア表現 があったときに,それらの同値性を示すのはなかなか難しい問題だと言われます。
ところがです。ガロア表現の半単純化については,次の定理によって同値性が判定できます。この定理が,本記事の本題です。
が成り立つならば, が成り立つ.
ガロア表現の半単純化については「(不分岐な についての)フロベニウスに対応するトレースの値」だけを見れば同値性が判定できるということを主張しています。言い換えると,ガロア表現の半単純化はフロベニウスのトレースの値によって一意的に定まると言えます。
可換環論を用いると「半単純加群はトレースが一致すれば一致する」という命題が(大変ですが)示せるそうです。(参考文献 [2] の命題2-2-7および付録(5節))
この命題を認めると,上の定理を示すためには
を示す必要があります。この証明にChebotarevの密度定理が使えるのです。
3.Chebotarevの密度定理とは
簡単にChebotarevの密度定理 *2 について紹介します。
有限次ガロア拡大 のガロア群
を考えます。
に共役
という同値関係を次のように入れます。
を共役関係で割った共役類を考えて,
の属する共役類を
と表しましょう。このとき,
のある共役類
に対して
なる集合を考えます。つまり, が共役類
に一致するような素イデアル
全体の集合です。
の素イデアル全体
に対する
の密度
を考えましょう。これが共役類
と
の位数を用いてかけるというのがChebotarevの密度定理です。
ここで, を単に密度と言いましたが,正確にいえば解析的密度と呼ばれるものです。詳しくは参考文献 [3] の1.1節を。
具体例として を考えましょう(
で,
は1の原始
乗根)。この場合,
となります。ここで, なる素数を考えると,
に対応するフロベニウス
は,ガロア群側では
に対応します。よって,
なる
の素イデアル
全体の集合を
と書くことができます。
Chebotarevの密度定理より
となることから, は無限集合です。したがって,
型の素数(
は互いに素)は無数に存在します。
この意味で,Chebotarevの密度定理は,ディリクレの算術級数定理 の一般化になっています。
4.Chebotarevの密度定理の使い方(前半)
Chebotarevの密度定理を使えば,上の(仮定)から(帰結)が得られるというわけですが,さてどうやって使うのでしょうか。
をガロア表現とします。
は
の部分群となります。
によって固定される
の部分体を考えると,それは
で分岐する
上の拡大体となります。これを
と表します。
このとき,準同型定理より自然な射影 を考えると,
なる準同型 が存在します。
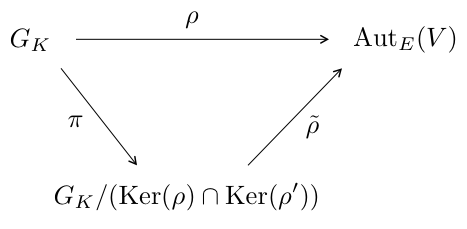
このようなとき,ガロア表現 は
を経由するといいます。
と置いておきましょう。
ガロア表現 は,
と比べて少し小さな群
を経由して,
の行き先によって決まるわけです(考えやすくなった)。したがって,
から定まるガロア表現
を考えれば十分だとわかります。
ここから,まず簡単な場合として,ガロア表現が の有限商を経由する場合(つまり
が有限の場合)を考えましょう。
もし, が有限群であれば(つまり,
が有限次拡大であれば),Chebotarevの密度定理を使ってただちに(帰結)が得られることがわかるでしょう。*3
というのも, ですが,
の任意の共役類
を考えると,Chebotarevの密度定理から
より,任意の共役類 に対してフロベニウスが存在する(素イデアル
が存在して
)ことがわかります。
また,ガロア表現のトレースの値は共役類に対して定まります。よって,任意のフロベニウスのトレースが決まれば,ガロア群の任意の元のトレースが決まるというわけです。
よって, が無限群になる場合,すなわち,
が有限とは限らない群を経由する場合について考える必要があります。
この場合は,Chebotarevの密度定理は直接的には使えませんが,Chebotarevの密度定理から従う次の系を使うことができます。
を共役で安定な
の部分集合で, 任意の
に対して
は
を含んでいるようなものとする.このとき
は
の稠密な部分集合となる.
証明は,参考文献 [3] の系1.4に書いてあります。
要するに上で言っていることは,不分岐な素イデアルについてのフロベニウスによってできる の部分集合
が
に稠密に入っているということです。
ガロア表現が有限群 を経由する場合は,
の任意の共役類すべてにフロベニウスがいてくれたので,ただちに証明できました。無限群
を経由する場合は,すべての共役類にフロベニウスがいるとはもはや言えません。一方で,フロベニウスに対応する
の部分群が
の中で稠密な部分集合になっていることは言えます。
これを使うとどのように(仮定)(帰結) を示していけるのでしょうか。
5.Chebotarevの密度定理の使い方(後半)
それでは, が有限群とは限らない場合について示していきましょう。
先に説明した通り, とすると,ガロア表現
は
を経由します。したがって,準同型定理より
を考えれば十分です。これらを改めて
とします。
ここで, の部分集合
を考えます。この が
に一致することが示すべき【帰結】です。
このとき, は
の閉集合であることがわかります。理由は [2] の脚注8にて。
一方, の部分集合
を考えます。つまり, は
の不分岐な素イデアルについてのフロベニウスに一致する
の元の集合です。
これは【仮定】により, に含まれます。なぜなら,【仮定】により少なくともフロベニウスについてだけいえば,
のトレースが一致することがわかっているからです。よって
です。
結果的に なる包含の列が得られました。
に対応する代数体
は,
としたときの
の外不分岐な最大のガロア拡大体
なので,
にChebotarevの密度定理の系が適用できて,
は
に稠密に入っていることがわかります。
稠密性の定義から, の閉包(定義:
を含むような最小の閉集合)は全体集合
に一致します。
したがって,閉集合 は
を含むので,明らかに
に一致しなければなりません。よって,
がいえるというわけです。
以上より,すべての について
と
のトレースが一致することがいえて,【帰結】が示されました。
証明おしまいです!
6.証明のキーポイントのおさらい
Chebotarevの密度定理の系は,フロベニウスの集合の稠密性に関するものでした。そのため,証明では位相的な議論が中心になりました。
まず, という
の部分集合の列を考えました。示したいことは
です。
また, が開集合,
が閉集合であることがわかっています。つまり,
は開集合
を含むような閉集合ということですね。
Chebotarevの密度定理から が稠密な部分集合であることが言えます。ここがポイントです。
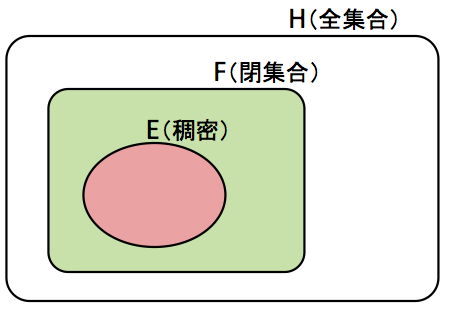
また,開集合を含むような最小の閉集合のことを閉包といいます。稠密性の定義から,稠密な開集合の閉包は全集合に一致します。
ここで は,
の開部分集合
の閉包を含むはずなので,
の稠密性から
は
に一致しなければなりません。
これで が言えてしまうのです!
面白いでしょう!
なお, が有限群のときは,Chebotarevの密度定理より,
が直接
に一致することが言えてしまいます。
したがって,明らかに となるわけです。
最後に感想を少々。
冒頭で述べた通り,「ガロア表現の同値性」と「Chebotarevの密度定理」の関係が理解できたのが嬉しかったというのが,この証明が好きな理由です。やっぱり自分の力で理解できたものは嬉しいし,愛着もわきますよね。
また,証明の技法としても面白いなと思いました。特に,位相空間の議論(稠密集合の閉包は全体に一致する)がここまできれいにハマるのは気持ちいいと感じました。
私は整数論を趣味で勉強していて,関係ないものはできれば勉強したくないと,これまで位相の勉強を避けてきたのです。今回,整数論の分野でまともに位相を使った議論をして,こうした基礎の必要性を強く感じました。
そういった意味でも私の固定観念を変えてくれた証明でした。
だいぶ長かったですが,これで終わりにしたいと思います。
それでは今日はこの辺で。
*1: は代数体なので,分離閉包ではなく代数的閉包としてもよいところかと思います(代数体は完全体であり,完全体の分離閉包は代数的閉包に一致するため)。今回は代数体しか扱いませんが,一応
が代数体でない場合も考慮して,ここでは参考文献にならって分離閉包としています。
*2:ところで,気になる人も多いと思うのでChebotarevという人の読み方を。「チェボタレフ」とか「チェボタリョーフ」といった読み方をみかけます。私は前者の読み方をしています。
*3:ちなみに,自明かのように書いていますが,これに私が気づいたのは一昨日の夜です。「Chebotarevの密度定理ってなぜ使えるんだろう」とずっと考えながらお風呂に入っているときに気づきました。