これまでtsujimotterのノートブックでは、循環小数についていろいろな話題を紹介してきました。今日はとっておきのトピックとしてアルティン予想 という 未解決問題 について紹介したいと思います。
このブログでは、これまでずっと 「素数 の逆数
の循環節の長さ」 について興味を持ってきました。
まずは、 なる素数
について、
の循環小数を計算してみましょう。例として
以下のものを計算してみます:
(長さ: 1)
(長さ: 6)
(長さ: 2)
(長さ: 6)
(長さ: 16)
(長さ: 18)
(長さ: 22)
(長さ: 28)
太字で書いたのは、循環節の長さがちょうど になっているものです。
実は、あとで述べるように、 の循環節の長さの限界は
になります。
そこで、長さがちょうど となる素数はいったいどの程度あるのか?という問題が気になってきます。
今回の主役であるアルティンは、このような長い循環節を持つ素数は、無限に多く存在し、その割合も具体的に計算できると予想しました。
これが成り立つとすれば大変興味深いですが、実際長い循環節を持つ素数については分かっていないことが多く、このアルティン予想は難問の一つとされています。
今日の記事では、まずアルティン予想の正確な主張を述べたいと思います。その上で、アルティン予想がいったいどういう理屈で予想できるのか、ヒューリスティックな議論を紹介したいと思います。この議論は代数的整数論・解析的整数論を使った大変面白い議論となっています。
最終的には、「あの有名な未解決問題」も登場します。最後までぜひご覧になってください!
0. 目次
1. 循環小数とmod pの原始根
まずは、循環小数についておさらいするところから始めましょう。
循環小数の循環節の長さは、長いものもあれば短いものもあります。一般に正整数 について、
の循環節の長さは
以下となります。さらに
という法則があるので、長い循環節を持つものを考えたければ素数の逆数を考えれば良いことになります。
一方で、 が素数ならば
の循環節の長さが
になるわけではないという点が面白いポイントです。素数であっても、長いものもあれば、短いものもあります。すると、循環節の長さが
になるものは一体どのような素数なのかということが気になりますね。
実際、上に挙げたうち5つの素数については循環節の長さが となっています。
(長さ: 6)
(長さ: 16)
(長さ: 18)
(長さ: 22)
(長さ: 28)
循環節の長さが の素数をわかりやすい性質によって特徴づけるのはなかなかに難しい問題です。それは、この問題が 原始根 に関係しているからです。
そもそも が循環するということは、
を
で順に割っていったときに、あまりがちょうど
になる
が存在することを意味します。
つまり、次が成り立ちます:
右辺の条件は「 における
の位数」を表します。
一般の で割り切れない整数
について、フェルマーの小定理により
が成り立ちます。よって、 の位数は
の約数となります。
そこで、位数が に一致する特別な
のことを
の原始根と言います。
以上をまとめるとこうなります:
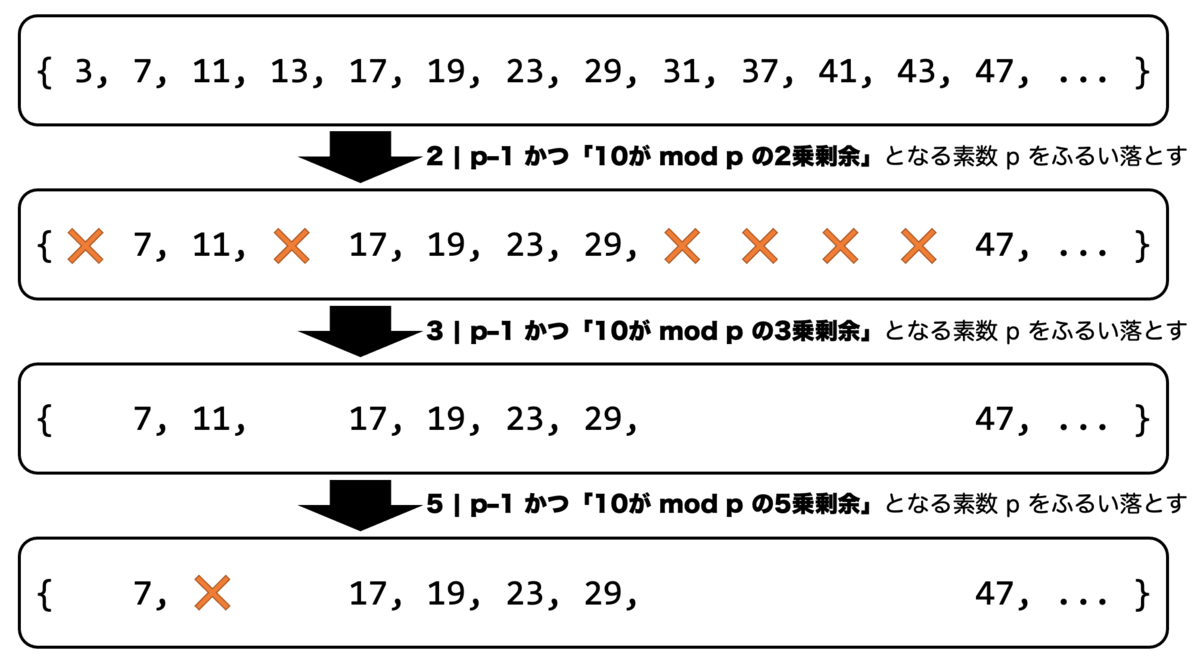
今回の場合、「 が
の原始根であるような素数
」を考えたいというわけですね。原始根を固定して素数を動かすイメージです(下図)。
が原始根であるような素数全体の集合を
と呼ぶことにしましょう。

はいったいどのような集合なのでしょうか?
の素数を何かわかりやすい条件で特徴付けることはできるでしょうか? そもそも
は無限集合でしょうか?
2. アルティン予想とは
そこでアルティン予想の登場です。簡単に言えば、アルティンは は無限集合であり、さらに素数全体に対する「密度」は 37% 程度だ と予想したのです。
この「密度」というのが少し難しい概念なので、補足します。
素数全体の集合を とすると、
は無限集合なので、もし
が無限集合だったとすると、その割合は
となってしまい、素朴には定義できません。
そこでどう考えるか。 未満の素数全体の集合を
として、
以下の
の元全体を
とします。ここで、
も
もどちらも有限集合ですので、割合を考えることができます。この割合に対して
の極限をとるわけです。
これを の(
における)密度と定義するわけですね。
密度を使ってアルティンの予想をより正確にいうと、次のような主張になります。
(i) 素数全体における の密度は正。特に
は無限集合。
(ii) とすると、素数全体における
の密度は
に依存しない定数
で表せて、
は次のように表せる:
を一般的な条件で考えているために主張が少しわかりづらくなっています。今回の問題では
の場合が重要だと考えて、このケースに限定すると次のような主張になります:
(i) 素数全体における の密度は正。特に
は無限集合。
(ii) 素数全体における の密度は、以下の定数
に一致する:
この を アルティン定数 といいます。実際、計算してみると
となります。だいたい ぐらいの定数となりますね。ここから、密度が37%だという話が出てきたというわけです。
実際、 以下の素数
で「
が
の原始根」である
全体
を計算してみたのが次の表です。
| x | |||
|---|---|---|---|
| 200 | 46 | 17 | 0.3695... |
| 400 | 78 | 29 | 0.3717... |
| 600 | 109 | 41 | 0.3761... |
| 800 | 139 | 48 | 0.3453... |
| 1000 | 168 | 60 | 0.3571... |
| 1200 | 196 | 75 | 0.3826... |
| 1400 | 222 | 86 | 0.3873... |
| 1600 | 251 | 98 | 0.3904... |
| 1800 | 278 | 108 | 0.3884... |
| 2000 | 303 | 116 | 0.3828... |
一番右の列 をグラフ化するとこうなります。青い線が
であり、オレンジ色の線がアルティン定数
です。
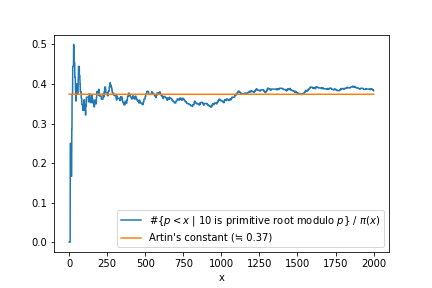
グラフを見る限りでは、 を大きくしていけばアルティン定数
(オレンジ色の線)に収束していってもおかしくない気はしますね。
もちろん、原始根については分かっていないことが多いですから、アルティン予想が外れてしまって、ある数以上の素数 について突然
を原始根に持たなくなる、という可能性もあります。
つまり、 がどんどん減少していって、極限が
になってしまうということもありえるわけですね。
アルティン予想は2021年現在証明されておらず、未解決問題です。いくらグラフの傾向からこのまま に収束しそうだと思えたとしても、そのことを証明しない限り数学的に正しい事実とは言えないわけですね。
もう一つは「アルティンのL関数が解析接続できるか」という問題で、今回のものとは直接関係はありません(たぶん)。調べる際はご注意を。
3. 原始根を言い換える
アルティン予想は「10を原始根に持つ素数」についての予想でした。
しかしながら、この原始根という条件は掴みづらく、この先どのようにして議論を進めたらよいか見当もつきません。そこで、もう少し別の見方ができないか考えてみましょう。
実は「原始根である」(というよりむしろ「原始根ではない」)という条件は、次のように書き直すことができます。以下、 や
と書いたら素数を表すこととし、このことを省略する場合があります。
は
の原始根ではない
ある素数
が存在して「①
」かつ「②
が解をもつ」
②の条件は 「 が
の
乗剰余」 とも言い換えられますね。
つまり「 を割るすべての素数
について、
が
の
乗剰余にならない」というのが「
が
の原始根」であるための必要十分条件、というわけです。
これを証明するために、以下の補題を証明します。
が解をもつ
(
このとき、仮定より である。
の位数は
より
よって、整数 を用いて
と表すと
と表せる。したがって
であり、 として
は解をもつ。
()
より、両辺
乗して(
なので
は整数であることに注意)
ゆえに、 が得られた。最後の
はフェルマーの小定理より。
この補題を使って、命題1を示します。
(
が成り立つ。このとき、 より
なので
を割り切る素数
が存在する。このとき、
であるから、
を満たす(①)。
ここである整数 を用いて
とおくと
となる。
ゆえに の両辺を
乗すると
であり、よって
が得られる。補題2より、 が解をもつ(②)が従う。
()
逆に補題2より、
なので、
として
がしたがう。これは
が原始根ではないことを意味する。
命題1によって「 乗剰余にならない」という条件を使って、原始根が特徴付けられることがわかりました。
を(やはり)素数全体の集合とし、
の部分集合
を
で定義します。(アルティン予想のときに定義したものと同じものです。)
知りたいことは、次のことでした:
命題1の性質を使って は次のように表せます。
最初に なる例外的な素数を除いておく必要がありますが、以降は
かつ
が
の
乗剰余となる素数
をふるい落としていけば、目的の集合が得られるということですね。
4. 素イデアルの分解法則に帰着
そんなわけで、命題1に出てきた条件
かつ
②
を考えてみましょう。
これを言い換えるために、なんと 代数的整数論 が使えるのです。
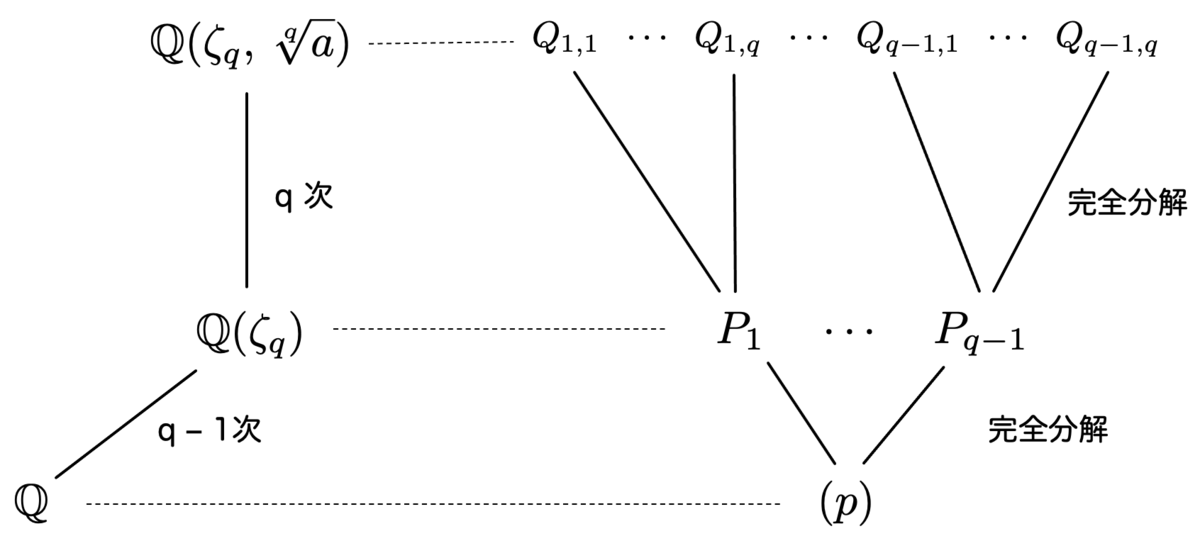
以下、 をsquare-free(平方因子を持たない)とします。
を1の原始
乗根とすると
という拡大は 次の円分拡大となります。
さらに、その上に を添加して
なる拡大を考えます。この拡大の拡大次数は 次となり、これを クンマー拡大 と言います。
拡大の様子を図に表すと、このようになります:

クンマー拡大とは、元々、任意の位数の巡回群をガロア群に持つ拡大(巡回拡大)を考える中で生まれた拡大です。 は
次の巡回拡大となります。
一般に、1の 乗根全体を含む体
の上の巡回拡大
は
にある
乗根を添加することで得られるというのがクンマー理論でした。
さて、ここで考えたいのは、クンマー拡大における 素イデアルの分解法則 です。
簡単な例を思い出すと、4で割って1あまる素数 は、
という拡大で分解されます。たとえば
のような感じです。これは素イデアルの等式
と思うこともできます。
一般に、 という代数体の拡大があったときに、
の整数環の素イデアル
を
の整数環のイデアルに持ち上げると
のように分解されます。このときの分解の個数 は「
公式」という有名な公式によって、拡大次数
の約数となります。
がちょうど
に一致するとき「素イデアル
は
で完全分解する」といいます。
類体論によれば、 のガロア群がアーベル群であれば、完全分解する素イデアルの法則を分かりやすく表すことができます。当然、巡回拡大であるクンマー拡大も同様です。
実際、素数 について、
を
に持ち上げたときの分解法則は、次のように表されるそうです:
なんと、先ほどの原始根にならない条件①②がそのまま出てくるのです。面白いですね!
完全分解する法則が上記のようになることについて、実は私自身は証明したわけではありません。今回は参考文献 [2], [3] の内容を認めて使いたいと思います。いつかちゃんと理解したいです。
で完全分解するためには、途中の円分拡大
で完全分解した上で、分解された素イデアルがさらに
で完全分解することが必要十分条件です。
① の条件は円分拡大
における完全分解の条件となっていますので、②の方はクンマー拡大での条件を反映したものと思われます。
5. アルティン予想を裏付ける「ヒューリスティックな」議論
準備が整ってきましたので、そろそろアルティン予想が成り立ちそうだと思える根拠を示していきたいと思います。
ただし、この節の議論はあくまで「ヒューリスティックな」議論です。ヒューリスティックとは
必ずしも正しい答えを導けるとは限らないが、ある程度のレベルで正解に近い解を得ることができる
もののことで、数学においては「厳密な証明ではないが予想をある程度裏付ける根拠」として用いられます。
したがって、以下の議論には正しくない議論が含まれます。予想の証明にはなっていませんし、ここから予想の証明に直接結びつくものでもありません。その点はご容赦ください。
そもそも冒頭に書いた通り、今回の記事の内容はいくらか乱暴な議論が含まれていますので、それを念頭に入れた上で読んでいただければと思います。
さて、前節のように問題を置き換えると、色々な道具が使えそうだと気づきます。
我々が知りたいのは、素数の密度でした。そこで、チェボタレフの密度定理(主張は適当にググってください)が使えないか考えてみます。
実際、次のことが言えます:
左辺は正確に言えば「解析的密度」と呼ばれるものです。
最初に定義した密度は「自然密度」と呼ばれるもので、自然密度が存在すれば「自然密度=解析的密度」であることが示されるそうなので、ここは気にしないでおきます。
左辺は素イデアルの分解法則より「① かつ ②
が解をもつ(
乗剰余)」となる素数
の密度と言い換えられます。
また、拡大次数は なので、右辺が
であることが示されます。
このことは、およそ次のようなことを言っています:
しかし、それを忘れて議論を進めます。
ここで、 以下の整数の中から素数の割合を「おおざっぱに」見積もるときの方法を思い出します。
以下の整数を1個取り出したとき、それが
の倍数ではない確率はだいたい
と表せます。また、 の倍数ではない確率はだいたい
であり、 の倍数ではない確率はだいたい
と表せます。
したがって、 を
以下の最大の素数として
が、 以下の数が素数になるような確率と言えそうです。(もちろん、この議論は厳密ではありません。)
同様のことを についても考えます。
以下の素数
を1個取り出します。このとき、
が素数
について「①
かつ ②
は
の
乗剰余」を満たさない確率は、密度定理によればだいたい
と表せそうです。
したがって、「 乗剰余でふるい落とす」ことを考えると、
の密度は
と表せそうです。最後に得られた無限積がまさにアルティン定数というわけですね!
素数の個数のときと同様に、実際には "" のニアリーイコールは厳密な議論ではありません(間違いその2)。あくまでヒューリスティックな議論というわけですね。
とはいえ、計算結果にちゃんとアルティン定数が出てきました。これは嬉しいですね!
アルティン予想が成り立っていそうな根拠を示す程度の議論はできたのではないかと思います。
6. 拡張されたリーマン予想との関係
面白いことに、アルティン予想はある意味では定理 *1 です。
どういうことかというと、ある有名な未解決問題を仮定すれば、アルティン予想を示すことができるそうなのです。その予想とは 拡張されたリーマン予想(ERH) です。
実際、1967年にChristopher Hooleyによって、次の定理が示されています:
素数定理を証明するためには、リーマン・ゼータ関数 において「零点が存在する領域」の評価が必要でした。
アルティン予想も、ある意味で原始根に関する素数定理だと思うことができます。デデキント・ゼータ関数におけるリーマン予想の類似
を拡張されたリーマン予想(ERH)というそうです。今回扱った拡大体 に対応するデデキント・ゼータ関数
について、ERHを仮定することでアルティン予想を示したのがHooleyの論文ということになります。
実際の証明については私にはまだ理解できる気がしませんが、いつかは理解したいと思っています。
ところで、ここまで「ERH」と記述してきましたが、文献 [2] においては「一般化されたリーマン予想(GRH)」の方を仮定すると書いています。
Wikipedia「一般化されたリーマン予想」によると、次のように両者は異なる予想として記述されています:
- (GRH)ディリクレのL関数について、リーマン予想の類似が成り立つ
- (ERH)デデキントのゼータ関数
について、リーマン予想の類似が成り立つ
実際、[1] のHooleyの論文を眺めてみると、デデキントのゼータ関数におけるリーマン予想を仮定しているようなので、仮定すべきはERHということになります。
ただ、Wikipediaにもあるように『なお多くの数学者は、一般化されたリーマン予想という名称をディリクレのL-函数に対する場合だけではなく、全ての大域的なL-函数に対する場合を一般的に示す名称として使っている。』とのことなので、GRHと書いても問題ないのかもしれません。(実際、[3] ではGRHと言っておきながら、デデキントゼータの方を紹介していました。)
いずれにしても、デデキント・ゼータ関数についてのリーマン予想を仮定することで、アルティン予想を証明できるというのが言いたかったことです。リーマン予想って、相変わらずすごいです。
循環小数は素朴な対象に見えるかもしれませんが、深く考えるとここまで到達するのかと、循環小数の深淵を覗いた気がします。まさか「循環小数」と「ゼータ関数」のタグが同じ記事で並ぶことになるとは思いもしませんでした。数学って本当に面白いなぁ。
それでは今日はこの辺で!
参考文献
[1] Christopher Hooley, "On Artin’s conjecture" (1967).
https://eudml.org/doc/150785
[2] 村田 玲音「剰余位数の分布について」(2012)
https://meigaku.repo.nii.ac.jp/?action=pages_view_main&active_action=repository_view_main_item_detail&item_id=220&item_no=1&page_id=13&block_id=21
[3] M. Ram Murty, "Artin’s Conjecture for Primitive Roots" (2005).
http://web.math.ucsb.edu/~agboola/teaching/2005/winter/old-115A/murty.pdf
ちなみに、アルティン予想の名は「博士の愛した数式」にも出てくるらしいですね。私は読んだことがないのでわかりませんが、知っている方いましたらぜひ教えてください。
*1:これは少し言い過ぎな表現ですが、「ERHを公理に付け加えれば定理」という程度の意味です。
