類体論の基本不等式の証明 - tsujimotterのノートブック

Zeta Advent Calendar 2020 の14日目の記事です。

先日、類体論の入門記事を公開しましたが、多くの方に読んでいただいて嬉しいです。
tsujimotter.hatenablog.com

類体論の記事を書いたことによって頭の中が整理されて、類体論の本が読めるようになってきました。これがとても嬉しく思っています。

そんな経緯で類体論の基本不等式を理解できたのですが、今回はこれについて紹介したいと思います。

f:id:tsujimotter:20201214161050p:plain:w300

実はこの基本不等式は類体論の理論の中で証明される非常に重要な定理なのですが、これが解析的に証明されるのです。その証明にはゼータ関数を使います。この事実が面白いので今回紹介したいと思いました。

前回の記事は入門記事でしたが、今回はだいぶ専門的な内容になります。難しい内容になるかと思いますが、よろしければ最後までお付き合いください。

基本不等式について

上の記事では類体と呼ばれる概念を定義していました。しかしながら、直感的な理解を優先し、通常のものとは異なる定義を採用していました。

今回の記事では「通常の類体の定義」を説明したいと思います。「基本不等式」とは、その通常の定義の中で導入される不等式のことです。

あえていうなら、

前回：足立「類体論へ到る道」の定義
今回：足立「類体論講義」の定義

ということになります。両者がどういう関係にあるかは後ほど触れたいと思います。

まず、有限次ガロア拡大 $L/K$ を考えます。この $L$ が類体であるとはどういうことかを定義したいと思います。

前回同様 $K$ の整イデアル $\newcommand{\mm}{\mathfrak{m}}\mm$ を考えます。

正確に言えば、無限素点も因子に含むので「整因子」ですが、細かいことは置いておきましょう。

$K$ の分数イデアル全体 $A_K$ および $L$ の分数イデアル全体 $A_L$ を考えます。これらのうち、特に $\mm$ と素なもの全体をそれぞれ $A_K(\mm), \; A_L(\mm)$ 表すことにしましょう。

分数イデアル $\mathfrak{a}$ を素イデアル分解したときの素因子に $\mm$ の素因子が含まれないとき、 $\mathfrak{a}$ は「 $\mm$ と素」であるといいます。

$A_K(\mm)$ のうち、特に単項分数イデアル $(\alpha)$ であって、その生成元 $\alpha \in K$ が

$\alpha \equiv 1 \pmod{\mm}$

を満たすようなもの全体を考えます。ここで、生成元 $\alpha \in K$ は符号を任意にとれるように思えるかもしれませんが、実は無限素点の合同式を満たすように符号を選んでいます。

このような単項分数イデアル全体を $S_K(\mm)$ と表すことにします。すなわち

$S_K({\mm}) = \{(\alpha) \mid \alpha \in K, \;\; \alpha \equiv 1 \pmod{\mm}\}$

です。ここで、 $S_K(\mm)$ を $\mm$ を法とするStrahl（シュトラール）、あるいはray（レイ）というそうです。

前回のray類体の名前はここから来ているみたいですね。Strahlがドイツ語で、rayが英語だそうです。ray類体のことをStrahl類体と呼ぶ本もあります。

さて、 $A_K(\mm)$ を部分群 $S_K(\mm)$ で割ってできた群が、「 $\bmod{\mm}$ の合同イデアル類群」で

$\newcommand{\cl}{\operatorname{Cl}}\cl_K(\mm) = A_K(\mm)/S_K(\mm)$

と表します。この定義は前回紹介していませんでした。

イデアル類群は、分数イデアル全体を単項分数イデアル全体で割ったものでした。上の合同イデアル類群は、さらにそれを $\bmod{\mm}$ で細かく分類したような構造をしています。

$\mm = (1)$ としたとき、両者はちょうど一致します。すなわち、合同イデアル類群はイデアル類群の一般化になっています。

前回は「 $\bmod{\mm}$ の合同イデアル類群」 $\cl_K(\mm) = A_K(\mm)/S_K(\mm)$ の部分群を考えて、それに属する素イデアルが分解する体を類体の定義としたのでした。

今回は、 $\cl_K(\mm)$ の部分群を考えるのではなく、 $S_K(\mm)$ を含むような $A_K(\mm)$ の部分群 $H(\mm)$ を考えます。すなわち

$S_K(\mm) \subset H(\mm) \subset A_K(\mm)$

を満たす $H(\mm)$ を考えるということですね。このような $H(\mm)$ を $\mm$ を法とする合同群といいます。この $H(\mm)$ に対応するような体を考えたいわけですね。

前回と今回扱う部分群は、似てはいますが微妙に異なっています。どのように対応づけられるのでしょうか。

実は、群論の一般論により「 $S_K(\mm)$ を含む $A_K(\mm)$ の部分群全体」と「 $A_K(\mm)/S_K(\mm)$ の部分群全体」の間には1対1対応があります。

そのため、今回のように「 $S_K(\mm)$ を含む $A_K(\mm)$ の部分群 $H(\mm)$ 」を考えても、前回とまったく同じような議論ができるというわけですね。

類体は前回よりも少しだけ遠回りして定義されます。まず、有限次ガロア拡大 $L/K$ において、 $\mm$ と素な $L$ の分数イデアル全体 $A_L(\mm)$ を考えて、これに対してノルム写像

$N_{L/K} \colon A_L \longrightarrow A_K$

を適用します。ノルム写像によって $L$ の分数イデアルが $K$ の分数イデアルになるわけです。

$\mm$ と素な $L$ の分数イデアルは、同様に $\mm$ と素な $K$ の分数イデアルに映るわけです。したがって、 $A_L(\mm)$ の像 $N_{L/K} A_L(\mm)$ は、 $A_K(\mm)$ の部分群です。

$N_{L/K} A_L(\mm)$ と $S_K(\mm)$ との積をとると（任意の元を掛け合わせる）、これは $S_K(\mm)$ を含む $A_K(\mm)$ の部分群となります。したがって

$H_{L/K}(\mm) = S_K(\mm) N_{L/K} A_L(\mm)$

とすると、これは $\mm$ を法とする合同群です。これは、 $L/K$ と $\mm$ に対して決まる群となっています。

ここで一旦想像して欲しいのですが（あくまで想像なのでこれそのものは成り立ちません）、

$\newcommand{\gal}{\operatorname{Gal}} \gal(L/K) \simeq A_K(\mm) / H_{L/K}(\mm)$

のような同型が成り立ってくれたらいいな、と思うわけです。特に、 $L/K$ の拡大次数と右辺の合同群の群指数が一致して欲しいと思うわけですね。

上記の等式は一般には成り立たないのですが、以下の不等式ならば一般の有限次ガロア拡大に対して成り立ちます：

定理（基本不等式）

任意の有限次ガロア拡大 $L/K$ および $K$ の任意の整因子 $\mm$ について、次の不等式が成り立つ：

$[ L : K ] \geq ( A_K(\mm) : H_{L/K}(\mm) )$

これが基本不等式です。合同群の指数より拡大次数の方が一般に大きくなるという意味の不等式ですね。

先ほど、 $H_{L/K}(\mm)$ は $L/K$ と $\mm$ に対して決まると言いました。 $L/K$ を固定して $\mm$ の方を動かしてみましょう。

$\mathfrak{m}$ を変えると（つまり、取る $\bmod{\mathfrak{m}}$ を変えると）、左辺は一定のままで右辺の群指数が変わることになります。左辺によって上限が与えられているので、右辺の群指数が最大になるような $\mathfrak{m}$ を取ることができますね。

ここで次のような定義が考えられます：

定義

基本不等式の右辺の群指数を最大にするような $\mathfrak{m}$ について、合同群 $H_{L/K}(\mm)$ はガロア拡大 $L/K$ に対応しているという。

$L/K$ に対応するような $H_{L/K}(\mm)$ は複数ありえます。そういう $\mm$ は複数とりうるというわけですね。

ここで、 $\mm_1, \mm_2$ が対応するものだとして、 $A_K(\mm_1)/H_{L/K}(\mm_1)$ と $A_K(\mm_2)/H_{L/K}(\mm_2)$ は同型になります。したがって、類体を考える上では、どっちの $\mm_1, \mm_2$ を考えても問題ないというになりますね。

ちなみに、このような $\mm$ に対して、適当に因子 $\mm_0$ をかけた $\mm_0 \mm$ を考えても、実は $H_{L/K}(\mm_0 \mm)$ は $L/K$ に対応します。
（これは、 $\bmod{4}$ を考えても、その5倍の $\bmod{20}$ を考えても本質的には法則が変わらないのに似ています。）

つまり、 $L/K$ に対応する整因子としては、いくらでもその素因子を増やすことができるわけですね。したがって、一番素因子の個数が少ない整因子が本質的になります。このような $\mm$ を $L/K$ の導手と呼ぶようです。（今回は使いませんが参考までに。）

類体の再定義

さて、ようやく類体の定義に入ることができます。すなわち、上記の基本不等式がちょうど等号になるような $L/K$ を類体というわけです。

定義（類体）

$H(\mm)$ を $K$ の整因子 $\mm$ を法とする合同群とする。（すなわち、 $S_K(\mm) \subset H(\mm) \subset A_K(\mm)$ 。）

ガロア拡大 $L/K$ に対して

$H(\mm) = S_K(\mm) N_{L/K} A_L(\mm)$

が成り立ち、さらに基本不等式における等号

$[ L : K ] = ( A_K(\mm) : H_{L/K}(\mm) )$

が成り立つとき、 $L/K$ は $H(\mm)$ の類体という。

これを使うと、類体論の主要な定理の主張を書くことができます。

定理（基本定理）

$H_{L/K}(\mm)$ をアーベル拡大 $L/K$ に対応する合同群とすると、基本不等式に等号が成立する。すなわち、アーベル拡大は類体である。

任意のアーベル拡大は、実は類体であったというわけですね。すなわち、アーベル拡大に対応する合同群が存在するということです。

逆に、合同群に着目したときに、類体を持つような合同群はどれぐらいあるでしょうか。実は、すべての合同群に対して、その類体が一意的に存在するというのが、次の存在定理です。

定理（存在定理）

任意の合同群 $H(\mm)$ に対して、その類体が一意的に存在する。

すなわち、 $S_K(\mm) \subset H(\mm) \subset A_K(\mm)$ なる $H(\mm)$ に対して

$H(\mm) = S_K(\mm) N_{L/K} A_L(\mm)$
$[L : K] = (A_K(\mm) : H(\mm))$

を満たすような有限次ガロア拡大 $L/K$ が一意的に存在する。（結果的には、これはアーベル拡大となる。）

基本定理により任意のアーベル拡大は類体であり、拡大次数（すなわちガロア群の位数）は合同群の指数に一致するのでした。実は、このとき単に次数が一致するだけでなく、群としての同型が成立するというのが、次の同型定理です。

定理（同型定理）

$L/K$ を $H(\mm)$ の類体とする。このとき、以下の同型が成り立つ：

$\gal(L/K) \simeq A_K(\mm)/H(\mm)$

すなわち、上の方で「成り立ってくれたらいいな」といった状況が、アーベル拡大なら成立するというわけですね。

さて、ここまで一切「素イデアルの分解法則」の話が出ていませんので、不安になった方もいるかもしれません。前回は、類体は素イデアル分解によって定義したはずなのに。

分解法則は、上の同型が教えてくれます。

まず、アルティン相互法則という定理があって、上の同型写像は

$\newcommand{\pp}{\mathfrak{p}}\begin{align} A_K(\mm)/H(\mm) &\xrightarrow{\;\simeq \;} \gal(L/K), \\ \pp H(\mm) &\longmapsto \sigma_{\pp }\end{align}$

という対応によって与えられます。

円分体のときにやったように、

フロベニウス $\sigma_{\pp }$ がガロア群の中で単位元 $\Longleftrightarrow$ $\pp$ は $L/K$ で完全分解する

が成り立つのでした。

したがって同型定理より「 $\sigma_{\pp }$ が単位元」という条件は「 $\pp \in H(\mm)$ 」という条件と同値です。結局、素イデアルが対応する合同群 $H(\mm)$ に属するかどうかで、素イデアル分解法則が定まるということです。

ゼータ関数の導入

さて、そんなわけで、類体論において基本不等式

$[L : K] \geq (A_K(\mm) : H_{L/K}(\mm))$

が果たす役割が理解できたかと思います。

ここからが本題なのですが、基本不等式の証明にチャレンジしてみましょう。

非常に面白いことに、基本不等式の証明にはゼータ関数が使われます。つまり、解析的な議論が用いられるのですね。

今回使うゼータ関数は次のものです。

ある合同群 $H(\mm)$ に対して、合同類群 $A_K(\mm)/H(\mm)$ を考えます。これは有限群になりますが、これを定義域とするような群の指標を考えます。すなわち

$\chi \colon A_K(\mm) / H(\mm) \longrightarrow \mathbb{C}^\times$

なる群の準同型写像を考えるわけですね。

上の指標は「 $\mm$ と素な $K$ の整イデアルに対して定義されている」と思うことができますが、 $\mm$ と素ではない $K$ の整イデアル $\mathfrak{a}$ に対しても $\chi(\mathfrak{a}) = 0$ とすることで、 $K$ のイデアル全体に対して定義することができます。

ディリクレ指標みたいな定義の仕方ですね。

このとき、ディリクレ級数

$\displaystyle L(s, \chi) = \sum_{\mathfrak{a}}\frac{\chi(\mathfrak{a})}{ (N_K(\mathfrak{a}) )^s}$

を考えます。 $\mathfrak{a}$ は $K$ の整イデアル全体を渡ります。この級数は $\mathrm{Re}(s) > 1$ において絶対収束し、その範囲で解析関数を表します。これが今回考えるゼータ関数（L関数）です。

このゼータ関数は次のようなオイラー積を持ちます。

$\displaystyle L(s, \chi) = \prod_{\pp } \left( 1 - \frac{\chi(\pp )}{(N_K(\pp ))^s}\right)^{-1}$

$\pp$ は $K$ の 0 でない素イデアル全体を渡ります。

指標が単位指標 $\chi = \chi_1$ の場合は

$\displaystyle L(s, \chi_1) = \prod_{(\pp , \mathfrak{m}) = 1} \left( 1 - \frac{1}{(N_K(\pp ))^s}\right)^{-1}$

となり、 $\mathfrak{m}$ を割る（有限個の）素イデアルに関するオイラー因子を除いて、デデキント・ゼータ関数と一致します。

ここで、上のゼータ関数の解析的な性質について述べておきます。

定理

$L(s, \chi)$ は複素平面全体に解析的に延長され、 $\chi$ に応じて次のような性質を持つ：

$\chi \neq \chi_1$ ならば $L(s, \chi)$ は整関数（複素平面全体で正則）である。
$\chi = \chi_1$ ならば $L(s, \chi)$ は有理型関数で $s = 1$ において1位の極をもち、これが唯一の極である。

※実際に今回の証明で必要なものよりも、一般的な定理を書いています。

さて、 $L(s, \chi)$ のオイラー積に対して $\log$ をとると

$\displaystyle \log L(s, \chi) = - \sum_{\pp } \log \left( 1 - \frac{\chi(\pp )}{(N_K(\pp ))^s}\right)$

となります。テイラー展開 $-\log(1-x) = x + \frac{1}{2}x^2 + \frac{1}{3}x^3 + \cdots$ より

$\displaystyle \begin{align} \log L(s, \chi) &= - \sum_{\pp } \log \left( 1 - \frac{\chi(\pp )}{(N_K(\pp ))^s}\right) \\ &= \sum_{\pp } \frac{\chi(\pp )}{(N_{K}\pp )^s} + \frac{1}{2} \sum_{\pp } \frac{\chi(\pp )^2}{(N_{K}\pp )^{2s}} + \cdots \end{align}$

となります。

ここで、第2項以降について、たとえば第2項は

$\displaystyle \sum_{\pp } \left|\frac{\chi(\pp )^2}{(N_{K}\pp )^{2s}}\right| < \sum_{\mathfrak{a}} \left|\frac{\chi(\mathfrak{a})^2}{(N_{K}\mathfrak{a})^{2s}}\right|$

となり、右辺は $L(s, \chi)$ の定義級数に対して、 $2s, \chi^2$ を代入して得られる級数（に絶対値をつけたもの）なので、 $\operatorname{Re}(s) > \frac{1}{2}$ において収束します。すなわち、 $s = 1$ において正則です。

また、第1項についても正則な部分とそうでない部分に分けます。 $N_K \pp = p^f$ と書いたときに $f$ を $\pp$ の次数といいます。第1項の和 $\sum_{\pp }$ を次数1と次数2以降のものに分けたときに、次数2以降の和は $s = 1$ において正則です。たとえば次数2の素数を $\pp _2$ と表したとき

$\displaystyle \sum_{\pp _2} \frac{\chi(\pp _2)}{(N_K \pp _2)^s} = \sum_{\pp _2} \frac{\chi(\pp _2)}{p^{2s}}$

となり、たしかに右辺は $s = 1$ で正則ですね。

そこで、次数 1 の素数 $\pp_1$ に関する和を

$\displaystyle \sum_{\pp_1} \frac{\chi(\pp_1)}{(N_K \pp_1)^s}$

とします。すると、 $\log L(s, \chi) - \sum_{\pp_1} \frac{\chi(\pp_1)}{(N_K \pp_1)^s}$ は $s = 1$ で正則な関数となります。

このことを

$\displaystyle \log L(s, \chi) \sim \sum_{\pp_1} \frac{\chi(\pp_1)}{(N_K \pp_1)^s}$

のように表すことにしましょう。実際、差が $s = 1$ で正則であるような関数を $\sim$ で結ぶ関係は同値関係になりますね。

特に $\chi = \chi_1$ （単位指標）の場合は、 $L(s, \chi_1)$ は $s = 1$ において1位の極を持つので

$\displaystyle \log L(s, \chi_1) \sim \sum_{\pp_1} \frac{1}{(N_K \pp_1)^s} \sim \log\frac{1}{s-1}$

が成り立つことになります。

指標を考えるときは、すべての指標について和をとって考えるのが定石の一つです。一般に、有限群 $G$ とその任意の元 $g$ に対して、 $G$ 上の任意の指標 $\chi$ に対する和は、次のように計算できます：

$\displaystyle \sum_{\chi} \chi(g) = \begin{cases} \# G & (g = e) \\ 0 & (g\neq e) \end{cases}$

これを指標の直交性と言います。

直交性の式を $G = A_K(\mathfrak{m})/H(\mathfrak{m})$ 上の指標に対して適用すると

$\displaystyle \sum_{\chi} \chi(\pp_1) = \begin{cases} h & (\pp_1 \in H(\mathfrak{m}) ) \\ 0 & (\pp_1 \not\in H(\mathfrak{m}) ) \end{cases}$

となります。ここで、 $h = (A_K(\mathfrak{m}) : H(\mathfrak{m}) )$ と定義しています。

したがって、 $\log(s, \chi)$ を任意の $\chi$ で和をとれば

$\displaystyle \sum_{\chi}\log L(s, \chi) \sim \sum_{\pp_1} \sum_{\chi} \frac{\chi(\pp_1)}{(N_K \pp_1)^s} \tag{*}$

となります。

式 $(*)$ の右辺については、指標の直交性により

$\displaystyle h\sum_{\pp_1 \in H(\mathfrak{m})} \frac{1}{(N_K \pp_1)^s}$

が成り立つというわけですね。

式 $(*)$ の左辺についてなのですが、もしここで

$\displaystyle \chi \neq \chi_1 \; \Longrightarrow \; L(1, \chi) \neq 0$

であると仮定してみましょう。

これが成り立つならば、 $\chi \neq \chi_1$ ならば $\log L(s, \chi)$ は $s = 1$ で正則です。したがって

$\displaystyle \sum_{\chi} \log L(s, \chi) \sim \log L(s, \chi_1) \sim \log \frac{1}{s - 1}$

となります。

結局、式 $(*)$ の右辺と左辺の計算結果を結ぶと

$\displaystyle h\sum_{\pp_1 \in H(\mathfrak{m})} \frac{1}{(N_K \pp_1)^s} \sim \log \frac{1}{s - 1}$

が成り立ちます。

よって、 $s$ を $s > 1$ なる実数とすると

$\displaystyle \lim_{s \to 1} \sum_{\pp_1 \in H(\mathfrak{m})} \frac{1}{(N_K \pp_1)^s} \bigg/ \frac{1}{s - 1} = \frac{1}{h} \tag{**}$

が成り立ちます。

基本不等式の証明

ここまでは、 $K$ だけの議論でした。ここからは、 $L/K$ を $n$ 次ガロア拡大とし、 $L$ に対して同様の級数を考えます。すなわち、 $L$ の次数が 1 の素イデアルを $\mathfrak{P}_1$ と表すことにすると、 $K$ のときと同様に

$\displaystyle \sum_{\mathfrak{P}_1} \frac{1}{(N_L \mathfrak{P}_1)^s} \sim \log\frac{1}{s-1}$

となります。

ここで、上の和は $L$ の次数が 1 の素イデアル全体の和を渡るわけですが、 $\mathfrak{P}_1$ としては、次のいずれかとなります：

$\mathbb{Q}$ 上の素数が $L/\mathbb{Q}$ で $[L : \mathbb{Q}]$ 個の素イデアルに分解（完全分解）してできた一つの素イデアル
$\mathbb{Q}$ 上の素数が $L/\mathbb{Q}$ で分岐してできた素イデアル

このうち、下の方の素イデアルは高々有限個ですから、 $s = 1$ での正則性を考える上では除いてしまっても問題ありません。すなわち、 $\mathfrak{P}_1$ としては上側の素イデアルに限定しても問題ありません。

$L/\mathbb{Q}$ で完全分解するということは、 $K/\mathbb{Q}$ で完全分解し、さらに $L/K$ で完全分解するということです。したがって、 $\mathfrak{P}_1$ は $L/K$ で完全分解する $K$ の素イデアル $\mathfrak{p}_1$ の素因子となります。

すなわち、このような $\mathfrak{p}_1$ 1個に対して、 $L$ の素イデアル $\mathfrak{P}_1$ は $n = [L : K]$ 個対応することになります。

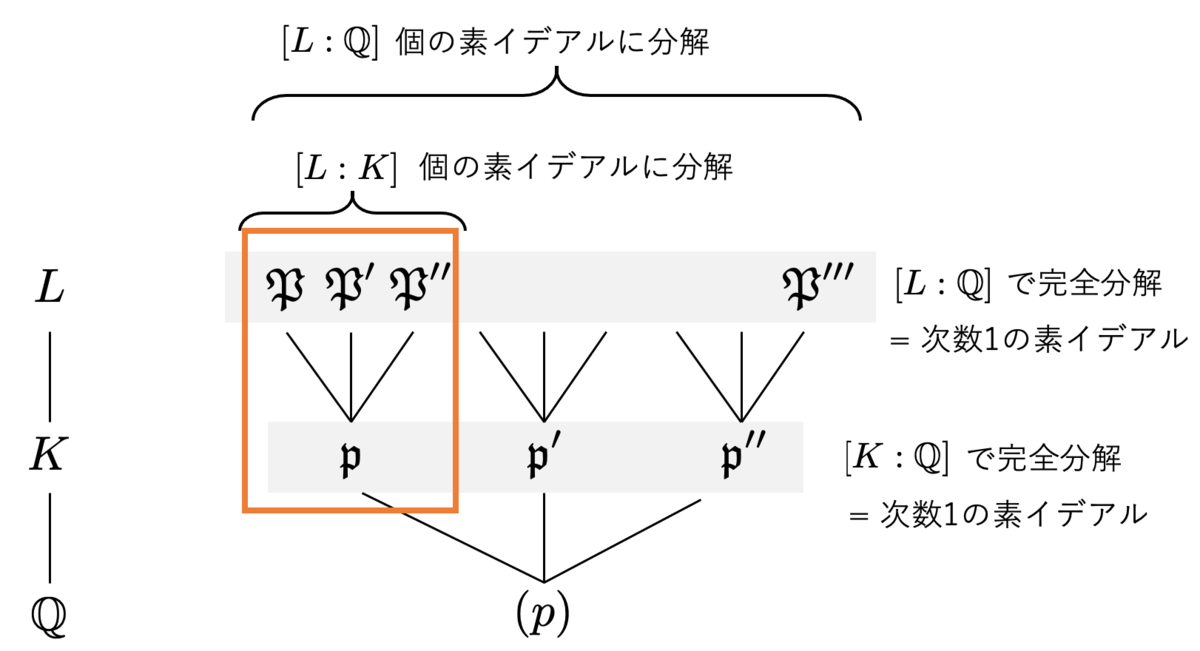
f:id:tsujimotter:20201212172047p:plain:w500

したがって、 $\pp_1^*$ によって「 $L/K$ で完全分解する $K$ の 1 次の素イデアル」を表すとすると、

$\displaystyle \sum_{\mathfrak{P}_1} \frac{1}{(N_L \mathfrak{P}_1)^s} \sim n \sum_{\mathfrak{p}_1^*} \frac{1}{(N_K \mathfrak{p}_1^*)^s} \sim \log\frac{1}{s-1}$

ということになります。 $n$ で割って

$\displaystyle \sum_{\mathfrak{p}_1^*} \frac{1}{(N_K \mathfrak{p}_1^*)^s} \sim \frac{1}{n}\log\frac{1}{s-1}$

となります。

ここで、 $H_{L/K}(\mathfrak{m}) = S_K(\mathfrak{m}) N_{L/K} A_L(\mathfrak{m})$ とします。先ほどの議論により $N_{L/K} \mathfrak{P}_1 = \mathfrak{p}_1^*$ なので、

$\mathfrak{p}_1^* \in N_{L/K} A_L(\mathfrak{m}) \subset H_{L/K}(\mathfrak{m})$

となります。

よって、 $s > 1$ を実数とすると

$\displaystyle \sum_{\mathfrak{p} \in H_{L/K}(\mathfrak{m})} \frac{1}{(N_K \pp)^s} \geq \sum_{\pp_1^*} \frac{1}{(N_K \pp_1^*)^s} \sim \frac{1}{n}\log \frac{1}{s-1}$

となります。

左辺を $\log \frac{1}{s-1}$ で割ったものの $s \to 1$ の極限をとると、式 $(**)$ により $\frac{1}{h}$ になるのでした。右辺も同様に極限をとると $\frac{1}{n}$ となります。したがって

$\displaystyle \frac{1}{h} \geq \frac{1}{n}$

すなわち、基本不等式

$\displaystyle [L : K] = n \geq h = (A_K(\mathfrak{m}) : H_{L/K}(\mathfrak{m}))$

が示されました。

あとは、四角で囲んだ部分だけが残されています。

$\displaystyle \chi \neq \chi_1 \; \Longrightarrow \; L(1, \chi) \neq 0 \tag{再掲}$

$\chi \neq \chi_1$ に対して、 $L(s, \chi)$ が $s = 1$ で $a_\chi$ （ $a_{\chi} \geq 0$ ）位の零点を持つとします。ここで、すべての $\chi$ に対して $a_\chi = 0$ が言えたら証明終了です。

このとき

$\displaystyle \begin{align} L(s, \chi) &= c_0 (s-1)^{a_{\chi}} + c_1 (s-1)^{a_{\chi+1}} + \cdots \\ &= c_0 (s-1)^{a_{\chi}} \left(1 + \frac{c_1}{c_0}(s-1) + \cdots \right) \end{align}$

のようにおくと、対数とって

$\displaystyle \begin{align} \log L(s, \chi) &= \log c_0 + \log (s-1)^{a_{\chi}} + \log \left(1 + \frac{c_1}{c_0}(s-1) + \cdots \right) \\ &\sim \log (s-1)^{a_{\chi}} = -a_{\chi} \log \frac{1}{s-1} \end{align}$

が成り立ちます。まとめると

$\displaystyle \log L(s, \chi) \sim -a_\chi \log \frac{1}{s-1}$

が成り立つということです。

すべての $\chi$ に対して足し合わせると

$\displaystyle \sum_{\chi} \log L(s, \chi) \sim \left(1 - \sum_{\chi} a_\chi\right) \log \frac{1}{s-1}$

が成り立ちます。

左辺はこれまでの議論で $s \to 1$ で正の無限大に発散することがわかっています。したがって、右辺もそうであるべきですが、このとき右辺の係数が $\left(1 - \sum_{\chi} a_\chi\right) > 0$ でなければなりません。ここから、 $a_\chi \geq 0$ の条件より、すべての $\chi$ に対して $a_\chi = 0$ であることが導かれます。