tsujimotterのノートブックでは,これまで2回にわたって,岩澤理論の3本柱のうちの2つ「岩澤類数公式」「p進L関数」を紹介してきました。
今日は,3本柱の最後1つである
について紹介したいと思います。
岩澤主予想は「予想」と呼ばれていますが,既に証明された定理です。したがって,本来は「定理」と呼ぶべきものですが,一般には「岩澤主予想」という呼び名で定着されていますので,本記事でもその呼び方でいきたいと思います。英語だと "Iwasawa Main Conjecture" で,"IMC" と略されることもあります。
岩澤主予想は現在ではかなり一般化されていますが,本記事ではこれまでの記事と同様「イデアル類群の岩澤理論」の範疇に留めたいと思います。また,この記事では「円分 拡大」における岩澤主予想に限定したお話となります。それでも結構難しいのですが,頑張ってついてきてもらえると嬉しいです。
今日の記事は以下の流れで進めます。
かなりの長文(2万3千字)となっていますが,よろしければお付き合いください。
0. 諸注意
この記事を書いているtsujimotterも,実のところまだ理解していないことだらけです。それでも今の時点の理解を記録しておきたくて本記事を書いています。誤りがあった場合はごめんなさい。
また本記事では,参考文献に挙げた本の知識を前提としている箇所もあり,いくつかの記号の定義や定理の説明が省略されています。興味を持ってくださった方は,ぜひ巻末の参考文献も合わせてご参照ください。
また,この記事を通して奇素数 を固定します,という定番の注意をしておきます。
円分 拡大の岩澤主予想を「円分岩澤主予想」と呼びます。省略して単に「岩澤主予想」と言ってしまうこともありますが、本記事内では基本的には円分岩澤主予想のことを指しているものと思ってください。
1. 岩澤主予想のこころ
定理の主張を述べる前に,一体どんな定理なのかをざっくりと説明するところから始めます。
参考資料として以下のスライドを紹介します。パラパラとでかまいませんので,まずはご一読ください.
スライドの説明を要約すると,だいたい以下のようになります:
これらの由来の異なる二つの対象が,実は「深く関係している」ことを主張するのが「岩澤主予想」です(スライド15枚目で説明しています)。

「深く関係している」というのはどういう意味なのか。もう少し突っ込んだ話をしましょう。
一つ注意したいのは,イデアル類群もゼータ関数も,まったく由来の異なる対象だということです。したがって,直接的に二つの対象を等式で結ぶことできません。そこで,それぞれの形を少し変えて,元の性質を残しつつ相性のよい形にしてあげる必要があります。
岩澤理論の主要なアイデアは,「 拡大」 という無限に続く体のタワーを考えることでした。
拡大のそれぞれの階層
に対して「イデアル類群(の
-部分)」
をとっていき,
の逆極限をとって
という加群を考えます。これが有限生成ねじれ
加群という都合の良い加群となっており,
がイデアル類群の代わりになる対象です。
を調べることで,各階層のイデアル類群の位数
が得られてしまう,というのが「岩澤類数公式」でした。
tsujimotter.hatenablog.com
一方で「ゼータ関数」の負の整点の値 は,「クンマーの合同式」という関係式を持つなど
進的な性質を有しています。この性質に着目して,ゼータ関数の値を
進的に補完していくと,p進L関数
という性質のよい関数が得られるのでした。
は岩澤代数
の元となります。
tsujimotter.hatenablog.com
イデアル類群の変わりに 加群
を考え,ゼータ関数の代わりに
の元である
を考えるのです。こうすることで両者を同じ土俵に置くことができ,等式で結ぶことができるようになります。

岩澤主予想のイメージ
厳密にいえば上図の式は成り立ちませんので,もう少しだけ修正する必要がありますが,岩澤主予想の主張はおよそ以上の通りです。この等式によって,イデアル類群の性質をゼータ関数(p進L関数)を通して理解できるようになるというわけです。
2. K = Q(μp) としたときの円分岩澤主予想
以下では,前節の話を具体的に定式化していきましょう。分かりやすさを優先するために,まずは本来の円分岩澤主予想より限定された設定に対して定式化します。より一般の設定については,本記事の後半で再度定式化します。
という円分体の上の「円分
拡大
」を考えます。この拡大が円分岩澤主予想の舞台となります。

岩澤類数公式の記事を思い出してみましょう。 の最大不分岐アーベル pro-
拡大を
とすると,そのガロア群
は,有限生成ねじれ 加群となります。この
がイデアル類群側の主役です。
加群
における構造,特に
のパラメータがわかれば,岩澤類数公式によって,
番目の拡大体
のイデアル類群(の
部分)
の大きさがわかるのでした。

こんなイメージで,一旦 の
タワーを建ててから,上から
を覗くことができるのです。
したがって, 加群
のパラメータ
を特定したいというモチベーションが出てきます。
は有限生成ねじれ
加群なので,
加群の構造定理より,
という擬同型が存在します。
特性イデアルは, が有限生成ねじれ
のときに定義できて,この右辺の基底となる多項式
を掛け合わせて
として得られます。これは の単項イデアルとなります。
の次数を掛け合わせて得られる不変量が
でした。特に,Ferrero-Washington の定理によって,
がアーベル体の場合は
であることがわかっているので,特性イデアルが分かれば
が特定できてしまいます。
実をいうと岩澤主予想は, についてのもう少しだけ精密な情報を教えてくれます。類数公式では,
拡大のガロア群
の作用だけを考えていました。
は
上のアーベル拡大体なので,
上の拡大として考えることができます。ガロア群は
となるため, だけでなく
の作用も考えることにするのです。
ここで,ガロア群の作用を指標により考えるため,円分指標 ,タイヒミュラー指標
を固定します。また,
は巡回群より,
の指標
は
と書くことができます
。したがって,
の指標による直和分解によって
と書けることになります。
は
加群であり,有限生成ねじれ
加群です。
についての
加群としての不変量
が得られれば,より精密な類数公式を得ることができます。
についての作用も含めて考えるというのがポイントです。
さて円分岩澤主予想は, の特性イデアルが,p進L関数を使って表すことができるということを主張します。
ただし,上式は のイデアルとしての等式である.
として捉えると,
を法
のディリクレ指標とみなすことができます。したがって,
をディリクレ指標とするp進L関数を考えることができます。p進L関数
は
の元なので,右辺は
の生成する
の単項イデアルとなります。これが,左辺の特性イデアル(これも単項イデアル)と一致するというわけですね。
3. 岩澤主予想によってわかること
さて,岩澤主予想のステートメントの説明をしてきましたが,このままだとわかったようなわからないような感じですよね。
ここでは,円分岩澤主予想の応用として得られる定理をいくつか紹介したいと思います。まずは,次の定理です。
が成り立つ.
のイデアル類群
の位数が,L関数の値によって書くことができるというもので,深い定理です。
重要な定理なので証明をしましょう。といいつつ,私も少し自信がないのですが,理解できた範囲で書いてみたいと思います。誤りがあるかもしれませんので,正確な内容を知りたい方は「数論2」の定理10.37の証明と関連する項目を読んでください。
簡単に表記するため
とかける.擬同型の定義より
なる完全列が存在する.
を
の生成元とすると,
であり,また「 が奇数のとき,
は有限生成自由
加群」という事実から,
は単射となる.よって,
.
したがって,次のような完全系列の可換図式が存在する:

まず,真ん中の行の という準同型であるが,左から「
倍写像」「
倍写像」「
倍写像によって
の上に誘導される写像」である.
また,一番左の縦の列の系列は
より得られる.真ん中の縦の列の系列は少しややこしい. に着目して考えればわかるかもしれない.
の余核は, を
の
倍で割った群になるから,
として考えれば,
が成り立つことがわかる.この直和をとればいい.
そして,一番右の縦の列の系列は
となる.擬同型の定義から は有限より,四項関係式から
が成り立つ.
以上を踏まえて,蛇の補題より,以下の緑色の完全系列が得られる:
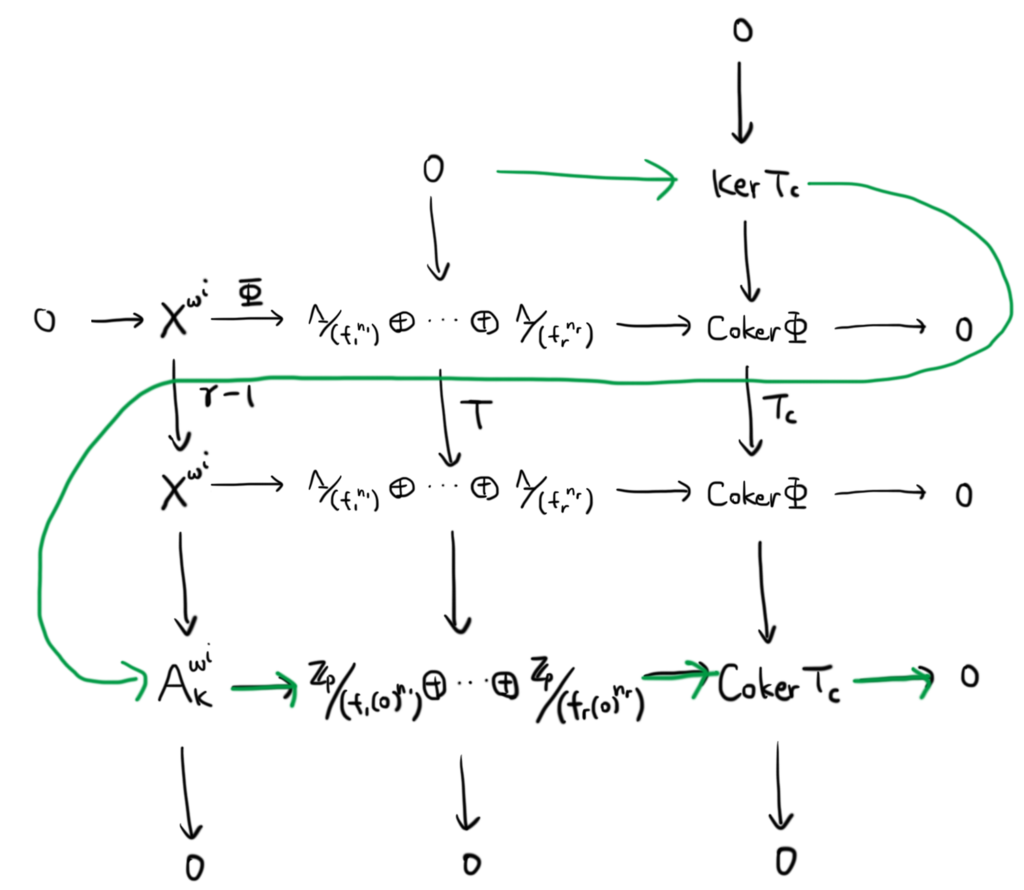
よって,
が成り立つ.したがって,四項関係式から
が得られる.
ここで 円分岩澤主予想(定理1) より,
が成り立つ.したがって,
が成り立つ.ここで,p進L関数の補間性質 を使った.
以上で目的の式が示された.
結構長かったですね。蛇の補題が便利だなと感じました。また,岩澤主予想が肝心なところで使われることが分かったかと思います。
さて,上の定理から エルブラン・リベの定理 もただちに導くことができます。
(1)
(2)
と,定理2より同値性が言える.
また,定理2は以下のように言い換えることができます。こちらの方がエルブラン・リベよりも深い定理になります。
が成り立つ.
となる.したがって,位数をとると定理2より系4が導かれる.
エルブラン・リベの定理(系3)は,
と主張しています。すなわち「 がイデアル類群の位数を少なくとも1回割る」ということがわかります。
一方,系4はより深い情報をもっていて,
のようにイデアル類群(の 部分)の位数を(
の作用付きで),L関数によって完全に特定できるというわけです。すごいですね。
個々の階のようすを個別に調べるのではなく,それらをすべて含んだ 拡大という非常に大きなタワーを建設することで,そのタワーの個々の階のようすが詳細にわかってしまう,というのが岩澤理論の面白いところかと思います。
MathPowerというイベントで「岩澤主予想によって,イデアル類群の構造を完全に特定できる」という旨の発言をしてしまったのですが,厳密に言えば誤りです。岩澤主予想によってわかるのは,あくまで特性イデアルの情報であり,特性イデアルからわかるのは構造定理に関する「位数」の情報です。たとえば構造定理の基底が平方因子を持つかどうかといった情報はわかりません。
イデアル類群の構造をより深く理解するために,特性イデアルの代わりに「Fittingイデアル」を用いた「岩澤主予想の精密化」も知られているそうです。この辺りも理解できたら楽しそうですね。
4. より一般の円分岩澤主予想
先ほどは として限定的な円分岩澤主予想を論じましたが,ここでは落合先生の本に載っているような,より一般的な場合の定式化を考えましょう。
なる自然数
に対して,導手が
(
または
)のディリクレ指標
を考えます。この指標の
に対応する
上の有限次アーベル拡大体を
とします。この体
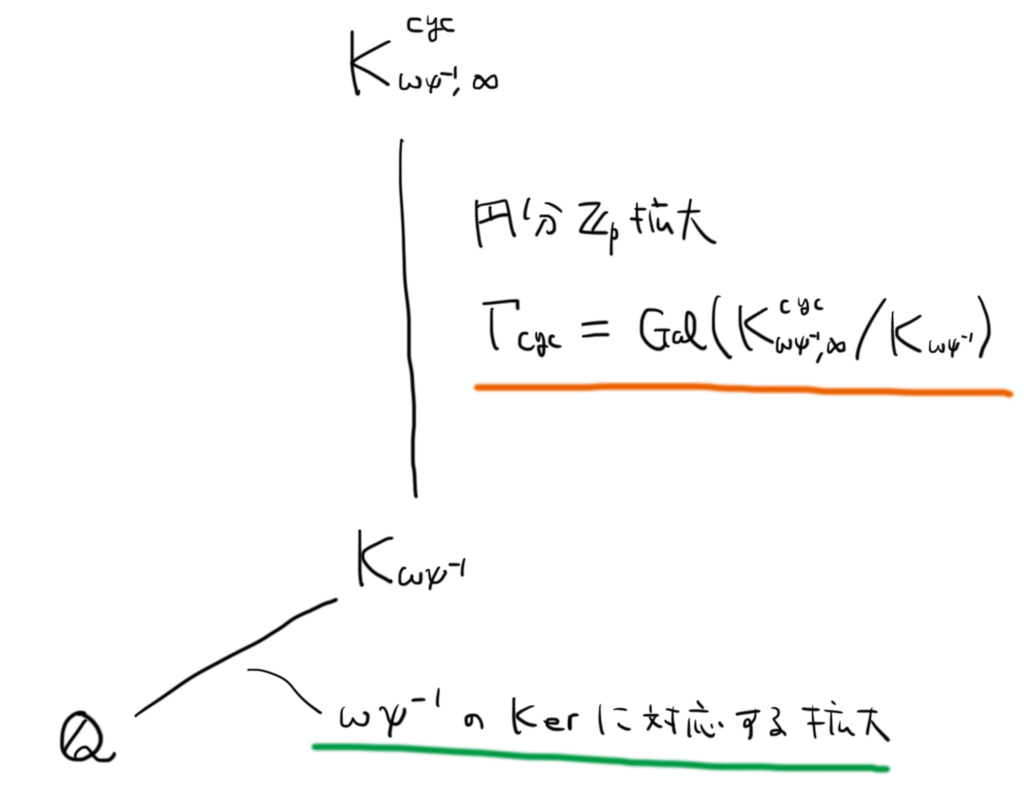
上の円分
拡大
を考えるのです。
拡大のようすを図に表すと以下のようになります。
このような拡大に対して, 加群
を考えます。定式化のために
商を定義します。
ここで,
は
が
で作用するような,
の最大商加群である.また,自然に
加群の構造をとる.
以上の準備のもと,円分岩澤主予想が以下の通り得られます:
が成り立つ.
この定理5が,定理1の一般化となっていることを示しましょう。
また, とすると
となり,
の条件となってしまうので,ここでは
とします。
すると, なる奇数に対して,定理1の結果を導くことができます。
をそのまま代入すると,
となります。したがって,
が得られます。 が奇数のとき
となるため
となって,定理5は定理1を含むことが示されました。
定理1は「導手 のディリクレ指標」に対する円分岩澤主予想だったわけですが,定理5の方は,これを一般化した「導手
のディリクレ指標」に対する円分岩澤主予想となっているわけですね。
定理1のほうが「数論2」で紹介されていた岩澤主予想で,定理5は「落合先生の本」で紹介されているものです。2つの本の記述がまるで異なるので,本当に同じものをさしているのか不安だったのですが,対応関係がとれたことで安心できました。一方の本で理解したことを別の本の記述に翻訳して理解できるようになり,まさにロゼッタストーンを手に入れたという気持ちです。
以上は「 版の円分岩澤主予想」と呼ばれるものです。実は,
版の対にあたる「
版の円分岩澤主予想」もありますので,紹介しておきましょう。
版では
が主役でしたが,
版では
という新しい加群を考えます。
岩澤類数公式の記事で言及したように, はイデアル類群に対応する群です。類体論から
とかける( は「最大不分岐アーベルpro-
拡大」)ので,右辺の逆極限をとって
が定義されるのでした。
一方, では「
の外不分岐な最大アーベルpro-
拡大
」を考えます。「
の外不分岐」とは,
の上にある
上の素点では分岐は許すが,それ以外の素点では不分岐であるような拡大のことです。このような拡大の中で最大のものを考えます。最大不分岐拡大の類似と思ってもらえればオーケーです。そして,この拡大は不分岐アーベルpro-
拡大よりも大きくなります。このような拡大のガロア群をとって,
が定義されます。
と異なり,
は有限生成ねじれ
加群ではない,というのが注意点です。したがって,このままでは特性イデアルが定義できませんが,
が偶指標ということから
がねじれ
加群となります。
このほか記号の説明は省略しますが(詳細は落合先生の上巻を参照),以下が成り立ちます。
が成り立つ.
以上の2つが円分岩澤主予想の定式化となります。
5. 岩澤主予想の証明の方針
さて,ここで気になってくるのが円分岩澤主予想の証明方法だと思います。ここでは,証明の方針だけ紹介したいと思います。
方針を述べるにあたって,まずは と
の関係について述べておく必要があります。詳細は述べませんが,
上の「クンマー・ペアリング」を考えることで,
と
が同値であることが示せます。したがって,どちらか一方を証明すれば良いのです。
また,岩澤主予想はどちらも「 のイデアル」における等号を示すことになります。記法を省略して簡単に書くと
という形の式でした。したがって,
という2つの包含関係を示す必要があります。
ところがです。「解析的類数公式の原理」という定理があって, のすべての指標
に対して,上記の包含のいずれか一方が成り立つことを証明できれば,もう一方の包含関係が自動的に示されてしまうのです。
以上から「 と
のいずれか」そして「イデアルの包含関係のどちらか一方(ただし,すべての指標に対して)」を示せば十分であることがわかります。とても面白いですね。
さて,このように話を整理した上で,岩澤主予想の証明の方法には大きく 2通り の方法が知られています。
一つが,モジュラー的な方法です。これは,Mazur と Wiles によって編み出された方法で,モジュラー形式を経由して証明する方法です。
もともと,エルブラン・リベの定理の「リベによる証明」が,モジュラー形式を経由した証明法でした。Mazur-Wiles はリベの方法を一般化し,岩澤主予想を証明できるレベルまで洗練させたのです。
モジュラー的な方法では, 版の岩澤主予想が得られます。この場合は,
の包含関係が得られます。
もう一つが,オイラー・システム(Euler system)を用いた方法 です。オイラー・システムは Kolyvagin によって発見されましたが,オイラー・システムを用いた岩澤主予想の証明は Rubin によってなされました。
オイラー・システムは,よい条件を持った円分体の単数の元のなす数列のことです。この数列の性質を使ってイデアル類群の大きさをコントロールし,包含関係を示すことができるのです。
オイラー・システムを用いた証明によって, 版の岩澤主予想が得られます。この場合は(面白いことに)逆向きの包含
が得られることになります。
6. 歴史的な経緯について
最後に,歴史的な経緯と関連する研究について補足したいと思います。
まず岩澤主予想は,岩澤理論の創始者である岩澤健吉先生の論文(1964年)によって定式化されました。
その後,Mazur-Wilesの論文(1984年)によって かつ
が
の位数(
)を割らないというケースにおいて解決されました。その後,Wiles自身によって条件が外され,さらに一般的なケースにおいて岩澤主予想が証明されました(1990年)。本記事では「
上のアーベル拡大」についてしか考慮していませんが,Wilesの論文では「総実代数体のアーベル拡大」へと一般化されています。この論文では「肥田理論」が用いられているそうです。
ところで,今回紹介したものは「イデアル類群の岩澤主予想」で,左辺にはイデアル類群を考えるものでした。イデアル類群ではない場合の岩澤理論というものも考えられています。
たとえば,Mazurによって「楕円曲線の(GL(2)の)岩澤理論」が定式化されました。楕円曲線の岩澤理論では,イデアル類群の代わりに「セルマー群」が,p進L関数の代わりに「Hasse-Weil L関数のp進L関数」が考えられます。
さらに,近年ではより一般的な岩澤理論も考えられています。こうした岩澤理論においても「基本予想ABC」という予想群があって,そのうち「基本予想C」として岩澤主予想に相当する予想が定式化されます。
ちなみに,楕円曲線の岩澤主予想についてはRohlich-Rubin, Rohlich-Kato, Skinner-Urbanらの研究によって解決されています。しかしながら,より一般的な岩澤理論においては未解決のものも多いそうです。
以上の通り、岩澤理論は古典的な「イデアル類群の岩澤理論」を超えて広がりを見せており,その多くのケースにおいては岩澤主予想は未解決です。こうした事情もあって「岩澤主予想」と「定理」ではなく「予想」と名が付いて呼ばれているのだろうと(私は)考えています。
楕円曲線の岩澤主予想は,楕円曲線が「虚数乗法を持つ」か「虚数乗法を持たない」かで場合分けされるのですが,虚数乗法を持つケースにおいては,Rohlich-Rubinによって解決されています。そこで,虚数乗法を持たないケースを考えます。
実は,楕円曲線の岩澤主予想においては,解析的類数公式の原理が使えません。したがって,包含関係の両側を示す必要があります。
Rohlich-Katoの方法が,オイラー・システムに基づく方法で の包含関係を示しています。一方で,Skinner-Urbanの方法はモジュラー的な方法で
の包含関係を示すことができます。かくして,両側の包含が示され、虚数乗法を持たないケースが解決します。
要するに,楕円曲線の岩澤主予想においては,岩澤主予想の証明が2通りあったことが本質的に重要だったというわけです。面白いですね。
7. おわりに
以上で,岩澤理論の三本柱である「岩澤類数公式」「p進L関数」「岩澤主予想」を紹介することができました。
去年の今頃に「数学カフェ」というイベントの忘年会がありまして,そこで2017年の目標を述べる機会がありました。そのときに私が述べた目標は「Iwasawa2017 に向けて岩澤理論を理解したい」だったのです。個人的な印象としては,目標はある程度達成できたのではないかと思っています。

当初はなかなか難しいだろうと思っていたのですが,朝に早起きして勉強する「朝岩澤理論」を実行したり,プレゼンの回数を意図的に減らしてインプットに専念したおかげで,それなりのレベルで理解できるようになったと思います。今日のブログ記事は,一年間の成果発表のつもりで書きました。
しかしながら,まだまだ課題は残っています。
一つは,まだ細部をきちんと理解できていないことです。定義を理解しきれていないところもありますし,この記事でもそうでしたが証明もところどころ飛ばしています。また,「モジュラー的な方法」や「オイラー・システムを用いた方法」による岩澤主予想の証明もきちんと追いかけて,tsujimotterのノートブックで解説できるようになりたいと思っています。
もう一つは,私の説明に関してです。あくまで私の個人的な意見ですが「人にわかりやすく解説できてはじめて理解できたといえる」と思っています。ここまで3本ほど岩澤理論の記事を書いていましたが,まだまだ人に伝えられるレベルにありません。自分が理解した範囲をとりあえずまとめた程度にとどまっています。人にわかりやすく伝えるためには,私自身のさらなる理解が必要と考えています。
来年も引き続き岩澤理論を勉強していきたいと思います。もっと高いレベルの理解を目指して。
ところで,数学セミナーという雑誌の1月号(12/12発売)では「岩澤理論」の特集が組まれるらしいのです。なんてこった。
数学セミナー2024年4月号|日本評論社
の次号予告参照。
このニュースを知って,本記事はこの特集が発売される前に書き上げたいと思うようになりました。なぜなら,この特集を読んだ後では,私の理解が更新され,見え方が変わってしまっていると予想されるからです。発売された後で,全然理解していなかったことが明らかになるかもしれません。それはそれで恥ずかしいのですが,それでも今の時点での理解をブログに残しておきたかったのです。きっと書き換えたくなると思うけど,それでいいのだと思っています。
というわけで,長々と発表会に付き合ってくださってありがとうございます。本記事がきっかけで岩澤理論に興味を持ってもらえたら嬉しいです。
それでは,今日はこの辺で。
参考文献
本記事は,以下の2つの本を主に参考にしながら書きました。
以下の本も私の理解の役に立ちました。

