コーツ・ワイルズの定理（のあらすじ）

　7/19から7/28の計9日間，Iwasawa2017という国際研究集会が東京大学にて開催されました．岩澤理論における世界的スーパースターが一堂に会し活発な議論が行われました．

f:id:tsujimotter:20170729000650j:plain:w200

　実はtsujimotterもこっそり参加しておりました．感想やレポートはまたいずれ書きたいと思いますが，今日は別のお話をしたいと思います．

　今日は，Iwasawa2017の講演者の一人であるジョン・コーツ先生*1の結果の中で，私のお気に入りの定理「コーツ・ワイルズの定理」についてご紹介したいと思います．

　コーツ・ワイルズの定理は，コーツ先生とその教え子であるアンドリュー・ワイルズの共同研究として，1977年に発表された定理です．当時最先端だった岩澤理論を用いて，BSD予想という（今も未解決の）問題に対する最初の足掛かりを与える結果でした．定理の主張自体も十分にすごいのですが，証明の流れも魅力的なものだと感じました．その魅力をお伝えしたいと思ってこの記事を書いています．コーツ・ワイルズの定理とその証明の面白さについては，私の数学仲間であるせきゅーんさんに教えていただきました．せきゅーんさんには，この場を借りて御礼申し上げます．

　コーツ・ワイルズの定理の証明は，こちらの論文で見ることができます．

On the conjecture of Birch and Swinnerton-Dyer | SpringerLink

　定理の主張と証明のあらすじについては，落合先生によって書かれたPDFで知りました．

http://www.math.sci.osaka-u.ac.jp/~ochiai/wiles05.pdf

　落合先生は岩澤理論の専門家で，私が勉強している岩澤理論の本の著者の方です．コーツ先生の原論文は私には難しかったので，今回は落合先生のPDFの内容をベースにお話したいと思います．先生のPDFに分かりやすくまとまっているので，正直言うと私の記事にそれほど価値はないのかもしれません．それでもどうしても魅力を伝えたい気持ちが抑えられなくなって，筆をとっています．オリジナル要素としては，私が理解するために考えた道のりを補足的に書き足すことにします．

　今回の内容は「岩澤理論」が関係します．岩澤理論の基礎知識は仮定しますので自信がない方はぜひ以下の記事を読んでみてください．
tsujimotter.hatenablog.com

目次：

1. BSD予想とコーツ・ワイルズの定理

2. 円単数とゼータ関数

3. 証明のあらすじ（コーツ・ワイルズの定理）

4. おわりに

5. 関連記事

1. BSD予想とコーツ・ワイルズの定理

　コーツ・ワイルズの定理の前に，定理の背景，特に「BSD予想」についてお話しておきましょう．

　Birch and Swinnerton-Dyer予想（以下，BSD予想）は，リーマン予想と並ぶミレニアム問題の一つです．今日まで未解決の問題となっています．ミレニアム問題ということもあって名前を知っている人は多いと思いますが，一方で予想の正確な主張を知っている人は多くないかもしれません．

　BSD予想は，楕円曲線の持つランクと呼ばれる量が，楕円曲線の L関数の値と結び付くという興味深い予想です．

　まずは，楕円曲線の基礎事項について，今回の話に必要な範囲でさらっとおさらいします． $\mathbb{Q}$ 上の楕円曲線 $E$ の有理点の集合 $E(\mathbb{Q})$ は，自然に加法を入れることができて，アーベル群をなすことが知られています．さらに， $E(\mathbb{Q})$ はモーデルによって有限生成であることが示されており*2， $E(\mathbb{Q})$ の任意の点 $P$ は有限個の基底 $P_1, P_2, \ldots, P_k$ の整数倍によって，次のように表すことができます．

$P = n_1 P_1 + n_2 P_2 + \cdots + n_k P_k$

　 $E(\mathbb{Q})$ における点は，位数有限の点（何倍かすると元に戻る）と位数無限の点（何倍かしても元に戻らない）の２種類に分類されます．基底 $P_1, P_2, \ldots, P_k$ のうち，位数無限の点の個数を $E(\mathbb{Q})$ のランクといいます．言い方を変えると， $E(\mathbb{Q})$ を有限生成アーベル群の構造定理によって

$E(\mathbb{Q}) \simeq \mathbb{Z}^{\oplus r} \oplus E_{\mathrm{tor}}$

と表したとき（ $E_{\mathrm{tor}}$ は位数有限の点の集合で「ねじれ点（torsion point）」といいます）， $\mathbb{Z}$ の肩に乗っている整数 $r$ がランクです．このランクという量は基底の選び方によらず，楕円曲線 $E$ を考える上で重要な不変量となっています．

　一方で，楕円曲線には対応する L関数を考えることができます．L関数は，楕円曲線を素数 $p$ における局所的な情報によって張り合わせて作られますが，このL関数を通してみると楕円曲線の性質がわかってしまうのです．素数の情報を張り合わせて作った「リーマン・ゼータ関数」を通して，素数の性質を理解することのアナロジーを考えるとわかりやすいかもしれません．

　楕円曲線 $E$ を $\mathbb{F}_p$ 上で考えることを「還元する」といいます． $\mathbb{F}_p$ で還元した楕円曲線の点の個数を $N_p$ として

$a_p(E) = p + 1 - N_p \tag{1}$

という数列を考えたとき，楕円曲線 $E$ のL関数 $L(s, E)$ を以下のように定義します*3：

$\displaystyle L(s, E) = \prod_{p : \mathrm{bad}} \frac{1}{1-a_p(E) p^{-s}} \times \prod_{p : \mathrm{good}} \frac{1}{1-a_p(E) p^{-s}+p^{1-2s}} \tag{2}$

　 $\mathrm{bad}, \mathrm{good}$ と呼ばれる２種類の素数を考えます．それぞれ以下のように定義されます：

$E$ の導手を丁度１回割る素数を bad prime という
$E$ の導手を割り切らない素数を good prime という

　楕円曲線には導手と呼ばれる量があり， $E$ の導手を割り切るかどうかで素数の種類が二分されるのです．

素数が bad か good であるかという区別は，本記事においては本質的ではありませんので，細かいところは気にする必要はありません．とにかく，素数 $p$ ごとに還元して $a_p(E)$ を考えて， $a_p(E)$ からオイラー積を作って $L(s, E)$ を定義されることだけ知っていれば十分です．

　このように定義されたL関数は，複素数 $s$ を変数に持つ複素関数となっています．上記の積は $\displaystyle Re(s) > \frac{3}{2}$ で絶対収束しますが， $\mathbb{Q}$ 上の楕円曲線に対するL関数は，全複素平面に解析接続されることが知られています*4．したがって， $L(s, E)$ は全複素平面で定義できます．

　この $L(s, E)$ の「 $s = 1$ の周りにおける解析的な性質」がなぜか「楕円曲線のランク」と結びついている，ということを主張するのが BSD予想です．

　実際，Birch と Swinnerton-Dyer によって以下のように予想されています．

予想（BSD）

$E$ を $\mathbb{Q}$ 上定義された楕円曲線とする．このとき $L(s, E)$ の $s = 1$ での零点の位数は $E(\mathbb{Q})$ のランクと等しい．

　定理の主張を言い換えると次のようになります． $L(s, E)$ を $s = 1$ の周辺でテイラー展開します．すると

$\displaystyle L(s, E) = A_r (s-1)^r + A_{r+1}(s-1)^{r+1} + \cdots \tag{3}$

のように表すことができて，この $r$ がなぜか $E(\mathbb{Q})$ のランクになっているというのです．

　特殊なケースを考えると， $s \to 1$ が非ゼロのときは，ランクが $r = 0$ すなわち $E(\mathbb{Q})$ が有限群になるということを主張しています．逆に無限群であれば $L(1, E) = 0$ です．

　すなわち，L関数という解析的な対象を調べることで，楕円曲線の有理点に関する情報が復元できると言っているのです．不思議な予想ですね．

　さて，以上の話を踏まえて，コーツ・ワイルズの定理の主張を述べたいと思います．

　コーツ・ワイルズは，特別なケースにおいてBSD予想を部分的に解決しました．正確なステートメントを以下に述べます：

定理（Coates-Wiles/1977）

$E$ は $\mathbb{Q}$ 上の楕円曲線であって，類数１の虚２次体 $K$ が存在して $\newcommand{\endm}{\mathrm{End}_{\overline{\mathbb{Q}}}} \endm(E) \simeq \mathcal{O}_K$ とする．

　このとき，もし $L(1, E) \neq 0$ ならば $E(\mathbb{Q})$ は有限アーベル群である．

　まず「類数１の虚２次体 $K$ が存在して $\endm(E) \simeq \mathcal{O}_K$ とする」という条件つきの定理になっていることがわかります．

　上の条件を除けば，コーツ・ワイルズは（緩和された）BSD予想の半分を解決したことになります．以下の２つの予想

(1) もし $L(1, E) \neq 0$ ならば $E(\mathbb{Q})$ は有限アーベル群（ランクがゼロ）
(2) もし $L(1, E) = 0$ ならば $E(\mathbb{Q})$ は無限群（ランクが正）

を考えるとこれはBSD予想を緩和したものと言えますが，コーツ・ワイルズは条件付きで (1) を解決したことになります．条件付きとはいえBSD予想の部分的解決は史上初めてのことで，予想の解決に向けた大きな一歩であったといえます．

　コーツ・ワイルズの結果は「 $E$ が虚数乗法を持つ」という特殊な条件となっています．詳細は述べませんが，楕円曲線 $E$ の自己準同型環 $\endm(E)$ が $\mathbb{Z}$ より大きく，虚２次体 $K$ の整数環 $\mathcal{O}_K$ に一致するとき $E$ は虚数乗法を持つといいます．楕円曲線は大きく分けて「虚数乗法を持つ」「虚数乗法を持たない」の２通りに分類されますが，ほとんどの楕円曲線は虚数乗法を持たないことが知られていて，虚数乗法を持つのは特例なのです．

　もう一つ虚２次体 $K$ には「類数１である」という条件が付いています．この条件は技術的なもので，後ほど別の数学者によって外されたそうです．

ちなみに「類数１である虚２次体」はたった９つしかないことが知られており，それについては以下の記事で詳細を述べています．
tsujimotter.hatenablog.com

　このコーツ・ワイルズの定理の証明は実際非常に難しいのですが，あらすじくらいなら紹介できるかもしれません．冒頭で述べた通り岩澤理論の道具を使うことになります．

　問題の本質は「楕円曲線の無限性（有限性）」と「L関数のゼロ性（ノンゼロ性）」という全く異なる対象を結び付けることです．この問題を解決するために，岩澤理論で用いられる「楕円単数」という道具を導入します．楕円単数は楕円曲線のL関数と結びつくことが知られています．

楕円単数 $\Theta_p \; \leadsto \; E$ のL関数の関数値 $L(1, E)$

　楕円単数の定義は複雑で，今の私には紹介する力はありません．そこで，楕円単数の親戚である「円単数」について紹介することにします．円単数も同様にL関数（ゼータ関数）の特殊値と結びつくのです．

円単数 $u \; \leadsto \;$ ゼータ関数の関数値 $(1-2^r)\zeta(1-r)$

2. 円単数とゼータ関数

　ここでは「円単数はどのようなもので，それがいかにしてゼータ関数の特殊値と結びつくのか」に焦点をしぼって，そのメカニズムを紹介したいと思います．円単数の話は，ウェブ上で検索してもほとんど情報が出てきませんので，丁寧に紹介しましょう．

　まず，円単数を今回は $u = 1 + \zeta_p$ と定義しましょう． $p$ は素数で， $\zeta_p$ は１の原始 $p$ 乗根です．「今回は」と書いた通り，これはあくまで円単数の例の一つであって，今回のものだけが円単数と呼ばれるわけではないという点に注意してください．

　さて， $u$ は $\newcommand{\zp}{\mathbb{Z}_p} \zp[\zeta_p]$ の元となっています．これをどのように変形したらゼータ関数の特殊値と結びつくのか説明していきましょう．

　まず， $u \in \zp[\zeta_p]$ に対して

$f_u(\zeta_p - 1) = u \tag{4}$

となるべき級数 $f_u(t) \in \zp[[t]]$ を考えます．これをコールマンべき級数といいます．

　実際，

$f_u(t) = 2+t \tag{5}$

とすることで，

$f_u(\zeta_p - 1) = 2+(\zeta_p-1) = 1+\zeta_p = u$

となって， $(6)$ を満たすことがわかります．円単数 $u$ を選ぶと，それに対してコールマンべき級数 $f_u(t)$ が定まるわけです．これは一意に定まるとは限りません．

　 $f_u(t)$ を用いて，以下のような $g_u^{(r)}(t)$ を考えます：

$\displaystyle \newcommand{\d}{\mathrm{d}} g_u^{(r)}(t) = \left( (1+t)\frac{\d}{\d t}\right)^r \log ( f_u(t) ) \tag{6}$

　 $f_u(t)$ の対数をとってから，微分して（ $(1+t)$ をかける）作用を $r$ 回適用しています．この「対数をとってから微分する」というのがポイントです．

　このように定義すると，各正の整数 $r$ に対して $\varphi^{(r)} : \zp[\zeta_p] \to \mathbb{Z}/(p)\mathbb{Z}$ を

$\varphi^{(r)}(u) = g_u^{(r)}(t)\big|_{t=0} \pmod{p}$

として写像が定まります．これをコールマン写像といいます．

　定義が続いたので，一旦整理しましょう．以下の流れで進めてきました．

円単数 $u \in \zp[\zeta_p]$ という特別な元を考える
円単数 $u$ から定まる（一意とは限らない）コールマンべき級数 $f_u(t) \in \zp[[t]]$ を考える
コールマンべき級数 $f_u(t)$ に対して「対数をとって微分する」と $g_u^{(r)}(t) \in \zp[[t]]$ が得られる
$g_u^{(r)}(t)$ に $t=0$ を代入すると $\zp$ の値が得られ，さらに $\bmod{p}$ をとると $u \mapsto g_u^{(r)}(t)\big|_{t=0} \pmod{p}$ としてコールマン写像 $\varphi_u^{(r)}$ が得られる

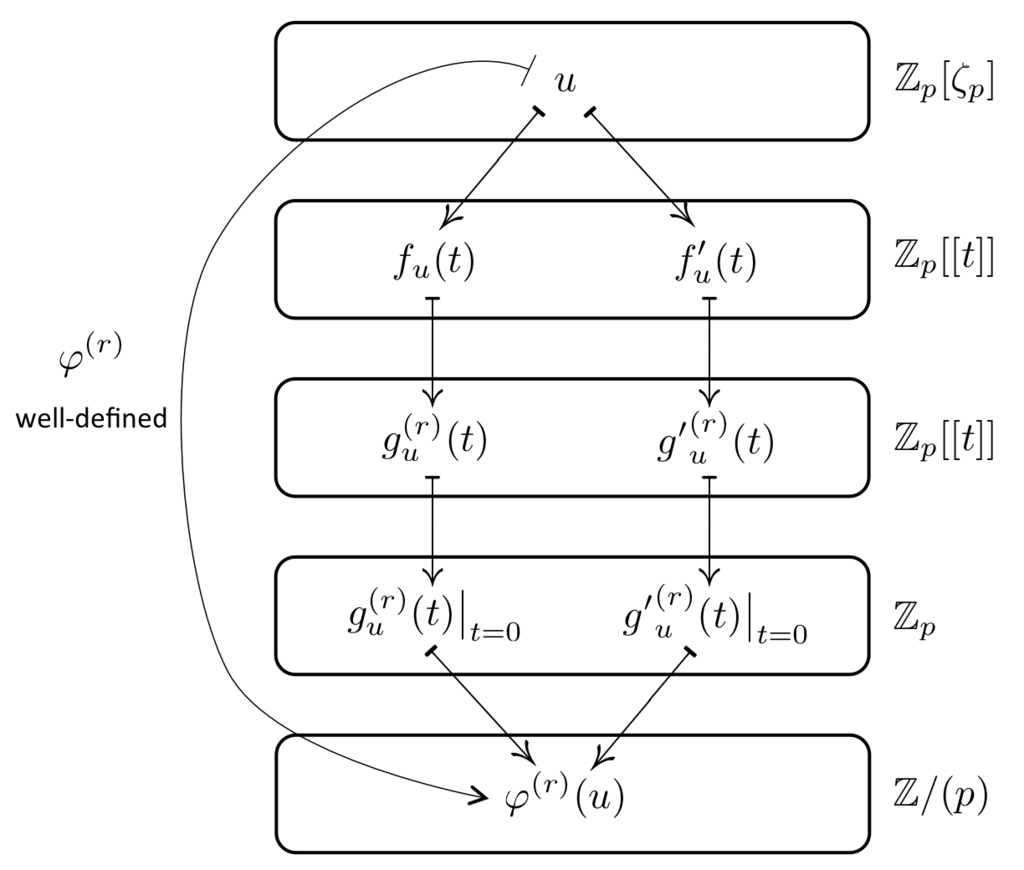
　コールマン写像 $\varphi_u^{(r)}$ は，定義からわかるように $f_u(t)$ の選び方に依存するので，この写像が $u$ に対して一意に定まるかどうか（well-defined かどうか）は明らかではありません．実際， $\bmod{p}$ をとる前の $g_u^{(r)}(t)|_{t=0} \in \zp$ の段階では， $f_u(t)$ の選び方によって異なる値をとります．

　しかしながら， $\bmod{p}$ をとると $f_u(t)$ の選び方による不定性が打ち消され， $u \mapsto g_u^{(r)}(t)\big|_{t=0} \pmod{p}$ は一意に定まります．したがって，コールマン写像は well-defined です．

f:id:tsujimotter:20170724065527p:plain:w300

　さらに言えばコールマン写像は， $u \in \zp[\zeta_p]$ の対する積の演算を $\mathbb{Z}/(p)\mathbb{Z}$ における和に変換します．したがって，コールマン写像は群の演算を保存する準同型写像となります．

　さて，ここまでまだゼータ関数が登場していません．コールマン写像がいったいどうやってゼータ関数と結びつくのでしょうか．

　実は，以上で定義した $\varphi^{(r)}(u)\big|_{t=0}$ は， $\bmod{p}$ でリーマン・ゼータ関数の特殊値 $(1-2^r)\zeta(1-r)$ と合同になります．すなわち，以下が成り立ちます：

$\varphi^{(r)}(u) \equiv (1-2^r)\zeta(1-r) \pmod{p} \tag{7}$

　なんということでしょう！！

　実際にコールマン写像からゼータ関数が出てくることは，実際に計算してみるとわかります．少し骨が折れますが，高校レベルの微積分＋αで計算できますので，興味がある人は一緒に計算してみてください．後の議論には必要ないので，必要ない方は「3. 証明のあらすじ（コーツ・ワイルズの定理）」まで飛ぶとよいでしょう．

（証明）
　円単数を $u = 1 + \zeta_p \in \zp[\zeta_p]$ とします．この $u$ に対してコールマンべき級数 $f_u(t) = 2 + t \in \zp[[t]]$ をとります．

　 $f_u(t)$ の対数をとり，「 $t$ で微分して $1+t$ をかける」作用を $r$ 回繰り返してえられるべき級数を $g_u^{(r)}(t)$ とします．すると

$\begin{align} g_u^{(r)}(t) &= \left( (1+t)\frac{\d}{\d t}\right)^r \log (f_u(t) ) \\ &= \left( (1+t)\frac{\d}{\d t}\right)^r \log (2+t) \end{align}$

　 $t = T - 1$ と変数変換すると， $dt = dT$ となり $t = 0$ のとき $T = 1$ となります．よって，

$\displaystyle \begin{align} &= \left( T\frac{\d}{\d T}\right)^r \log (1+T) \\ &= \left( T\frac{\d}{\d T}\right)^{r-1}T\frac{\d}{\d T} \log (1+T) \\ &= \left( T\frac{\d}{\d T}\right)^{r-1} \frac{T}{1+T} \end{align}$

　さらに， $T = \exp(x)$ と変数変換すると， $dT = dx \exp(x)$ となり $T = 1$ のとき $x = 0$ となります．よって

$\displaystyle = \left( \frac{\d}{\d x}\right)^{r-1} \frac{e^x}{1+e^x}$

を得ます．

　結局，

$\displaystyle \varphi^{(r)}(u) = g_u^{(r)}(t) \bigg|_{t=0} = \left( \frac{\d}{\d x}\right)^{r-1} \frac{e^x}{1+e^x}\Bigg|_{x=0}$

が得られます．

　これをそれぞれの $r$ について実際に計算すると $\varphi^{(r)}(u)$ からゼータ関数の値が個別に得られます．しかし，以下のように個別の計算ですら非常に面倒ですし，一般的な法則は得られないので別の方法を取ります．

$r = 1$ のとき：

$\displaystyle \varphi^{(1)}(u) = \frac{e^x}{1+e^x}\Bigg|_{x=0} = \frac{1}{2}$

　一方， $(1-2^r)\zeta(1-r)$ に $r=1$ を代入すると，

$\displaystyle (1-2^1)\zeta(1-1) = -\zeta(0) = \frac{1}{2}$

となり一致．

$r = 2$ のとき：

$\displaystyle \varphi^{(2)}(u) = \frac{\d}{\d x}\frac{e^x}{1+e^x}\Bigg|_{x=0} = \frac{e^x(1+e^x) - e^x\cdot e^x}{(1+e^x)^2}\Bigg|_{x=0} = \frac{1}{4}$

　一方， $(1-2^r)\zeta(1-r)$ に $r=2$ を代入すると，

$\displaystyle (1-2^2)\zeta(1-2) = -3\zeta(-1) = \frac{1}{4}$

となり一致．

$r = 3$ のとき：

$\displaystyle \begin{align} \varphi^{(3)}(u) &= \left( \frac{\d}{\d x}\right)^{2} \frac{e^x}{1+e^x}\Bigg|_{x=0} \\ &= \frac{\d}{\d x}\frac{e^x}{(1+e^x)^2}\Bigg|_{x=0} \\ &= \frac{e^x(1+e^x)^2 - 2e^x(1+e^x)e^x}{(1+e^x)^4}\Bigg|_{x=0} \\ &= \frac{1\cdot(1+1)^2 - 2(1+1)\cdot 1}{(1+e^x)^4}\Bigg|_{x=0} = 0 \end{align}$

　一方， $(1-2^r)\zeta(1-r)$ に $r=3$ を代入すると，

$\displaystyle (1-2^3)\zeta(1-3) = -7\zeta(-2) = 0$

となり一致．

　さて，ここで

$\displaystyle \varphi^{(r)}(u) = \left( \frac{\d}{\d x}\right)^{r-1} \frac{e^x}{1+e^x}\Bigg|_{x=0}$

は， $\displaystyle \frac{xe^x}{1+e^x}$ のテイラー展開における $r$ 次の係数の $(r-1)!$ 倍である．

　このことは以下のようにしてわかる．

$\displaystyle \frac{e^x}{1+e^x} = a_0 + a_1 x + \frac{a_2}{2!}x^2 + \cdots + \frac{a_r}{r!}x^r + \cdots$

のようにテイラー展開する． $r-1$ 回微分すると

$\displaystyle \left( \frac{\d}{\d x}\right)^{r-1}\frac{e^x}{1+e^x} = a_{r-1} + a_{r} x + \cdots$

となり， $x = 0$ を代入すると $a_{r-1}$ が出てくる． $\varphi^{(r)}(u)$ の定義より

$\displaystyle \varphi^{(r)}(u) = \left( \frac{\d}{\d x}\right)^{r}\frac{e^x}{1+e^x}\Bigg|_{x=0} = a_{r-1}$

が得られる．

　また， $\frac{xe^x}{1+e^x}$ は $\frac{e^x}{1+e^x}$ に $x$ をかけたものであるから， $\frac{xe^x}{1+e^x}$ のテイラー展開は

$\displaystyle \begin{align} \frac{xe^x}{1+e^x} &= a_0 x + a_1 x^2 + \frac{a_2}{2!}x^3 + \cdots + \frac{a_{r-1}}{(r-1)!}x^{r} + \cdots \\ &= \varphi^{(1)}(u) x + \varphi^{(2)}(u) x^2 + \frac{\varphi^{(3)}(u)}{2!}x^3 + \cdots + \frac{\varphi^{(r)}(u)}{(r-1)!}x^{r} + \cdots \\ &= \sum_{n=1}^{\infty} \frac{\varphi^{(n)}(u)}{(n-1)!}x^{n} \end{align}$

とかける．

　結論として，

$\displaystyle \frac{xe^x}{1+e^x} = \sum_{n=1}^{\infty} \frac{\varphi^{(n)}(u)}{(n-1)!}x^{n} \tag{8}$

が得られる．

　またここで，

$\displaystyle \frac{xe^x}{1+e^x} = \frac{(2x)e^{2x}}{e^{2x}-1} - \frac{xe^x}{e^x - 1} \tag{9}$

も成り立つ．

（証）

$\displaystyle \frac{(2x)e^{2x}}{e^{2x}-1} = \frac{(2x)e^{2x}}{(e^{x}-1)(e^{x}+1)}$

から

$\displaystyle \frac{xe^{x}}{e^{x}-1} = \frac{xe^{x}(e^{x}+1)}{(e^{x}-1)(e^{x}+1)}$

を引き算すると

$\displaystyle \begin{align} \frac{(2x)e^{2x}}{e^{2x}-1} - \frac{xe^x}{e^x-1} &= \frac{2xe^{2x} - xe^x(e^x+1)}{(e^x-1)(e^x+1)} \\ &= \frac{xe^x(e^x-1)}{(e^x-1)(e^x+1)} \\ &= \frac{xe^x}{e^x+1} \end{align}$

　ここで，ベルヌーイ数 $B_n$ の定義より

$\displaystyle \frac{xe^{x}}{e^{x}-1} = \sum_{n=0}^{\infty} \frac{B_n}{n!}x^n \tag{10}$

であったことを思い出しましょう．

　 $(10)$ 式に $x \leftarrow 2x$ とすると

$\displaystyle \begin{align} \frac{(2x)e^{2x}}{e^{2x}-1} &= \sum_{n=0}^{\infty} \frac{B_n}{n!}(2x)^n \\ &= \sum_{n=0}^{\infty} \frac{2^n B_n}{n!}x^n \end{align} \tag{11}$

となります．

　 $(10), (11)$ 式を $(9)$ 式に代入すると

$\displaystyle \begin{align} \frac{xe^x}{1+e^x} &= \frac{(2x)e^{2x}}{e^{2x}-1} - \frac{xe^x}{e^x - 1} \\ &= \sum_{n=0}^{\infty} \frac{2^n B_n - B_n}{n!}x^n \\ &= - \sum_{n=0}^{\infty} \frac{(1 - 2^n) B_n}{n!}x^n \end{align}$

　これが $(8)$ 式と一致するから， $r$ 次の係数同士を比較して

$\displaystyle \frac{\varphi^{(r)}(u)}{(r-1)!} = -(1 - 2^r) \frac{B_r}{r!}$

が得られる．すなわち

$\displaystyle \varphi^{(r)}(u) = -(1 - 2^r) \frac{B_r}{r}$

である．

　ゼータ関数の特殊値とベルヌーイ数のよく知られた関係

$\displaystyle -\frac{B_r}{r} = \zeta(1-r) \tag{12}$

より

$\displaystyle \varphi^{(r)}(u) = (1 - 2^r)\zeta(1-r)$

が得られました．

（証明終わり）

　長かったですが，結局以下のような準同型が得られたことになります．

f:id:tsujimotter:20170724071655p:plain:w280

　すなわち， $\zp[\zeta_p]$ から $\bmod{p}$ でゼータの特殊値に合同な写像が作れるということです．

　今は $\zp[\zeta_{p}]$ で考えましたが，実はこれを $\zp[\zeta_{p^{n+1}}]$ に拡張することができます． $n \geqq 0$ に対して $\zp[\zeta_{p^{n+1}}]$ から「 $\bmod{p^{n+1}}$ でゼータの特殊値に合同な値」への写像を作ることができるのです．

　このような条件を満たす $\zp[\zeta_{p^{n+1}}]$ の元を $u_n$ とし，数列 $(u_n)_{n\geqq 0}$ を考えます（ $\bmod{p}$ の場合の $u_0$ は $u_0 = u$ と定義しておきます）．

　以上の数列に，ノルム写像 $N_{n,n-1} : \zp[\zeta_{p^{n+1}}] \to \zp[\zeta_{p^{n}}]$ を定義すると

$\cdots \longmapsto u_n \longmapsto u_{n-1} \longmapsto \cdots \longmapsto u_2 \longmapsto u_1 \longmapsto u_0$

という系列を作ることができ，これをノルム系といいます．ノルム写像によるノルム系の逆極限

$\displaystyle \mathbf{u} = \varprojlim_{n} u_n$

を考えると

$\displaystyle \varprojlim_{n} \zp[\zeta_{p^{n+1}}] \ni \mathbf{u} \longmapsto \varphi^{(r)}(\mathbf{u}) \in \zp$

という写像を構成することができます．

　今説明した方法を一般化したものが「p進L関数のコールマン写像を用いた構成法」です．前回紹介したp進L関数は，以上のような方法によって実際に構成することができるのです．
tsujimotter.hatenablog.com

3. 証明のあらすじ（コーツ・ワイルズの定理）

　それでは，これまでの道具を使って，定理を証明するためのあらすじを説明しましょう．

　まず，この証明の魅力を３点紹介します．

虚数乗法が関連している点
岩澤理論（楕円単数）を使っている点
「L関数＝ゼロ」を示す方法が超かっこいい点

　１つめの「虚数乗法」は名前がかっこいいので好きです．２つめの「岩澤理論」は私が個人的に勉強していて魅力的に感じています．そして，３つめは証明のかっこよさです．あとで強調しますが「ゼロ」という数の持つ特性をうまくつかいます．ほんとにかっこいい．

　証明の方針ですが，コーツ・ワイルズの定理の主張は

$L(1, E) \neq 0 \; \Longrightarrow \; E(\mathbb{Q})$ は有限アーベル群

でしたが，この命題の対偶をとることにします．すなわち

$E(\mathbb{Q})$ は無限群 $\; \Longrightarrow \; L(1, E) = 0$

を示します．したがって， $E(\mathbb{Q})$ は無限群が証明に用いる仮定となります．

（証明のあらすじ）
　 $\mathbb{Q}$ 上の楕円曲線を $E$ として， $\endm(E) \simeq \mathcal{O}_K$ となる類数１の虚２次体を $K$ とします．虚２次体 $K$ において， $p = \pi \overline{\pi}$ と分解する素数 $p$ をとります（★）．

　 $[\pi^r] \in \endm(E)$ を $\pi^r \in \mathcal{O}_K$ に対応する $E$ の自己準同型とし， $\mathrm{ker}([\pi^r]) \subset E(\overline{\mathbb{Q}})$ の座標をすべて $K$ に付け加えた拡大を $K(\pi^r)$ とします．

　この辺で「虚数乗法」について補足しておきたいと思います．

　楕円曲線の点の集合 $E(\overline{\mathbb{Q}})$ にはアーベル群の構造が入るので，その点 $P \in E(\overline{\mathbb{Q}})$ には自然に $n$ 倍写像 $[n]$ という自己準同型を定義できます．

　ここで楕円曲線によっては， $n$ 倍ではない自己準同型を持つものも（例外的に）存在します．このような自己準同型は上のように $\alpha \in \mathcal{O}_K\backslash \mathbb{Z}$ の元と対応付けて「 $\alpha$ 倍写像」と呼ぶことにします．楕円曲線が「整数倍よりも大きな対称性を持つこと」を，楕円曲線 $E$ は虚数乗法を持つといいます．

　 $n$ 倍して $O$ に一致する $E$ の点全体，すなわち

$\mathrm{ker}([n]) \subset E(\overline{\mathbb{Q}})$

を $E$ の $n$ -等分点といいます．同様に $\alpha$ 倍写像によって $O$ に一致する $E$ の点全体，すなわち

$\mathrm{ker}([\alpha]) \subset E(\overline{\mathbb{Q}})$

によって「 $\alpha$ -等分点」を考えることができます．

　クロネッカー・ウェーバーの定理により，円の $n$ -等分点によって $\mathbb{Q}$ 上のアーベル拡大を作ることができましたが，このアナロジーが虚２次体 $K$ においても成り立ちます．虚数乗法を持つ楕円曲線の $\alpha$ -等分点によって $K$ 上のアーベル拡大を作ることができます．

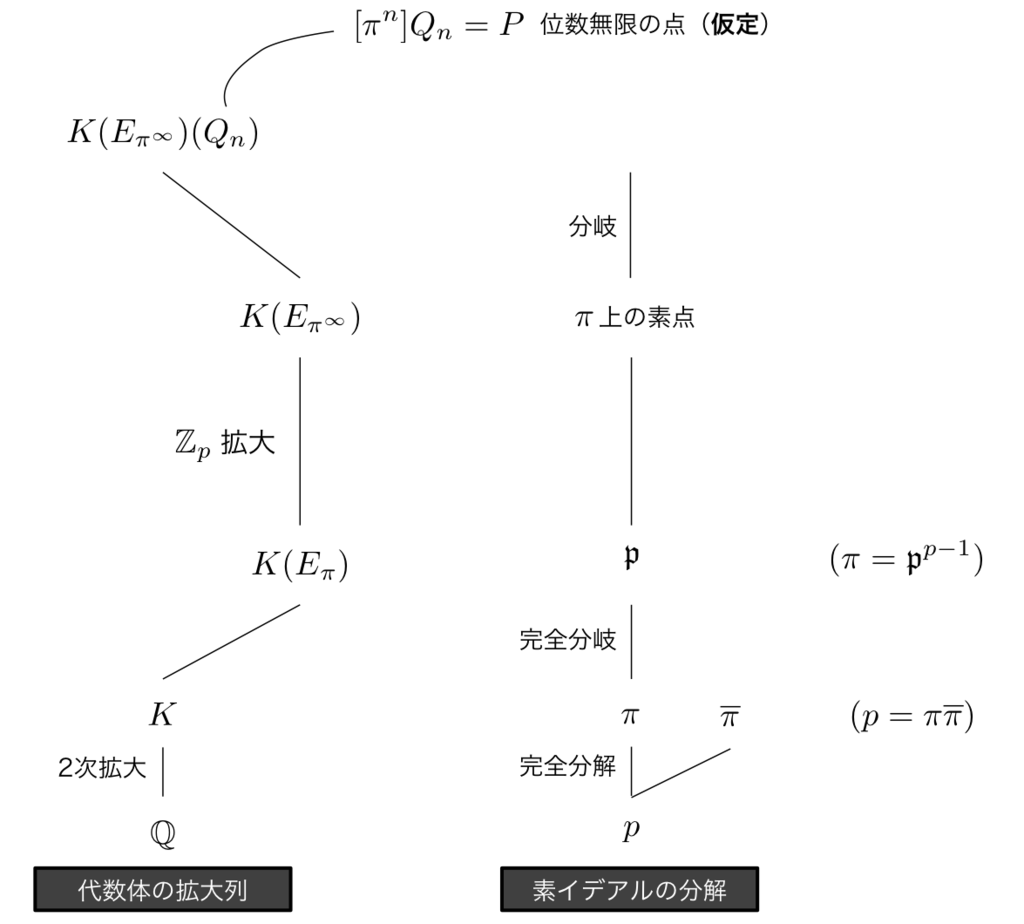
　 $n = 1, 2, 3, \ldots$ に対して $K(E_{\pi^n})$ を合成した体を $K(E_{\pi^\infty})$ とします．すなわち

$\displaystyle K(E_{\pi^\infty}) = \bigcup_{n=1}^{\infty}K(E_{\pi^n})$

とします．実はこの拡大が $K(E_{\pi})$ 上の $\zp$ 拡大となっています．

f:id:tsujimotter:20170724065607p:plain:w240

円の $p^n$ 等分点を $\mu_{p^n}$ として，

$\displaystyle \mathbb{Q}(\mu_{p^\infty}) = \bigcup_{n=1}^{\infty}\mathbb{Q}(\mu_{p^n})$

という $\zp$ 拡大があったことを思い出しましょう．

　ここで仮定を使います．仮定より位数無限の点 $P \in E(\mathbb{Q})$ があります．

　 $[\pi^n] Q_n = P$ なる $Q_n \in E(\overline{\mathbb{Q}})$ の座標を付け加えて，巡回拡大 $K(E_{\pi^\infty})(Q_n)/K(E_{\pi^\infty})$ が得られます．

$K(E_{\pi^\infty})$ よりさらに大きな拡大を考えることになります．

　ここからさらにがんばると，次の LEMMA 1 を証明することができます．

LEMMA 1

$K(E_{\pi^\infty})(Q_n)/K(E_{\pi^\infty})$ は，十分大きな $n$ において $\pi$ 上の素点で分岐する．

　この定理を証明することが，コーツ・ワイルズの論文における最重要ポイントだったようです．落合先生のPDFによると，コーツ・ワイルズの論文では２種類の方法によってこれを証明しています．

　一方で， $K(E_{\pi})$ は $K$ 上の完全分岐拡大であり， $\mathcal{O}_{K(E_\pi)}$ では $(\pi) = \mathfrak{p}^{p-1}$ となります（完全分岐）．

さて，この辺でtsujimotterはいろいろ混乱してきました．たくさんの拡大が登場してどのような状況を扱っているのかわからなくなってくるからです．私はこういう図を描いて乗り切りました．

f:id:tsujimotter:20170724065633p:plain:w400

　 $\mathcal{O}_{K(E_\pi)}$ の素イデアル $\mathfrak{p}$ での完備化 $\mathcal{O}_{\mathfrak{p}} := \mathcal{O}_{K(E_\pi), \mathfrak{p}}$ とする．次のような２つの群を考えます：

$\mathcal{E} = \{ x\in \mathcal{O}_{K(E_\pi)}^{\times} \mid x \equiv 1 \pmod{\mathfrak{p}} \}$

$\mathcal{U}_{\mathfrak{p}} = \{ x\in \mathcal{O}_{\mathfrak{p}}^{\times} \mid x \equiv 1 \pmod{\mathfrak{p}} \}$

　先に言っておくと， $\mathcal{E}$ は楕円単数のすみかです．この群がどんな群であるかが重要であることを覚えておいてください．

　 $\mathcal{U}_{\mathfrak{p}}$ はおおよそ $K(E_\pi)$ を完備化した体の単数群であるから，定義より $\mathcal{E} \subset \mathcal{U}_{\mathfrak{p}}$ とみなせます．

　 $\mathcal{U}_{\mathfrak{p}}$ は自然に $\mathcal{O}_{\mathfrak{p}}$ -加群で，類体論より LEMMA 1 を使うと次が言えるらしい．

LEMMA 2

$\mathcal{E}$ は $\mathcal{U}_{\mathfrak{p}}^p \subset \mathcal{U}_{\mathfrak{p}}$ に含まれる．

これで楕円単数のすみか $\mathcal{E}$ が，さらに $\mathcal{U}_{\mathfrak{p}}^p$ の中に含まれることがわかりました．

　円単数 $u$ のコールマン写像 $\varphi^{(r)}$ のアナロジーとして，楕円単数 $\Theta_{\mathfrak{p}}$ とコールマン写像の類似物 $\psi^{(r)}$ を考えます．

円単数と楕円単数には，以下のような対応物があります：

円単数	楕円単数
円の $p$ -等分点 $\mu_p$	楕円曲線の $\pi$ -等分点 $E_\pi$
円単数 $u_p$	楕円単数 $\Theta_{\mathfrak{p}}$
ゼータ関数（L関数） $(1-2^r)\zeta(1-r)$	楕円曲線のL関数 $L(r, E)$

　 $\zeta_p$ の代わりに $E$ の $\pi$ -等分点に対するコールマンべき級数（の類似物）をとり，「対数をとって微分する」を行って $\bmod{\mathfrak{p}}$ すると，準同型

$\psi^{(r)} : \mathcal{U}_{\mathfrak{p}} \longrightarrow \mathcal{O}_{\mathfrak{p}} \simeq \mathbb{Z}/(p)$

が構成されます．

　楕円関数の特殊値を用いて構成される楕円単数と呼ばれる $\Theta_{\mathfrak{p}} \in \mathcal{E}$ があり，上の準同型を適用すると以下のように楕円曲線のL関数の特殊値と結びつきます．

f:id:tsujimotter:20170724071720p:plain:w280

　 $r = 1$ として

$\displaystyle \psi^{(1)}(\Theta_{\mathfrak{p}}) \equiv \frac{L(1, E)}{\Omega_E} \pmod{\mathfrak{p}} \tag{13}$

が得られます．ここで，

$\displaystyle \Omega_E = \int_{E(\mathbb{R})}\omega_{E}$

は周期積分と呼ばれるものです．

ゼータ関数の分子に現れる「円周率 $\pi$ 」に対応する数と考えるとよいかと思います．

　 $L(1, E)$ を周期積分 $\Omega_E$ で割った数は

$\displaystyle \frac{L(1, E)}{\Omega_E} \in \mathbb{Q}$

となることが古典的に知られているそうです．

　以上の合同式と LEMMA 2 により

$\displaystyle \frac{L(1, E)}{\Omega_E}$ が $p$ で割り切れる

という結論が得られます．

　ここで $\displaystyle \frac{L(1, E)}{\Omega_E}$ は有理数ですから「 $p$ で割り切れる」という文言については少し注意が必要です．すなわち「 $\frac{a}{b}$ が $p$ で割り切れる」は「 $\frac{a}{b}$ を既約分数で表したときに，分子が $p$ で割り切れる」ことを意味します．上の合同式も「両辺の差を既約分数で表したときに，その分子が $\mathfrak{p}$ で割り切れる」ことを意味します．

　このような合同式のルールについては，前回の記事の触れていますので確認してみてください．
tsujimotter.hatenablog.com

　最後の仕上げです．

　（★）の「 $K$ で完全分解する $p$ 」として無限個の $p$ を考え，それぞれについて以上の議論を行います．

　よく知られているように，虚２次体 $K$ で完全分解する素数 $p$ は無数に存在します．二次体の素イデアル分解法則によって， $K$ の判別式を $d$ として $K$ で完全分解する素数は $\bmod{d}$ の剰余によって定まります．算術級数定理により $dn+b$ 型の素数は無数に存在します．

　また $K$ の類数は１であることから，すべての $p$ は $K$ において一意に素因数分解できるため，完全分解するすべての素数で同様の議論を行うことができます．

　すると $\displaystyle \frac{L(1, E)}{\Omega_E}$ は，無限個の相異なる素数 $p$ によって割り切れることがわかります．

　ここで， $0$ という有理数についての以下の際立った特徴を使います．