今日は「岩澤理論」についてのお話をしたいと思います。
2017年は,岩澤理論の創始者である岩澤健吉先生の 「生誕100周年」 の年にあたります*1。節目の年ということもあって Iwasawa2017 という国際会議が東京で開催されます。
私もこの分野の数学に関心があり,「節目の年である2017年までに」どうにかして理解しようと思い,これまで密かに勉強を続けてきました。
このままでは,岩澤理論を理解できないまま2017年が終わってしまいます。そう思って,2017年の1月より方針を改めることにしました。
毎朝早起きして「1時間限定」で岩澤理論の勉強だけことにしたのです。朝であればどんな予定にも邪魔されることはなく,一定のペースで勉強を進められます。(ついでに早起きして健康的な生活ができる)
これが功を奏して,よい生活リズムのまま約3ヶ月の勉強を続けることができました。
今日はこれまでの勉強の成果を中間発表として報告したいと思います。
私が岩澤理論の勉強に使っている本はこちらです。本記事の内容も,主にこちらの本を参考にしています。
上記の本を「3か月で読み終えること」を目標に勉強を進めてきましたが,ちょうど今月の上旬に読み終えたところです。自分の理解のチェックもかねて,できる限り自分の言葉で解説していきたいと思います。
今回の記事はtsujimotterのまさに勉強中のトピックです。
誤り・勘違い等,多分に含まれるかと思います。証明についても,ブログに書く都合上(そして私の理解の程度によって)流れだけ書いて省略している箇所が多々あります。正確な情報を知りたい方は,ぜひ上記の本を読んでいただけると幸いです。
また,誤りを見つけた際は,tsujimotterの勉強にもなりますし,優しく教えていただけると嬉しいです。
1. 岩澤理論とは
まずは,岩澤理論の全体像について大まかに解説しましょう。
岩澤理論とは 拡大と呼ばれる無限次の代数拡大を考えて,その拡大の言葉で表現できる対象について考える理論です。
拡大のガロア群のなす群環を「岩澤代数」とよび,岩澤代数が作用する「岩澤加群」の性質や,岩澤代数上で定義される「岩澤函数」についての性質を調べます。興味深いことに,この「岩澤加群」と「岩澤函数」にはつながりがあり,両者の関係が具体的に記述できるのです。このような,2つのまったく異なるように見える対象が,実は密接に結びついているという面白さがあり,これが岩澤理論の魅力の一つだと思います。
具体的には,岩澤加群の側に「イデアル類群」という対象があり,岩澤函数の側には「ゼータ関数」という対象があります。19世紀の数学者,クンマーの理論によると「素数 がイデアル類群の位数を割り切ること」と「素数
がゼータ関数の特殊値を割り切ること」は同値であることが知られています。このような「イデアル類群とゼータ関数の間の密接な関係」の背景には,実は岩澤理論があったというわけです。
岩澤理論は,以下に挙げる3本の柱によって成り立っています。
・p進L函数の存在(岩澤函数側)
・岩澤主予想(岩澤加群と岩澤函数を結ぶ)
これら3本の柱を理解することが,岩澤理論の主目的です。
今日は,岩澤理論の入門の入門ということで,一番わかりやすい 「岩澤類数公式」 に絞ってご紹介したいと思います。「p進L函数」や「岩澤主予想」については,類数公式との関連について少しだけ触れたいと思います。
また,一口に岩澤理論といってもさまざまな岩澤理論がありますが,今日はあくまで基本である「イデアル類群の円分岩澤理論」の話にとどめたいと思います。
「○○の岩澤理論」といったときには,上記の3本の柱のそれぞれをセットで考えることになります。
ベーシックな「イデアル類群の円分岩澤理論」の「岩澤主予想」については,MazurとWiles*2が証明しています。理論によっては,岩澤主予想が示されていたりいなかったりもします。
「素数の歌はとんからり」で有名な加藤和也先生は「楕円曲線の岩澤理論」に貢献しています。加藤先生は,岩澤加群側の対象を岩澤函数に結びつけるために,Euler系 をベースとした手法を開発されたのですが,このときのアイデアを「鶴の恩返し」になぞらえて説明しています。 加藤先生の文献には「p進ワープ航法」などのワードが随所に現れてとても楽しげです。
今日のお話は以下の流れで進めたいと思います。
少々(だいぶ?)長いですがお付き合いください!
2. 岩澤類数公式とは
岩澤類数公式は,「イデアル類群」という重要な群の位数(これを「類数」といいます)を表す公式です。
イデアル類群の重要性について,改めて強調するまでもないと思いますが,代数体の研究において「イデアル類群」とりわけ「類数(イデアル類群の位数のこと)」はきわめて重要な情報で,みなが知りたい情報でした。
たとえば,フェルマーの最終定理におけるクンマーの研究を思い出すと,類数の重要性はよくわかります。フェルマーの最終定理は,
を満たす非自明な整数解は, においては存在しないというものでした。この問題は
のままで考えるのではなく,
の整数環まで拡張して考えると良いのでした。
クンマーは,特に一般の素数 について研究しました。円分体
の類数を割り切る
を正則素数,割り切らない素数を非正則素数と分類し,これらの素数を次数に持つ場合における一般論を展開しています。これによって,正則素数の次数に限ってはフェルマーの最終定理が解決したのです。類数が鍵になったのですね。
こうした背景から,類数をよく知りたいというモチベーションがありました。同時に,類数の振る舞いは非常に難しいことも知られていました。
岩澤理論が現れるまで,類数に関する「よい」公式がなかったのです。
このような問題に対して,岩澤先生は1959年の論文で大きな第一歩を踏み出しました。それが「岩澤類数公式」です。
以下のように,無限の拡大体の列を考えて,その 番目の類数を具体的に与える公式を得ることに成功したのです。
十分大きな に対して
によって定まる非負整数
と整数
が存在して
が成り立つ.
いろいろな用語が出てきて戸惑うかと思いますが,これらについてはあとでちゃんと解説します。まずは定理の大枠だけ把握しましょう。
-部分群とは,位数が
のべき乗になる最大部分群のことです。岩澤理論は,このように「特定の
に着目して」その範囲の中で法則を見出していくのが特徴です。
イデアル類群の -部分群だけに着目する法則なので,イデアル類群の全容がわかるわけではないですが,それでもすごいことです。
なにせ,今までよくわからなかった類数について, が十分大きい場合には具体的に計算できてしまうのです。このような公式は,岩澤理論以前には存在しませんでした。
本記事の目的は,この岩澤類数公式の背景を理解し,証明の概略を説明することです。
以下では,先ほど説明しなかった「 拡大」について解説したいと思います。
拡大は,この公式にとどまらず,岩澤理論における中心的な概念です。
3. Zp 拡大
岩澤理論の最大のポイントは,無限の拡大体の列を考えて,その極限をとっているという点です。まずは,その考え方の基礎となる「 拡大(読み方は「ずぃーぴーかくだい」)」について説明しましょう。
3.1. そもそも Zp とは
「 拡大」の前に,
という対象について順を追って説明します。
は素数
に対して定まる「環」です。
を素数としたとき,
は加法について考えると
次の巡回群となります。また,
も
次の巡回群となり,
も
次の巡回群,と無限に巡回群の列を作ることができます。
ここで, として
から元を1つとってきましょう。たとえば,
としましょうか。次に
から
をとってきます。このとき,
であることに注意します。さらに,
から
をとってきます。このときも
が成り立っています。これを無限に続けていくのです。
以上のようすを表したのが以下のイメージ図です。
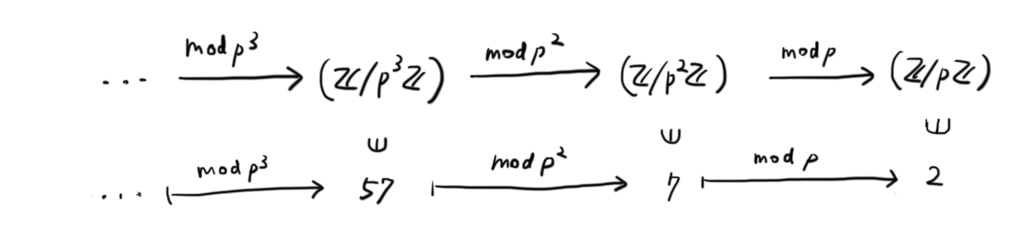
この写像を逆にたどっていき,無限に続く の列で,それぞれ1つずつ数をとっていきます。このような操作を「逆極限」と言います。この逆極限によって得られた数列を一種の「数」とみなすことができるのです。
こうして得られた数をp進整数といいます。通常の整数は有限個の桁しか持ちませんが,p進整数は無限に桁を持つものも存在します。したがって,一般に整数の範囲には収まりません。
p進整数全体の集合は環をなすことが知られています。p進整数全体のなす環をp進整数環といい と表記します。
先ほどの のような数は5進整数環の数,すなわち5進整数といえます。
p進整数環を定式化するためには,逆極限の理解が必要です。
集合 の無限列に対して
なる写像が定義されているとき, に対する無限直積
を考えます。この無限直積全体の集合
を の逆極限といって
という記号で表します。
の例でいうと,
として
なる「
させる写像」を考えれば,
としてp進整数環 を定義できます。
要するに逆極限とは,写像によって数列を数珠つなぎに繋いで,その数列をすべて並べたものを元に持つ集合のことです。「極限」という名称からは「行きつく先」のようなイメージを持ってしまいがちですが,実のところはその途中の元をすべて「同時」に考えていると考えてください。
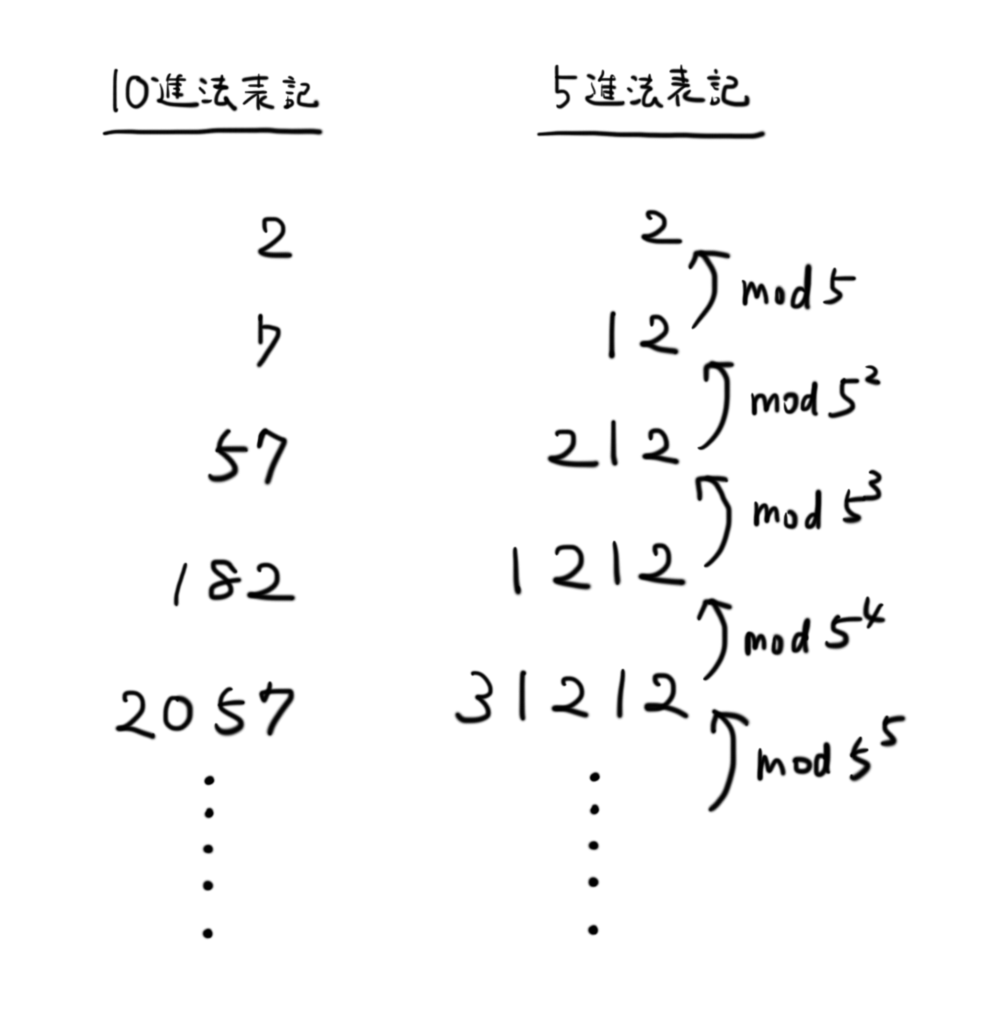
逆極限は慣れるまではなかなかイメージしずらいものですが,p進整数環にはもう少し「直観的な」表現もあります。それは,p進展開です。任意の 進整数は,以下のような
進展開によって表すことができます。
ただし, は
としておきます。これなら,通常の数の形に似ているのでイメージしやすいですね。
先ほどの例では, として
と表せます。
逆極限もp進展開も,以降の議論で使うものなので覚えておいてください。
3.2. Zp 拡大とは
拡大とは,ガロア群が
に同型な拡大のことです。
を基礎体として,まずガロア群が
次の巡回群
になる拡大を
とします。 次にガロア群が
次の巡回群
になる拡大を
とします。こうして拡大を繰り返していって,
次の巡回群
になる拡大
を考え,これを無限に続けます。
こうして得られた拡大の列に対して,無限の極限をとった拡大体
を考え, を
拡大 というのです。
拡大におけるガロア群は
となりますね。

図:Zp拡大のイメージ
上の図のように,高い塔がそびえ立っているようにイメージできるので,別名 タワーとも言います。
私がトランプ大統領くらいのお金持ちになったら,自分のビルに「 タワー」という名前をつけることでしょう。最上階のVIPルームが
です。
このようにいったん
という拡大の列を考えて,最上階である から,中間体
を眺めるのです。
タワーの最上階
に吊るされたゴンドラで,
階(
)まで降りてくるイメージです。

今度は, 拡大
が与えられているとして,中間体
を
の拡大次数が
となるようにとることができます。このような中間体は一意に定まります。
のガロア群
の部分群
を考えます。これは
の元をすべて
乗してできる
の部分群です。この
による商群
を考えると,これは
次の巡回群になります。
ガロア理論の基本定理により,対応する 次の拡大
があり,
は
の固定体になります。
3.3. 円分 Zp 拡大
さて, 拡大の具体例として「円分
拡大」を構成しましょう。あとで述べるように,円分
拡大は,単なる具体例なだけではなく,非常に重要な拡大でもあります。
円分 拡大は,その名からなんとなく想像できるように「円分体」に関連します。
まずは, 次の円分体
におけるガロア群
を考えましょう。ここで,
は
の
乗根全体の集合です。
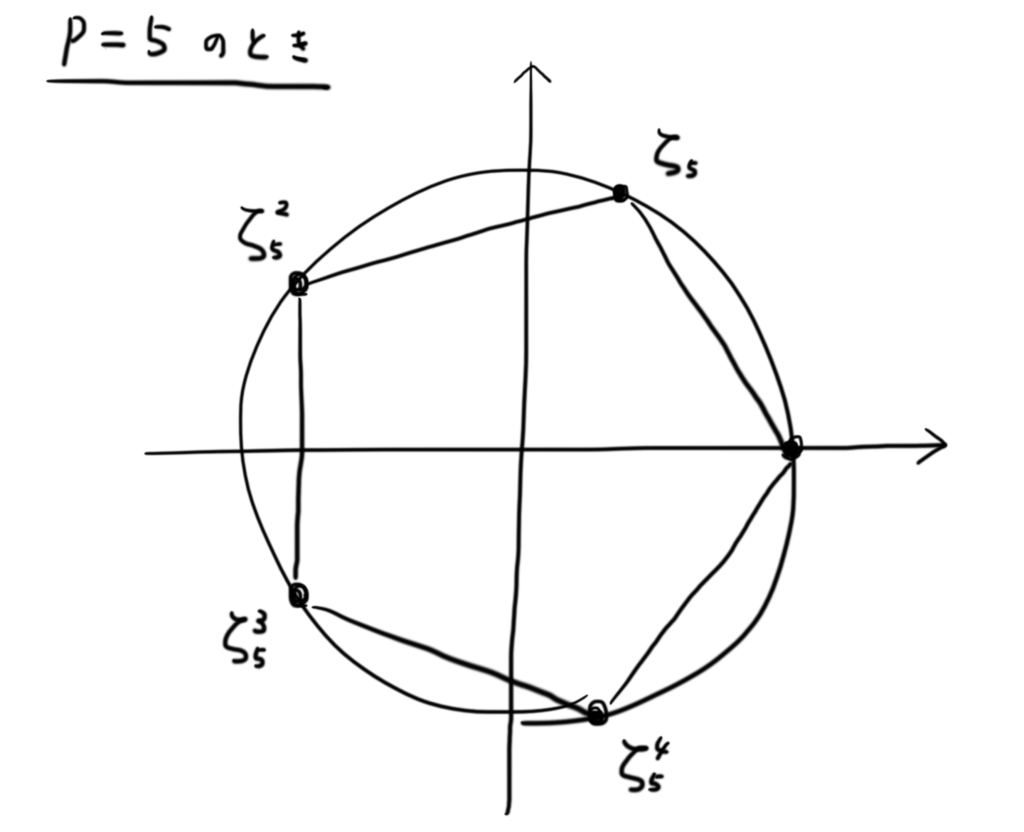
たとえば, のとき,
は以下の図のような単位円上の5等分点全体を
に添加してできる拡大体です。
の任意の元は
を
の原始
乗根として
と書くことができます()。したがって,
の自己同型は
の行き先だけで定まります。
として, によって行き先を定めてあげると,
によって, の自己同型がすべて列挙されたことになります。したがって,これがガロア群
となります。
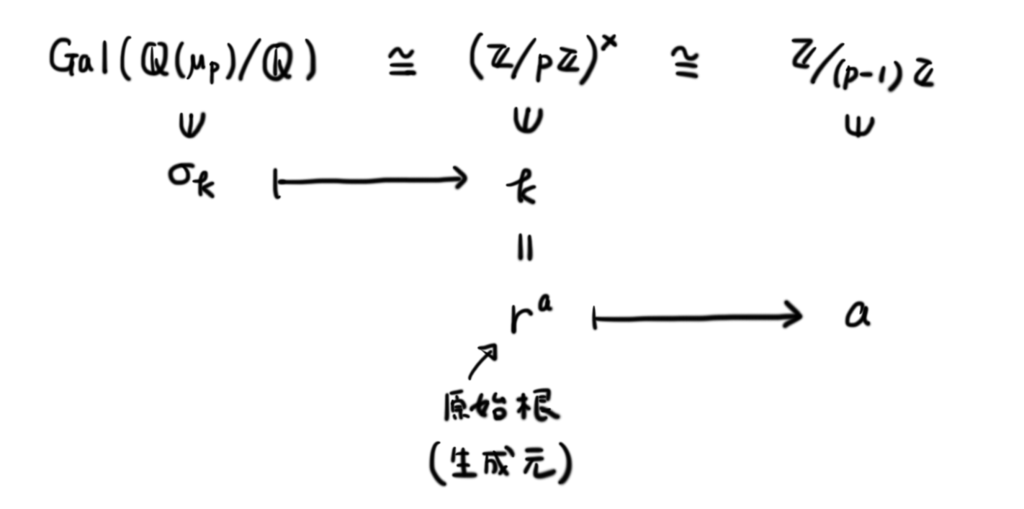
ここで, は
という対応によって, と同型であることが,円分多項式の
上の既約性により示せます。
さらに, は巡回群であることも知られています。いわゆる「原始根定理」です。すなわち,原始根
が存在して,任意の
に対して
となるような
が定まります。この事実により
という対応から, との同型が示せます。
まとめるとこういうことです。
次に, 次の円分体
を考えます。
は
の拡大体になっていることに注意してください。
結論から言うと,このときのガロア群には以下のような同型が知られています。
pn+1 次の円分体においては,ガロア群は単純な巡回群にならず,生成元が2つ必要となります。
は2つの元によって生成できるので,それぞれの元で生成される巡回群の直積として表されるというわけですね。

ガロア群 の部分群で,位数
の元が生成するものを
,位数
の元が生成するものを
としましょう。すると,
と表すことができます。
今までの考察を元に「体の塔」と対応する「群の塔」を描くと以下のようになります。
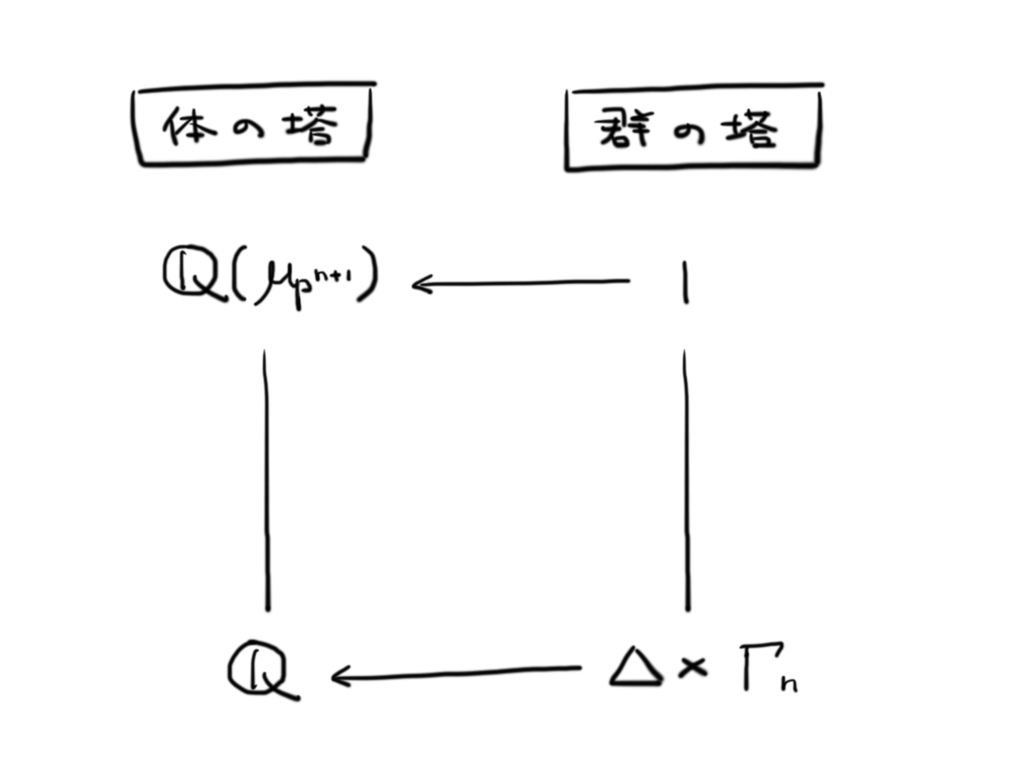
ガロア群 には,部分群
が存在しますから,それぞれに対応する中間体を考えることにしましょう。
の固定する中間体は
となります。一方の
の固定する中間体は(まだ登場していませんでしたが)これを
としましょう。
すると,以下のようなガロア対応が得られます。

注目してもらいたいのは,図の中にある2つの 次の巡回拡大です。
は,ガロア群が
となる
上の
次の巡回拡大
は,ガロア群が
となる
上の
次の巡回拡大
ここでようやく,円分 拡大を定義することができます。
まず, の極限をとります。このとき,
と表記することにしましょう。
上の2つの拡大は, に同型な拡大だったことを思い出すと,
としたときの拡大のガロア群は,
の逆極限をとって
となります。また, は
に同型なので
となり,ガロア群 が
に同型となります。これが 円分
拡大 です。
ここで,「円分」 拡大については,
といった具合に, の文字を付与して区別しましょう。
こうして2つの円分 拡大を作ることができました。まとめておきましょう。
は,ガロア群が
となる
上の円分
拡大
は,ガロア群が
となる
上の円分
拡大
1つめの 上の円分
拡大
は,最も基本となる円分
拡大です。
なぜなら,ほかの代数体 を基礎体としたときの円分
拡大は,
と
の合成体を
とし,
として得られるからです。
実際, の円分
拡大
は,上の実例からわかるように
と
の合成体である
となっていますね。
基礎体を としたときの
拡大は,上に挙げた円分
拡大ただ一つであることが知られています。
また,任意の基礎体 においては,少なくとも1つの
拡大を持ち,そのうち1つの
拡大が円分
拡大です。円分
拡大は,最初のわかりやすい例であり,それゆえ重要な例でもあるのです。
2つの相異なる 拡大の合成体は
拡大となります。こんな調子で,合成体のランクを
拡大の数だけ増やすことができます。レオポルド予想は,そのランクの具体的な大きさを予想しています。
念のため補足すると,レオポルドは「レオポルト・クロネッカー」のことではありません。名前は似ていますが時代がだいぶ異なります。

4. 岩澤代数
を基礎体とする
拡大を
とし,そのガロア群
を考えます。この「ガロア群
の作用を通して,
が作用する対象のことを理解しよう」というのが,岩澤理論の基本的な思想です。
具体的には, を通して
のイデアル類群の
部分
を理解したいと考えるわけです。以下のように考えます。
一方で, はアーベル群なので,整数
が作用します(
の元に
倍が定義できるということです)。ただし,
は位数が
べきの群なので,
(
はある正整数)の元が
に作用すると考えることができます。また,
は,すべての
に対する
の情報を持っていますので,
に
が作用すると考えることができます。
以上から には,
と
の元を形式的に掛け合わせた
が 作用していると考えることができます。このような,
全体の集合は「環」をなすことがわかります。この環を
と表記して群環と呼びます。
このように に対しては,群環
が作用すると考えることができます。
この逆極限をとったものを
として, という記号で表します。この
のことを,「岩澤代数」 といいます。この岩澤代数を通してイデアル類群の
部分を調べることで,岩澤類数公式を示すことができるのです。
今は,イデアル類群を具体的に考えましたが,しばらくはイデアル類群のことは忘れて,岩澤加群が作用する群(これを岩澤加群といいます)を一般的に考えることにします。実は,その方が岩澤類数公式の証明においては,近道なのです。
本節と次節では,この「岩澤代数」と「岩澤加群」の構造について考えたいと思います。
4.1. セールの同型と位相的生成元
岩澤代数 は,いったいどのような構造をもっているのでしょうか。
岩澤理論の発表直後に,岩澤代数 には以下のような同型があることを J.-P. セールが発見しました。
左辺は完備群環,右辺は 係数の形式的べき級数環です。形式的べき級数環は,以下のような「
の元を係数に持つべき級数」全体のなす環です。
完備群環は形式的に定義され実体がよくわかりませんでした。セールの同型のおかげで,岩澤代数を「形式的べき級数」という「よりわかりやすい対象」と同一視して考えることができるのです。
以降では,この「同一視」を積極的に利用して,状況に応じて岩澤代数のことを と言ったり,
と言ったりすることにします。
この同型を考えるにあたっては,位相的生成元という考え方が必要です。
が
次の巡回群
の逆極限でした。したがって,
もある意味では巡回群的な拡大になっているのです。
巡回群であるならば,生成元があるはずです。無限群(かつ位相群)の面倒な点を無視して話を進めると, にも生成元があります。これを位相的生成元といいます。
位相的生成元は便利な存在なので,専用の記号をつけておきましょう。 と書くことにします。
自体は,残念ながら明確に「これ」という式で書くことができないのですが,そういうものが存在するとして話を進めます。
たとえば, としましょう。
は
と同型です。この
の部分は
次の巡回群ですが,これに対応する生成元は
の4つとなります。
次においても同様に生成元は複数存在し,一意に定まりません。逆極限をとった先においても,同様の事情で一意に定まらないので,位相的生成元を考えるときは常に複数の候補の中からどれか1つ選ぶ必要があるのです。
位相的生成元を使って,具体的にどのように対応させるかについて説明します。
まず から位相的生成元
を一つとってきて固定します。この
を
に対応させるのです。この同型写像によって,
の同型が得られます。
逆極限をとる前の を考えます。
は
次の巡回群なので,
に対応する
の元を
とすると,
が得られます。
この式を とおきかえると,
となります。したがって,
によって定義される多項式 を考えて,
を
で割った環を考えると,
のような同型が得られます。この両辺の逆極限をとったものが,セールの同型です。
右辺の逆極限が に一致することについて,適切に議論する必要があります。
以上の対応には,少しだけ注意が必要です。
セールの同型は,位相的生成元 によって定まるわけですが,先に注意したように
は一意に定まりません。また,
の選び方によって,同型の対応関係が異なってしまいます。このような対応を「非標準的な対応」といいます。
一方で,
の場合においても,1の原始 乗根
を1つ考えて同型対応が定義されますが,こちらのケースにおいては,1の原始
乗根
をどのように選んでも同型の対応関係は変わりません。このような対応関係を「標準的な対応」といいます。
岩澤代数における同型を考える際には,非標準的な対応であることを頭に入れた上で,位相的生成元をあらかじめ1つ固定して考える必要があることに注意してください。
4.2. 岩澤代数の構造
岩澤代数の構造をより詳しく理解するために,まず係数環 の環としての構造について考えましょう。
には(
を除けば)ただ一つの素イデアル
があります。そしてこれが極大イデアルです。このように,極大イデアルがただ一つだけであるような環を局所環といいます。ちなみに,
は単項イデアル整域となっていて,すべてのイデアルを
の形で書くことができます。
というイデアルは,
とかける元全体の集合ですが,これらの元はp進展開を用いて
と表せます。したがって, 次以下はすべて
になるような p 進整数全体の集合となります。
当然ですが, は素イデアル
の積によって表すことができますね。
次に について考えましょう。
も同様に局所環となっており,比較的「扱いやすい」環です。
の性質は「p進Weierstrassの準備定理」という定理を使って示すことができます。この定理の系として得られる結論だけ以下にまとめておきましょう。
の極大イデアルは
一つだけ。
の(極大イデアルでも 0 でもない)素イデアルはすべて単項イデアルとなる。これらの素イデアルは,以下の2種類。
の既約な非単数根多項式
によって生成される
のイデアル
の極大イデアルによって生成される
のイデアル
なお, の非単数根多項式
とは,以下の条件を満たす多項式のことです。
はモニック
の係数は
の極大イデアル
以上の事実から,以下のような の素イデアルの昇鎖列が得られます。
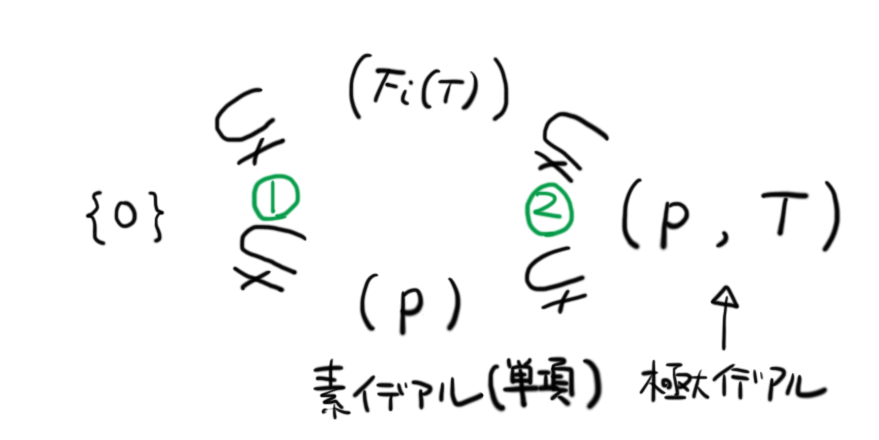
緑色の丸文字で示したとおり,包含記号の個数が なので,クルル次元は
となります。
こんな風に,わかりやすく単項イデアルによって素イデアルが列挙できてしまうのですね。そういう意味で「扱いやすい」環であることがわかります。
この「扱いやすさ」は,以下の節で加群について考えると,より実感できるかと思います。
5. 岩澤加群の構造定理と岩澤不変量
本節では,岩澤加群 の構造について考えたいと思います。
岩澤加群には「岩澤加群の構造定理」によって,わかりやすい構造によって表現されることが知られています。岩澤加群の構造定理は,よく知られた「 加群の構造定理」のアナロジーによって理解することができますので,復習としてそちらを紹介します。
本節の最後では,この構造定理によって定まる,岩澤加群の重要な不変量(岩澤類数公式に関係します)を紹介します。
5.1. 有限生成 Z 加群の構造定理(復習)
まずは,有限生成 加群の構造定理について復習します。
加群とは,
の元が作用する有限生成アーベル群のことです。このような作用を持つことがわかるだけで,実は群の構造がほとんど定まってしまうのです。これが「有限生成
加群の構造定理」です。
一般に,有限生成 加群
に対して,以下のような同型が存在することが知られています:

は自由部分の次元(すなわち,ランク)で,
は
の素イデアルです。ランクが
,つまり自由成分がない加群のことを「ねじれ加群」と呼びます。
注意してもらいたいのは,右辺の構造はすべて の言葉で書かれているということです。作用する環の構造によって(具体的には素イデアルによって)群の構造が表現できてしまうのですね。似たような話はあとでも登場するので覚えておいてください。
5.2. 有限生成岩澤加群の構造定理
次に 加群,すなわち岩澤加群に対して,上記のアナロジーを考えていきましょう。
セールの同型によって,岩澤代数 は形式的べき級数環
と同型になるのでした。以降の議論では,この同型を積極的に利用して,
加群としての
の構造を考えたいと思います。
有限生成 加群の構造定理のアナロジーから,有限生成岩澤加群
は,「
のべき」と「
の素イデアルによる剰余環」の直和によって表現できることが期待できます。そのように表現された
加群を
とすると,以下のような同型が成り立つと期待できるわけです。
※この式は成り立ちません
しかしながら, 加群のときと異なり,この場合は必ずしも同型にはなりません。
実は岩澤加群においては,もう少し緩い「擬同型(同型のような関係)」なら成り立つことが知られています。まずは擬同型を定義することにしましょう。
一般に,準同型写像があったとき,自然に完全系列を得ることができます。

このような完全系列において,左右の加群が自明でなくても「有限」で「擬零加群」であれば,真ん中の関係はゆるく「同型のようなもの」とみなすのです。このような関係を「擬同型」と呼んで, と表記します。
岩澤加群においては, が
と擬同型の関係になり,岩澤加群
を岩澤代数(
)の言葉で表現することができるのです。これが 岩澤加群の構造定理 です。
さて,肝心の ですが,以下のような構造をしています。

非常に重要なので名前をつけておきましょう。 を
の 基本岩澤加群 といいます。
環論的に考えたときに述べたように,岩澤代数は形式的べき級数で表すことができ,比較的わかりやすい構造(極大イデアルは1つ,素イデアルは単項イデアルのみ)を持っているのでしたが,その事実が効いてくるのです。
右辺には「2種類の素イデアル()」しか登場しないことを確認しましょう。
ランクゼロ()のとき「ねじれ加群」といいます。岩澤理論において重要なねじれ加群がしばしば登場しますので,覚えておきましょう。
5.3. 岩澤不変量
岩澤加群の構造定理によって,任意の有限生成な岩澤加群を の言葉によって表すことができました。特に,有限生成ねじれ岩澤加群においては,
の素イデアル
とその指数によって,(擬同型という違いを無視すれば)構造を特定することができるのです。
岩澤加群の構造に関する情報を,端的にまとめたものを 岩澤不変量 といいます。岩澤加群のDNAのような情報ですね。
の2種類の素イデアル
に呼応する形で,
不変量と
不変量という重要な不変量が定義されます。
は岩澤加群
の構造定理に出てきた,素イデアル
に対応する指数で,これらを単純に足し合わせて定義されます。
たとえば,2つの異なるねじれ岩澤加群に対して, 不変量と
不変量の一致から,両者の擬同型を導く手がかりを得ることができます。
もう一つ重要な岩澤不変量として,特性イデアル を定義しましょう。 不変量と
不変量は指数だけを足し合わせたものですが,特性イデアルは素イデアルを指数を加味して掛け合わせたものです。
の特性イデアル
を以下で定義します:
要するに特性イデアルは,既約な多項式をずらずらと並べて掛け合わせてできた多項式によって生成される単項イデアルのことです。ここに岩澤加群の構造がぎっしり詰め込まれているわけですね。
6. 岩澤類数公式の証明の流れ
岩澤類数公式を証明するための準備がようやく整いました。今一度,岩澤類数公式について振り返ってみましょう。
十分大きな に対して
によって定まる非負整数
と整数
が存在して
が成り立つ.
気づいた方もいるかと思いますが,この定理のパラメータである は前節の岩澤不変量そのものです。
はイデアル類群に関連するある有限生成ねじれ岩澤加群
の岩澤不変量になっています。
証明のポイントは, のイデアル類群の
部分
を,岩澤代数
によって分析することです。
ただし,4節で述べたように, は
加群ですので,岩澤代数
が作用する岩澤加群と結び付けてあげる必要があります。
証明の流れは,2段階にわかれます。
- Step 1. イデアル類群
と岩澤加群
を結び付ける
- Step 2. 岩澤加群
の構造定理から
を示す
Step 1. においては,不分岐類体論を使ってイデアル類群を岩澤加群と結びつけます。
Step 2. においては,基本岩澤加群に関する完全系列に対して「蛇の補題」を適用し,最後にp進的な性質を少し使うことで導くことができます。蛇の補題は,tsujimotterのお気に入りの定理なのですが,この蛇の補題を使った証明に感激したことがきっかけでした。
それでは,順を追って解説しましょう。
Step 1. の証明の流れ
第 中間体
のイデアル類群を
とします。
不分岐類体論により, の最大不分岐アーベル拡大
(すなわち
のヒルベルト類体)のガロア群は,イデアル類群と同型であったことを思い出しましょう。つまり,以下が成り立ちます。
tsujimotter.hatenablog.com
ただし,今回関連するのは,イデアル類群 の
-部分
だけです。
ヒルベルト類体を用いるのではなく, の不分岐なアーベル拡大で
べきの拡大次数を持つ最大のものを考えます。これを
の最大不分岐アーベル
べき拡大といい,
と表します。このとき,
と同様の関係が成り立つことが知られています。
左辺のガロア群 が分かれば,イデアル類群の
-部分群のことがわかります。
には
と名前をつけておきましょう。
として極限をとると,同様に
と
が定義できます。また,
の逆極限として
を定義しましょう。
以上の関係を図に描くと次のようになります。

実は は岩澤加群となることがわかります。さらに,後に示すように有限生成ねじれ岩澤加群でもあります。
この岩澤加群 を通して,
を理解しようというのがここでの方針です。タワーの
階をのぞきこむイメージを思い出してください。
議論を簡単にするために,少しだけ技術的な仮定を入れることにします。
の素点で
の上にあるものは唯一つである
における唯一つの
上の素点は,
において完全分岐する
たとえば, の円分
拡大においては,以上の仮定は両方成り立ちます。
これらを仮定すると, は次のように表すことができます。
ガロア群
実際の証明は,不分岐アーベル拡大や惰性群などを使ったかなり技術的に難しい証明になります。大事な部分ではありますが,ここでは省略します。
は
に同型ですから
が得られます。
は,イデアル類群の有限性より有限群です。よって右辺も有限群となります。
さらに岩澤加群の構造定理によって, は有限生成ねじれ岩澤加群であることもわかります。
ここで, として,
と対応させることで,
となりますから,あとは の位数を評価すればよいことになります。
また,以下では と構造定理によって導かれる
という条件も課していきます。
Step 2. の証明の流れ
ここでの方針は, を岩澤基本加群
で表現することです。岩澤基本加群は構造よくわかっているので,これを使って元の個数を具体的に評価できるのです。
上で議論したように, と
は同型にはなりません。したがって,そのずれの分が完全系列における有限の群として現れてきます。これらをどのように扱うかが議論のポイントになります。
実は,完全系列さえ作ってしまえば,それを使って の言葉で
の大きさを表現することができるのです。これには 蛇の補題 を使うことになります。
まずは,岩澤加群の構造定理によって得られた,以下の完全系列からスタートしましょう。
この完全系列のそれぞれに対し 倍する写像を適用します。あとでわかりやすいように,写像の名前を左から順に
としておきましょう。すると,以下のような2本の完全系列が得られます。
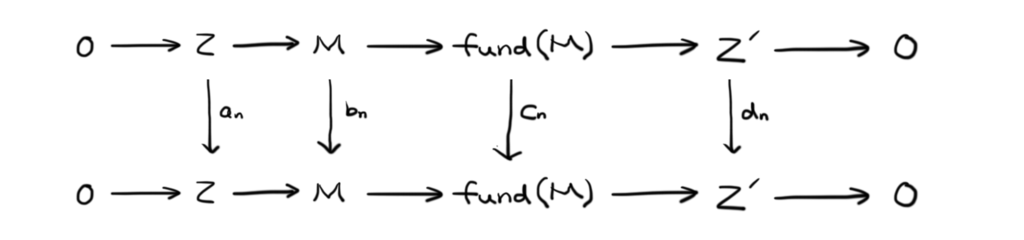
上の2本の完全系列を左右でぶつ切りにして2組の系列に分解します.ぶつ切りにした間には をはさんでおきましょう。
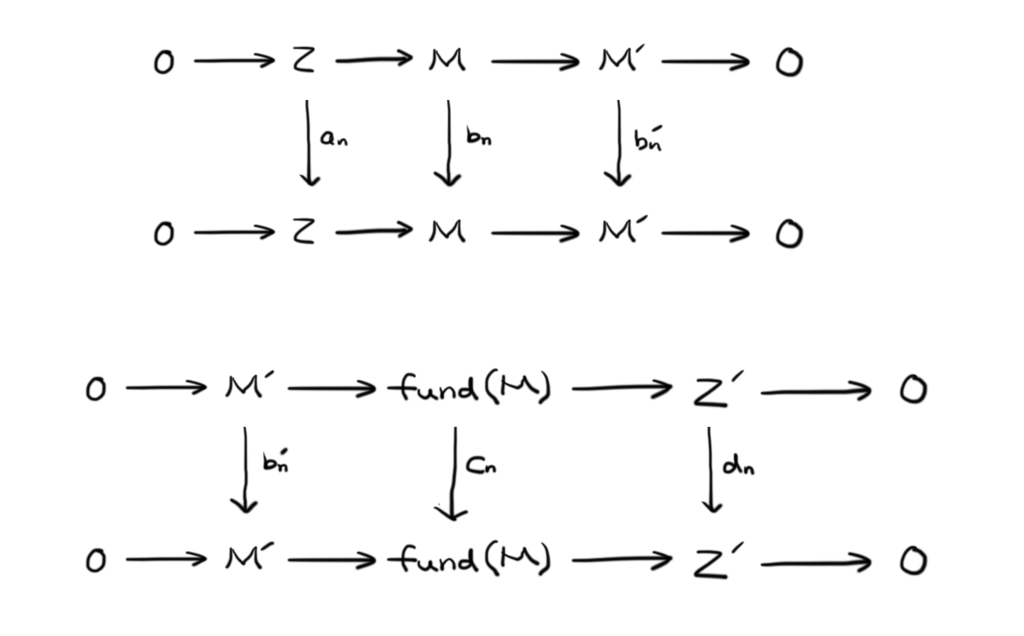
この下の組から処理します。まず,縦方向の写像 それぞれに対して
を考えることで,完全系列を作ることができます。以下の図に薄いグレーで書いておきます。これに蛇の補題を適用すると,

のように,右上の から左下の
に対して準同型写像が入ります(緑色の線です)。蛇のように「うにょーん」と写像がのびていますね。
また,この写像を含む緑色の矢線の系列は完全系列となります。これにて新しい完全系列を得ることができました。
さらに,基本岩澤加群 の特性イデアル
と
は互いに素という前提だったので,
の写像は単射になります。したがって,
です。
以上の考察から,少し短い次の完全系列が得られます:

上の完全系列の要素はすべて有限群となっています。したがって,完全性を元に少しの考察を加えると,以下の式が得られます:
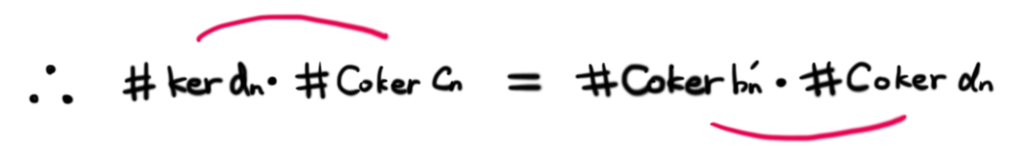
ちょうど,ピンク色の線で結ばれたもの同士の位数を掛け合わせると等式が得られるのですね。
また,以下の図の赤枠で囲った縦の列にも注目してみましょう。
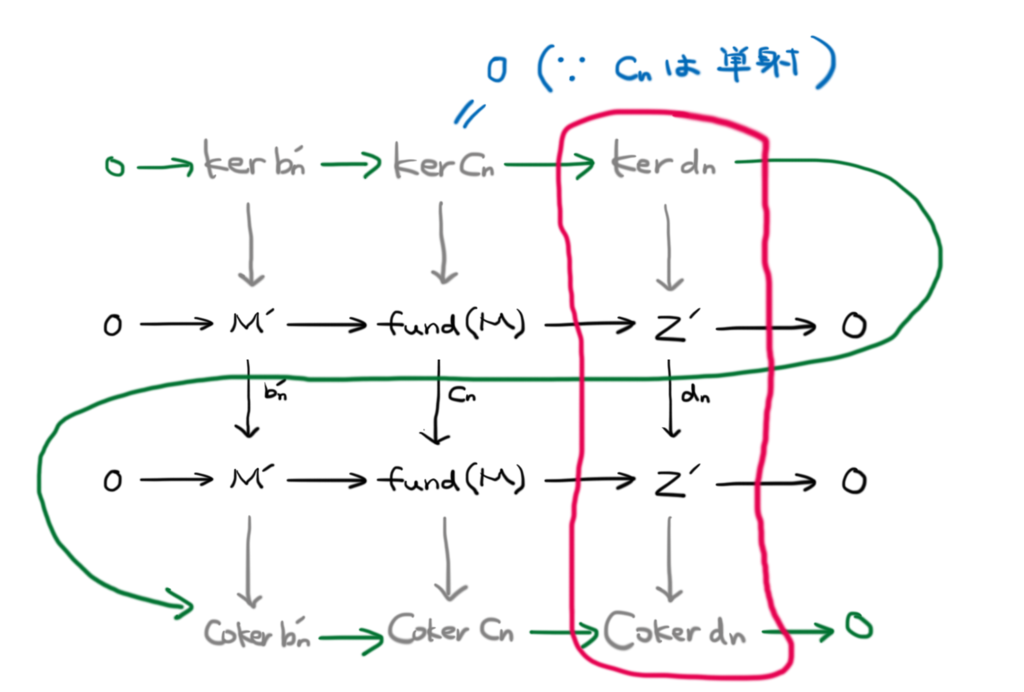
は有限群なので,この完全系列にも同様の法則を考えることができて,
が得られます。結局
が得られました。
同様にもう一方の完全系列の組についても考えてみましょう。
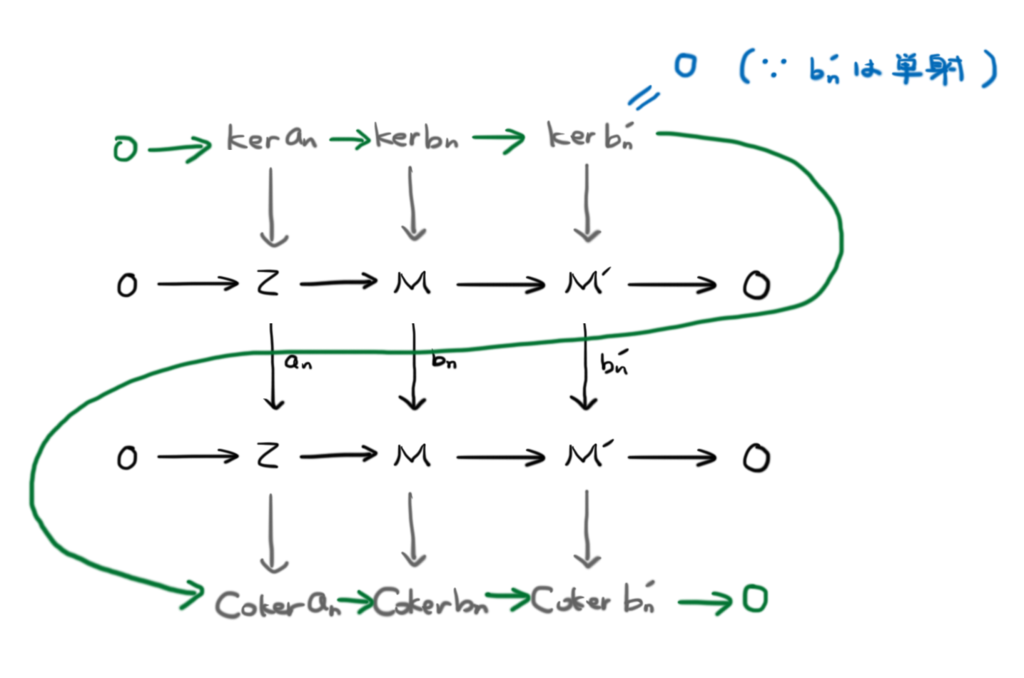
蛇の補題より,緑色で結ばれた完全系列が得られます。また, は単射であることに注意すると,
より,

という完全系列が得られます。これらすべては有限群ですから,以下の式が成り立ちます。
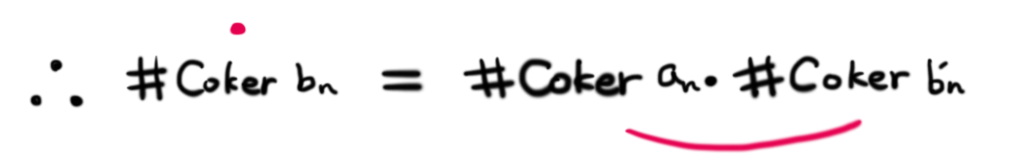
式 を使って
を消去すると,
が得られます。ここで定義より
ですから,
が得られました。
結局,知りたかったのは の位数だったわけですが,これを岩澤基本加群の位数によって表すことができたわけです。

岩澤基本加群は, の2種類の素イデアル
によって定められた成分の直和によって表すことができました。あとは,
に関する部分を
パート,あとは,
に関する部分を
パートとして,それぞれ個別に議論することができます。
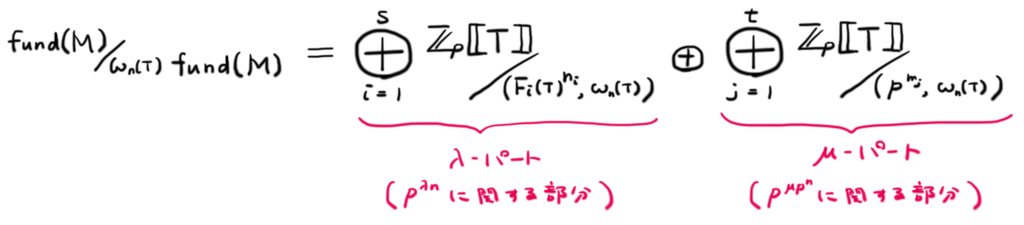
結論から先に言うと, パートの位数は
となり,
を満たす
において
パートの位数は
となります。
の位数を
とすると,
が得られます。
ここで, とおけば,
より岩澤類数公式
が得られます。やりましたね!
パートの具体的な計算は少しややこしくなります。蛇の補題を使って多項式
を一次式に帰着して,円分多項式と p 進数の性質によって計算することができます。
パートの方は簡単なので,片付けてしまいましょう。
の位数を計算すれば十分です。
という同型が得られます。 より,
が得られます。
パート全体の位数はこれらの直和から
となりますが, 不変量の定義から
に一致することがわかります。
7. 具体例の計算
この節では,これまで話してきた内容を,具体例を使って確認してみましょう。
として,
の円分
拡大
を考えます。以下のような状況です。

はアーベル拡大になっていることに注意してください。
このとき, 拡大
の第
中間体は
となりますから,この
のイデアル類群の
部分を
として,岩澤類数公式
を確認しましょう。
要するに( 次)円分体のイデアル類群の位数が,
部分に関してはわかるのです。
具体例として, の場合と
の場合を考えましょう。どちらも参考文献の「数論Ⅱ」に載っている例です。
まずは, から。
のイデアル類群の
部分は
となり,位数は となります。同様に続けていくと,以下の表を得ます。
したがって, としたとき,
として,類数公式が成り立っていますね。
次に の例です。
のイデアル類群の
部分は
となり,位数は となります。同様に続けていくと,以下の表を得ます。
したがって, としたとき,
として,類数公式が成り立っています。
さて,以上の例を見てて気づくことは,いずれの例も となっていることです。 実はこのことは上記の例に限らず,
が有限次アーベル拡大の場合に一般に成り立ちます。
Ferrero-Washingtonの定理を仮定すると, として(
は有限次アーベル拡大),
の第
中間体を
とすると,そのイデアル類群の
部分
の位数は
と表せることがわかります。
今度は,構造定理の視点から の例を観察しましょう。
で,
の極限をとると
です。
対応するイデアル類群は とその逆極限である
となります。これが構造定理の帰結と一致するか確認しましょう。
の岩澤加群としての構造を考えます。岩澤加群
の構造定理より
が成り立ちます。Ferrero-Washingtonの定理から 部分は最初から外しています。
がわかっていると仮定すると,
となり,非単数根多項式 の次数は
となります。ここで,
の非単数根多項式
の定義を思い出しましょう。
の次数 1 の既約な非単数根多項式は
だけです。よって,これを代入して
となって,確かに となっています。
8. まとめと残りの2本柱との関係
本記事では,私がまさに今勉強している「岩澤理論」と,その重要な帰結の一つである「岩澤類数公式」について紹介しました。
今月になってようやく上巻の内容を一通り読み終えたところなのですが,自分の理解のチェックもかねて,自分の言葉でまとめてみることにしました。自分で文章を書いてみたことで,わかったつもりでいた部分に気づくことができて,理解につながりました。
岩澤類数公式は「(代数体の何らかの無限族に対して)イデアル類群を理解する」という難しい問題に対して,初めて答えらしい答えを与えた公式だと思います。そのための方法は,以下に挙げるような非常に面白いものでした。
- 「
拡大(
のべき乗の拡大列すべてをひとまとめにしたような大きな拡大)」を考える
- (イデアル類群そのものを考えるのではなく)岩澤代数
の作用する群(岩澤加群)を一般に考えて,その一般的な構造定理を与える
- 類体論を用いて,岩澤加群の構造定理をイデアル類群に特殊化する
- 蛇の補題を駆使して類数公式を得る
今日は「岩澤類数公式」について解説しましたが,せっかくなのでその先の話についても簡単に触れて終わりにしましょう。
岩澤類数公式の具体例を計算してみると,
という疑問に行き当たると思います。
Ferrero-Washington の定理によって であることがわかるので,
の特性イデアル
がわかれば十分です。
実は,特性イデアルについての情報を教えてくれるのが,p進L函数 と 岩澤主予想 です。
p進L函数とは,岩澤代数の元であって,この元に数論的指標と呼ばれる指標を適用すると 函数の特殊値を取り出せるような特殊な元のことです。
「p進L函数の存在」は,それ自体示すべき重要な定理です。これを認めることで 函数の特殊値の持つ「p進的な性質」を説明することができます。ゼータ関数もL函数の1つなので,ゼータ関数の持つ「p進的な性質」すなわち「クンマーの合同式」を証明することができます。
岩澤主予想は「p進L函数が実はイデアル類群の情報をも持っている」ということを主張する定理です。具体的には,我々が知りたい
したがって,p進L函数を調べることで,岩澤加群の特性イデアルがわかり,岩澤不変量と岩澤類数公式から類数が具体的に計算できるというわけです。
以上が冒頭に述べた「岩澤函数と岩澤加群を結ぶ」ということの意味するところです。この定理から,ゼータ関数と類数におけるクンマーの関係やエルブラン・リベの定理も導くことができます。
非常に面白い内容だと思いますので,そのうち私のブログでも紹介できればいいなと思っています。
落合先生の本を勉強してみての感想ですが,「岩澤主予想という思想をいかに一般化するか」を目標としているだけあって,はるか先を見据えていて率直に言えば「相当難しい」という印象でした。難しい知識を仮定している箇所も多々あって,全部理解できたとはとても言い切れません。
しかしながら,わからないことがありつつも一通り眺めたことによって,岩澤理論における3つの主要な要素(「岩澤類数公式」「p進L函数」「岩澤主予想」)について,「どのように証明されるか」をおおまかにでも知ることができたのが,大変収穫だったと思っています。
引き続き勉強を続けていきたいと思います。
それでは,今日はこの辺で。
参考文献
以下の本の第10章が「岩澤理論」となっています。
上記の本は中古でしか売っていないようなのですが,同じ内容が掲載されたペーパーバック版の本もあるそうです。
訂正:2017/10/28
「数学のたのしみ15 (数学セミナー別冊) 岩澤数学の全貌 その豊穣の世界」の栗原先生の記事を読んで,具体例のところの計算で私の勘違いがあったことに気づきましたので訂正しました。以前のバージョンでは として計算していましたが,正しくは
のようです。


