モンストラス・ムーンシャイン

この記事は明日話したくなる数学豆知識アドベントカレンダーの 23 日目の記事です。（ 22 日目：すごい判別式）

明日話したくなる数学豆知識もいよいよ終わりにさしかかってきました。そろそろ、tsujimotter が一番好きな話をしたいと思っています。

「え？今までのは好きじゃなかったのか？」と思うかもしれませんが、もちろん今までの話も全部好きです。好きじゃなければわざわざ書きません。

それでも、この話は特別気に入っています。（そしてマニアックです。笑）

どれぐらい気に入っているかというと、私のブログのヘッダ画像を見てください。あの茶色い背景に乗った１つの数式。これが今日のテーマの１つである

「j-不変量」

もう１つの主役は

「モンスター群」

これら２つは、まったく異なる分野から生まれた概念です。１つは「モジュラー関数」、もう１つは「群論」。

ところが近年、全く背景の異なるそれらの２つの概念には、世にも奇妙な関係があることがわかりました。この関係につけられた名前が、今回のタイトルにもなった

「モンストラス・ムーンシャイン」

なのです。

あまりに素敵な名前をしているので、夕暮れどきの誰もいない公園で、沈む夕日に向かって叫びたい。それぐらいかっこいい名前です。

そんなモンストラス・ムーンシャインですが、ざっくり言うと「２つの数学的対象の間にある予期せぬ関係性」のことを意味しています。なぜ全く背景が異なる２つの数学的対象に、そんな美しい関係が存在するのか皆目検討もつかない。これは月の光に例えられ、裏にはきっとそれを照らす太陽のような真理が存在するのであろう。

おしゃれな喩えでしょう？

この比喩だけでも、十分面白さを感じてしまいますが、数学的な意味が分かれば、もっと興奮して鼻血がでることでしょう。

というわけで、今日は明日夕日に向かって叫びたくなる数学用語「モンストラス・ムーンシャイン」について解説します。

まずはじめに「j-不変量」、次に「モンスター群」を説明し、最後にそれらをつなぐ「ムーンシャイン」について解説したいと思います。

最初に断っておきますが、tsujimotter は専門の人ではありません。分かる範囲で紹介しますが、誤りも含むかもしれません。証明に至ってはまったくわからないものもあります。雰囲気だけでおもしろがってもらえれば幸いです。

j-不変量

j-不変量 $j(\tau)$ は、モジュラーである複素関数の１つです。いきなり何を言っているんだ、と思ったかもしれませんが、安心してください。以下でちゃんと説明します。

複素関数とは、複素数 $\tau$ を変数にとる関数のことです。余談ですが $\tau$ のようなギリシャ文字は、複素数の変数を表すのによく用いられます。

さて、このブログのヘッダ画像にある式を再掲すると、

《j-不変量の定義》

$\displaystyle \begin{eqnarray} j(\tau)=\frac{1}{q} + 744 &+& 196884q + 21498760q^2 \\ &+& 864299970q^3 + 20245856256q^4 + \cdots \end{eqnarray} \tag{1}$

$\tau$ の関数だと言っておきながら、見た目は $q$ の関数になっています。このように $q$ の多項式として表すことを $q$ 展開と呼びます。 $q$ の定義を考えると、

$\displaystyle q=e^{2\pi i\tau}$

となって、代入すれば確かに $\tau$ の関数となっています。

$q$ に定義式を代入したものを別途表記してもいいのですが、単にややこしくなるだけなので、やめておきましょう。

j-不変量には、非常に面白い性質があります。それは、j-不変量が、次のような等式を満たすということです。

$\displaystyle j\left(\frac{a\tau + b}{c\tau + d}\right) = j(\tau) \tag{2}$

ただし、係数 $a, b, c, d$ はすべて整数で、 $ad - bc = 1$ を満たします。

この意味を即座に理解するのは難しいと思うので、いくつか具体例を示しましょう。

たとえば、 $a=1, b=1, c=0, d=1$ の場合。

$\displaystyle j(\tau + 1) = j(\tau)$

これに似たような関数として、三角関数が挙げられます。三角関数 $f(x) = \cos(2\pi x)$ は $f(x+1) = f(x)$ のように平行移動させても関数の形を変えません。つまり、 j-不変量は、三角関数のような周期的な性質を持っているということです。

もう１つ例を挙げると、こんな等式も含まれます。 $a=0, b=-1, c=1, d=0$ の場合。

$\displaystyle j\left(\frac{-1}{\tau}\right) = j(\tau)$

これらは一例です。このようなあらゆる変換を用いて変数を変換したとしても、関数の形が元に戻るという訳です。

関数に変換をかけても元に戻るという性質は、いわゆる「対称性」という言葉で表現されますが、要するに j-不変量は

「むちゃくちゃたくさんの対称性をもった関数」

というわけです。

ある関数 $f$ がこのような性質を持っている、ということを「 $f$ はモジュラーである」といいます。モジュラーであるような関数は、ほかにいくつも考えられるのですが、ちょっとした自然な条件を付けることで、一意に、すなわち j-不変量１つに定める事が出来るそうです。

モンスター群

モンスター群について説明するためには、まず「有限群」について基本的な事を話さないといけません。少々遠回りにはなりますが、「有限群」とは何かを話した後、「単純群」を説明し、さらに「有限単純群の分類定理」を説明して、ようやく「モンスター群」について話しができます。

以下、ちょっと長い解説になります。「モンスター群」とは、位数がとんでもない大きさを持った「有限単純群」のことです。という解説を聞いて意味を理解できる人はこの項目を読む必要はありません。

有限群とは

群とは何か。ここから説明しましょう。群の定義は次の Wikipedia にも書いてあります。

群 (数学) - Wikipedia

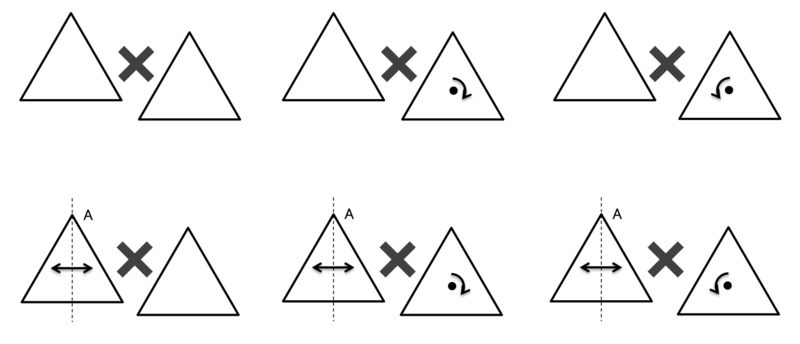
よくわからないと思うので、具体的な例を挙げるのがいいと思うのです。

f:id:tsujimotter:20141223133859p:plain:w200

図のような正三角形を回転させたり、ひっくり返したりして、見た目がまったくかわらないように元に戻す操作を考えましょう。

全部列挙すると、以下の６パターンになります。

この場合「何も動かさない操作」も１つの操作とみなします。この６つの要素をまとめて「正三角形を元に戻す操作によって構成される群」です。

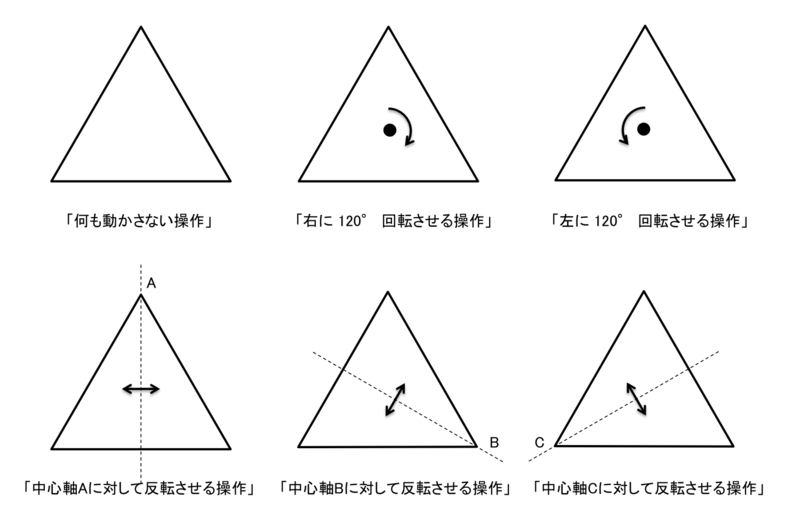
パターンの総数のことを「位数」といいます。つまり、この「正三角形を元に戻す操作によって構成される群」の位数は「６」である、ということです。無限の位数を持つ群も考えられるのですが、今回は有限の位数の群だけを扱います。これが

「有限群」

です。

もう１つ、まったく同じ位数「６」を持つ群を挙げてみましょう。

f:id:tsujimotter:20141223134459p:plain:w200

図は参考文献より引用

上のヒトデ型の図形は、1/6 回転, 2/6 回転, 3/6 回転, 4/6 回転, 5/6回転, そして何もしない操作という計 6つの操作に対して元に戻る図形です。

この群は、「1/6 回転の操作」たった一つから構成されます。つまり、「1/6 回転の操作」を繰り返し行う事で、６つすべての操作が表現できるのです。このような群のことを「巡回群」と呼びます。ヒトデの群は「位数６の巡回群」です。

同様にヒトデの足を３つにすれば「位数３の巡回群」がつくれますし、足を２つにすれば「位数２の巡回群」もつくれます。

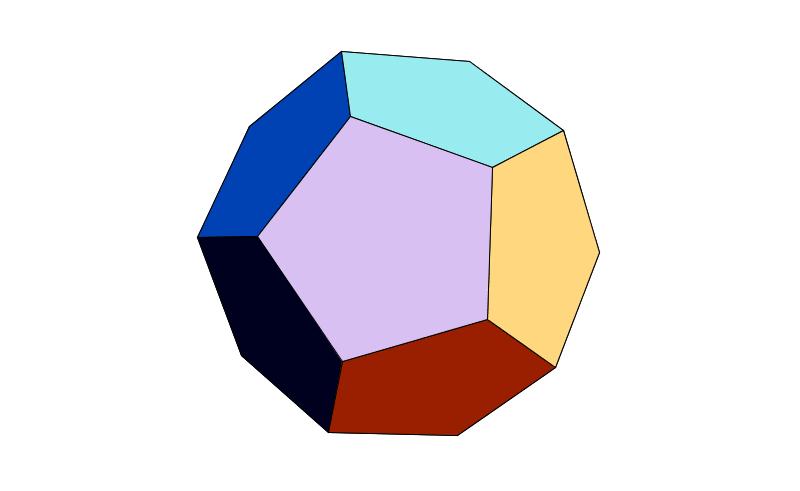
すべての群が二次元平面上で定義できるわけではありません。三次元空間でないと定義できないような複雑な群も存在します。たとえば、「正十二面体を元に戻す操作」によって構成される位数 60 の群が存在します。

f:id:tsujimotter:20141223142856j:plain:w360

もう１点、部分群について触れておきましょう。
「正三角形を元に戻す操作の群」の中には、次のようなより小さな群が隠されています。「正三角形を 1/3 回転させる操作の群」です。

このような、群の中に隠されたより小さな群のことを「部分群」と呼びます。

ところで、この部分群ですが、操作だけをみると「３本足のヒトデの群（つまり、位数３の巡回群）」と同じものであることがわかります。このような、見た目は異なるけど、操作としては等価な群のことを「同型な群」といいます。群の理論においては、同型な群は同じものと見なします。
したがって、正三角形の群は、部分群として「位数３の巡回群」を持つ、といえます。

次に進むための準備はこの辺にしておきましょう。

正規部分群と単純群

正規部分群とは、部分群の中でも、特に都合のよい性質を持った部分群のことです。正規部分群は、群の「割り算」が出来る群のことです。

割り算の前に「かけ算」から。

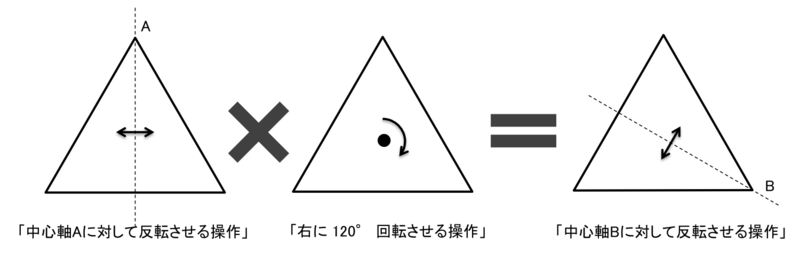
群の要素である操作を２つとってきて、それらを組み合わせて用いることで別の操作に一致させることができます。これを「かけ算」と定義しましょう。

正三角形の群で考えると、次のような「かけ算」が考えられます。

要素だけでなく、部分群同士でも「かけ算」を行うことが出来ます。

たとえば、正三角形の群のすべての要素は、次のように「かけ算」を用いて表現し直す事が出来ます。

f:id:tsujimotter:20141223143057p:plain:w460

これを、まるで因数分解のようにまとめることができます。

f:id:tsujimotter:20141223143106p:plain:w460

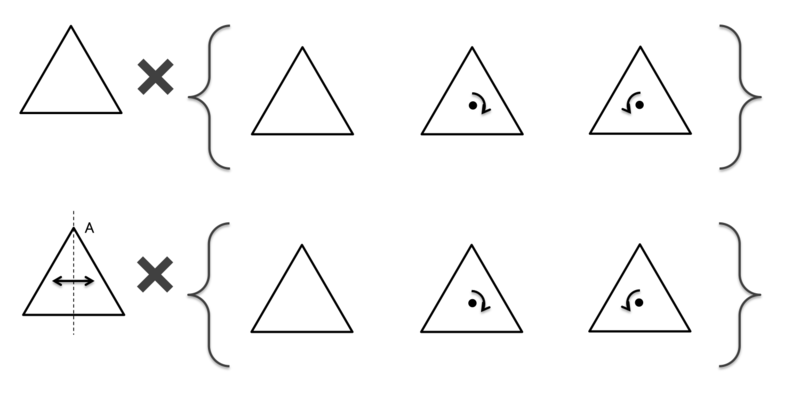
このことは、括弧の中にある「正三角形の回転の操作の群（位数３の巡回群）」で全体の群を「割り算」すると、左にあるような二つの操作の集合が得られる、と表現する事が出来ます。そして、この残った２つの操作はそれ自体、群をなします。具体的には「位数２の巡回群」です。

これを「正規部分群」という言葉を使って表現し直すと、こうなります。

「正三角形を元に戻す操作の群」を正規部分群である「位数３の巡回群」で割ると、「位数２の巡回群」が得られる。

このように、部分群で「割り算」を行ったときに、その商も群となるような "都合のいい" 部分群のことを「正規部分群」というわけです。（本来はもっと厳密に定義されるのですが、今はイメージだけで勘弁してほしい。）

どんな群でも「何もしない操作をただ１つ持つ群」という群と自分自身を、正規部分群として持ちます。が、これらは明らかなので「自明な群」と呼びます。

すると有限群には、「自明な群」以外に、正規部分群を持つものもあれば、持たないものも存在します。たとえば、先ほどの正三角形の群は、正規部分群として「位数３の巡回群」を持ちますし、素数位数の巡回群はすべて「自明な群」以外に正規部分群を持ちません。上で例に挙げた「正十二面体による位数６０の群」も、「自明な群」以外に正規部分群を持ちません。

このように、これ以上、正規部分群で割ることのできない群のことを

「単純群」

といいます。

ここで重要な事は、どんな有限群も単純群に分解できる、ということです。これは、数の素因数分解でたとえると分かりやすいかもしれません。単純群は、素因数分解でいう素数みたいなものです。

どの辺が似ているのかどうか、素数と見比べてみましょう。

《素数の定義》
1 と自分自身以外に約数を持たない数
《単純群の定義》
位数 1 の群と自分自身以外に正規部分群を持たない群

「群の素因数分解」は、もっと直接的に、数の素因数分解に対応づけて説明することも出来ます。

たとえば、先ほどの「正三角形を元に戻す操作によって構成される群」は位数６ですが、「位数３の巡回群」で割り切る事ができて、その商は「位数２の巡回群」でした。このことは、次の割り算とまったく同じ事を言っています。

$6 \div 3 = 2$

数の素因数分解と異なるのは、単純群の位数が必ずしも素数ではないということです。位数 60 の単純群があれば、それは分解できません。あくまで単純群に分解できるということに注意してください。

有限単純群の分類定理とモンスター

どんな有限群もすべて単純群に分解できる、という事実はなかなかにインパクトがあります。つまり、有限群について知りたいと思ったら、単純群をすべて調べればよいのです。

ここで、単純群は果たして無限に存在するのか、ということが気になってきます。単純群が有限のパターンしか存在せず、しらみつぶしに単純群を調べることができれば便利です。

その問いに「単純群は有限のパターンしか存在しない」と答えたのが

「有限単純群の分類定理」

です。この定理によって、すべての単純群が明らかになりました。つまり、すべての単純群を載せたカタログが作れるという事です。

コンウェイという数学者は、この単純群のカタログを一冊の本としてまとめました。その名も "Atlas of Finite Groups (有限群の地図帳)"。有限群のすべてが詰まった 250 ページの本です。

Atlas of Finite Groups: Maximal Subgroups and Ordinary Characters for Simple Groups

作者:Conway, John Horton,Curtis, Robert T.,Norton, Susan Potter,Parker, R. A.,Wilson, R. A.
発売日: 1986/01/02
メディア: リング製本

この地図帳の中に、コンウェイたちは「とんでもない数の位数を持つような群」を書き加えなければなりませんでした。その群の位数は次のものです。

$\begin{eqnarray} &&2^{46} · 3^{20} · 5^9 · 7^6 · 11^2 · 13^3 · 17 · 19 · 23 · 29 · 31 · 41 · 47 · 59 · 71 \\ &&= 808017424794512875886459904961710757005754368000000000 \end{eqnarray}$

だいたい $8\times 10^{53}$ 程度の大きさを持っています。この途方もない大きさの群を、数学者たちは

「モンスター群」

と呼んでいます。なぜ彼らは、このようなモンスターを見つける事が出来たのか。今の tsujimotter にはそれについて解説する力はありませんが、とにかく存在することは証明されているのです。

さて、このモンスター群、見てみたいと思いませんか？私は見てみたい。
でも残念ながら、先に述べた理由により、複雑過ぎて二次元平面上で表現することは出来ません。群論の専門家であるマーカス・デュ・ソートイ博士によると、奇妙に入り組んだ雪の結晶のような形をしている、とのことですが、私にはよくわかりません。

さて、モンスター群を数学的に表現しようと思うと、二次元平面どころか、三次元空間でも不可能です。では、一体いくつ次元があれば表現できるかというと・・・

それは、196883 次元です。

ようやく本題にやってきました。勘の良い人は先ほどの数字を見て気づいてしまったかもしれません。

ものすごくたくさんの対称性を持ったモジュラー関数である「 j-不変量」。この q展開は次のようなものでした。

$\displaystyle \begin{eqnarray} j(\tau)=\frac{1}{q} + 744 &+& 196884q + 21498760q^2 \\ &+& 864299970q^3 + 20245856256q^4 + \cdots \end{eqnarray} \tag{1}$

そして、次に説明をしたとんでもない位数を持つ「モンスター群」。これを表現するための最小の次元数は、

196883

でした。

気づきましたでしょうか？
そう、q展開の $q$ の一次の係数が、なんとモンスター群の次元 196883 に、1 を加えた値になっているのです。当然ですが、どちらの数字も適当に決めた数ではありません。まったく異なる背景に基づいて決められた数です。この２つの数が、1 を加えただけで完全に一致してしまう！

なんということでしょう！！

さらに、すごいことが起きます。
先ほどの 196883 次元は、モンスターが表現できる最小の次元でしたが、もっと大きな次元でも存在できる事が知られています。その次元数を小さいものから列挙していくと、

$196883, 21296876, 842609326, 18538750076, 19360062527, 293553734298, \cdots$

これらを順に、

$r_2, r_3, r_4, r_5, r_6, r_7, \cdots$

とおいて、さらに

$r_1 = 1$

としておきましょう。

すると、q展開の係数が、次のように $r_n$ についての簡単な線形結合で表せるのです。

$\begin{eqnarray} 1 &=& r_1 \\ 196884 &=& r_1 + r_2 \\ 21498760 &=& r_1 + r_2 + r_3 \\ 864299970 &=& 2r_1 + 2r_2 + r_3 + r_4 \\ 20245856256 &=& 3r_1 + 3r_2 + r_3 + 2r_4 + 2r_5 \end{eqnarray}$

この関係は、この先もずっと続いていきますが、どの関係も簡単な線形結合です！

これが「モンストラス・ムーンシャイン」です！

f:id:tsujimotter:20141223125358j:plain:w320

いやあ、興奮しますね！！！

おわりに

以上をまとめると、ムーンシャインとは

むちゃくちゃたくさんの対称性を持った、モジュラー関数 $j(\tau)$
とんでもない数の位数を持ちながら、実は単純群であるモンスター群

この２つの全く異なる数学的対象の間をまたぐ、神秘的な関係だったのです。

いかがでしょう。ムーンシャインについて叫びたくなってきましたか？笑

一応、この記事は「明日叫びたくなる数学用語」ではなく「明日話したくなる数学豆知識」なので、以下に豆知識的な話を入れておきましょう。

j-不変量とモンスターの間の予期せぬ関係は、1978年にジョン・マッカイによってはじめて示唆されました。その後、コンウェイによって「ムーンシャイン予想」と命名されました。

「ムーンシャイン」という名は、太陽と月の関係のような深遠な意味のほかにも、「馬鹿げた」「きちがいじみている」といった意味も含んでいるそうです。当時、このとんでもない関係を目の当たりにした数学者の心境が読み取れますね。

ムーンシャイン予想は、まさに「モンスター」と「j-不変量」の間にある「予期せぬ関係」を具体的に表しているものといえます。もし、この背後にある真実を解き明かす事が出来れば、数学の真理に到達できそうな予感も感じさせます。

ちなみに、ムーンシャイン予想は、1992年にコンウェイの弟子であるリチャード・ボーチャーズによって証明されました。ボーチャーズはこの証明によってフィールズ賞を受賞しています。コンウェイによると、ボーチャーズによって証明はされたものの、この２つの対象についての謎は依然として残っているとのことです。

ボーチャーズの証明、知りたいですよね。知ったかぶってもしょうがないので白状すると、tsujimotter はまったく読んだ事がありません。たぶん、きっと読んだとしてもチンプンカンプンでしょう。勉強して、いつかは理解したいですね。

よくわからない、難しいけれど、何かそこに奥深いものが潜んでいそうで、惹かれてしまう。それがムーンシャインなのでした。

明日は taketo1024 さんによる「複素数を作ろう」です。私はこの方の同名のスライドを見たのですが、非常に面白い話でした。明日も楽しみです！
「明日話したくなる数学豆知識」はいよいよ、明後日で最終日です。最後は、私 tsujimotter が、これまでの数学豆知識を振り返りたいと思います。

「j-不変量」はこんなところにも登場します。ということで過去記事を貼っておきます。

参考文献

モンスターとムーンシャインについて、群論の専門家マーカス・デュ・ソートイ先生によって書かれた本です。単に数学的に面白いだけでなく、ストーリー仕立てになっていて非常に読みやすい・・・といいつつ、実はちゃんと全部読んでなかったことに気づいて、今慌てて読んでいます。新たな発見があれば書き加えていくかもしれません。やっぱり面白い。

シンメトリーの地図帳 (新潮クレスト・ブックス)

作者:マーカス・デュ・ソートイ
発売日: 2010/02/26
メディア: 単行本

2014年12月24日追記：
この本を読んでみて、モンスター群を実際に構成したグライスさんが不憫に思えてきました。「自分の名前を新しい群につけてやるんだ」とがんばって構成したのに、それが既に「モンスター」という変なあだ名をつけられていて、しかもそれがまたインパクトがあるのです。かわいそうなので、今度から「モンスター群」のことを「フィッシャー・グライス　モンスター」あるいは、彼が名付けた「フレンドリー・ジャイアント」と呼んであげようかな。

おまけ

関連動画（？）です。数学科の学生が作った群に関するオリジナルソング。
"Finite Simple Group of Order Two" とは「位数２の有限単純群」ということ。
今回の話が理解できれば、タイトルの意味ぐらいはわかるはず。笑
ちなみに、"The Klein Four" は、たぶん「クラインの四元群」を意識しているのだと思います。