ヒルベルトの第12問題（類体の構成問題）に進展があったらしい

センセーショナルな数学関連のニュースが飛び交っている昨今ですが、私にとって特に注目したい情報が入ってきました。それがヒルベルトの第12問題に関する進展です。

「総実体上のヒルベルトの第12問題を解いた」というプレプリントが 3/4付でarXivに投稿されたのです。次のリンクから参照できます：

Samit Dasgupta, Mahesh Kakde
Brumer-Stark Units and Hilbert's 12th Problem
[2103.02516] Brumer-Stark Units and Hilbert's 12th Problem

後で詳しく説明しますが、まずは簡単に概略を述べます。

「虚2次体 $K$ 上の類体を構成することができるか」という数学上の問題は「クロネッカーの青春の夢」として知られていました。

1900年に発表された「ヒルベルトの23の問題」の中で、虚2次体 $K$ を代数体 $K$ に一般化した上で取り上げられました。これが「第12問題」です。ヒルベルトの23の問題の中で、現在も未解決の問題は、第8問題・第12問題・第16問題・第23問題の4つであり、第12問題はそのうちの一つとして知られています。

$K$ として有理数体を選んだ場合はクロネッカーとウェーバーにより実現され、虚2次体の場合も後に解決されました。CM体の場合についても結果が出ているそうです。（私は理解できていません。）

それ以外の体については解決の見通しは立っていなかったものと思われますが（違っていたらすみません）、今回 $K$ が総実体の場合に解決した（とされる）プレプリントが公開されたということです。

とても魅力的なニュースだと思うのですが、なかなかに専門的な話です。背景を知らないと上記の数行を理解するのは難しいかと思います。

そこで、今回は「類体の構成問題」というテーマで、この問題の背景をご紹介したいと思います。論文自体の内容を紹介するのは難しいので、あくまで私のわかる範囲で、その背景に絞って紹介したいと思います。

注意１：
今回のものは「プレプリント」ですので、正しさが保証されているわけではないという点に注意したいと思います。

学術論文というのは、一般に論文誌に投稿され、数名の査読者によって内容が十分に精査されてから論文誌として出版されます。この過程によって、内容の正しさが一定程度保証されるわけですね。もちろん、査読をクリアしたからといって証明が正しいと保証されているわけではなく、出版後もさまざまな研究者によって検証されていくわけです。

今回のものは、論文誌に投稿前（あるいは査読中）の原稿を事前公表する「プレプリント」と呼ばれるものであり、まだ査読が入っていない原稿です。したがって、（著者が万全のチェックをした上で出していることは仮定してよいとは思いますが）十分に正しさが保証されたものとはいえません。内容の正しさは、あくまで読者自身が確認することが前提というわけですね。

そのため、まだプレプリントの段階の内容を紹介する際には、その点を十分に配慮する必要があると考えています。この記事をご覧になった方で、この件について発信される場合は、上記の点について十分配慮願えると幸いです。

注意２：
著者のtsujimotterは、該当分野の研究者ではありません。あくまで、ただの一数学ファンが勉強して書いたというものですので、専門的な観点からここで書かれた内容の真偽を保証するものではありません。その点はあらかじめご了承ください。

また、間違っている点の指摘は、私自身の勉強にもなりますので歓迎します。

目次：

1. 類体のおさらいとアーベル拡大

2. ℚ上のアーベル拡大（クロネッカー・ウェーバーの定理）

3. 虚2次体上のアーベル拡大（クロネッカーの青春の夢）

4. ヒルベルトの第12問題

5. 類体の構成問題のその後の進展

6. 今回のプレプリントについて

1. 類体のおさらいとアーベル拡大

今回のテーマは、類体の構成問題です。まずは類体という概念についておさらいしたいと思います。

とはいえ、最初から最後まで説明するのも大変ですので、以前書いたこちらの記事で「類体」と「類体論」についての雰囲気を感じていただけると、今回の内容をよりよく理解できると思います。
tsujimotter.hatenablog.com

上の記事で説明したことを、かいつまんでまとめるとこういうことです。

まず土台となる舞台として有理数体 $\mathbb{Q}$ を考えます。そして、有理数体の素数 $p$ を考えます。
（正確にいうと $\mathbb{Q}$ の整数環 $\mathbb{Z}$ の素数を考えるということです。）

素数 $p$ は、定義より有理数体（の整数環）の中ではこれ以上分解できません。しかしながら、 $\mathbb{Q}$ より大きな体 $L$ に持ち上げると、分解することもあれば、分解しないこともあります。この法則（分解法則）はどのように表すことができるのか、というのが前回のテーマでした。

たとえば、素数 $p$ を $\mathbb{Q}(i)$ に持ち上げたときの、 $p$ の分解法則は $\bmod{4}$ で定まります。実際、次のような法則が成り立ちます：

$p \equiv 1 \pmod{4}$ である素数は $\mathbb{Q}(i)$ において２つの素数の積に分解する　（例： $13 = (3+2i)(3-2i)$ ）
$p \equiv 3 \pmod{4}$ である素数は $\mathbb{Q}(i)$ において素数の積に分解されない　（例： $7$ は $\mathbb{Q}(i)$ で分解されない）

f:id:tsujimotter:20210306175142p:plain:w300

$\mathbb{Q}(i)$ における分解法則は、 $\mathbb{Q}(i)/\mathbb{Q}$ のガロア群 $(\mathbb{Z}/4\mathbb{Z})^\times$ によって規定されている、と捉えられます。つまり

$(\mathbb{Z}/4\mathbb{Z})^\times = \{ \overline{1}, \; \overline{3} \}$

の部分群である $H = \{ \overline{1} \}$ を考えて、素数が $H$ に属するときに限り $\mathbb{Q}(i)/\mathbb{Q}$ で完全分解する、というように解釈できます。

f:id:tsujimotter:20210306180438p:plain:w300

他の拡大の例も与えましょう。 $\mathbb{Q}(\sqrt{-7})$ に持ち上げて完全分解される素数は、 $(\mathbb{Z}/7\mathbb{Z})^\times$ の部分群 $H = \{\overline{1}, \overline{2}, \overline{4}\}$ に属する素数のみであることが示されます。

また、円分体 $\mathbb{Q}(\zeta_m)$ で完全分解される素数は、 $(\mathbb{Z}/m\mathbb{Z})^\times$ の部分群 $H = \{ \overline{1} \}$ に属する素数のみです。

こんな風に $(\mathbb{Z}/m\mathbb{Z})^\times$ の部分群 $H$ によって分解法則が与えられるような $\mathbb{Q}$ 上の拡大体のことを、 $\mathbb{Q}$ 上の類体といいます。

f:id:tsujimotter:20210306175304p:plain:w300

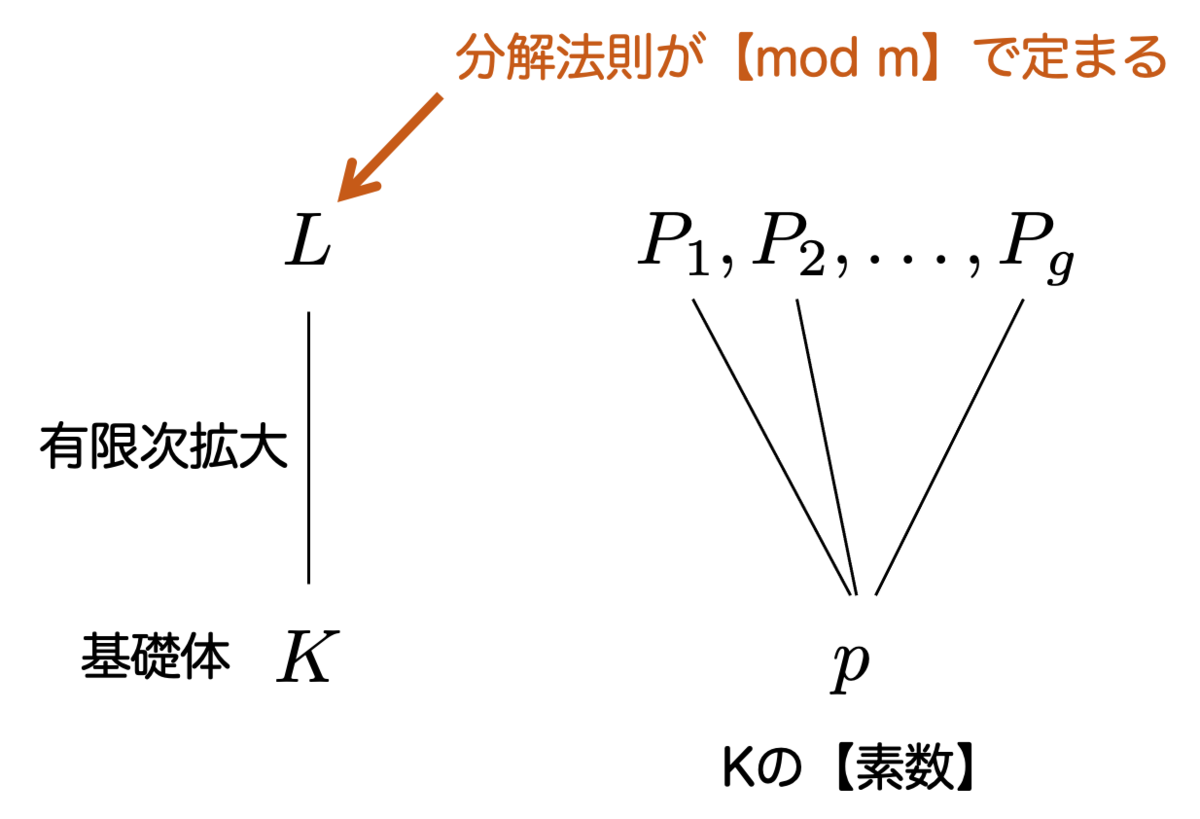
この「〇〇上の」という部分が最も大事です。下にある〇〇という体に対して、その「素数」を上の体××に持ち上げられたときに $\bmod{m}$ で分解法則が定まるかどうかが知りたいわけですね。

以下では「下の体（こういう体を基礎体といいます）」を、有理数体から別の代数体に置き換えて考えることをしたいと思います。

代数体とは、 $\mathbb{Q}$ 上の有限次拡大体のことです。

任意の代数体 $K$ に対して、 $K$ 上の（有限次）拡大体を $L$ とします。 $K$ の【素数】を $L$ に持ち上げるときに、その分解法則が【 $\bmod{m}$ で】定まるかを考えたいというわけです。

f:id:tsujimotter:20210306175218p:plain:w300

基礎体を任意の代数体 $K$ に取り替えたことで、【】で書いた部分について若干の修正が必要になります。

【素数】の部分を【素イデアル】に、【 $\bmod{m}$ で】の部分を、整数 $m$ ではなく「整因子 $\mathfrak{m}$ 」を用いて【 $\bmod{\mathfrak{m}}$ で】と修正する必要があります。

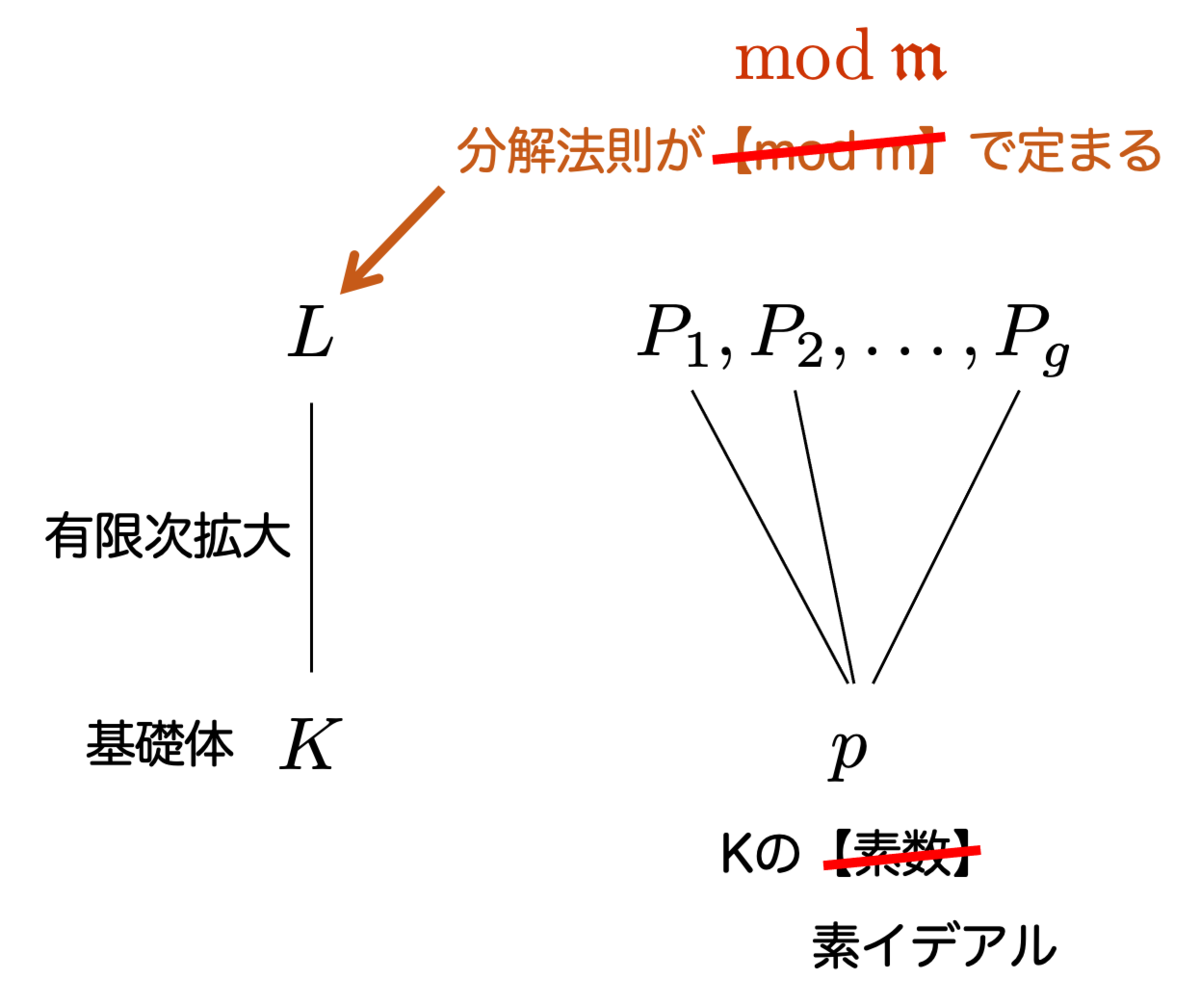
f:id:tsujimotter:20210306175237p:plain:w300

このように修正した上で、「 $K$ のイデアルを $\bmod{\mathfrak{m}}$ で分類した群」を考えます。これを $K$ の $\bmod{\mathfrak{m}}$ の合同イデアル類群 $\operatorname{Cl}_K(\mathfrak{m})$ といいます。

$K = \mathbb{Q}$ のときの $(\mathbb{Z}/m\mathbb{Z})^\times$ に対応する群だと思ってもらえればOKです。

$K$ の素イデアルの分解法則が $\operatorname{Cl}_K(\mathfrak{m})$ の部分群 $H$ によって規定されるような $K$ 上の拡大体のことを、 $K$ 上の類体というわけです。

f:id:tsujimotter:20210306175336p:plain:w320

さて、類体論における存在定理が主張しているのは、こういうことです。

$\operatorname{Cl}_K(\mathfrak{m})$ の任意の部分群 $H$ に対して、 $K$ 上の類体が存在する

類体の存在は分かったとして、類体がいったいどんな拡大体なのだろうか、という問題は残ります。ここで重要なキーワードはアーベル拡大です。 $L/K$ がアーベル拡大とは、そのガロア群がアーベル群（可換群）であることを言います。

類体の定義から、そのガロア群がアーベル群であることがわかるので、類体は $K$ 上のアーベル拡大であることがわかります。類体論はその逆も示していて、なんと $K$ 上の任意のアーベル拡大は類体だというのです。

$K$ 上の類体はアーベル拡大であり、 $K$ 上のアーベル拡大は類体である

何か禅問答のような話ですね。アーベル拡大とはすなわち類体（つまり素イデアル分解の法則がよくわかる拡大体）であったということが、類体論によって示されたというわけです。

2. ℚ上のアーベル拡大（クロネッカー・ウェーバーの定理）

類体論によって、代数体 $K$ 上のアーベル拡大に大いに興味が湧いたことと思います。

次に気になってくるのは、アーベル拡大にはいったいどのようなものがあるのか、ということです。

類体論は、アーベル拡大の具体的な形がどうなるかについては何も教えてくれません。さらに踏み込んでいく必要があり、ここに未解決問題が生じる余地があります。

まずは、現在よく分かっている状況として、基礎体を有理数体 $\mathbb{Q}$ として考えましょう。 $\mathbb{Q}$ 上のアーベル拡大にはどのようなものがあるでしょうか。

実は円分体がすべてであるというのが結論です。

まず、正の整数 $m$ を考えて $\bmod{m}$ の類体を考えることにします。このとき、 $\bmod{m}$ の類体において最大のものを考えれば、その部分体としてすべての類体（つまりアーベル拡大）を考えたことになります。 $\bmod{m}$ の類体の中で最大のものをRay類体といいます。

クロネッカーとウェーバーは、次のような事実を示しました：

定理（クロネッカー・ウェーバー）

$\mathbb{Q}$ 上の任意のアーベル拡大 $K/\mathbb{Q}$ に対し、 $K$ を含む円分体 $\mathbb{Q}(\zeta_m)$ が存在する

すなわち、 $\mathbb{Q}$ 上の $\bmod{m}$ のRay類体が円分体 $\mathbb{Q}(\zeta_m)$ であることを示したというわけですね。

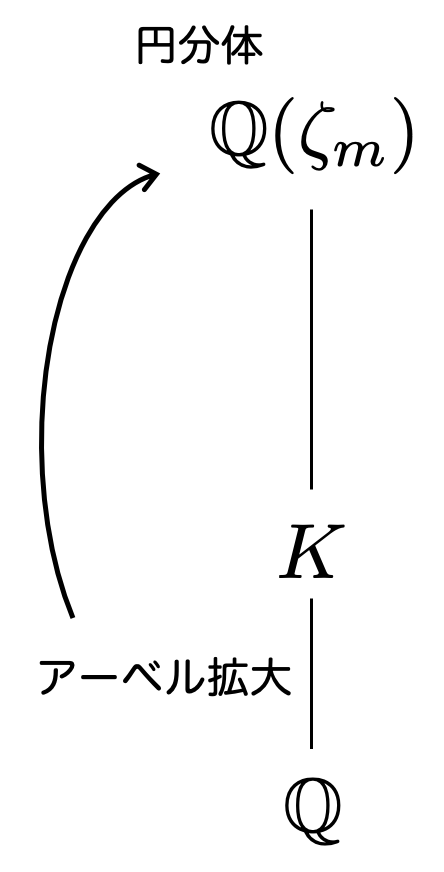
f:id:tsujimotter:20210306181144p:plain:w110

改めて強調すると、円分体の部分体で $\mathbb{Q}$ 上のアーベル拡大は尽くされていたというわけです。円分体すげー。

また、 $\mathbb{Q}$ 上の任意のアーベル拡大を合成したものを $\mathbb{Q}^{\text{ab}}$ とします。これを $\mathbb{Q}$ 上の最大アーベル拡大と言います。この $\mathbb{Q}^{\text{ab}}$ の部分体として、 $\mathbb{Q}$ 上の任意のアーベル拡大がすべて網羅されるわけですね。

このとき

$\displaystyle \mathbb{Q}^{\text{ab}} = \bigcup_{m} \mathbb{Q}(\zeta_m)$

が成り立つというのが、クロネッカーウェーバーの定理の言い換えです。 $\bigcup_{m} \mathbb{Q}(\zeta_m)$ は、任意の $m$ に対する $\mathbb{Q}(\zeta_m)$ すべての合成体です。

左辺の部分体として $\mathbb{Q}$ 上の有限次の部分体 $K$ をとります。すると、右辺より $K$ が円分体の有限合併に含まれることがわかります。円分体の有限合併はある円分体に含まれるので、これにより元々のクロネッカー・ウェーバーが導かれます。

円分体は $\mathbb{Q}$ に $1$ の原始 $m$ 乗根 $\zeta_m$ を添加した体でした。 $\zeta_m$ は円を $m$ 等分点ということですが、 $\zeta_m$ は、複素数平面上では円を $m$ 等分した点だと思うことができます。

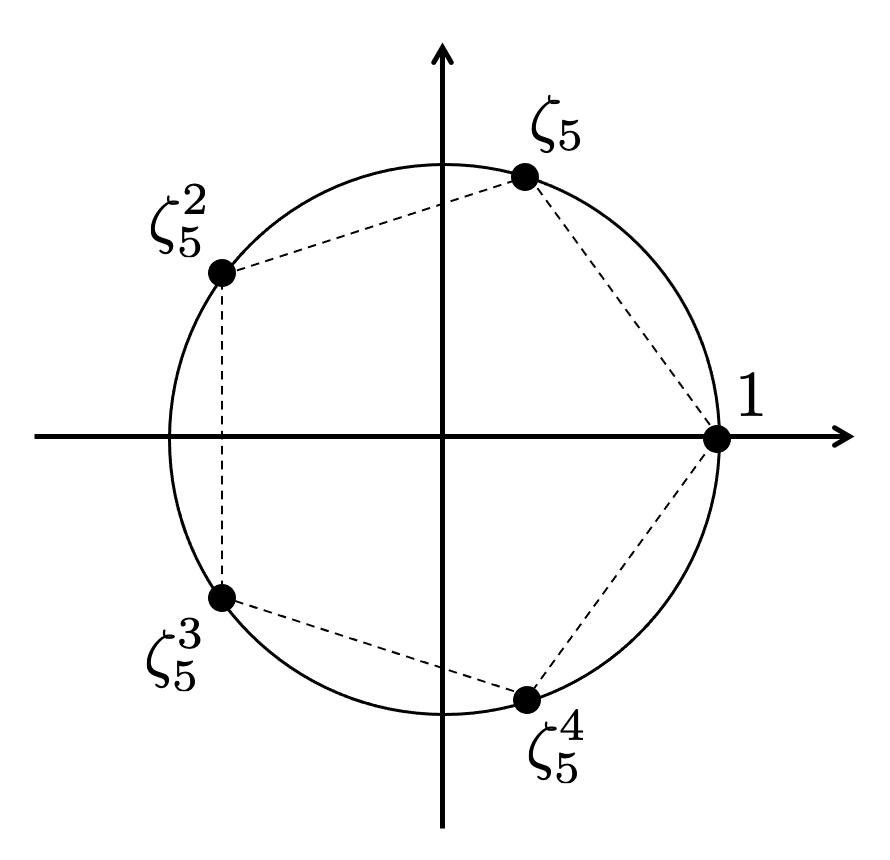
f:id:tsujimotter:20210306175407p:plain:w220

これは幾何的な見方ですが、関数を使った見方もできます。1の原始 $m$ 乗根 $\zeta_m$ は、指数関数を用いて

$\displaystyle \zeta_m = \exp\left( \frac{2\pi i}{m} \right)$

のように表すことができます。そこで $f(x) = \exp(2\pi i x)$ という関数を考えると

$\displaystyle \zeta_m = f\left(\frac{1}{m}\right)$

と書くことができます。

要するに、指数関数 $f(x)$ の特殊値を添加することで円分体が生成できるということですね。この部分体として、 $\mathbb{Q}$ 上の任意のアーベル拡大が尽くされるということです。

3. 虚2次体上のアーベル拡大（クロネッカーの青春の夢）

$\mathbb{Q}$ 上のアーベル拡大を具体的に表すことができたので、今度は一般的な代数体 $K$ 上のアーベル拡大を考えたくなります。

クロネッカーは、 $K$ を特に虚2次体としたとき、円の等分点の代わりに虚数乗法を持つ楕円曲線を使って同様の法則が成り立つのではと予想しました。

2次体とは、 $\mathbb{Q}$ に $\sqrt{m}$ （ $m$ は平方数ではない整数）を添加して得られる体のことです。特に、 $m$ が正の整数のとき実2次体、 $m$ が負の整数のとき虚2次体といいます。たとえば $\mathbb{Q}(\sqrt{-1})$ や $\mathbb{Q}(\sqrt{-7})$ は虚2次体の例となっています。

この予想はクロネッカーの青春の夢といって、現在では虚数乗法論と類体論を駆使して証明されています。予想の名前がかっこいいので、名前だけ知っている人は結構多いのではないかと思います。これがあの有名な青春の夢だったというわけです。

結局、次のような定理が成り立ちます。

定理（クロネッカーの青春の夢）

虚2次体 $K$ に虚数乗法を持つ楕円曲線 $E$ を考える。 $E$ の $j$ 不変量を $j(E)$ とし、 $E$ の $m$ 等分点全体の集合を $E[m]$ とする。このとき、 $K$ の最大アーベル拡大は

$\displaystyle K^{\text{ab}} = \bigcup_{m} K(j(E), h(E[m]) )$

と表せる。ここで $h$ はウェーバー関数。

ウェーバー関数というのが出てきましたが、これは「だいたい $E[m]$ の $x$ 座標をとってくる関数」だと思っていただければと思います。

$\mathbb{Q}$ のときと同じように考えると、虚2次体 $K$ 上の任意のアーベル拡大 $L/K$ に対して、 $L$ を含むような体 $K(j(E), h(E[m]) )$ が存在するということですね。

f:id:tsujimotter:20210306204935p:plain:w330

青春の夢は $\mathbb{Q}$ 上のときと同じように「関数の特殊値の問題」としても定式化できます。

楕円曲線 $E$ は、ある複素数 $\tau$ を使って $E_{\tau}$ のようにパラメータ化することができます。これによって、 $j(E)$ は $j(\tau)$ と表すことができます。また、 $E$ の点の $x$ 座標は、別の複素数 $z$ に対するワイエルシュトラスのペー関数 $\wp(z; \tau)$ として表すことができます。したがって、 $j(\tau)$ および $\wp(z; \tau)$ の特殊値を添加することで、 $K$ 上の最大アーベル拡大が得られるというわけですね。

また、 $K$ 上のアーベル拡大 $L/K$ に対して、 $L$ を含むような拡大体を関数 $j(\tau), \wp(z; \tau)$ の特殊値によって与えられるというわけですが、使用する関数 $j(\tau), \wp(z; \tau)$ は $L/K$ によらないというのがポイントです。

$\mathbb{Q}$ 上のときには、その関数は指数関数 $\exp(x)$ だったのを思い出しましょう。この関数の代わりに、虚2次体 $K$ の場合は $j(\tau), \wp(z; \tau)$ が使われるということですね。

クロネッカー自身が想定していたのは、関数を用いた問題設定だと思います。実際、クロネッカーが友人デデキントに宛てた手紙の中で次のように述べています。

Es handelt sich um meinen liebsten Jugendtraum, nämlich um den Nachweis, dass die Abel ’schen Gleichungen mit Quadratwurzeln rationaler Zahlen durch die Transformations- Gleichungen elliptischer Functionen mit singularen Moduln grade so erschöpft werden, wie die ganzzahligen Abel’schen Gleichungen durch die Kreisteilungsgleichungen.（それは我が愛する青春の夢です。つまり、整係数アーベル方程式が円分方程式によって尽くされるのと同様に、有理数の平方根を係数に含むアーベル方程式が特異母数を持つ楕円函数の変換方程式で尽くされることの証明です。）
— レオポルト・クロネッカー、クロネッカー全集第5巻, p. 455; リヒャルト・デーデキントへの手紙 (1880年) より（Wikipediaより引用）

4. ヒルベルトの第12問題

クロネッカーを引き継いで、さらに一般化させた問題を世界に提示したのがヒルベルトです。

1900年にパリで開催された第2回国際数学者会議において、有名なヒルベルトの23の問題が提示されました。これから100年の間に解かれべき問題として、特に重要とされるものを幅広い分野から集めたリストとなっています。その第12問題として、クロネッカーの青春の夢の拡張が選ばれたのです。

クロネッカーの定理を、有理数体または虚2次体の代わりに、任意の代数体を取った場合に拡張すること。私はこの問題を、数および函数の、すべての理論の中で最も深く最も重要なものの一つと考える。この問題は、多くの側面から近づき得るように見える。（Wikipediaより引用）

すなわち、任意の代数体に対して、その上の最大アーベル拡大が（指数関数や楕円関数のような）適当な関数の特殊値として実現できるかという問題です。

類体論の用語を使って言い換えるならば、任意の代数体 $K$ に対して、 $K$ 上のray類体を適当な関数の特殊値として構成できるかという問題ですね。このような問題を一般に類体の構成問題といいます。

なお、ヒルベルトの23の問題の中で、2021年3月現在も未解決のまま残った問題は、第8問題・第12問題・第16問題・第23問題の4つだけです。第12問題はそのうちの一つとなっています。ちなみに、第8問題はあの有名な「リーマン予想」です。

5. 類体の構成問題のその後の進展

以上で問題設定を説明し終わりましたが、類体の構成問題はその後どこまで進展したのでしょうか。

クロネッカー・ウェーバーの定理は、 $\mathbb{Q}$ 上の類体の構成問題を解決するものでした。これはヒルベルトの第12問題以前の結果であり、これがきっかけとなり青春の夢が予想されたのでした。

その後、クロネッカーの青春の夢、すなわち虚2次体 $K$ 上の類体の構成問題が、虚数乗法論を用いて解決したのは上で述べた通りです。

虚2次体が解決したということで、次は実2次体だと思うかもしれません。しかし、そう簡単な話ではないようです。実際、実2次体の類体を構成するような一般的結果は存在しなかったように思われます。

これについては本当に私が知らないだけの可能性もあります。その場合は大変申し訳ありません。

一方で、CM体と呼ばれる、虚2次体を一般化するような基礎体に対しては、志村・谷山の研究（アーベル多様体の虚数乗法論）による結果があります。

私の理解不足により、CM体について完全に解決しているかどうかについては、ちゃんと調べてないので私は断言することができません。

そんな中、実2次体を一般化した総実体に対して、その上の類体が構成されたというのが今回のニュースです。

ここで重要なキーワードとして総実体と CM体について説明しておきます。

代数体 $K$ に対して、複素数体 $\mathbb{C}$ への環準同型 $\phi \colon K \to \mathbb{C}$ を考えます。一般に、環から体への環準同型は単射になることから、これは $\mathbb{C}$ への埋め込みを与えます。

この埋め込みによって $K$ を $\mathbb{C}$ に埋め込んだ $\phi(K)$ を考えます。任意の $\phi$ に対して $\phi(K)$ が $\mathbb{R}$ に含まれるとき、 $K$ は総実体であるといいます。

たとえば、実2次体 $K = \mathbb{Q}(\sqrt{2})$ を考えると、環準同型 $\phi \colon K \to \mathbb{C}$ は

$\phi(a+b\sqrt{2}) = a + b\,\phi(\sqrt{2})$

なので $\sqrt{2}$ の行き先だけで決まります。 $\phi(\sqrt{2})^2 = \phi(2) = 2$ より、 $\sqrt{2}$ の行き先は $\sqrt{2}$ か $-\sqrt{2}$ のいずれかになります。よって、埋め込みはこの2種類だけです。

いずれの埋め込みも $\phi( \mathbb{Q}(\sqrt{2}) ) \subset \mathbb{R}$ となりますので、 $\mathbb{Q}(\sqrt{2})$ は総実体となります。

他の例としては、たとえば $\mathbb{Q}$ は総実体です。円分体 $\mathbb{Q}(\zeta_m)$ の部分体である $\mathbb{Q}(\zeta_m + \zeta_m^{-1})$ も総実体です。

$\mathbb{Q}(\sqrt[3]{2})$ は総実体ではありません。 $\omega$ を1の原始3乗根として、 $\phi(\sqrt[3]{2}) = \omega \sqrt[3]{2}$ によって定まる埋め込み $\phi \colon \mathbb{Q}(\sqrt[3]{2}) \to \mathbb{C}$ が存在しますが、 $\phi( \mathbb{Q}(\sqrt[3]{2}) ) \not\subset \mathbb{R}$ となるからです。

一方、任意の埋め込みが $\mathbb{R}$ に含まれないような体（言い換えると、 $\mathbb{R}$ に含まれる埋め込みが存在しない体）を総虚な体と言います。もちろん、総実でも総虚でもない代数体は存在します。

総虚な体であって、特に総実体の2次拡大になっているような体を CM体といいます。CM体の例として分かりやすいのは虚2次体です。

たとえば $\mathbb{Q}(\sqrt{-1})$ を考えます。 $\mathbb{Q}(\sqrt{-1})$ から $\mathbb{C}$ への埋め込みは、① $\sqrt{-1}$ を $\sqrt{-1}$ に映すもの、② $\sqrt{-1}$ を $-\sqrt{-1}$ に映すものの２つあります。どちらも、 $\mathbb{R}$ 内に含まれませんので、総虚な体です。

また、 $\mathbb{Q}$ は総実体より、 $\mathbb{Q}(\sqrt{-1})$ は総実体上の2次拡大であるような総虚な体なので、CM体というわけですね。

ほかにも、円分体 $\mathbb{Q}(\zeta_m)$ は総虚な体であり、総実体 $\mathbb{Q}(\zeta_m + \zeta_m^{-1})$ の2次拡大なのでCM体です。このような体を含んだクラスを考えているわけですね。

だんだん複雑になってきたかと思いますので、以上の関係を図にまとめておきましょう：

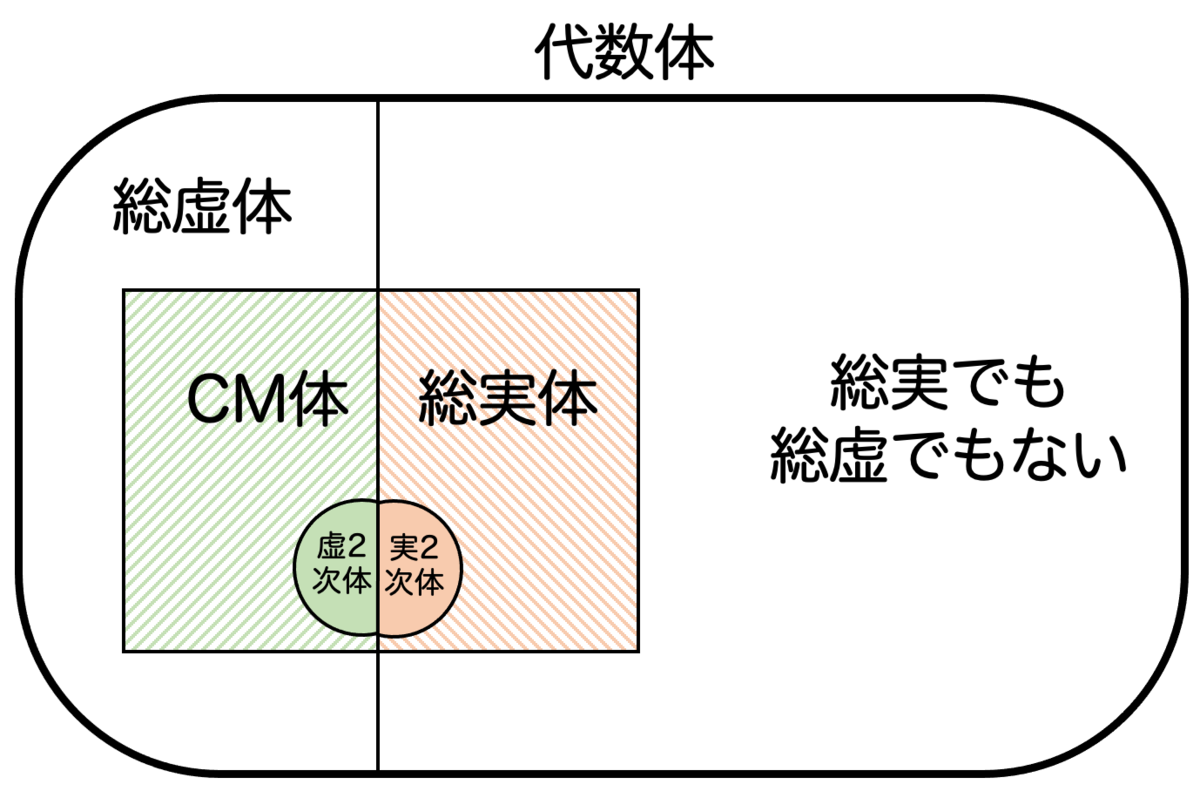
f:id:tsujimotter:20210306232426p:plain:w360

（大きさはテキトーなので、あくまで包含関係に着目してください。）

さて、類体の構成問題に戻ると、基礎体が虚2次体の場合は楕円曲線の虚数乗法論によって解決されました。それを一般化したCM体においては、楕円曲線の一般化であるアーベル多様体の虚数乗法論によって成果がありました。

そんなわけで、CM体の方は虚数乗法論が使えたわけですが、（実2次体を含む）総実体においてはそうはいかなかったというわけですね。

なお、代数体に限らなければ、最大アーベル拡大が構成されている体もあるようです（加藤・黒川・斎藤「数論1」に書いてありました）。

たとえば、有限体上の1変数関数体の場合には、Drinfeld加群と呼ばれるものの等分点を使って、局所体においてはLubin-Tate理論において形式群（formal group）の等分点を用いて最大アーベル拡大を構成できることが知られているそうです。

6. 今回のプレプリントについて

そこで、今回のDasguptaさんのプレプリントなのですが、なんと基礎体が総実体の場合の類体を構成できたという結果のようなのです。

もちろん内容は非常に難しく、私にはまったく理解できません。なので真偽も判定できるレベルにないのですが、本当ならすごいことだと思います。

不正確であることを承知の上で、あえてかいつまんで説明しようと試みます。

どうやらスターク予想というものが関係しているようです。「類数公式のすごいやつ」みたいな予想だと認識しています。

参考：類数公式は以下の記事で解説しています：
tsujimotter.hatenablog.com

スターク予想は、どうもデデキントゼータ関数のテイラー展開の係数と、スターク単数（Stark unit）と呼ばれるものとの関係を表す予想なのだそうです。今回のプレプリントで考えているのは、特に Brumer–Stark conjectureと呼ばれるものだそうです。（私にはこれらの研究の差異を説明する力はありません。）

また、Wikipediaに書いてありましたが、スターク予想自体、類体の構成問題に使えそうだという期待はあったみたいですね。プレプリント内のTheorem 1.9が類体の構成に関する主張ですが、総実体 $F$ の最大アーベル拡大 $F^{\text{ab}}$ が、Brumer–Stark単数なるものを用いて構成されています。

いずれにしても、このような手法を用いて総実体上の類体が構成できたという主張なわけですね。

なお、プレプリントの中にも書いてあるのですが、今回の結果をもって「ヒルベルトの第12問題」を解決したと言って良いのか、という点については十分配慮して発言する必要がありそうです。

というのもヒルベルトの設定は「代数体 $K$ に対して特殊値を添加することで最大アーベル拡大が得られるような「関数」は存在するか」という問題だったわけです。ヒルベルトの設定は少しふわっとしているものの、関数が存在するかという点が一つのポイントだったわけです。

その意味では、プレプリントにおいて次のような記述があります：

It is unclear whether Hilbert would have accepted the combination of Theorems 1.6 and 1.9 as a solution to his 12th problem for totally real fields F. Firstly, our solution requires p-adic analysis for infinitely many primes p, rather than classical complex analysis. Secondly, our analytic formula requires p-adic integration rather than simply evaluating an analytic function at special points.

今回の手法は $p$ 進解析に基づく方法を必要としており、ヒルベルトが当初想定していたような複素解析的な方法ではないというわけですね。クロネッカーの青春の夢のような、解析関数の特殊値ではなく、p進積分と呼ばれるものを計算する必要があると。

その下の部分で、問題の解決になっている旨の根拠を述べている気もするのですが、私には理解できませんでしたので、これ以上の言及は避けます。

一定の意味において、総実体上のヒルベルトの第12問題を解決した、と解釈できるのかもしれません。

いずれにしても、数学の世界がどんどん進展していっているというのは喜ばしいことですね。

著者のDasguptaさんは、2017年に開催された岩澤理論の国際研究集会（Iwasawa2017）のスピーカーだったのですが、実は辻もその場に居合わせていました。なので、遠目にDasguptaさんを見たことがあります。笑

ちょうどそのタイミングで、Dasguptaさんの誕生日だったそうで、オーガナイザから誕生日ケーキが振舞われていました。このときに「誕生日に欲しいものは何か？」というようなことを聞かれて、「スターク予想の証明」とおっしゃっていた気がします。
（私が英語を聞き取れていれば。）

あれから３年半ほどたって、本当に成果を挙げたというわけですね。かっこいいなと思いました。
（もちろん、まだ査読が完了したわけではありませんが。）

リアルタイムでこういった進展が見られるというのは、現代を生きている我々の特権だと思います。クロネッカーやヒルベルトはこのような成果を知らないわけですからね。

数学ファンとしては、今後もこうした進展を楽しんでいきたいと思っています。

それでは今日はこの辺で！