折り紙で３次方程式が折れるわけ（前編）

《前回の記事はこちら》　正七角形の折り方：完成までの14のステップ - tsujimotterのノートブック

前々回の記事では、正七角形の折り方を１４ステップに分けて解説した訳ですが。
想像以上に反響があって tsujimotter は動揺しております。ありがたやーありがたやー。

このブログは、普段はめったに反応など聞けないのですが、今回は珍しくブックマークやtwitter等でコメントがついたのでした。

そのコメントで特に多かったのが、

「折り紙で任意の三次方程式が解ける」ってどういうこと？

というような疑問です。

１４ステップを１つ１つ検証していくと、三次方程式を解いている箇所は「手順４」であることがわかりました。手順４の図を再掲しておきます。（後の説明のために、前回とA, Bを交換して書いています。）

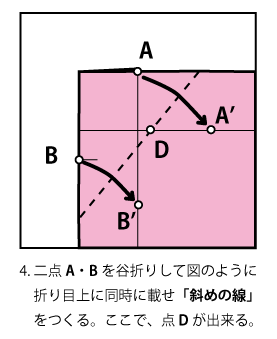
実際に折ってみるとわかりますが、なんとなく折りづらい部分ですよね。
でもここが大事なんです。

今回と次回の２回に渡って、手順４が「どういう仕組みで３次方程式を解いているのか」という点について数学的な裏付けをしたいと思います。
使っている数式や定義は高校数学を超えないものですので、よろしければ辛抱強くお付き合いくださいませ。

前編の本エントリは、３次方程式の準備段階として、点を線に折り合わせることの図形的な意味を考えてみましょう。

手順４を分解して、折り目線の正体を探る

まず、手順４を2つの手順に分析してみましょう。

手順4-1：点 を直線 上の点 におく。
手順4-2：点 を直線 上の点 におく。
これを「同時に」行う。

この「同時に」という点がポイントなのですが、ややこしい部分でもありますので、まずは「手順4-1」だけ抜き出して考察したいと思います。

手順4-1：点 を直線 上の点 におく。

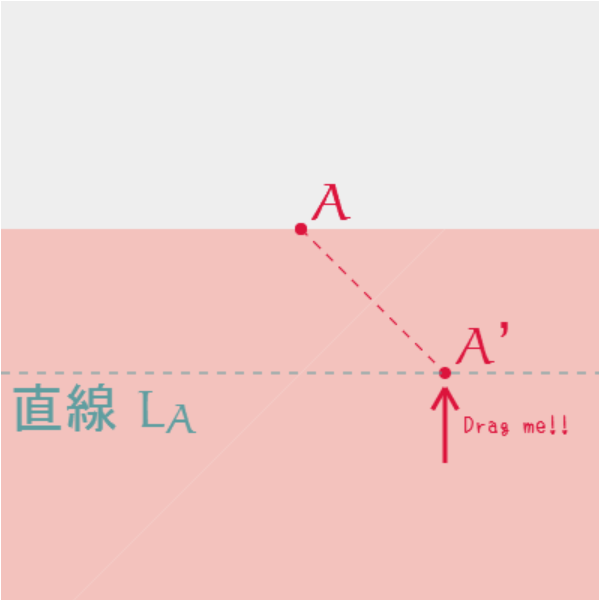
この操作によって作られる「折り目の線」は いったいどのような直線なのでしょう。

まずは自分でやってみよう

というわけで、自分で挑戦してみたい方のために、次のようなサイトを作ってみました。

折り紙が作る図形 - http://tsujimotter.info/origami/

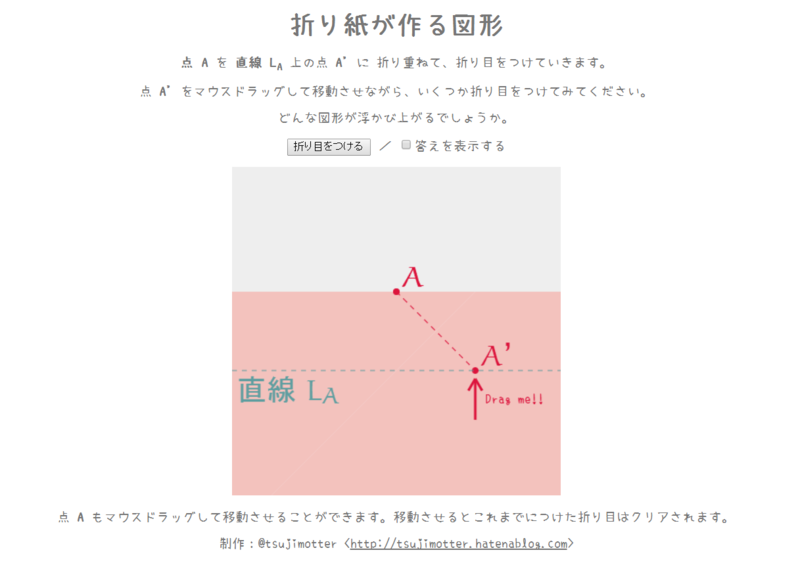
使い方は簡単です。

• A' をドラッグして移動させてみてください。好みの位置に合わせることが出来ます。
• 移動させたら「折り目をつける」ボタンを押してください。すると折紙が折り重なって A を A' に重ねたときにできる「折り目の線」を引くことが出来ます。
• 折り目の線は、繰り返しつけることができます。いくつか折り目の線を付けてみてから、それらの線がどのような線か予想してみましょう！

一通り遊んでみたら、以下の解説をどうぞ♪

解説はこちら

まず、１本「折り目の線」をつけてみましょう。

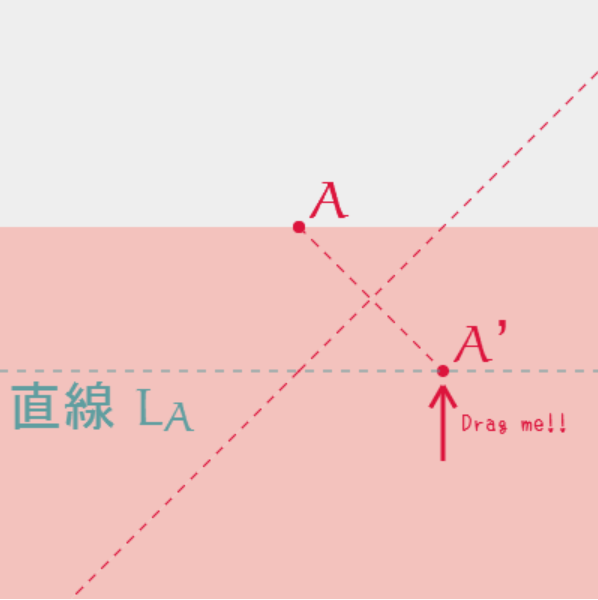
中点になっていますね。あとは、「２点を結ぶ直線」に垂直であることくらいでしょうか。

うーんよくわかりませんね。

Aをずらして何本か引いてみたらわかるでしょうか。

ほれ一本。

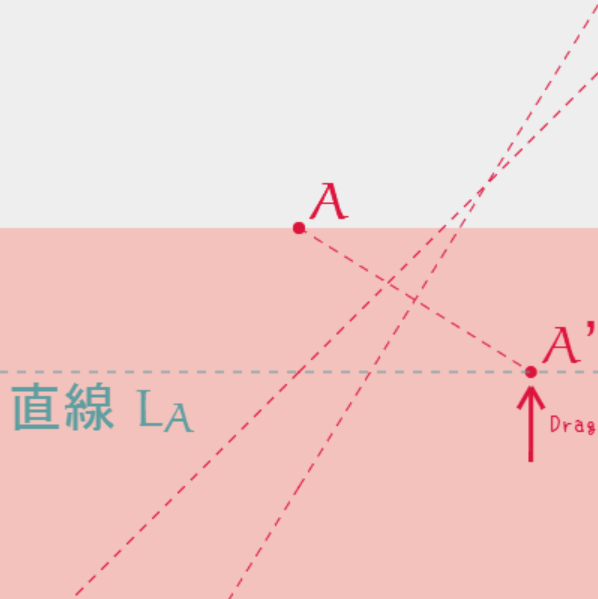
もう一本。

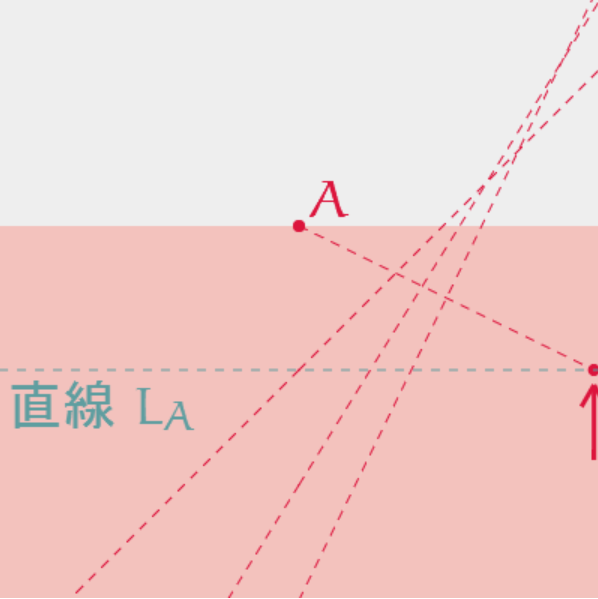
そういえば、ちょうど中心に線を引くとどうでしょう。

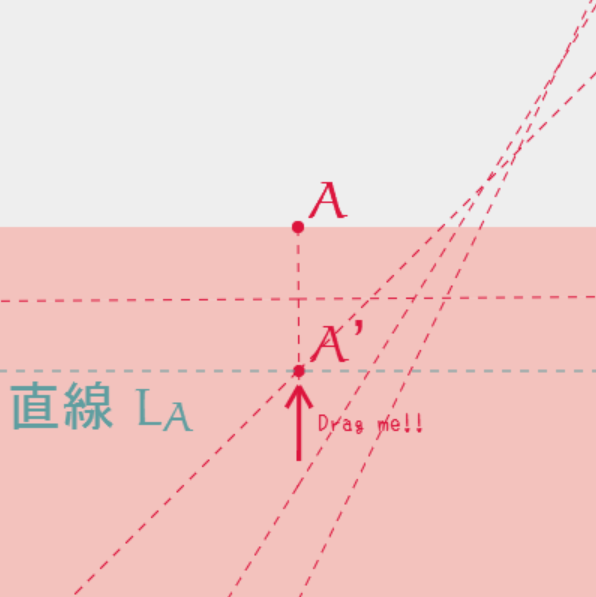
左側もいってみましょうか。

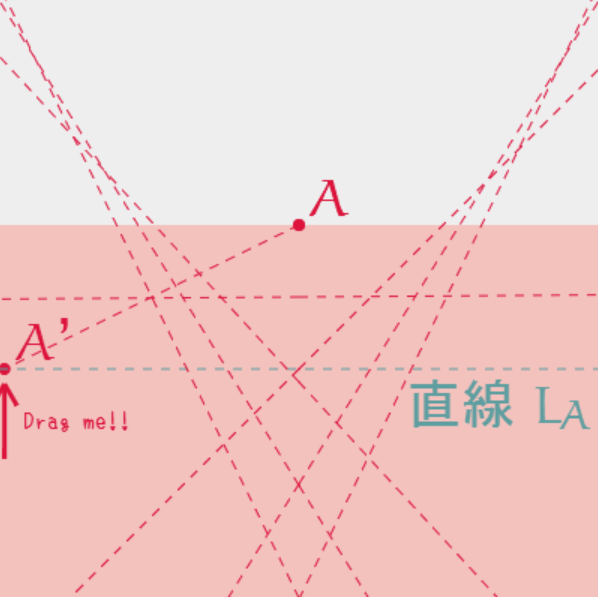
ケチらず大量に追加していきましょう。

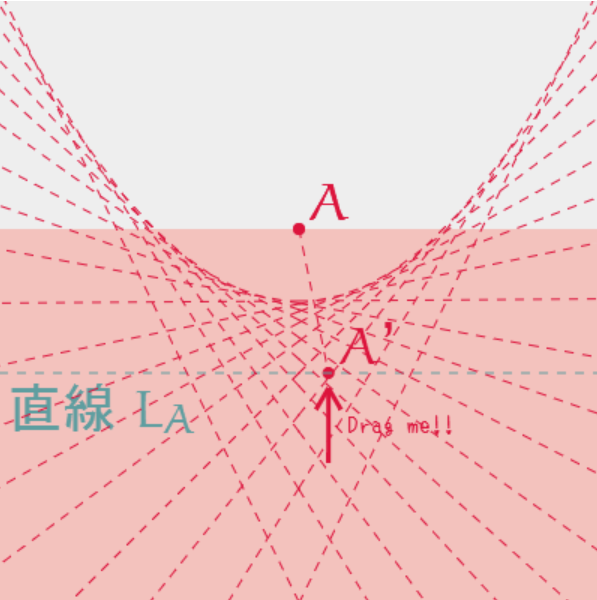
あれ、点をつないでいくと・・・。

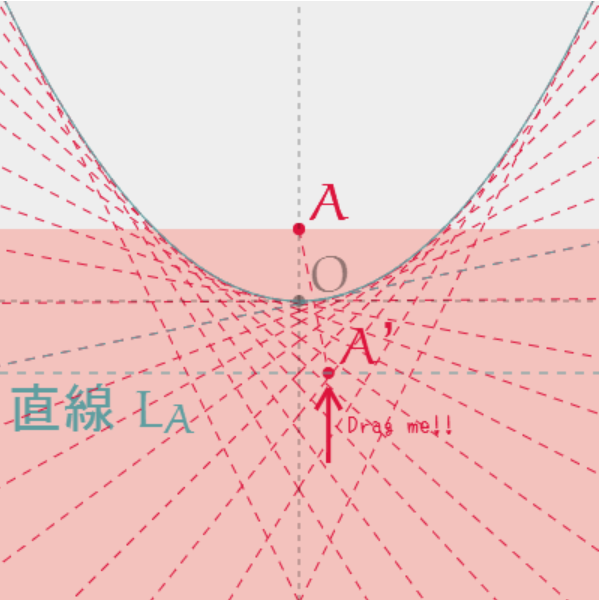
あーーーーーー！

って思った人、せいかい！

そう、これは 放物線 です！

すなわち、この操作によってできた「折り目の線」は「放物線の接線」だったのです。

もちろん、次の手順4-2によって作られる「折り目の線」も、同様に放物線の接線になります。

手順4-2（再掲）：点 を直線 上の点 におく。

したがって、これら２つの手順を合わせて手順４という操作によって、放物線が２つできるのですね。

手順４ではこれらを「同時に」行うわけですから、２つの放物線の「共通接線」を求めていることになります。

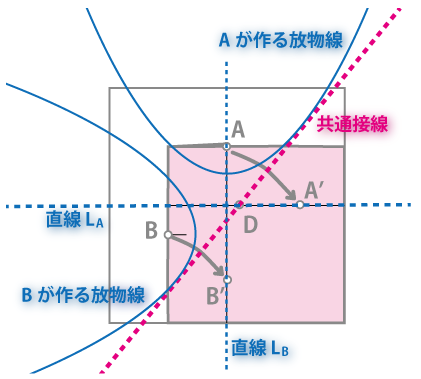
まとめとおまけ

以上の、結果をまとめておきましょう

• 手順4-1, 4-2 では、それぞれ１つずつの放物線の接線が得られる。
• 手順４では、これらを同時に行うから、２つの放物線の「共通接線」が得られる。

tsujimotter 的には、この「放物線の発見」は結構な感動ポイントだと思うのです。教科書とかだと淡々と結果だけ書いていたりして物足りないですよね。
楽しんでいただけましたでしょうか。

次回の後編では、ついに念願の三次方程式の謎に迫ります！

それでは、お楽しみに♪

《次回の記事》　折り紙で３次方程式が折れるわけ（後編） - tsujimotterのノートブック（追加しました！）

参考文献

折紙の数学―ユークリッドの作図法を超えて