約率、密率、連分数：円周率の近似値のお話

今日は 7月22日ということで、円周率のお話をしたいと思います。

円周率とは、「円周を直径で割った比」のことで、次のように定数であらわすことができますね。

《円周率》

$\pi=3.14159265358...$

この式の小数点以下2桁までとると 3.14 なので、3月14日は「円周率の日」と呼ばれています。

ところで、「7月22日と円周率に何の関係があるの？」と思うかもしれません。

実は 7月22日も円周率にまつわる記念日なのです。
正確に言うと「円周率近似値の日」です。

本エントリでは、「円周率近似値の日」に関連した「約率」と「密率」という２つの分数を紹介したいと思います。

約率

「円周率近似値の日」という呼び名は、紀元前３世紀にアルキメデスが発見した $\displaystyle \frac{22}{7}$ という円周率の近似分数に由来しています。
ちょうど、7月22日の日付をイギリス式の英語表記にすると、22/7 となるためです。

この数は 3.142857... と計算されるので、小数点以下2桁まで一致します。
円周率の粗い近似という意味も込めて $\displaystyle \frac{22}{7}$ は「約率」と呼ばれています。

《約率》

$\displaystyle \pi \fallingdotseq \frac{22}{7}$

ちょっと話が逸れますが、 $\displaystyle \frac{22}{7}$ のような分数で表された近似値をみると、少し違和感があるかもしれません。
現代に住む私たちは、円周率を表すときに小数を使うことが多いですからね。
アルキメデスの当時、ヨーロッパには小数という概念はなかったそうなのです。

ヨーロッパで最初に小数が用いられたのは、1585年のオランダのシモン・ステヴィンからで、かつては分数で表すことが主流だったわけです。

正確にいうと、アルキメデスの当時は仮分数という概念もなかったので、 $\displaystyle \frac{22}{7}$ という表現はされずに、 $3$ と $\displaystyle \frac{1}{7}$ のように帯分数で考えられていたようです。
$\displaystyle \frac{1}{7}$ のような整数の逆数は、単位分数と呼ばれていて、たとえば古代エジプトでは分数といえば単位分数しかなかったのです。

密率

アルキメデスが発見した約率のほかにも、円周率の近似分数として次のような分数が知られています。

５世紀の天文学者であり数学者である祖沖之（そちゅうし）は「密率」と呼ばれる分数を発見しました。

《密率》

$\displaystyle \pi \fallingdotseq \frac{355}{113}$

この数は、計算すると 3.14159292035... となりますが、小数点以下6桁まで一致するという恐ろしい近似精度をもっています。
約率と比較して、より精密な近似であることから「密率」という名前がついているのです。

実際やってみるとわかりますが、密率以上の近似精度を持った分数を作ることは、非常に困難です。
密率以上の近似精度の分数を作るためには、分母の大きさを 16604 以上にする必要があるのだそうで、これを超える近似式が登場したのは祖沖之から1000年以上たった後でした。

そんな近似精度の高い密率ですが、祖沖之はいかにしてこれを見つけたのでしょうか。
おそらく、適当に計算して見つけたというわけではないでしょうから、何かしらの考え方に乗っ取って発見したのでしょう。祖沖之がどのような方法で密率を導出したかは、歴史家の中で未だに議論が分かれるようです。

近似分数と連分数

約率、密率は円周率を近似する良い分数です。これらは適当に見つけられたものなのでしょうか。

これらの近似分数が、「単なるあてずっぽう」ではなく、円周率の「正当な近似値」であることの１つの説明として「連分数」を使う方法があります。

連分数とは、分数の中に分数が入れ子になって繰り返し現れる式のことです。連分数を使うと、円周率は次のように表すことができます。

《円周率の連分数展開》

この式は、ランベルトという数学者が彼の著書で1767年に示しました*1。
証明は難しいのでやりませんが*2、この右辺は単なる近似ではなく、左右の式は厳密に一致するのです。
また、円周率は無理数であることが知られていますので、この連分数は無限に続いていきます。

この連分数を途中で区切ることで、円周率の任意の近似分数を作ることができます。
面白いことに、この連分数を使うことで、約率や密率が円周率の近似分数として自然に導かれるのです。
やってみましょう。

まずは、第一次の近似。

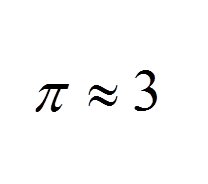
f:id:tsujimotter:20140722142026p:plain:w68

当然ですが、3に近似されるという当たり前の結果です。

続いて、第二次の近似。

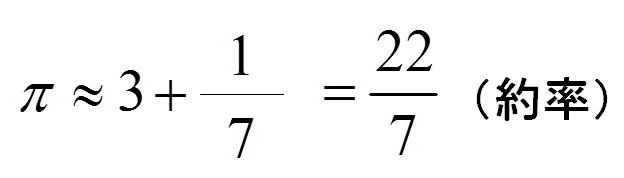
f:id:tsujimotter:20140722142049p:plain:w180

約率が現れました。

第三、第四の近似です。

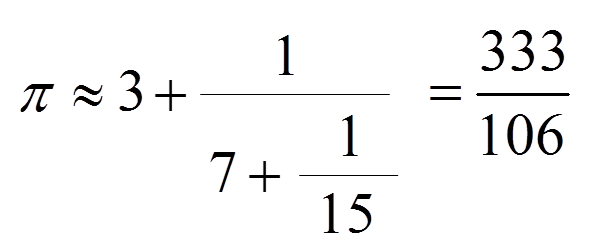
f:id:tsujimotter:20140722142111p:plain:w180

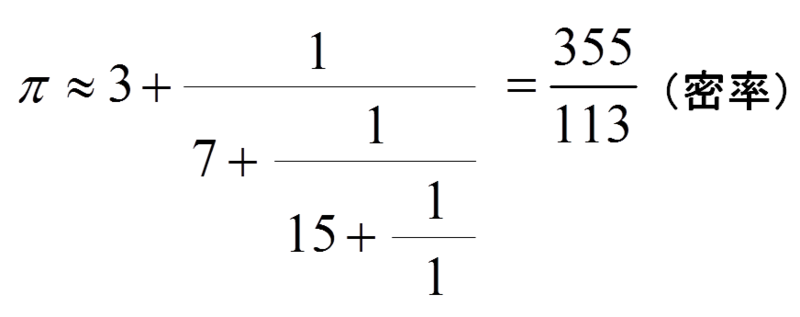
f:id:tsujimotter:20140722142116p:plain:w240

あっさりと密率が登場しましたね。
これで約率、密率がそれぞれ円周率の近似分数であることが示せました。

また、約率が密率の近似分数になっていることも、今回の結果からわかりますね。

まとめ

今回は、円周率近似値の日にかこつけて「約率」「密率」という２つの興味深い近似分数について紹介しました。

また、これらの式は単なるあてずっぽうではなく、円周率の連分数への展開を通して、きちんと意味のある近似分数であることも説明できました。

もちろん、この説明は現代に住む私たちの再解釈なので、アルキメデスや祖沖之がこの方法で見つけたとは到底思えません。
しかしながら、連分数という１つメタな視点を通してみることで、単なる数に見えていた２つの分数も、実はそれぞれに関連していて密率が約率を包含しているという構造が見えてくる、という点が私は興味深いなと思っています。

最後に参考文献として、祖沖之が密率を導出した方法に関する１つの考察のURLを紹介します。多少式が込み入っていて難しいですが、興味深い方法なので読んでみると面白いかと思います。

それでは、短いですが今日はこの辺で。