こんにちは! 日曜数学者のtsujimotterです!
早いもので、日曜数学者と名乗り始めてから5年半が経ちました。その間、色々な数学を勉強して、成長もしてきたと思います。昔憧れた、名前しかしらなかった高度な理論も、だんだんと理解できるようになってきました。このことは、最近特に実感しています。
今回のテーマである 虚数乗法論 も、初期の頃から興味を憧れを抱いてきました。
tsujimotter.hatenablog.com
あれから勉強が進んできて、理論についてまとめようと試みた記事もありました:
tsujimotter.hatenablog.com
しかしながら、上の虚数乗法論シリーズは未完のままです。当分続きは書けそうにありません。
大きな理論をまとめるのは大変だというのが理由の一つです。もう一つの理由は、そもそも楕円曲線の一般的な定義など、下準備をするのが大変だったというところにあります。
そこで考えたのですが、理論を体系的にまとめるのではなく、何か具体例を決めて、それを紹介するというのもよいのではと思いました。
題して 「具体例を通して学ぶ虚数乗法論」 です。

また、虚数乗法論は ガロア理論・類体論・楕円曲線論 を前提とした高度な理論なので、一般論を展開していくと難しくなりがちです。
難しい話は読者を選ぶのも事実です。けれども、やっぱり理論の内容は面白いので、もっと多くの人に知ってもらいたい。その面白さ・美しさを伝えられるようになりたい。その意味でも、具体例があった方が読んでもらいやすいはずだと思いました。
今回の記事は、以下のような構成で進めたいと思います。コンピュータの手を借りて 具体例 を計算しつつ、虚数乗法論のある意味「花形」の一つである クロネッカーの青春の夢 に向かう話を展開したいと思います。
目次:
《前編》
《後編》
- 円とのアナロジー
- 類体論の復習とヒルベルト類体
- クロネッカーの青春の夢
- おわりに
後編のリンクはこちら:
具体例を通して学ぶ虚数乗法論(後編) - tsujimotterのノートブック
前編・後編に分かれていますが、後編の方も すぐに公開する予定です 既に公開されています。よろしければぜひご覧になってください。
部分的な内容に対してでも構いませんので、興味を持ったところ、面白かったところなど感想いただけると嬉しいです。
Sagemathについて
本記事では、具体例を計算するのにコンピュータの力を借りたいと思います。Sagemath というシステムが便利なので、これを使います。
www.sagemath.org
上のページに行くと「Cocalc」というサイトがあり、そこではオンライン上でSageの機能を使うことができます。インストール不要なので便利です。アカウントを作る必要がありますが、たとえばTwitterやGithubのアカウントを使って、比較的簡単に登録できます。登録したら、Sagamathワークシートを作成して、その上でコードを打ち込んで実行してみてください。
Sagemathのコードも随時載せていきます。もちろん、ただ読んでいただくだけでもよいですが、一緒に計算してみると楽しいかと思います。
なお、実際にやっていく上でわからないことも出てくるかと思います。そんなときは、私はSagemathのオンラインリファレンスで確認しています。毎回、Google で "sagemath elliptic curve" のように計算して、なんとなくで使っています。基本的に日本語での解説はあまりないので、日本語で見つからなかったら英語で再検索するのが良いかと思います。
以下に有用なリンクを紹介しておきます:
木村先生によるSageの解説。基本的な使い方から、数論で使える話まで丁寧に載っています:
木村巌「数論研究者のためのSage (Algebraic Number Theory and Related Topics 2010)」
https://repository.kulib.kyoto-u.ac.jp/dspace/bitstream/2433/196245/1/B32_009.pdf
横山先生の楕円曲線に関する解説で、このPDFにはいつもお世話になっています。「計算する立場からの〜」というのは、今回のテーマにぴったりですね:
横山 俊一「計算する立場からの楕円曲線論入門」
http://www.comp.tmu.ac.jp/s-yokoyama/lectures/2015-2018/files/2014Yamagata.pdf
本日の主役
今回は、こちらの楕円曲線
に主役を演じてもらいます。右辺が についての3次の多項式、左辺が
についての2次の多項式となっています。楕円曲線の定義はここでは述べませんが、だいたいこんな感じの形をした曲線を 楕円曲線 と呼びます。
この具体的な楕円曲線を通して、虚数乗法論におけるさまざまな概念を紹介していけたらと思います。
愛着を持ってもらうために、楕円曲線 のグラフを書いてみようと思います。このような形をしています。
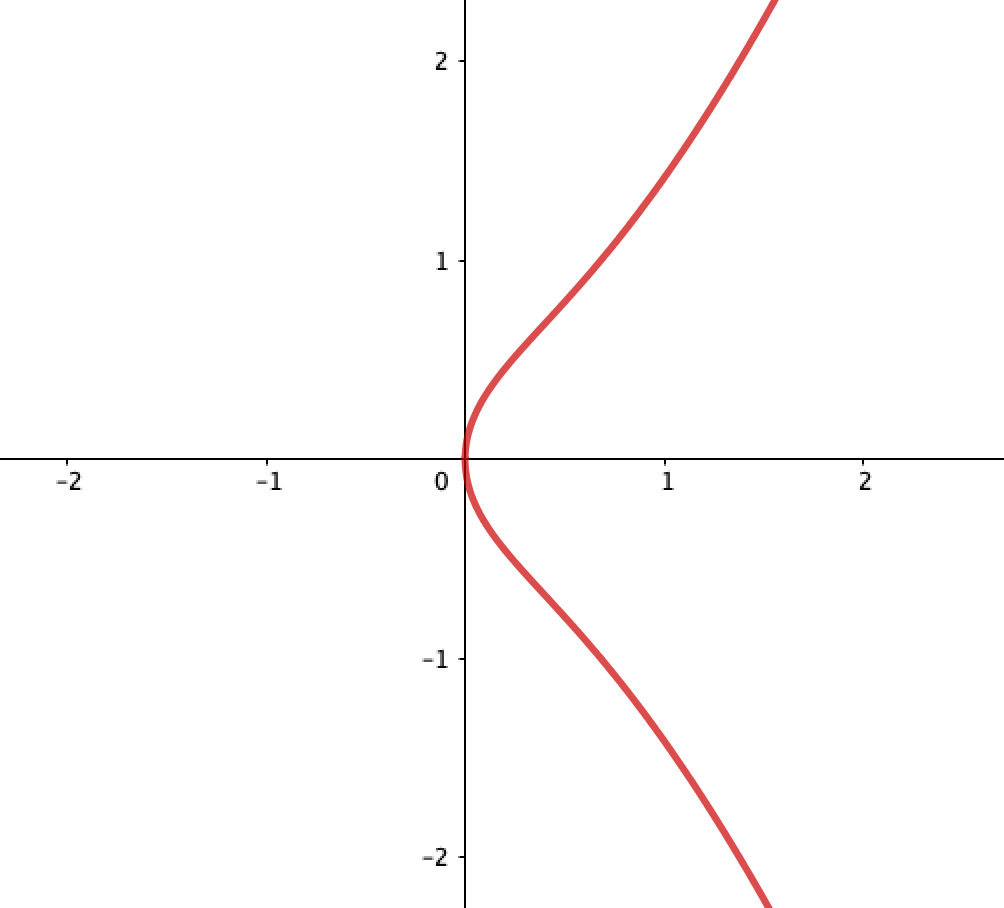
Sagemathを使って、上記の楕円曲線を定義する方法について説明しましょう。
E = EllipticCurve([0,0,0,1,0]); E
のコマンドを実行すると
Elliptic Curve defined by y^2 = x^3 + x over Rational Field
という結果が返ってくるかと思います。これで、楕円曲線 を定義できたことになります。
という形で定義される 上の楕円曲線を、次のコマンドによって得ることができます。
E = EllipticCurve([a1,a2,a3,a4,a6]); E
上の例では、 でそれ以外の係数は 0 としたということですね。
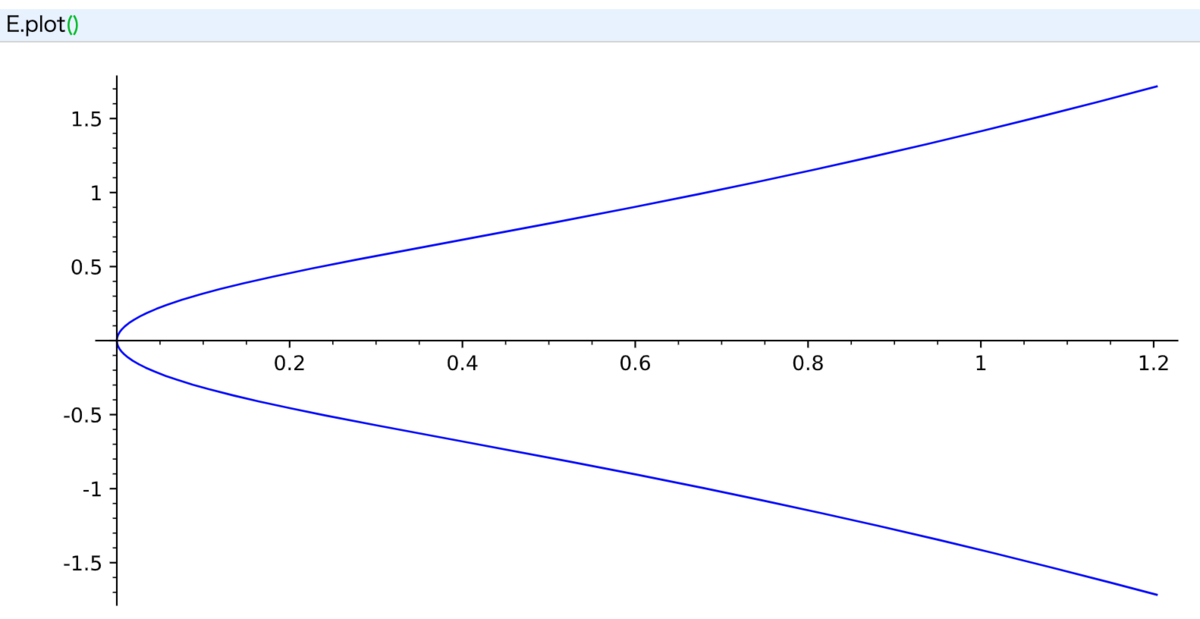
上のコマンドに続けて以下のコマンドを打つと、
E.plot()
結果はこのようになるはずです:
便利そうですね!
楕円曲線の加法
まず、楕円曲線の有理点には 加法 が定義できるという話をしたいと思います。
前節の楕円曲線の説明では、 という方程式そのものが楕円曲線であると説明しました。一方で、普段、我々がたとえば円のような曲線を考えるときに、以下の2種類の捉え方をすると思います:
という方程式そのものを円と呼ぶ
という方程式を満たす点の集まりを円と呼ぶ
代数幾何の言葉においては、後者を区別して「有理点」と呼ぶことが多いです。
ただ、有理点を考えるときには、その座標の数の集合(基本的に数の集合としては「体」を考えます)を明確に意識する必要があります。
楕円曲線 の
上に座標をとる点集合を
の
有理点 と呼び、
と表すことにします。すなわち
という集合を考えることになります。
本記事においては、楕円曲線の点の座標を一貫して複素数体 でとることにします。なんで複素数と思うかもしれませんが、複素数体
は代数閉体なので、このような体を考えることが都合よい場合もあるのです。
の定義に
という点が加わっていますが、これは 無限遠点 と呼ばれる点です。
前節の楕円曲線の図では、右上と右下に向かって曲線が続いているように見えると思いますが、この無限大のかなたにある点が無限遠点です。実は、無限遠点において、右上に向かう線と右下に向かう線が「つながっている」と思うことができます。つまり、前節の図は「ループ状の図形」を表していたということですね。
この説明はあくまで雰囲気を伝えるだけのものなので、数学的には正確ではありません *1。とにかく無限遠点を加えることで、いろいろと理論がうまくいくのです。
さて、無限遠点を加えた楕円曲線 の
有理点
を定義したわけですが、
は単なる集合ではなく、加法という演算が入ることについて説明しましょう。加法の構造は楕円曲線の持つ著しい性質であり、これによって理論的に面白い対象になります。
楕円曲線の任意の2点 を考えます。これらの点を用いて
という
の点を作ることができます。
点 の座標
を具体的に表す方法について述べましょう。ここでは、少しだけ一般に
という方程式で表される楕円曲線 について計算したいと思います。あとで
とすれば、私たちの
における加法の式が得られます。
の座標をそれぞれ
とすると、その関係は次のようになります:
初めて見た方は、いったいどうしてこのような式が現れるのかと驚くのではないかと思います。
色々な説明が考えられますが、ここでは幾何的な説明を試みようと思います。
を考えるといったばかりですみませんが、図示が難しいので
を考えます。これであれば、
軸と
軸で2次元平面にプロットできます。
上の任意の相異なる2点
をとって、その2点を通る直線を引きます。
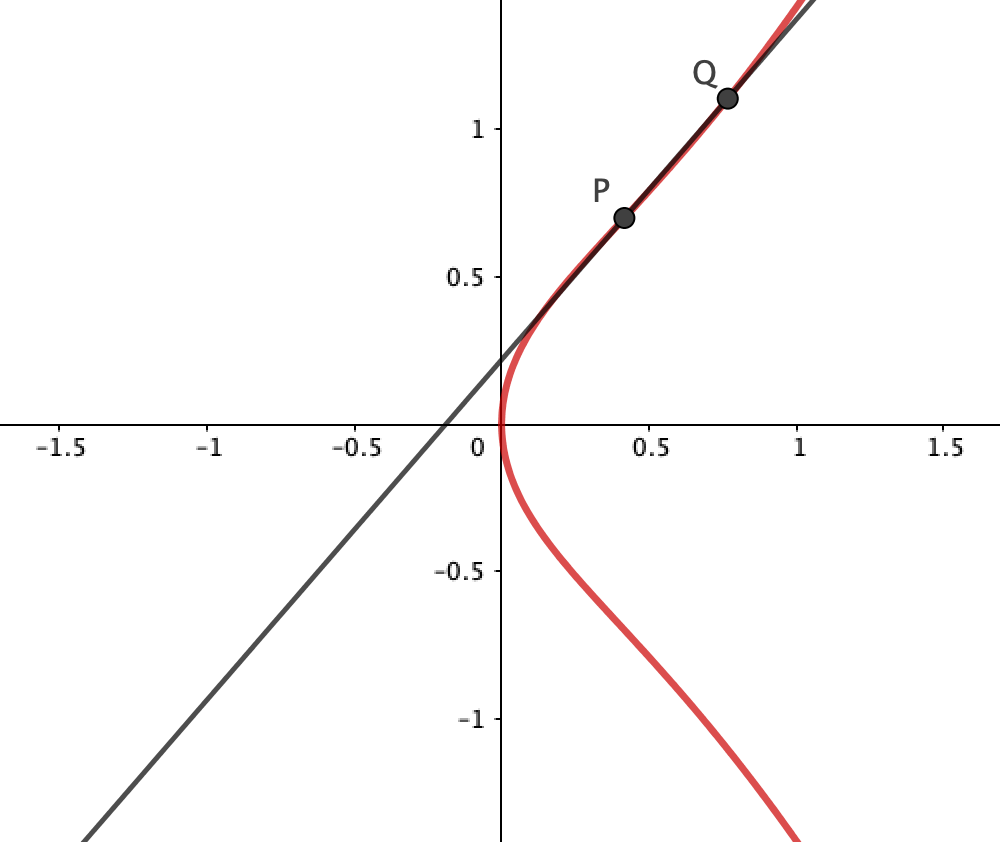
この直線は、必ず 上の
とは異なる1点と交わります。直線が楕円曲線と相異なる3点で交わるという事実は、ベズーの定理 と呼ばれます。
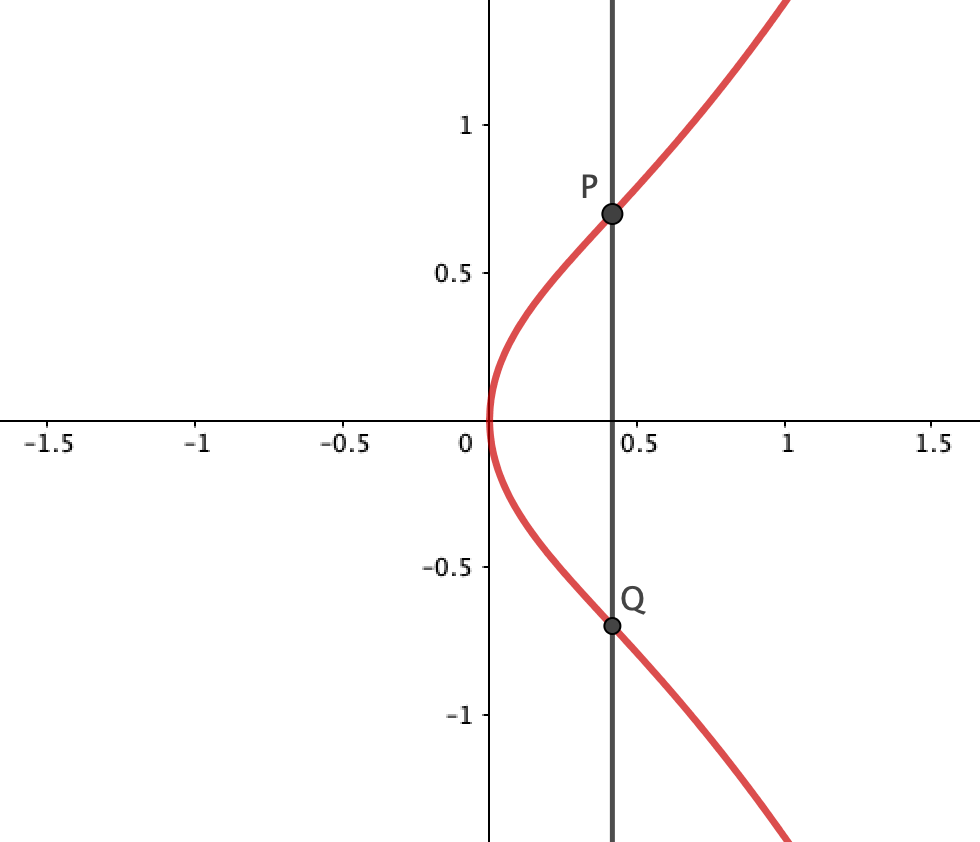
この場合、 の結果は無限遠点となります。
このようにして得られた新しい点を とし、
を
軸で線対称に写した点を
とするのです。
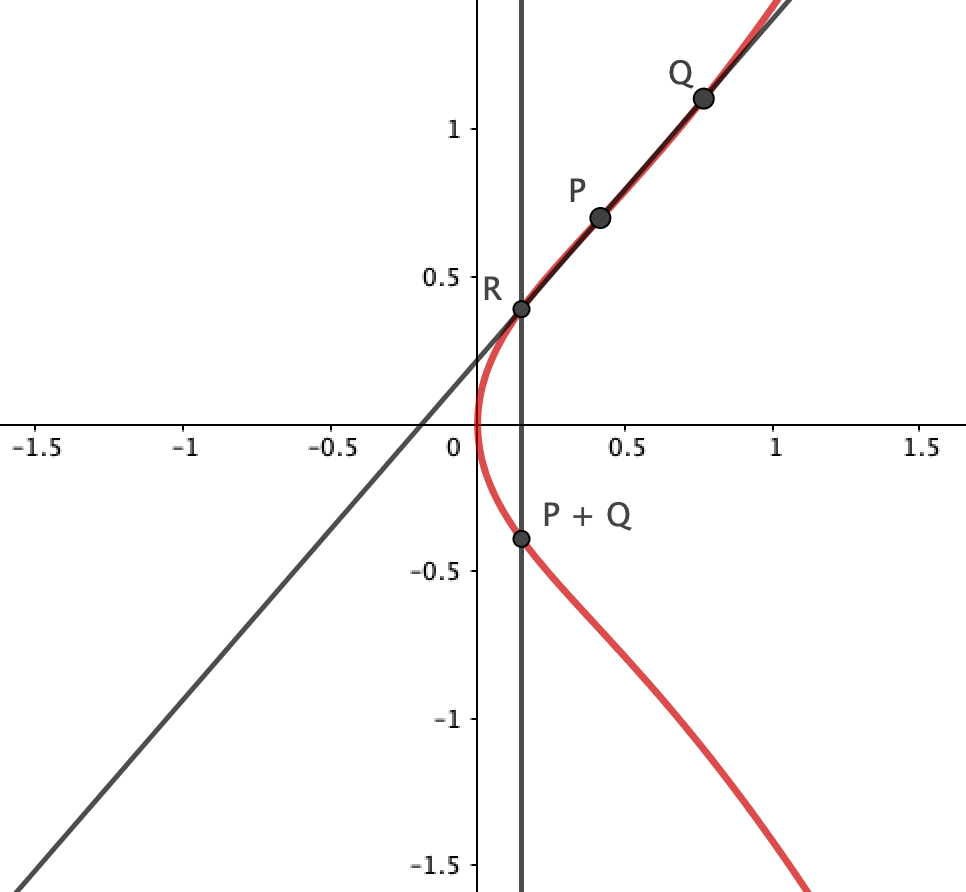
点 の座標を具体的に計算すると上のようになります。
上の議論では、 を仮定していましたが、
のときの
はどのように定義すればよいでしょう。
この場合は、点 における「接線」を考えてください。
における接線が
と交わる点を
軸対称に折り返した点を
とします。この
の座標
を、
を用いて具体的に計算すると、次のようになります:
かなり複雑ですね。2つ目の については こちらのページ から拝借したため、自分で計算していませんのでご注意ください。
以上は における加法の計算式ですが、上の式自体は形式的に
の点座標にも適用できます。これが
の加法の定義式となります。
ここまでの議論により楕円曲線 の加法
が定義できました。
加法というからには、単位元 が存在して、任意の点
に対して、以下の4法則が成り立ってほしいかと思います:
- (結合則)
- (単位元)
- (逆元)
- (交換則)
このような法則を満たす集合を アーベル群 といいます。結論としては、 は単位元を無限遠点
として、加法についてアーベル群の構造を持ちます。
m倍写像とm等分点
続いて、 倍点 と
等分点 を定義したいと思います。
任意の点 を
の「1倍点」とあえて呼ぶことにします。また、先ほど定義した
は2倍点です。3倍点
を
として定義します。同様に を定義していきます。これで、自然数
に対して
が定義できたことになります。
今度は について
を定義しましょう。
まず、 における
は無限遠点
とします。次に
を
とします。同様に
を
、
を
のように定義していきましょう。
以上によって、任意の整数 に対して、
倍点
を定義できたことになります。
また、 に対して
を対応させる写像
を 倍写像 と呼ぶことにします。
倍写像は、アーベル群
からアーベル群
への準同型写像になっています。すなわち
が成り立つということですね。
特に、自分から自分への準同型写像なので、このような写像を 自己準同型写像 といいます。
さて、準同型写像があったら、その「核」を考えたくなると思います。準同型写像の核とは、準同型写像の像が単位元であるような、定義域の部分群のことです。
倍写像の核
は
と表される集合です。要するに「 倍して
(無限遠点)になる集合」のことですね。これを
の
等分点 と呼び、
と表すことにします。
改めて は
の部分群になっていることに注意しましょう。この
がとても重要な役割を果たします。
このあたりで、少し具体的な計算をしてみましょう。
E[2] の計算
の2等分点
を計算します。これは定義から
となるような点 を考えればよいでしょう。
ただ、 をそのまま計算するのは大変です。そんなことをしなくても、
が無限遠点ということなので、幾何的に考えれば
とすれば十分であると気づきます。
すなわち、 で
とした
の解が、 の
座標となります。解は
のいずれかとなります。 なので、
の点は
となります。無限遠点 は
なので、
の元であることを忘れずに。
上に出てきた多項式 を楕円曲線
の 等分多項式(division polynomial) というそうです。実際、sagamathを使って等分多項式を次のように計算することができます:
E = EllipticCurve([0,0,0,1,0]); E f = E.division_polynomial(2); f
結果は次の通りです:
Elliptic Curve defined by y^2 = x^3 + x over Rational Field 4*x^3 + 4*x
が等分多項式ということですが、先ほどの多項式を単に4倍したものになっていますね。ちゃんと検算できました。
群構造も考えてみましょう。
と置くことにします。ここで楕円曲線の加法を計算すると
が成り立つはずです。また、加法を具体的に計算してみると
も成り立ちます。
つまり、 の点は、
を用いて
と表せるということがわかりました。
すなわち、任意の は、
を用いて
と表せるということです。ここからアーベル群の同型
が分かります。
Sagemathを使って実際に上の事実( が成り立つこと)について確認してみましょう。
の座標は
ではなく
に入っていますので、そのままでは計算できません。Sagemathでこのような点の加法を計算するためには、係数体を拡大する必要があります。
K.<a>=NumberField(x^2 + 1) E = EllipticCurve(K, [0,0,0,1,0]); E
1行目では係数体 を定義して、2行目でその係数を "EllipticCurve" の第1引数にセットしています。
"NumberField" は代数体の意味で、その定義多項式が だということです。さらに多項式
の根を "a" という定数に代入しています。この場合は
であり、後から "a" を定数として使うことができます。
さて、このような準備のもとで以下を計算します。
P = E(-a, 0); P Q = E(0, 0); Q R = E(a, 0); R 2*P 2*Q 2*R
結果は次の通りです:
(-a : 0 : 1) (0 : 0 : 1) (a : 0 : 1) (0 : 1 : 0) (0 : 1 : 0) (0 : 1 : 0)
は射影平面における無限遠点です。たしかに、
となっていることがわかります。
を計算してみましょう。
P + Q
結果は次の通りです:
(a : 0 : 1)
これは の座標
に一致しますね。たしかに
が成り立っています。
E[3] の計算
同様に の3等分点
を計算してみたいと思います。
任意の についての3倍公式を使って
となるような座標 を計算すればよいでしょう。ただ、3倍公式をそのまま計算するのはとても大変です。
次のような賢い式変形があります。
は
座標にマイナスをとるだけなので、
と
の
座標は等式で結ばれます。これにより等分多項式が得られます。
とはいえ、等分多項式を計算するのは面倒なので、やはりSagemathの力を借りましょう。
E = EllipticCurve([0,0,0,1,0]); E f = E.division_polynomial(3); f
結果は次の通りです:
Elliptic Curve defined by y^2 = x^3 + x over Rational Field 3*x^4 + 6*x^2 - 1
等分多項式が であることがわかりました。この解もやはりSagemathで計算できます:
solve(3*x^4 + 6*x^2 - 1, x)
結果はこちら:
[x == -sqrt(2/3*sqrt(3) - 1), x == sqrt(2/3*sqrt(3) - 1), x == -sqrt(-2/3*sqrt(3) - 1), x == sqrt(-2/3*sqrt(3) - 1)]
すなわち
ということです。
座標が4つあるので、それぞれに2つずつ
座標を考えると、全部で8点。これに無限遠点
を加えて、全部で9点が
の元になります。
ここから群構造を考えたいのですが・・・。ちょっと係数体が複雑すぎます。私には、楕円曲線の係数体を適切に計算できなかったので、Sagemathを使って加法を計算することができませんでした。というわけであきらめましょう。
まとめると、 は
点、
は
点あることが分かりました。
一般に、 は
点あり、群構造としては
となることが示せます。
長かったですが、楕円曲線の一般論についての話はここでおしまいです。
虚数乗法とは
お待たせしました。ここからは 虚数乗法 の話をしたいと思います。
前節では に対して
という自己準同型写像を考えました。アーベル群
の自己準同型写像とは
であって、 に対して
が成り立つものを言います。
ここで の 虚数乗法 とは、
の自己準同型写像
であって、
(
)と表されないもののことをいいます。また、
に対して虚数乗法
が存在するとき、
は虚数乗法を持つ といいます。
「なんだそんなことか」と思うかもしれませんが、これがまさしく虚数乗法の定義です。
私たちの楕円曲線 は、まさに 虚数乗法を持つ楕円曲線の一例 になっています。
具体的には、次の自己準同型写像が虚数乗法となっています。
まず、この行き先が に入ることは
を具体的に
に代入することで確認できます。実際、次のようになります:
ここで、 は
を満たすので、(左辺)=(右辺)が成立することがわかります。これで、写像の行き先が
に入ることが確認できました。
が準同型写像であることは、実際に加法公式に代入してみることで確認できます。とてつもなく面倒なのでここでその計算はやめておきますが、興味がある方はぜひやってみてください。
とにかく、今回はこれが の虚数乗法であることを信じて進めましょう。
さて、 が虚数乗法が持つとき、自己準同型写像全体を考えると面白い構造が見えてきます。
の自己準同型写像全体の集合を
と表すことにします。
とし、写像の間の加法
を、任意の
に対して
とすることで定義します。
ここで注意したいのは、上の式は という写像を定義する式になっているという点です。すなわち、
の点
における値を計算しようと思ったら、
を計算すればよいということですね。ここでの加法記号
は、楕円曲線
の有理点における加法を指しています。
さらに、 に対する乗法
を同様に定義したいと思います。しかしながら、加法とは異なり楕円曲線の点には乗法は定義されないため、全く同じようにはいきません。
は自己準同型なので、
の
による行き先が
に入っていることに注目します。行き先の点
に対して、再度
を適用すれば、合成写像
が定義できます。
よって乗法は、写像の合成 によって定義したいと思います。すなわち、任意の点
に対して
とすることで、 の積
が定義されます。
以上により、 に加法と乗法をそれぞれ定義することができました。これらの演算により、
は環構造を持ちます。
を 自己準同型環 といいます。
なお、加法の単位元は0写像(行き先がすべて になる写像)であり、乗法の単位元は恒等写像となります。
さて、虚数乗法を持たない楕円曲線においては、自己準同型写像は に対して
という形のものしかありませんから、
です。
一方で、我々の楕円曲線 はどうでしょうか。実は
となります。なんと、自己準同型環が ガウス整数環 になるのですね。
すでにお気づきの方もいるかもしれませんが、先ほどの虚数乗法
は、上の環同型によって に対応するものになっています。実際、
を2回合成すると
となり、 に一致します。たしかに、
を彷彿とさせる性質です。
一般に、虚数乗法を持つ楕円曲線 の自己準同型環
は、虚2次体のある整環(極大整環つまり「整数環」とは限らない)に同型となる ことが示せます。
これは極めて面白いことで、虚2次体 の整数環
に同型なもの(今回のケース)や、虚2次体
の整数環
に同型なものがあるということです。
より一般に、虚2次体の の整数環は
となることが知られていますが、それぞれに対応するような虚数乗法を持つ楕円曲線が作れるというわけです。
つまり、何が言いたいかというと、虚数乗法を持つ楕円曲線は虚2次体と相性が良い ということです。
楕円曲線は元々「幾何的」な概念として定義されましたが、楕円曲線に群構造が入ったことで「代数」との結びつきが出てきました。虚数乗法を持つ楕円曲線を考えることで、今度は「数論」との結びつきが出てきました。
ここからどんどんと数論色の濃い話が出てきます。今回の目的である クロネッカーの青春の夢 は、虚2次体上の類体が楕円曲線の 等分点を用いて表せるという驚くべき性質についての主張です。
だんだん面白くなってきました。
後編はこちら!
参考文献

- 作者:J. H. シルヴァーマン,J. テイト
- 発売日: 2012/08/25
- メディア: 単行本

The Arithmetic of Elliptic Curves (Graduate Texts in Mathematics (106))
- 作者:Silverman, Joseph H.
- 発売日: 2009/05/29
- メディア: ハードカバー

- 作者:J.H. シルヴァーマン
- メディア: 単行本
*1:厳密には「射影平面」という概念を導入する必要があります。