高校数学で習う「空間内の2直線間の距離」について考えてみたいと思います。
3次元空間内に2直線 があるとします。
が「ねじれの位置にある」とは、
が交点を持たず、かつ、平行でもないことを言います。このとき、2直線
の距離を考えてみたいと思います。
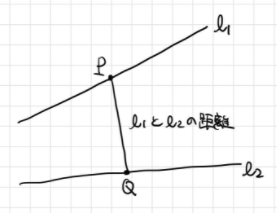
そもそも2直線の距離とは、というところから考えたいと思います。 の点
および
の点
を任意にとったとき、距離
の最小値を2直線
の距離と定義します。
ここで疑問に思うのは、そもそもこの最小値は存在するのか?、という問題です。2直線の位置関係によっては、2直線のそれぞれの点の距離がいつまでも漸近的に小さくなり続けるなんてこともあるかもしれません。この場合、最小値は存在しないことになります。もちろん、直感的にはそんな状況はなさそうに思えますが、証明される必要があると思います。
最小値が存在しなければ、2直線の距離は定義できない場合が存在するということになってしまいますね。
この記事の最後に述べるように、結果的には最小値は存在し、2直線の距離が定義できます。この事実って高校数学では証明されるのでしょうか? 少なくともtsujimotterはこの証明について聞いた記憶がありませんでした。証明が気になって眠れません。
というわけで、最小値が存在することについて自分なりに考えてみたのがこちらの記事となります。今回は「ベクトル解析」を使った証明ですが、もしかしたら、もっと簡単に考えることもできるかもしれません。
個人的に楽しかったのでまとめてみたという記事になりますので、おおらかな目でみてあげてください。別解などあればお気軽におしらせください。
(追記)
実は最後に書いたのですが、もっとシンプルな解決策があったようです。結果的には、前半で書いたような計算はしなくてもよかったのですが、計算していて楽しかったのでそのまま載せたいと思います。
2直線の距離を求めよう
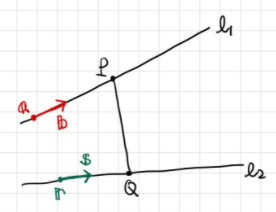
各直線上にある点をベクトルによって表現してみましょう。
直線 上のある1点の座標をベクトルを用いて
と表します。直線
の方向を指す方向ベクトルを
を考えると、直線
上の任意の点の座標は
と表せますね。
同様に、 上の点の座標ベクトルを
とし、
の方向ベクトルを
とすると、直線
上の任意の点の座標は
と表せます。
の点
と、
の点
の座標をそれぞれ
を用いて表したとき、2点
の間の距離の二乗
は、次のように表されます:
ここで、 を動かしたときの
の最小値が
の距離というわけですね。
ベクトルのノルムの二乗は、ベクトルの内積で表せます。これを使って を計算すると
最後に得られた式は、大変変数が多くてややこしいですが、 は定数であって、
は変数だと思うと、これは
についての「2次関数」ということになります。
具体的には
とおいて、係数を
のように設定すると、 となりますね。
そんなわけで、2変数2次関数の最小値問題ということになります。
今、 かつ
であることに注意しましょう。
(どちらも方向ベクトルのノルムなので。)
よって、 は1次式に落ちることはありません。
ここで、次節で示す2変数2次関数の一般論により、 のヘッセ行列
の行列式が正であれば、
はただ一つの最小値を持ちます。ヘッセ行列とは
で表される行列でした。
ヘッセ行列の行列式を計算すると
ということになります。
ここで
であれば、 ということになります。
のなす角を
としたとき、空間ベクトルの内積の性質より
であったことを思い出しましょう。上の条件は ということなので、これは
が平行でないことと同値です。
は、それぞれ
の方向ベクトルでしたから、これは
が平行でないという条件に他なりませんね。
したがって、 が平行でない場合は、
となり
はただ一つの最小値を持つことがわかりました。特に、定義より
が交点を持つ場合、
の最小値は
が交点を持たない場合(ねじれの位置)、
の最小値は正の値
となります。

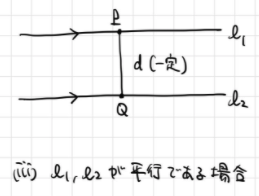
なお、 であれば、
が平行であるということです。この場合は、
が最小値をとるかどうか、式から直ちにはわかりません。
しかしながら、そもそもの問題に立ち返って、平行な を思い浮かべれば議論できます。
は平行なので、直線と直線の距離はどこでも一定になるわけです。
2変数2次関数の最小値
最後に
の最小値を求めることにしましょう。ただし、最小値を持つための仮定として、 および
を仮定したいと思います。
このとき、 はただ一つの最小解を持つことを示しましょう。
方針としては「平方完成」を2回用います。
まずは、 を
の2次式だと思って平方完成します。ここで
なので
で割れることに注意します。
さらに、残った の係数の分子
は、ヘッセ行列
の行列式そのものでした。今、
と仮定していますので、
で割ることは許されます。そのことを念頭に入れて、
についての2次式を平方完成しましょう。
というわけで、完成です!
新しい変数
および定数
とおけば
と表せます。
かつ
なので、この関数の最小値は
のとき
であることがわかりますね。
より
であることがわかります。また
より、
の値を
に代入することによって、 の値も一意に定まります。
よって、 のとき、
が最小となる組
が存在して、一意に定まることが示されました。
おわりに
そんなわけで、空間内のねじれの位置の場合に、2直線の距離が一意に定まることが示されましたね。そのときの点 の組も一意に定まるということでした。ひとまず安心して眠れそうです(?)。
2直線の距離の最小化問題が、2変数2次関数の最小化問題になるというのも面白いですね。たしかにこれなら最小値(=極小値)がただ一つに定まることも納得ができそうです。
それでは今日はこの辺で!
別解:共通接線を用いた証明
色々紹介しておいてアレなんですが、実はもう少し簡単に示す方法がありました。考え方としては、こちらのサイトの「裏技 共通接線」の方法がそのまま使えます。
math-juken.com
以下の流れで示すことができます:
- ① 2直線
の共通垂線
の存在が示せる。
- ②
が求める最小の距離である。
①については、上でやったように をそれぞれ座標ベクトル
で表示します。直線
と
が垂直より、
方向のベクトル
と
の方向ベクトル
の内積が
という条件が得られます。これを立式して
となります。同様に、 方向のベクトルと
の方向ベクトル
の内積が
という条件から
を立式します。すると、 についての連立1次方程式
が得られます。計算してみると が平行でないとき、連立方程式の解が一意的に存在することがわかります。ゆえに、この
により共通垂線と
との交点
が得られます。
②については、上のサイトで述べているような議論そのもので、直線 を上から見ると
を同一平面上に置くことができ、よって
の最小性が従う、というものです。
いやー、めちゃめちゃ簡単ですね・・・。平方完成していたのは一体何だったのでしょうか。
まぁ、でも色々な見方ができて面白かったですね!