続・XX + XY + 6YY の形で表せる素数 - tsujimotterのノートブック

これまで「類体論」の勉強をしてきましたが，その集大成となる記事を書きたいと思います。本日扱いたいのは，およそ一年前に紹介した以下の問題です。

$p = X^2 +XY + 6Y^2$ の形でかける素数はどのような法則を満たすか？

その一年前の記事はこちら：
tsujimotter.hatenablog.com

背景を簡単に説明しましょう。

まず， $X^2 + XY + 6Y^2$ の判別式 $D$ は

$D = b^2 - 4ac = 1^2 - 4\cdot 1 \cdot 6 = -23$

より得られます。判別式 $D = -23$ の二次形式には，全部で３通りの「類」が存在します。

$\begin{eqnarray} [X^2 + XY + 6Y^2], \; [2X^2+XY+3Y^2], \; [2X^2-XY+3Y^2]\end{eqnarray}$

上記の類のうち

$[X^2 + XY + 6Y^2]$

に属する二次形式のことを principal form と呼びます。

素数 $p$ が上記の二次形式の類のどれで表せるかは， $p$ によって異なります。

二次形式の言葉を使って，冒頭に述べた問題を書き直すと，

判別式 $D=-23$ の二次形式で表せる素数 $p$ において，特に $X^2 + XY + 6Y^2$ (principal form) によって表せるような $p$ の条件は何だろうか？

となります。この問題が本日のテーマです。

参考：「類」というのは， $SL(2, \mathbb{Z})$ の変換によって移れる "同値" な二次形式をクラス分けしたものです。詳細はこちらの記事を。
tsujimotter.hatenablog.com

同様の問題については，「 $N$ で割ったあまり」によって数多くの法則が見出されてきました。例えばこんな感じです：

$\begin{align} p \equiv 1 \pmod{4} \;\; &\Longleftrightarrow \;\; p = X^2 + Y^2 & (D = -4) \\ p \equiv 1 \pmod{3} \;\; &\Longleftrightarrow \;\; p = X^2 + XY + Y^2 & (D = -3) \\ p \equiv 1, 9 \pmod{20} \;\; &\Longleftrightarrow \;\; p = X^2 + 5Y^2 & (D = -20) \\ p \equiv 1, 7 \pmod{24} \;\; &\Longleftrightarrow \;\; p = X^2 + 6Y^2 & (D = -24) \\ p \equiv 1, 2, 4 \pmod{7} \;\; &\Longleftrightarrow \;\; p = X^2 + XY + 2Y^2 & (D = -7) \end{align}$

ところが，今回の問題においては，以上のような法則に当てはまらない「斜め上」の回答を見せます。

次のような保型形式を考えます。

$\displaystyle f(\tau) = \sum_{n=1}^{\infty} a_n q^n = q\prod_{n=1}^{\infty} (1-q^n)(1-q^{23n}) \tag{1}$

保型形式 $f$ の素数 $p$ 次における係数 $a_p$ を用いて， $p \neq 23$ に対しては以下のようにかけるというのです。

$\displaystyle a_p = 2 \;\; \Longleftrightarrow \;\; p = X^2 + XY + 6Y^2 \tag{2}$

そんな馬鹿な。

実際，このような法則が成り立つことを，以下の記事では数値的に確かめました。
tsujimotter.hatenablog.com

このような問題に対して，いったいどのように考えたらよいのでしょう。これまで通り類体論に基づいて理解することができるのでしょうか。

実のところ，今回の問題は単純な素イデアルの分解法則だけでは理解することができません。以下の３つの分解法則をそれぞれ考え，組み合わせることが必要になります。

二次体における素イデアルの分解法則（Q上の類体論）
ヒルベルト類体における素イデアルの分解法則
非可換拡大における素イデアルの分解法則

なかなか手強そうな問題ですね。

以下の記事では３部構成として，上記の分解法則を順に説明して，問題の本質に迫りたいと思います。

参考情報と補足

本日の記事に書いてあることは，伊藤哲史先生による

伊藤哲史「平方数の和で表される素数について」城咲新人セミナー
~~https://www.math.kyoto-u.ac.jp/insei/proceeding/2010/ito.pdf~~
https://drive.google.com/file/d/1RrC0WG676Hv3k2W0pfK6LY00hiC0kaR0/view
（リンク先が変わりました）

という文献に簡潔にまとまっています。

「 $p = X^2 + XY + 6Y^2$ でかける素数の法則」については，まさにこの文献で出会い，この文献に頼って理解を進めてきました。

とはいえ，この文献を読んでいたらあっさりわかったというものでもなく「諦めては挑戦し」をくりかえしてきました。上記の文献は，非常にわかりやすく教育的に書かれていて素晴らしいのですが，一方で基礎知識が足りないと理解できない箇所がいくつかあります。私自身は，類体論関連のいろんな本を読み漁って，なんとかここまで到達したという状況です。

今回の記事は「行間をできるだけ飛ばさない」を目標に書いています。勉強の過程でつまづいた経験をもとに，必要以上に途中計算を挟んだり，全体像がわかるような図を挟みつつ説明していきます。新たに勉強する人の参考になれば幸いです。

また，今回の記事はこれまでのブログで紹介した知識を仮定しています。

具体的には，以下のカテゴリに含まれる記事の知識は前提としたいと思います。まさに「これまでの集大成」という内容となっています。

tsujimotter.hatenablog.com

それでは，第１部からお話していきましょう。

１．二次体における素イデアルの分解法則

二次形式の法則の問題においては，「二次体」における「素イデアル分解法則」を考えるのが定石です。二次体の分解法則については，以下の記事で説明しましたので，これを利用していきましょう。

tsujimotter.hatenablog.com

二次体 $K = \mathbb{Q}(\sqrt{-23})$ とその整数環 $\mathcal{O}_K = \mathbb{Z}\left[\frac{1+\sqrt{-23}}{2}\right]$ を考えます。 $K$ における $p$ の分解法則を考えましょう。

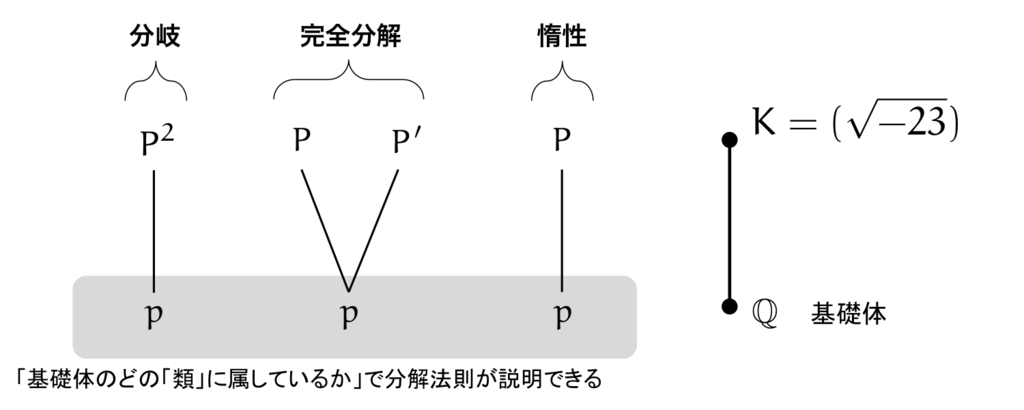
f:id:tsujimotter:20170122105920p:plain:w600

まず $p = 23$ のとき， $p$ は $\mathcal{O}_K$ において分岐します。この場合は，単純に

$23 = 1^2 + 1\cdot(-2) + 6\cdot (-2)^2$

と書けることがわかります。

判別式 $D = -23$ を割り切る素数は $23$ だけなので，分岐する素数は以上です。したがって，以降は $p \neq 23$ で考えましょう。

不分岐な素数 $p$ における分解法則は，二次体の分解法則によって

$\displaystyle \left(\frac{-23}{p}\right) = 1 \;\; \Longleftrightarrow \;\; (p) = P P' \tag{3}$

のように平方剰余を使って表せます。ここで， $P, P'$ は共役な $\mathcal{O}_K$ の素イデアルです。

平方剰余の相互法則によって，

$\displaystyle \left(\frac{-23}{p}\right) = \left(\frac{p}{23}\right) \tag{4}$

が成り立つため， $\bmod{23}$ における素数の分類によって分解法則が得られます。

したがって， $\bmod{23}$ の平方剰余から

$\displaystyle p \equiv 1, 2, 3, 4, 6, 8, 9, 12, 13, 16, 18 \pmod{23} \;\; \Longleftrightarrow \;\; (p) = P P' \tag{5}$

がわかります。

なぜ $\bmod{23}$ によって表せるかというと，二次拡大 $\mathbb{Q}(\sqrt{-23})/\mathbb{Q}$ がアーベル拡大で，クロネッカー・ウェーバーの定理より円分体 $\mathbb{Q}(\zeta_{23})/\mathbb{Q}$ に含まれるからです。円分体においては，ガロア群が

${\rm Gal}(\mathbb{Q}(\zeta_{23})/\mathbb{Q}) \simeq (\mathbb{Z}/23\mathbb{Z})^\times \tag{6}$

と同型になりますから， $(\mathbb{Z}/23\mathbb{Z})^\times$ の部分群によって分解法則が書けます。すなわち， $\bmod{23}$ で分解法則が表せるということです。

逆に， $(\mathbb{Z}/23\mathbb{Z})^\times$ の部分群を与えると，その部分群の類に属する素数が完全分解するような $\mathbb{Q}$ 上のアーベル拡大が一意に定まります（これを類体という）。

これこそが， $\mathbb{Q}$ 上の類体論でした。

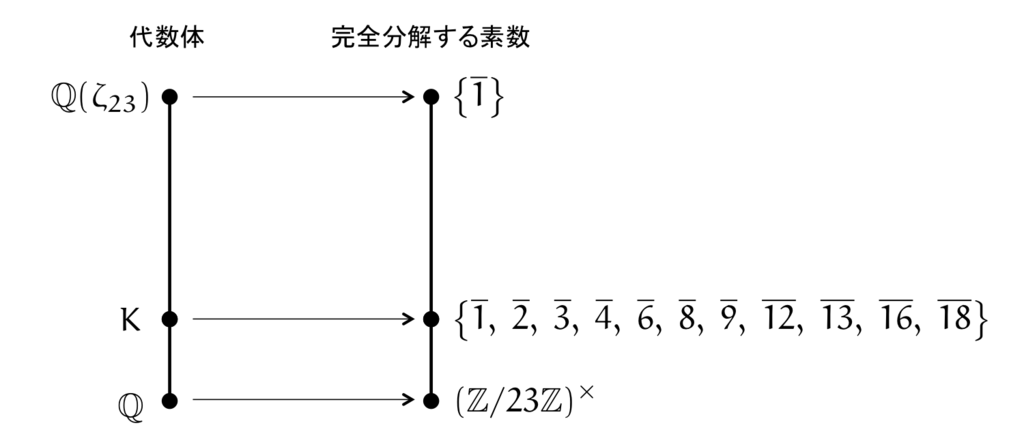
f:id:tsujimotter:20170123094701p:plain:w500

$\mathbb{Q}(\sqrt{-23})/\mathbb{Q}$ がアーベル拡大
円分体のガロア群が $(\mathbb{Z}/23\mathbb{Z})^\times$ に同型

の２点がキーであることを覚えておいてください。

分解法則は得られたわけですが，元の問題の解決にはまだまだ不十分です。

いくつか具体例を挙げてみましょう。

$p$	$(\mathbb{Z}/23\mathbb{Z})^\times$	素イデアル分解	$X^2 + XY + 6Y^2$
$2$	$\equiv 2 \pmod{23}$	$P_2 P_2'$ （単項イデアルではない）	表せない
$3$	$\equiv 3 \pmod{23}$	$P_3 P_3'$ （単項イデアルではない）	表せない
$5$	$\equiv 5 \pmod{23}$	惰性する	表せない
$7$	$\equiv 7 \pmod{23}$	惰性する	表せない
$11$	$\equiv 11 \pmod{23}$	惰性する	表せない
$13$	$\equiv 13 \pmod{23}$	$P_{13} P_{13}'$ （単項イデアルではない）	表せない
$17$	$\equiv 17 \pmod{23}$	惰性する	表せない
$19$	$\equiv 19 \pmod{23}$	惰性する	表せない
$23$	$\equiv 0 \pmod{23}$	$\left(-1 + 2\frac{1+\sqrt{-23}}{2}\right)^2$	$(-1)^2 + (-1)\cdot 2 + 6\cdot 2^2$
$29$	$\equiv 6 \pmod{23}$	$P_{29} P_{29}'$ （単項イデアルではない）	表せない
$31$	$\equiv 8 \pmod{23}$	$P_{31} P_{31}'$ （単項イデアルではない）	表せない
$37$	$\equiv 14 \pmod{23}$	惰性する	表せない
$41$	$\equiv 18 \pmod{23}$	$P_{41} P_{41}'$ （単項イデアルではない）	表せない
$43$	$\equiv 20 \pmod{23}$	惰性する	表せない
$47$	$\equiv 1 \pmod{23}$	$P_{47} P_{47}'$ （単項イデアルではない）	表せない
$53$	$\equiv 7 \pmod{23}$	惰性する	表せない
$59$	$\equiv 13 \pmod{23}$	$\left(5 + 2\frac{1+\sqrt{-23}}{2}\right)\left(5 + 2\frac{1-\sqrt{-23}}{2}\right)$	$5^2 + 5\cdot 2 + 6\cdot 2^2$

式 $(5)$ を満たす素数については，たしかに素イデアルの積に分解されています。

一方で，そのうち素イデアルが単項イデアルにならないケースにおいては，principal form の形に表すことができていません。

したがって，principal form で表せるための条件としては，式 $(5)$ では不十分というわけです。

一般の虚二次体の整数環においては，「単項イデアル環（すべてのイデアルが単項イデアル）」とは限りません。 $K = \mathbb{Q}(\sqrt{-23})$ も例にもれず，単項イデアル整域ではありませんので，分解された素イデアルが「単項イデアルかどうか」を気にする必要が出てきます。

もし単項イデアルに分解できれば principal form で表すことができますし，逆に principal form で表せるなら単項イデアルの積で表すことができます。principal form と単項イデアルは１対１に対応しています。

どういうことか説明しましょう。

もし， $P, P'$ が単項イデアルだった場合，

$\displaystyle P = \left(X + Y\frac{1+\sqrt{-23}}{2}\right)$

$\displaystyle P' = \left(X + Y\frac{1-\sqrt{-23}}{2}\right)$

と置くことができます。したがって，

$\displaystyle p = \left(X + Y\frac{1+\sqrt{-23}}{2}\right)\left(X + Y\frac{1-\sqrt{-23}}{2}\right) = X^2 + XY + 6Y^2$

と書くことができて，元の principal form になりました。

逆に，もし単項イデアルでないにもかかわらず $(p) = P P' = X^2 + XY + 6Y^2$ とかけたとすると，相異なる単項イデアル $(\alpha), (\alpha')$ によって

$(p) = PP' = (\alpha)(\alpha')$

とかけてしまうことになりますが，これは素イデアル分解の一意性に反します。したがって， $P, P'$ が単項イデアルでなければ $p = X^2 + XY + 6Y^2$ と書けません。

以上のことから， $P, P'$ が単項イデアルとなるような $p$ の条件を見つけたい，というモチベーションが出てきました。いったいどうすればいいのでしょう。

この問題は「ヒルベルト類体」を用いた「さらにもう一段上の類体論」を用いることで解決できます。

ところで「単項イデアルかどうか」という問題については， $\mathbb{Q}(\sqrt{-1}), \mathbb{Q}(\sqrt{-3})$ などの虚二次体では考える必要がありませんでした。類数が $1$ のため，すべてのイデアル類群の「類」が単項イデアルとなるからです。

$\mathbb{Q}(\sqrt{-5})$ の場合は，類数が $2$ なので，単項イデアルかどうか考慮する必要がありました。この場合は，ガウスの「種の理論」を用いることで解決できることを，以下の記事で示しました。
tsujimotter.hatenablog.com

$\mathbb{Q}(\sqrt{-23})$ の場合は，類数が $3$ となってしまいます。これが一層問題を難しくしています。この場合には，上の $\mathbb{Q}(\sqrt{-5})$ と同じようにはいきません。３つの類が同じ genus に含まれてしまうからです。

ちなみに $\mathbb{Q}(\sqrt{-23})$ は，類数が $3$ となる最初のケースです。こんな虚二次体が存在するおかげで，今回のような面白い問題が生まれたとも言えますね。

２．ヒルベルト類体における素イデアルの分解法則

ヒルベルト類体とは「最大不分岐アーベル拡大」という特殊なアーベル拡大のことです。基礎体 $K$ に対して，ヒルベルト類体 $L$ は一意に定まります。

「分岐」とは分解の指数が２次以上になることですが，「不分岐拡大」とは基礎体のすべての素イデアルが分岐しない（つまり不分岐）であるような有限次拡大のことです。

この拡大がイメージしづらいのは，基礎体 $K$ を $\mathbb{Q}$ として考えてしまうからでしょう。 $\mathbb{Q}$ の任意の有限次アーベル拡大においては，必ず有限個の分岐する素数を持ちます（たとえば， $\mathbb{Q}(i)/\mathbb{Q}$ において $2$ は分岐します）。 $\mathbb{Q}$ 上の真に大きな不分岐拡大はありません。つまり， $\mathbb{Q}$ の不分岐拡大は $\mathbb{Q}$ 自身のみです。

一般には，基礎体 $K$ と異なる不分岐拡大もありえて，しかもその拡大は複数ありえます。それらの不分岐拡大の中で，アーベル拡大かつ最大のものが「 $K$ のヒルベルト類体」というわけです。

今回考えたいのは， $K = \mathbb{Q}(\sqrt{-23})$ としたときのヒルベルト類体 $L$ です。 $\mathbb{Q}$ から $K$ まで持ち上げて，さらに $K$ から $K$ のヒルベルト類体 $L$ まで持ち上げるのです。

後で示しますが，この $K$ のヒルベルト類体まで持ち上げたときに「素数 $p$ が完全分解するかどうか」で「 $P$ が単項イデアルかどうか」がわかるのです。

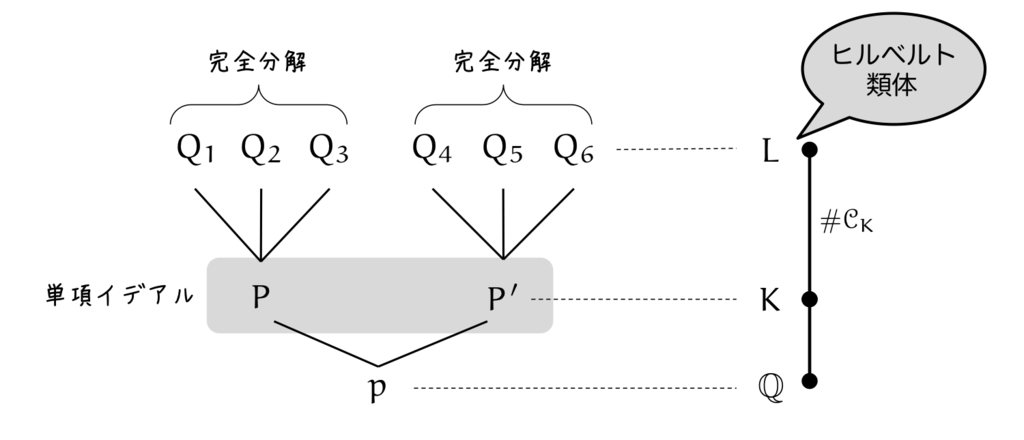
f:id:tsujimotter:20170122103352p:plain:w500

$K = \mathbb{Q}(\sqrt{-23})$ のヒルベルト類体 $L$ を実際に計算してみましょう。

伊藤先生の文章によると，きちんと計算するには「虚数乗法」と呼ばれる技術が必要だとか。今回はそこまで踏み込まず，Sage というソフトウェアで計算した結果を受け入れることにしましょう。

sage: K = NumberField(x^2 + 23, 'a'); K
Number Field in a with defining polynomial x^2 + 23
sage: L = K.hilbert_class_field('b'); L
Number Field in b with defining polynomial x^3 - x^2 + 1 over its base field

ヒルベルト類体が $L$ が求まりました。 $L$ は多項式 $X^3 - X^2 + 1$ の $K$ 上の分解体（ $X^3 - X^2 + 1$ が完全分解する体）となるようです。

訂正 (2016/01/22)：ヒルベルト類体の具体例に関する説明に私の勘違いがありましたので，訂正しました。

以降，基礎体を $K$ として， $K$ のヒルベルト類体 $L$ における分解法則から「単項イデアルを判定する方法」を導きたいと思います。

最大のポイントは，ヒルベルト類体においては「ガロア群」と「イデアル類群」が同型であるという事実です。この同型によって「単項イデアルとなる条件」が明らかになるのです。

定理

$L$ を $K$ のヒルベルト類体とする。すると，以下が成り立つ。

${\rm Gal}(L/K) \simeq \mathscr{C}_K \tag{7}$

ここで， $\mathscr{C}_K$ は $K$ のイデアル類群。

しかもこの同型写像は，具体的に以下の対応によって与えられます。

$\displaystyle \left(\frac{L/K}{\mathfrak{a}}\right) \longmapsto [\mathfrak{a}] \tag{8}$

$\mathfrak{a}$ は $K$ のイデアル。 $[\mathfrak{a}]$ は $\mathscr{C}_K$ における $\mathfrak{a}$ の属する類です。アルティンの相互法則といいます。

基礎体 $K$ の情報によって，拡大体 $L$ のガロア群が完全に決定されるという実に不思議なことが起きていることに注意してください。

類似の例を我々は知っています。円分体です。

円分体の同型定理は以下のものでした。

${\rm Gal}(\mathbb{Q}(\zeta_m)/\mathbb{Q}) \simeq (\mathbb{Z}/m\mathbb{Z})^{\times}$

さらに，この同型は以下の写像によって与えられることも説明しました。

$\displaystyle \left(\frac{\mathbb{Q}(\zeta_m)/\mathbb{Q}}{a}\right) \longmapsto [a]$

まったく同じ形になっていますよね。

類体論では「円分体」と「ヒルベルト類体」がより高いレベルで（具体的には「シュトラール類体」と呼ばれるものによって）まとめられるそうです。

さて，アルティンの相互法則を認めると，ヒルベルト類体における分解法則が得られます。ここで「素イデアルの分解」と「単項イデアル」が結びつきます。

素イデアル $P$ の $L/K$ における分解法則

$P$ が $K$ の単項イデアル $\;\; \Longleftrightarrow \;\; P$ が $L/K$ で完全分解

（ $\Longleftarrow$ ）完全分解するなら

$\displaystyle \left(\frac{L/K}{P}\right) = e$

が成り立つわけですが，アルティン相互法則により単項イデアル類 $[(1)]$ に対応します。

$\displaystyle \left(\frac{L/K}{P}\right) = e \;\; \Longrightarrow \;\; [P] = [(1)]$

したがって「 $P$ がヒルベルト類体 $L/K$ で完全分解するならば $P$ は単項イデアル」がわかります。

逆（ $\Longrightarrow$ ）も然り。

あっというまに分解法則が導けました。単項イデアルが完全分解と対応していますね。

群の同型写像によって「単位元（完全分解するフロベニウス）」が「単位元（単項イデアル類）」に結びつくという点が，証明のキーでした。アルティン相互法則によって「具体的な同型対応」が与えられたために，こんな素晴らしい結果が導けるのですね。

ヒルベルト類体の分解法則を具体例の計算によって確かめてみましょう。先ほどの Sage のコードの続きからはじめます。

まずは， $p = 59$ の場合です。 $p = 59$ においては， $(p) = PP'$ が $K$ において単項イデアルの積に分解されるので， $L$ においても完全分解するはずです。

sage: I = L.ideal(59); I
Fractional ideal (59)
sage: I.factor()
(Fractional ideal ((6/23*a + 1)*b^2 - 2/23*a*b + 5/46*a + 1/2)) * (Fractional ideal ((-1/46*a - 3/2)*b^2 + (4/23*a + 1)*b - 5/23*a + 1)) * (Fractional ideal ((-6/23*a + 1)*b^2 + 2/23*a*b - 5/46*a + 1/2)) * (Fractional ideal ((-13/46*a + 1/2)*b^2 + (6/23*a - 1)*b + 4/23*a + 1)) * (Fractional ideal ((1/46*a - 3/2)*b^2 + (-4/23*a + 1)*b + 5/23*a + 1)) * (Fractional ideal ((-13/46*a - 1/2)*b^2 + (6/23*a + 1)*b + 4/23*a - 1))

たしかに， $6$ 個の素イデアルの積に分解されていますね。

一方で， $p = 47$ の場合はどうでしょう。 $p = 47$ においては， $K$ において素イデアル分解されますが，単項イデアルにはなりません。したがって， $L$ では完全分解しないはずです。

sage: J = L.ideal(47); J
Fractional ideal (47)
sage: J.factor()
(Fractional ideal ((-6/23*a + 5)*b^2 + (27/46*a + 1/2)*b - 14/23*a - 4)) * (Fractional ideal ((-14/23*a + 4)*b^2 + (20/23*a + 1)*b - 27/46*a + 1/2))

$2$ 個の素イデアルの積に分解されただけで，完全分解（ $6$ 個の素イデアルの積）にはなっていませんね。 $p = 47$ は， $K/\mathbb{Q}$ で完全分解した後， $L/K$ で惰性したことがわかります。

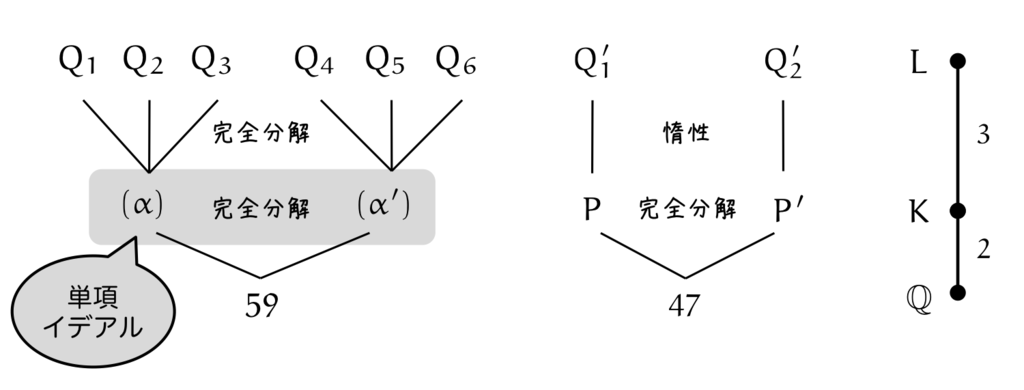
f:id:tsujimotter:20170122215841p:plain:w500

追記 (2016/01/22)：具体例の計算を追記しました。

以上をまとめると，

$p = X^2 + XY + 6Y^2$ でかける

という条件は，

$p$ が $K/\mathbb{Q}$ で完全分解して $p = P P'$
かつ
$P, P'$ は単項イデアル

だったわけですが，ヒルベルト類体 $L/K$ の分解法則によって

$p$ が $K/\mathbb{Q}$ で完全分解して $p = P P'$
かつ
$P, P'$ が $L/K$ で完全分解

と表せるようになったわけです。

もっといえば， $p$ が「 $K/\mathbb{Q}$ で完全分解して」さらに「 $L/K$ でも完全分解する」ということです。すなわち，

$p$ が $L/\mathbb{Q}$ で完全分解する

と言ってもいいわけですね。

したがって，我々は $L/\mathbb{Q}$ の分解法則に興味が出てきます。

３．非可換拡大における素イデアルの分解法則

それでは， $L/\mathbb{Q}$ の類体論を考えて，分解法則を計算しましょう。

といいたいところなのですが，これがそう簡単ではありません。

まず，これまでとまったく異なる状況が起きていることに注意してください。 $L/\mathbb{Q}$ はアーベル拡大ではないのです。すなわち，

${\rm Gal}(L/\mathbb{Q})$

は非可換なガロア群となっています。したがって，円分体のときと同じような議論を使うことができません。

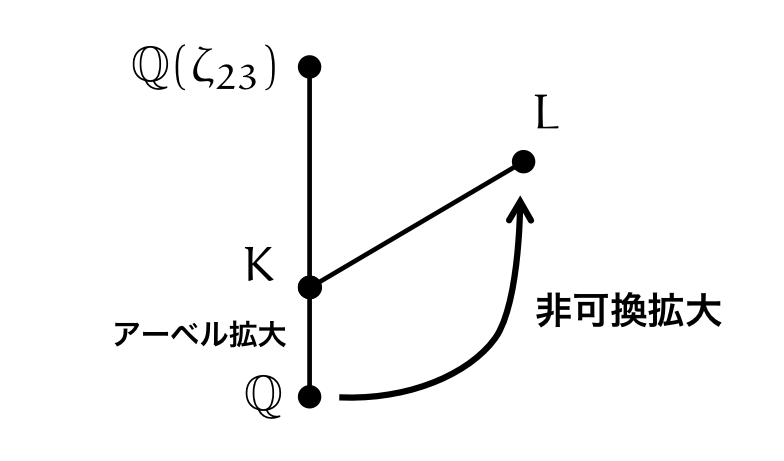
f:id:tsujimotter:20170122101533p:plain:w400

Sage を使って，実際に $L$ のガロア群を計算してみましょう。先ほどのコードの続きから始めます。

sage: G = L.galois_group("pari"); G
Galois group PARI group [6, -1, 2, "D_6(6) = [3]2"] of degree 6 of the Number Field in b with defining polynomial x^3 - x^2 + 1 over its base field
sage: G.order()
6

"D_6" と書いてありますが，これは位数が $6$ の二面体群 $D_3$ のことですね。"D_6" の "6" は位数の $6$ であって， $D_6$ の $6$ ではないことに注意です（ややこしい）。

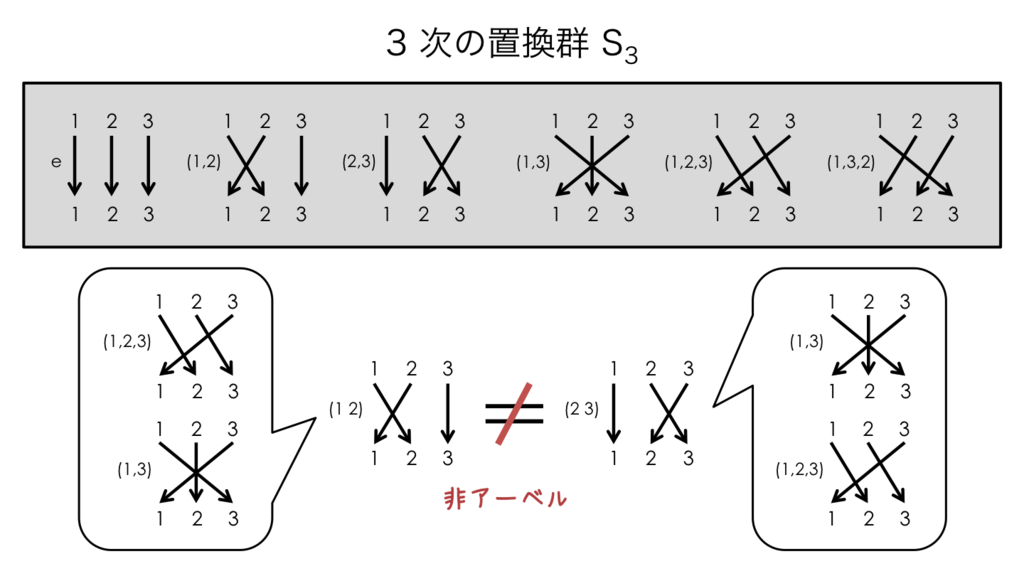
二面体群 $D_3$ は「正三角形の頂点を回転・反転させる対称な操作の群」のことです。 $6$ 通りの操作が存在して，これらの操作のなす群は $S_3$ と同型になります。

$S_3$ は「あみだくじ」でおなじみの「３つの要素を入れ替える群」，すなわち「３次の置換群」です。もちろん，以下に示すように $S_3$ はアーベル群ではありません。

f:id:tsujimotter:20170122100528p:plain:w500

訂正 (2016/01/22)：上記のヒルベルト類体の訂正に合わせて，ガロア群を計算し直しました。

フロベニウス共役類

非可換拡大においては，フロベニウス元が扱いづらくなるという弊害も現れます。

まず，フロベニウス元の定義を見直す必要があります。以下の記事で書いたフロベニウスの定義を思い返しつつ，アーベルでない場合を考えてみましょう。

tsujimotter.hatenablog.com

素数 $p$ が $L/\mathbb{Q}$ 上で，以下のように不分岐に分解するとします。

$(p) = Q_1 Q_2 \cdots Q_g$

このとき， $Q_1, Q_2, \cdots, Q_g$ のそれぞれに対して，分解群 $Z_{Q_1}, Z_{Q_2}, \cdots, Z_{Q_g}$ が定まります。不分岐なので，分解群 $Z_{Q_i}$ は巡回群となります。

また， $Z_{Q_i}$ にはフロベニウス自己同型 $\left[\frac{L/\mathbb{Q}}{Q_i}\right]$ という元が存在して，これによって生成できることが知られています。すなわち，

$\displaystyle Z_{Q_i} = \left\langle \left[\frac{L/\mathbb{Q}}{Q_i}\right] \right\rangle$

さて，もし $L/\mathbb{Q}$ がアーベル拡大であれば，ガロア群の可換性からそれぞれのフロベニウス自己同型は一致して

$\displaystyle \left[\frac{L/\mathbb{Q}}{Q_i}\right] = \left[\frac{L/\mathbb{Q}}{Q_j}\right]$

となることが示せます。

これについては以下の記事で示しました。
tsujimotter.hatenablog.com

一方で，今回のように $L/\mathbb{Q}$ が一般のガロア拡大，すなわちアーベル拡大でなければ，それぞれのフロベニウス自己同型は一致しません。したがって， $p$ によって定まるフロベニウス自己同型は，複数存在し

$\displaystyle \left(\frac{L/\mathbb{Q}}{p}\right) = \left\{ \left[\frac{L/\mathbb{Q}}{Q_1}\right], \; \left[\frac{L/\mathbb{Q}}{Q_2}\right], \; \cdots, \; \left[\frac{L/\mathbb{Q}}{Q_g}\right] \right\} \tag{9}$

という集合をまとめて考える必要があります。これを $p$ のフロベニウス共役類と呼びます。

こりゃあ大変だ。ずいぶん状況が変わってきますね。

一方で，こんな状況でも実はなんとかなるんです。その方法を以下で示すことにしましょう。

行列によるガロア群の表現

アーベル拡大においては，その拡大を含むような「大きな拡大体（円分体・ヒルベルト類体など）」を考えて，そのガロア群を「わかりやすい群（ $(\mathbb{Z}/m\mathbb{Z})^\times$ や $\mathscr{C}_K$ など）」に対応づけていました。非可換の場合においてもその方針は変わりません。

すなわち，今考えたい拡大を含むような「大きな拡大体」を考えて，ガロア群をより「わかりやすい群」に対応させるのです。

どんな拡大を考えるか
どんな群に対応させるか

という部分にセンスが問われるわけですね。

まず「どんな群に対応させるか」という問題ですが，ここでは「行列」によって，群を表現することを考えましょう。群を行列によって表現することはしばしば行われることで，その理論には「表現論」という名前が付いています。

ここでは，ガロア群 ${\rm Gal}(L/\mathbb{Q})$ を，以下の同型写像 $\rho$ によって，二次元行列 $GL(2, \mathbb{C})$ の群に埋め込むことにします。

$\rho \colon Gal(L/\mathbb{Q}) \simeq S_3 \hookrightarrow GL(2, \mathbb{C}) \tag{10}$

$\rho$ によって，フロベニウス共役類の元を

$\displaystyle \rho \colon \left[\frac{L/\mathbb{Q}}{Q}\right] \longmapsto \begin{bmatrix} a & b \\ c & d \end{bmatrix}$

のように二次元行列に対応させることができます。

あとは，この行列をみてフロベニウス共役類の振る舞いを観察すればよいわけです。

次に「どんな拡大を考えるか」ですが，ここで考えている「大きな拡大体」は， $\mathbb{Q}$ 上の任意の有限次拡大を施した親玉のような体 $\overline{\mathbb{Q}}$ です。すると， $\mathbb{Q}$ 上の任意の拡大は $\overline{\mathbb{Q}}/\mathbb{Q}$ に含まれることになります。このような拡大を「代数閉包（algebric closure）」といいます。

$\overline{\mathbb{Q}}/\mathbb{Q}$ に対するガロア群を考えると，

${\rm Gal}(\overline{\mathbb{Q}}/\mathbb{Q}) \hookrightarrow GL(n, \mathbb{C})$

のように $n$ 次元の行列に埋め込むことができることが知られています。 $L/\mathbb{Q}$ は $\overline{\mathbb{Q}}/\mathbb{Q}$ の部分体なので，自然とガロア群を行列に埋め込むことができるのですね。

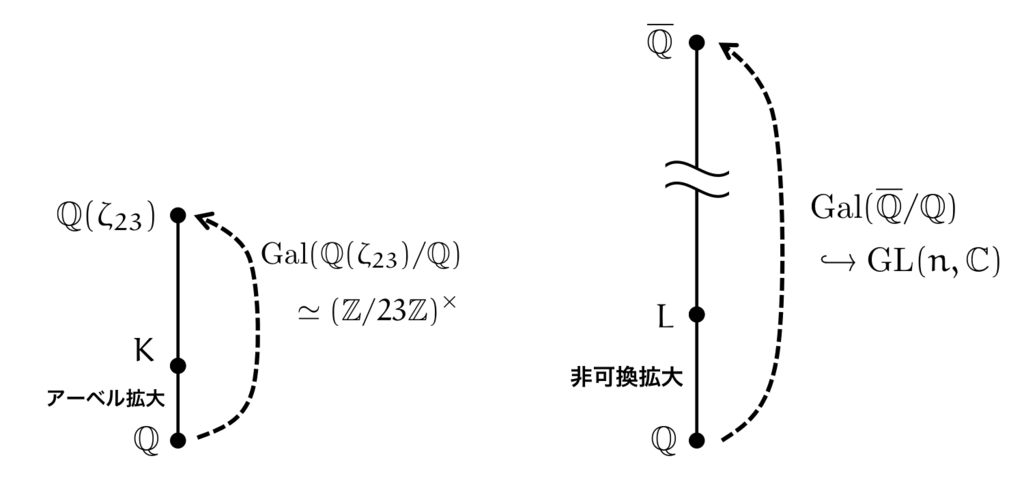
f:id:tsujimotter:20170122100232p:plain:w500

行列 $n$ の次元についてですが，たとえばアーベル群であれば１次元の行列（すなわち，単なる複素数）に埋め込めます。

一般に非可換な群であれば，２次元以上の行列が必要です。１次元では「非可換性」が表現できないからです。

伊藤先生の文献によると，二次体のヒルベルト類体は１次元または２次元の表現で十分なのだそうです。

理由はよく知りません。推測するに， $L/K$ のガロア群はイデアル類群というアーベル群に同型なので，これに二次拡大を乗せた群を考えると，必然的に範囲が限られるのではないかと思われます。

行列として表現することはもう一つ重大な理由があります。実は，

$(p) = Q_1 Q_2 \cdots Q_g$

によって定まる $p$ のフロベニウス共役類

をそれぞれ行列で表現したとき，そのトレースはすべて同じ値をとるのです。つまり， $\rho$ によって対応するフロベニウス共役類のつくる行列のトレースは，すべて同じ値を指します。

$\displaystyle {\rm Tr}\left(\rho\left[\frac{L/\mathbb{Q}}{Q_1}\right]\right) = {\rm Tr}\left(\rho\left[\frac{L/\mathbb{Q}}{Q_2}\right]\right) = \cdots = {\rm Tr}\left(\rho\left[\frac{L/\mathbb{Q}}{Q_g}\right]\right)$

これを単に

$\displaystyle {\rm Tr}\left(\rho\left(\frac{L/\mathbb{Q}}{p}\right)\right)$

と書くことにしましょう。

行列表現のトレースに着目することによって，フロベニウス共役類の違いを吸収して潰すことができるのですね。

すばらしい。なんとかなりそうな気がしてきました。

$S_3$ の指標表とトレース

それでは， $S_3$ が対応する行列を具体的に考えてみましょう。

実は，この行列はよく知られていて，インターネット上でも調べることができます。この対応関係は「指標表 (character table)」と呼ばれます。

たとえば「指標表」で検索すると，Wikipedia の記事が見つかります。

指標表 - Wikipedia

ここでは， $S_3$ の元が以下のように対応すると記されています。

$\begin{eqnarray} \displaystyle e &\longmapsto& \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \\ \displaystyle (1, 2) &\longmapsto& \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \\ \displaystyle (1, 2, 3) &\longmapsto& \begin{bmatrix} \omega & 0 \\ 0 & \omega^2 \end{bmatrix} \end{eqnarray}$

ここでは， $\omega = e^{2\pi i / 3}$ とおきました。

残りの元についても，適当に計算すればわかります。

$\begin{eqnarray} \displaystyle (1, 3) = (1, 2, 3)(1, 2) &\longmapsto& \begin{bmatrix} 0 & \omega \\ \omega^2 & 0 \end{bmatrix} \\ \displaystyle (2, 3) = (1, 2)(1, 2, 3) &\longmapsto& \begin{bmatrix} 0 & \omega^2 \\ \omega & 0 \end{bmatrix} \\ \displaystyle (1, 3, 2) = (1, 2, 3)(1, 2, 3) &\longmapsto& \begin{bmatrix} \omega^2 & 0 \\ 0 & \omega \end{bmatrix} \end{eqnarray}$

さて，我々が知りたいのは，この行列のトレースでした。すなわち，対角の和を計算すれば良いわけです。

まず，単位行列 $\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$ については，

${\rm Tr}\left( \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \right) = 2$

がわかります。

また，そのほかの行列についても，

$\begin{align} {\rm Tr}\left( \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \right) &= 0 \\ {\rm Tr}\left( \begin{bmatrix} \omega & 0 \\ 0 & \omega^2 \end{bmatrix} \right) &= -1 \; (= \omega + \omega^2) \\ {\rm Tr}\left( \begin{bmatrix} 0 & \omega \\ \omega^2 & 0 \end{bmatrix} \right) &= 0 \\ {\rm Tr}\left( \begin{bmatrix} 0 & \omega^2 \\ \omega & 0 \end{bmatrix} \right) &= 0 \\ {\rm Tr}\left( \begin{bmatrix} \omega^2 & 0 \\ 0 & \omega \end{bmatrix} \right) &= -1 \; (= \omega^2 + \omega) \end{align}$

が計算できます。

我々が知りたいのは， $p$ が完全分解する条件だったわけですが，これはフロベニウス共役類がそろって単位元になるときです。また，行列の表現によって，単位元は単位行列に移されます。

一方で，行列のトレースがフロベニウス共役類の取り方によらず定まるということは，逆にトレースの値から $p$ が完全分解する条件がわかるということです。

指標表に示された行列の計算からわかったことは，トレースの値が $2$ であるのは，

単位行列だけ

であるという事実です。このことから，以下の分解法則が得られます。

$p$ が $L/\mathbb{Q}$ において完全分解する $\displaystyle \;\; \Longleftrightarrow \;\; {\rm Tr}\left(\rho\left(\frac{L/\mathbb{Q}}{p}\right)\right) = 2 \tag{11}$

やったー！

$a_p = 2$ という条件にあった $2$ という数が出てきましたね！

あと一歩です！

保型形式とガロア表現

最後に，ざっくりとですが「トレースが保型形式と結びつく理由」を説明します。

結論からいうと， $p$ 次のフーリエ係数 $a_p$ が

$\displaystyle {\rm Tr}\left(\rho\left(\frac{L/\mathbb{Q}}{p}\right)\right) = a_p \tag{12}$

を満たすような保型形式 $f$ が存在して，その保型形式が

$\displaystyle f(\tau) = \sum_{n=1}^{\infty} a_n q^n = q\prod_{n=1}^{\infty} (1-q^n)(1-q^{23n}) \tag{再掲1}$

のようにかけるのだそうです。これは一般的に言えることのようです。

伊藤先生の文章を引用しましょう。

一方で，定理4.1の保型形式 $f$ は尖点形式で，ヘッケ作用素の同時固有形式なので， $f$ に伴うガロア表現が存在する．すなわち，既約な２次元ガロア表現
$\rho_f \colon {\rm Gal}(\overline{\mathbb{Q}}/\mathbb{Q}) \longrightarrow GL(2, \mathbb{C})$
であって， ${\rm Tr}\;\rho_f({\rm Frob}_p) = a_p$ を満たすものが存在する．実は，この $\rho_f$ が $\rho_{H/\mathbb{Q}}$ と同値であるというのが，定理4.1の「種明かし」である．

保型形式には，どうやらそれに付随する「ガロア表現」というものが存在して，それが

$\rho_f \colon {\rm Gal}(\overline{\mathbb{Q}}/\mathbb{Q}) \longrightarrow GL(2, \mathbb{C})$

というガロア群の行列による表現を定めているようなのです。

「固有形式」や「尖点形式（カスプ）」という条件もついているみたいですが，このような条件を満たす固有形式は，今回示したようなガロア表現を持つようです。

実際，今回紹介した式 $(1)$ の保型形式 $f$ は，条件を満たし

$\displaystyle {\rm Tr}\left(\rho\left(\frac{L/\mathbb{Q}}{p}\right)\right) = a_p$

が成り立つのだそうです。

そんなことが成り立つ保型形式が存在するというのがすごいですね！

同様の記述をほかの本でも見つけたので紹介します。

定理 A.1（Deligne-志村，Ribet） $f \in S_k(\Gamma_1(M))$ を重さ $k \geq 2$ の正規化された固有カスプ形式， $K$ を $f$ の $q$ 展開の係数を全て含む $\mathbb{Q}_p$ の有限次拡大体とする．このとき， $2$ 次元 $K$ ベクトル空間 $V_f$ への連続なガロワ表現 $\rho_f\colon G_{\mathbb{Q}} \longrightarrow {\rm Aut}_K V_f \simeq GL_2(K)$ で，次をみたすようなものが存在する：
(i) $V_f$ は $pM$ を割らない $\mathbb{Q}$ の素点では不分岐．
(ii) $pM$ を割らない勝手な素数 $l$ での幾何的フロベニウス元 $Frob_l \in G_{\mathbb{Q}}$ に対して， ${\rm Tr}\; (\rho_f(Frob_l)) = a_l(f)$ となる．
(iii) $V_f$ は $G_\mathbb{Q}$ の表現として既約．
（落合理「岩澤理論とその展望（上）」p.163 より引用）

該当箇所は，(ii) の部分ですね。この定理は Deligne と志村先生によって示されているそうです。また，上記の本には以下のようにも書かれています。

(ii) は定理の中で最も深い記述であり，フロベニウスから定まる代数対応と Hecke 作用素から定まる代数対応を比較する，所謂「合同関係式」からなる．

とのこと。このへんがきちんと理解できたらとても楽しそうですね。

ともかく，今回の問題に限って言えば，保型形式に関する以上の結果を受け入れると「保型形式の $a_p$ がフロベニウス共役類のトレースと対応付く」ということが説明できると私は理解しました。

まとめ

今日は

$p = X^2 + XY + 6Y^2$

という二次形式でかける素数の条件が，保型形式のフーリエ係数 $a_p$ でかけるのは一体なぜだろうか，という話でした。

この仕組みを理解するためには，これまで扱ってきたように単純な $\mathbb{Q}$ 上の類体論のみならず，

さらにもう一段上の $K$ 上の分解法則（ヒルベルト類体）
非可換拡大における分解法則

を必要とすることを述べました。こんなにも奥の深いトピックだったのですね。

一通り説明するために，ずいぶんと長い記事になってしまいました。最後にポイントを振り返りつつ，話の流れをまとめてみましょう。

まず第１部では，二次体 $K = \mathbb{Q}(\sqrt{-23})$ に着目し， $\mathbb{Q}$ 上の類体論から素イデアル分解法則を導きました。これにより，

$p \equiv 1, 2, 3, 4, 6, 8, 9, 12, 13, 16, 18 \pmod{23} \;\; \Longleftrightarrow \;\; p$ が $K$ で完全分解する

という条件を導くことができ，なおかつ分解された素イデアルが単項イデアルであれば，目的の $X^2 + XY + 6Y^2$ でかけることを示しました。

次に第２部では，単項イデアルとなる条件を導くために，ヒルベルト類体 $L$ まで持ち上げて，そこでの分解法則を考えました。結果，

$p = X^2 + XY + 6Y^2 \;\; \Longleftrightarrow \;\; p$ が $L/\mathbb{Q}$ で完全分解する

という結論を得ました。

第３部では， $L/\mathbb{Q}$ 上での分解法則を考えたいが，非可換拡大ゆえの困難（円分体の分解法則が使えない・フロベニウス共役類など）が伴うことを指摘しました。これについては，ガロア群を行列によって表現することで，そのトレースが「フロベニウス共役類によらず一意に定まること」を利用して解消できることを説明しました。群の指標表の観察により，

$\displaystyle p = X^2 + XY + 6Y^2 \;\; \Longleftrightarrow \;\; {\rm Tr}\left(\rho\left( \frac{L/\mathbb{Q}}{p} \right)\right) = 2$

という結論を得ました。

最後に，フロベニウスのトレースをフーリエ係数 $a_p$ に持つ保型形式が存在すること，そしてそのような都合の良い保型形式が実は式 $(1)$ の $f$ であったということに触れました。

$\displaystyle f(\tau) = \sum_{n=1}^{\infty} a_n q^n = q\prod_{n=1}^{\infty} (1-q^n)(1-q^{23n}) \tag{再掲1}$

結果として「保型形式」と「今回の二次形式の問題」が無事つながることを示すことができました。

考えるべきポイントが多々あって，非常に面白い問題だったのではないでしょうか。まさにこれまでの勉強の集大成という感じでした。

個人的に特に面白かったのは，非可換の世界を記述するために「行列」という「積が一般に非可換になる道具」が使えるということです。高校のときに習った「行列」ですが，あれはいったいなんだったのかと当時は思ったものです。実は，行列が「非可換の世界」に触れる初めての体験になっていたわけですね。面白い。

最後の「保型形式のガロア表現」についての話は，これからも継続して調べたいトピックですね。「虚数乗法」に基づいてヒルベルト類体を構成する方法についても，まだよくわかっていません。

単純に抽象的な理論を掘り下げて勉強していくのも面白いですが，tsujimotterとしては，今回のような「具体的な問題設定」がありつつ，その問題の背景を理解するためには実は深い抽象的な理論が必要である，という話に心惹かれます。二次形式の話は，まさにそんな魅力を持った話なのだと思っています。

それでは，最後まで読んでくださってありがとうございました！

参考文献

伊藤哲史「平方数の和で表される素数について」城咲新人セミナー
~~https://www.math.kyoto-u.ac.jp/insei/proceeding/2010/ito.pdf~~
https://drive.google.com/file/d/1RrC0WG676Hv3k2W0pfK6LY00hiC0kaR0/view
（リンク先が変わりました）

ヒルベルト類体のあたりのイメージはこちらの本がとても参考になりました。