今日考えたい問題は という二次形式で書ける素数の法則です。実際,
という法則が知られており, の素イデアル分解によって説明できます。これについて,以前の記事でまとめたことがありました。
tsujimotter.hatenablog.com
一方で,上の記事では「たまたまそういう条件のときに と書ける」程度の説明となっており「なぜそのような法則が得られるか」という根拠がまったくわかりませんでした。
今日は「ガウスの種の理論」によってこの根拠を説明します。種の理論は「指標」という概念を用いて二次形式やイデアル類群を分類しようという試みです。
種の理論は,単に上記の法則の説明を与えるにとどまらず,もっと一般的に二次形式で表せる素数の条件についてザックザクと法則を導くことができます。魅力的なトピックです。
しかしながら,やや難解で抽象的な議論が続くことになります。私もずっと理解したいと思っていたのですが,難しくてこれまで理解することができませんでした。数日前にこの記事に書いた理解に到達できたという状況です。
抽象的な内容を理解しやすいよう,可能なかぎり具体的例を用いて考えていきたいと思います。後半にたくさん二次形式の例が登場します。いろいろ遊ぶことができますので,辛抱強く読んでもらえると嬉しいです。
背景の説明(少し長め)
上に述べたように,種の理論のキーポイントは「素数を「指標」によって分類する」というアイデアです。このアイデアを理解するために,指標についてのお勉強から入りたいと思います。ちょっと長いですが,大事なパートなのでじっくり導入していきます。
指標の定義
まず「指標とは何か」というあたりから説明しましょう。
今回紹介する指標は,任意の整数に の値を割り当てるルールです。二次体
の判別式を
としたとき,
を用いて
と表し,これを「二次体
に付随する法
の指標」と呼びます。
さて,この指標 を以下のように定義しましょう。
まず,二次体
判別式 と素数
に対して,指標
を以下に定めます。
と定義します。 はヤコビ記号です。
と素因数分解すれば,
とルジャンドル記号を用いて表せます。
一般の に対しても,
の素因数分解を用いて指標
を定義できます。すなわち,
と書けるとき
と定義することができます。
なんだこのややこしい定義は,と思ったかもしれません。
たとえば,上記のコードの最後に
d = -20 a = 9 puts chi(d, a)
と打ってあげれば,
であることが計算できます。
こんな風に「とてもややこしい式」によって定義される指標ですが,非常に便利な代物なのです。
何が便利かというと,たとえば二次体 における素イデアルの分解法則がこれを使ってかけてしまうんです。
おお,なんか便利そうですね!
まぁ,便利そうというか,二次体の分解法則の難しい部分を,先ほどのややこしい定義によってがんばって表現したもの思えば,それほど不思議ではないかもしれません。
今回はこの指標が主役です。

指標 の重要な特徴を1つ指摘しておきましょう。この指標は「群準同型」になっています。群準同型とは,群から群への写像になっていて,群の積の構造を保つという性質をもった特別な写像のことでした。
どういう群の写像になっているか考えてみましょう。
が奇素数のときの場合わけを考えると,平方剰余の記号が入っています。ここで平方剰余の相互法則を用いると,
がひっくりが返って,結局
は
にしかよらないことがわかります(ぜひ考えてみてください)。
また, を割り切る素数
に対しては
を,そうでないときには
を返すこともわかります。したがって,
と互いに素な元だけを考えると,
を返す写像になっています。
したがって, は
という写像と見なすことができるでしょう。
と
はそれぞれ乗法に対して群をなします。指標の定義から明らかに以下が成り立ち,群の積を保つことがわかります。
ここで, です。
したがって,群 の準同型写像と見なせます。
一般の群の元に対して, の値を割り当てる準同型写像のことを,群指標と呼ぶそうです。これが「指標」という言葉の由来だったわけです。
 に戻って考える。
に戻って考える。
さて,冒頭の問題に戻ってみましょう。
における素イデアルの分解法則を考えると,判別式は
より,
が成り立ちます。
具体的に の値を計算してみましょう。
が奇素数のとき
であることが定義からわかるので, のそれぞれの指標の値を考えればよいことがわかります。
まず, の方は
という変形できます。最右辺は平方剰余の第一補充則の形をしているので,これを適用すると
のとき
のとき
がわかります。
一方, の方ですが,平方剰余の相互法則より
がわかるので,
のとき
のとき
がわかります。
結局2つの指標をまとめると, と
の2つの条件は
の条件で表すことができて *1
が得られます。
このようなときに が完全分解するというわけです。まとめると以下の法則が得られました。
ここで, は共役な
の素イデアル。
もし が単項イデアルであるとします。
とかくと
として,二次形式 の形で表せる素数の形式に持っていけます。
一方で, の類数は
ではないので,
が単項イデアルとは限りません。すなわち,
でかける素数の法則は,
だけではまだわからないのです。
どうにかして が単項イデアルになる条件を知りたい,というのが今日のお話です。
ガウスは
という。
ガウスかっこいい。
長くなりましたが,以上が今日のお話のモチベーションです。果たしてガウスはどんな方法で解決したのでしょうか。
種 (genus) の理論
いよいよガウスの種の理論の説明です。
ガウスが考えたのは,指標を 素判別式 で分解するというアイデアです。
素判別式
先ほどの の議論で,
と分解してから,それぞれの指標を計算していました。この と
は素判別式と呼ばれるものです。
素判別式を定義する前に,それぞれの指標の値をもう一度整理してみましょう。
| 素数の条件 | ||
|---|---|---|
完全分解する素数の類が,分解された指標の値の組みによって,さらに2つに分類できました。
ここで面白いのは,
には際立った特徴があるということです。 を
で素イデアル分解したとき,その分解を
と表すと,素イデアル
は なんと必ず単項イデアルになるのです!
な,なんだってーーー!!??
さぁ,これで俄然,指標を分解したくなってきました。
素判別式は,以下のように定義します。
先の例で言うと, は素判別式ではありませんが,
は素判別式です。たしかに
のように は素判別式の積で表せることが確認できます。
genus の定義と驚くべき性質
ガウスの種の理論では,素判別分解した指標によって「イデアル類群」を分類します。
突然「イデアル類群」が出てきたので「ん?」と思った方もいるかと思いますので,先の例を使って少し補足します。
で完全分解される素数は,単項イデアルに分解されるかどうかで二種類に分けられるのでした。単項イデアルに分解される素数を
,そうでない素数を
として以下のように表記します。
このとき, は単項イデアルで,
はそうではありません。
また, のイデアル類群
の位数は
ですから,
の属する類をそれぞれ
と書くと,以下のように表せます。
このようなイデアル類群の分類を, の指標の値だけを使ってやってしまおうというわけです。そんなことができてしまうのでしょうか。次の図のようなイメージです。
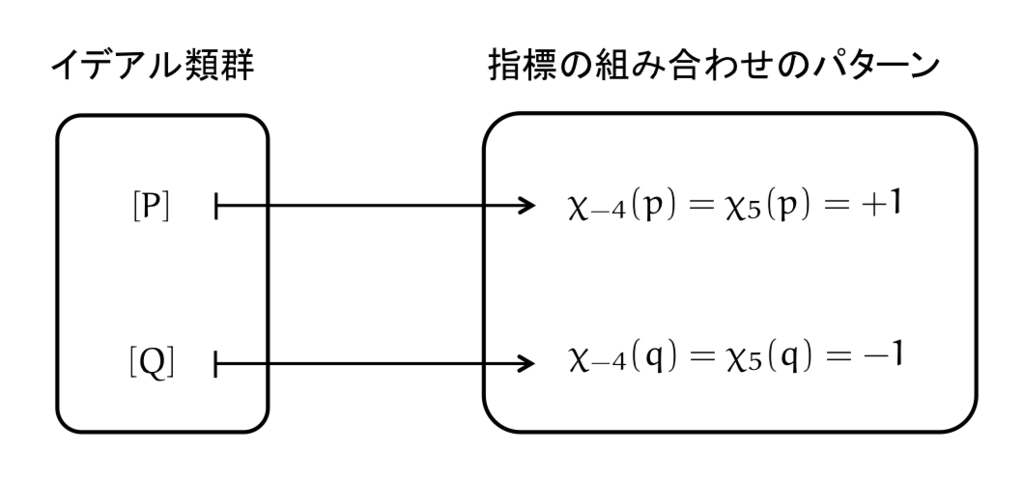
指標が同じ値をとるイデアル類群の集合を genus といいます。上の例で言うと, がそれぞれ1つの genus です。
実際,genus によってイデアル類群が分類できる,という思想を実現するのが
です。
それでは,先ほどの の例を思い浮かべながら,次のような写像を考えましょう。
また,素数 が
上で
と完全分解されるとする。このとき,素判別式
から
個を選んで,それぞれの指標の組を並べたものを値に持ち,
を変数とする写像
を考える。
このように定義した からの群準同型写像
が存在する。
写像 のイメージが掴みづらいかもしれないので,図を使って説明を試みましょう。
まず,右辺は のいずれかを取る指標の値を
個並べた組になっています。
の変数はイデアル類群
の元です。
から指標のとりうる組み合わせ
に対して,図に示すような写像が構成できるのです。

このような対応関係が「写像になっている」つまり "Well-defined" ということは,イデアル類群の元を指標によって「分類」できることを意味しています。
なぜなら は類ですから,
に同値なたくさんのイデアルが集まってできています。本来はそのたくさんの集まったイデアルそれぞれに,別々の指標の値が割り当たってもいいはずなのですが,なぜかイデアル類ごとに同じ値をとるということを主張しているのです。これが Well-defined の意味するところです。
今回は証明しませんが,この Well-defined 性は実際に成り立っています。
もっと言うと は準同型写像になっています。
を考えれば(指標の値が
となるようなイデアルの類の集合のこと),イデアル類群
を
で割った剰余類系が,イデアル類群の分類そのものになります。
これはまさに準同型定理のことですね。このようにうまいこと表現できるのは,もともとの が群準同型だからです。
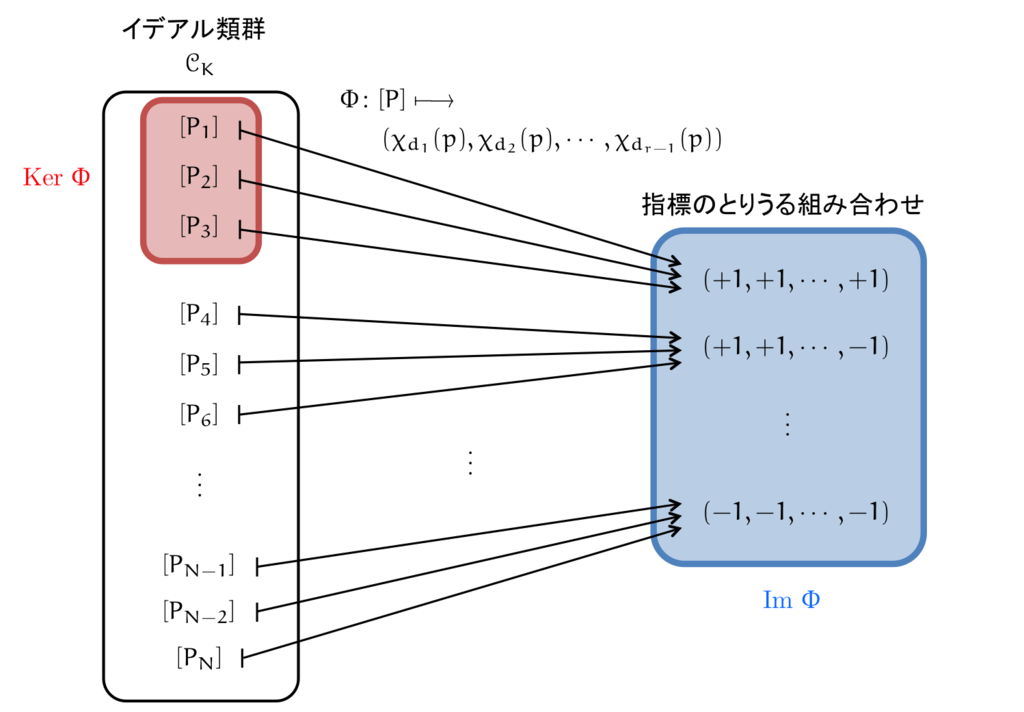
,すなわち,
によって単位元
に対応する類を principal genus といいます。
このように記述すると,genus を「イデアル類群を principal genus で割った剰余類」として定義できます。また,この剰余類系を genera といいます("genera" という単語は genus の複数形ですね)。

genus の具体的な構造
あとは と
がわかれば,イデアル類群について相当な情報が特定できてしまうわけです。
まず少なくとも, すなわち principal genus には必ず単項イデアルが入っています。それは,
が群準同型であることからわかります(単位元は単位元に移す)。単項イデアルは英語で principal ideal なわけですが,principal genus という名前の由来はここにあったわけですね。
一般に principal genus は単項イデアルのほかにも入っていますが,もし単項イデアルだけしか入ってなければ,指標から単項イデアルかどうかが判定できてしまいます。
これはすごい!
ここで,principal genus の構造が気になるわけですが,都合の良いことに principal genus の構造は具体的にかけてしまうんです!これ,すごいことでしょう!!
実際,以下が成り立ちます。
このとき,前述の に対し以下が成り立つ。
なんと,principal genus がイデアル類群の元を二乗してできた部分群によって,わかりやすく記述できるというのです。この辺のすごさは,具体的に計算してみるとよーく実感できると思います。
とはいえ,なんで判別式を割る素数で分解できたり, が principal genus になったりするのかが謎だと思いますが,これは二次拡大の分岐に関係があるそうです。詳しくは知らないので解説できませんが,非常に興味深いですね。
今日はガウスに感謝しつつ結果を受け入れて,具体例を計算することにしましょう。
素判別式分解すると 個の指標ができます。この素判別式における指標を分類すると,
通りのパターンが生まれます。
一方で,そもそも今回考えている対象は,素イデアル分解できる素数だったことを思い出しましょう。完全分解する条件を思い出すと,指標を掛け合わせると にならなければなりません。
したがって, 個の指標の値が決まると,残り
つの指標の値は自動的に決まってしまうのです。自由度が1つ減るということですね。
だから になるわけです。
種の理論によって  の例を解決
の例を解決
としたとき,判別式は
と素判別式分解できました。ということは,素判別式の個数は です。
ここで,素判別式における指標 を用いて,
を定義しましょう。
より,どちらか一方を用いればよいです。今回のケースでは,
と定義してもいいですし,
としてもいいです。どちらを選んでも
は前提となっているからです。
さて,principal genus は となる
の条件ですから
となり,これらのうちいずれかの類が単項イデアルになります。果たしてどの類が単項イデアルになるのでしょうか。
種の理論によると principal genus は で書けるということですから,
を実際に計算しましょう。
は二次の巡回群でした。したがって,すべての元の位数が
となります。つまり,
は単位元しか残りません。
の単位元は,単項イデアル全体の類ですから principal genus にいる元はすべて単項イデアルであることがわかります。
以上により,
のすべての素数は,単項イデアルに分解されることがわかりました。実は,全部単項イデアルだったのです。
まるで魔法のようでしょう!
今の例のように,もし が二乗して消えるなら単項イデアルが完全に特定できるし,そうでなくても
の構造が具体的に特定できるんです。
たとえば,素判別式の個数が 以上のとき,類数が
のべき乗で割り切れることがわかります。
理由を説明しましょう。群論のラグランジュの定理から,
が成り立ちます。
より, がわかり,結果としてイデアル類群の位数が
で割り切れることがわかります。
つまり,素判別式の個数から類数が 以上であることが確定するんです。すごいなこれ。
虚二次体のいくつかの例
種の理論のパワーをもっと知ってもらうために,虚二次体の具体例をいくつか計算してみましょう。
素判別式とその個数,類数の値を並べてみましょう。類数は,以下のサイトからとってきました。
integers.hatenablog.com
| 素判別式 | 類数 | 備考 | |||
|---|---|---|---|---|---|
| 例2 | |||||
| 例1 | |||||
のときは,類数が
以上になっていることを確認してみてください。
たとえば, のときは,判別式
と素判別式分解できますから,
です。したがって類数が
以上であることがただちにわかります。
実際,類数が ですから principal genus は単項イデアルだけになります。したがって,
となる条件で,二次形式
で表せる法則が記述できます。具体的に指標を計算すると
がわかります。
また,類数がわかっていれば(幸い小さい方の類数はよく知られている)イデアル類群のかなり多くの情報を知ることができます。そのことを,類数が同じだけれどイデアル類群の構造が異なる2通りの例を計算することで説明しましょう。
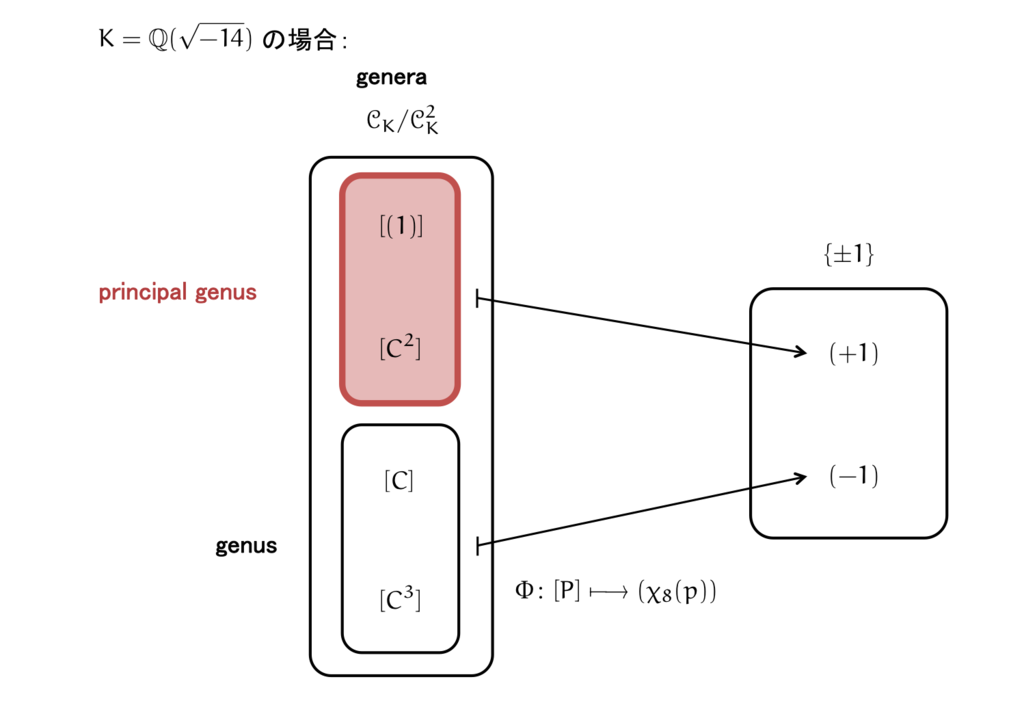
例1: の場合:
の場合:
まず, の判別式を計算すると,
は
で割って
あまる数なので
となります。この判別式には,以下の素判別式分解があります。
よって, です。ということは,種の理論より
がわかります。右辺の位数が なので,
の位数は
となります。
一方, の類数は 4 ですから
より ,すなわちイデアル類群は2乗するとすべての元が消えることがわかります。つまり,イデアル類群
の任意の元の位数は
か
であることがわかります。
位数 の群は2種類存在しますが,以上の条件を満たすのは1つだけ,クラインの四元群です。
実際,高木先生の初等整数論講義(の巻末付録)によると,イデアル類群 は以下の4つの類で構成されます。
- 単項イデアルを含む類
- イデアル
を含む類
- イデアル
を含む類
- イデアル
を含む類
すなわち,以下のように書けます。
これは,まさにクラインの四元群になっています。
乗算表は以下のとおり。
それぞれの元の位数を考えると,
の位数は
の位数は
となりますから, 乗するとすべて単位元となります。したがって,principal genus
は単項イデアルのみとなりますね。

イデアル類群の構造がわかりましたから,次は素イデアルの分解法則について考えましょう。
を素数とし
を計算すると,
のように分解法則が表せます。
しかし,このままでは が単項イデアルかわかりません。principal genus によってさらに細かく分類しましょう。
ここで,
となる の条件は,
であることがわかります。これより,principal genus に含まれる に分解される
の条件がわかりました。
一方,先のイデアル類群の構造の議論より principal genus の位数は です。すなわち,単項イデアルしかありませんから,この条件の素数はすべて単項イデアルの積によって得られる二次形式でかけます。よって
という法則が得られました。
実際,たとえば として,
ですが,
が成り立ちます。
例2: の場合:
の場合:
次に のケースを考えましょう。
の判別式を計算すると,
は
で割って
あまる数なので
となります。この判別式には,以下の素判別式分解があります。
よって, です。ということは,種の理論より
がわかります。右辺の位数が なので,
の位数は
となります。
一方, の類数は 4 です。先ほどのケースと異なるのは,類数と
の位数が一致しないという点です。つまり
より, となって,principal genus が潰れません。
位数4の群で,二乗して消えない元を持つのは,四次の巡回群です。またまた具体的に群の構造がわかってしまいました。
実際,これまた初等整数論講義(この本便利ですね)によると,イデアル類群 は以下の4つの類で構成されます。
- 単項イデアルを含む類
- イデアル
を含む類
- イデアル
を含む類
- イデアル
を含む類
すなわち,以下のように書けます。
これは,まさに四次の巡回群になっています。
乗算表は以下のとおり。
それぞれの元の位数を考えると,
の位数は
の位数は
の位数は
となりますから,位数が 2 より大きい元が存在します。したがって, 乗して単位元にならない元が存在するので
は非自明になります。具体的には
となります。つまり,principal genus には単項イデアルではない類も含みます。
もう随分と状況が変わってきましたね!
さて,素イデアル分解法則も考えましょう。
を素数とし
を計算すると,
のように分解法則が表せます。しかし,例によって が単項イデアルかわかりません。
ここで,素判別式から
となる の条件を考えると,
であることがわかります。これより,以上の素数を分解すると,その素イデアル は principal genus に含まれることがわかりました。
あとは が単項イデアルかどうかですが,残念ながらこのケースでは,単項イデアルかどうか,指標だけでは判断できません。principal genus に単項イデアルでない類も含まれるからです。
したがって以上の結論をまとめると,
であれば, の素イデアル
は,単項イデアルであるか
の類に含まれるかのいずれかとなる。
少し気持ち悪いですが,種の理論でわかるのはこれが限界です。
実際,単項イデアルで表せると の形で書けるわけですが,
の類に入るケースでは
という形の二次形式になってしまいます。つまり,
が成り立つというわけです。右辺の2つの二次形式のどちらが選ばれるかは,指標からは区別しようがありません。
種の理論で単項イデアルかどうか判別できるのは,先の例のように が自明群に潰れるとき,すなわち principal genus が単項イデアルだけになるときだけなのですね。
まとめ
今日は,指標をつかってイデアル類群を分類するというガウスの種の理論をご紹介しました。
種の理論によって,類数が でない場合においても、単項イデアルに属する素イデアルが具体的に決定できて,二次形式
でかける法則をたくさん導くことができました。今日だけで3つも法則を見つけることができました。
tsujimotter は二次形式でかける素数を可視化するプログラムを公開していますが,今回のようなやり方で法則を増やしていけば,たくさんの例をつくることができて楽しいです。そのうち,以下のページをもっとパワーアップさせたいと思います。
tsujimotter.info
種の理論は非常に強力な道具です。そのアイデアの根幹は,指標を素判別式で分解して,それぞれの値が同じ組を genus としてグルーピングすることにありました。さらに,その割り当ては群準同型となっているので,うまく構造を保つことができて,principal genus だけを見れば,全体の genus がどのように分かれているのかがよくわかるというわけです。
さらに,principal genus はイデアル類群を二乗してできた部分群 になることが知られていて,これによってイデアル類群の構造も具体的にわかってしまう。また,例1のように,イデアル類群を二乗してすべて消えるのであれば,principal genus は単項イデアルだけになるので,二次形式の法則が完全にわかるというわけでした。
ところで,今回は単項イデアル(principal ideal)で作られる という形の二次形式(
であれば
)に着目しました。このような二次形式のことを principal form というそうです。今回の話を二次形式の言葉で言い換えると,
を表す二次形式が principal form で表せる条件が,指標によって表せるかという問題だったわけです。ガウスの時代には,イデアルという概念は無かったので,純粋に二次形式で考えていたわけです。
一年くらい前から,tsujimotter は二次形式の話にこだわって整数論を勉強してきましたが,それにしても奥が深い分野ですね。実は,私がまだ紹介しきれていない面白い理論が背景には潜んでいます。そのうちこのブログでも書いていけたらと思います。
それでは,今日はこの辺で。
長文を最後まで読んでくださってありがとうございました。
関連記事
参考文献

- 作者: 青木昇,飯高茂,中村滋,岡部恒治,桑田孝泰
- 出版社/メーカー: 共立出版
- 発売日: 2012/12/21
- メディア: 単行本
- 購入: 2人 クリック: 2回
- この商品を含むブログを見る

- 作者: 高木貞治
- 出版社/メーカー: 共立出版
- 発売日: 1971/10/15
- メディア: 単行本
- 購入: 2人 クリック: 39回
- この商品を含むブログ (19件) を見る

- 作者: David A. Cox
- 出版社/メーカー: Wiley
- 発売日: 2013/04/29
- メディア: ペーパーバック
- この商品を含むブログを見る
*1:こういうのを中国剰余定理というのでした。