類体論入門 - tsujimotterのノートブック

日曜数学 Advent Calendar 2020 の1日目の記事です。

「類体論」という名前を聞いたことがあるでしょうか？

類体論は、高木貞治という日本の数学者が提唱した理論です。実は今年2020年は類体論が提唱されてからちょうど 100周年だそうです。

『類体論における主要な定理の一つ「高木の存在定理」が発表されたのが1920年の国際数学者会議なのだそうです。』

と書いていたのですが、同1920年には類体論に関してまとめた論文を、東京大学の理学部紀要にて発表しているそうです。（せきゅーんさんよりご指摘いただきました。）

後者の論文から100周年というのがより適切かもしれません。

整数論に興味がある方は、名前を聞いたことあるかもしれません。一方で、その主張について知っている人はあまり多くないのではと思います。かくいう私も、これまで類体論について勉強を続けてきましたが、いつまでたっても全容がわからず苦労しました。最近ようやく、（あくまで個人的な実感として）その雰囲気がわかってきたような気がしています。難しいけれど、理解しようと思える価値がある理論だと思っています。

類体論を勉強しようと思い専門書や他の方の記事を読んでみたときに、解説の難易度は大きく二極化しているように思います。類体論的な現象を説明するに留まって類体論そのものについては十分解説されないものと、正確な主張が述べられてはいるが難解なもの。後者については、じっくり読むことで内容は理解できるかもしれませんが、抽象的すぎて前者の記事との繋がりがなかなか見えてこなかったりします。

今回の記事では、その間を繋ぐものを目指したいと思います。わかりやすい類体論的現象からスタートして、類体論の主張まで到達したいと思います。難解になりすぎず、類体論の全体像を雰囲気だけでも伝えるような「類体論の入門記事」を書いてみたいと思います。

もちろん、優しい記事を目指すといっても、前提知識は必要になります。群・環・体の基本的な事項や特にガロア理論は前提となってしまいます。難しい部分にはできるだけ踏み込まないように説明しますので、その辺の知識に自身がないという方も、よろしければ分からないところは飛ばしつつ読んでいただければと思います。

目次は以下の通りです。少し長い記事になりますが、ぜひ最後までお付き合いください！

目次：

1. フェルマーの2平方定理

2. 数の世界を広げる

3. 円分体のガロア群と分解法則

4. 円分体でない場合の分解法則

5. 類体とは何か

6. 類体論とは

7. おわりに

関連書籍

関連するtsujimotterのノートブックの記事

他の方の解説

1. フェルマーの2平方定理

類体論の源流は、今から300年以上昔のフェルマーに遡ります。（類体論からさらに200年以上昔です。）

奇数の素数 $p$ に対して、 $p$ が整数 $x, y$ を用いて

$p = x^2 + y^2$

と表される必要十分条件は、 $p$ が $4$ で割って $1$ あまることである。

この定理はフェルマーによって発見され、オイラーによって証明されました。素数が2つの平方数で表されるための必要十分条件を与えているので、フェルマーの2平方定理と呼ばれます。

実際、 $p = 5, 13, 17, 29$ のときは

$5 = 1^2 + 2^2$

$13 = 2^2 + 3^2$

$17 = 1^2 + 4^2$

$29 = 2^2 + 5^2$

のようにそれぞれ2つの平方数の和で表せます。一方、 $7, 11, 19, 23$ のような数は2つの平方数の和では表すことができません。

ここで不思議に感じていただきたいのは、「 $p$ が2つの平方数の和で表せること」と「 $p \equiv 1 \pmod{4}$ 」が関係するということです。

もちろん、 $x, y$ の偶奇を考えることで、 $p \equiv 3 \pmod{4}$ である素数が2つの平方数の和では表せないことは直ちに分かります。しかしながら、 $p \equiv 1 \pmod{4}$ である素数が2つの平方数の和で表せる理由は何なのでしょう。直感的にはその理屈は明らかではありません。*1

類体論は「フェルマーの2平方定理の必要十分条件が $\bmod{4}$ で表されること」の真の意味を理解し、徹底的に一般化していくための試みと考えられます。

フェルマーの2平方定理についての初等的な解説はこちら：
tsujimotter.hatenablog.com
tsujimotter.hatenablog.com

2. 数の世界を広げる

フェルマーの2平方定理の問題を言い換えていきましょう。

$p = x^2 + y^2$ という式に対して、虚数単位 $i = \sqrt{-1}$ を加えて無理やり因数分解してしまいましょう。

$p = x^2 + y^2 = (x+iy)(x-iy)$

最右辺は、 $(整数)+i(整数)$ という形の積になっています。

素数 $p$ は整数の世界においてはこれ以上分解することができませんが、 $(整数)+i(整数)$ という形の数の世界まで世界を広げてあげれば、分解されてしまうこともあるというわけですね。このような $(整数)+i(整数)$ という数全体の集合を $\newcommand{\zz}{\mathbb{Z}}\zz[i]$ と表すことにします。

$\mathbb{Z}[i]$ を使うと、次のように問題を言い換えることができます。

奇数の素数 $p$ が $\zz[i]$ において分解するための必要十分条件は、 $p \equiv 1 \pmod{4}$ が成り立つことである。

相変わらず $\bmod{4}$ である理由はよく分かりませんが、問題の見え方はずいぶん変わったと思います。問題は「数の世界を広げたときに、素数がどのように分解するか」にあったということですね。我々が知りたかったのは、素数の分解法則であったというわけです。

分解の様子を図に表すとこうなります。

しばしば「素数 $p$ を $\zz[i]$ に持ち上げる」というような表現を用いるので、 $\zz[i]$ を図の上側に $\zz$ を図の下側に表しています。

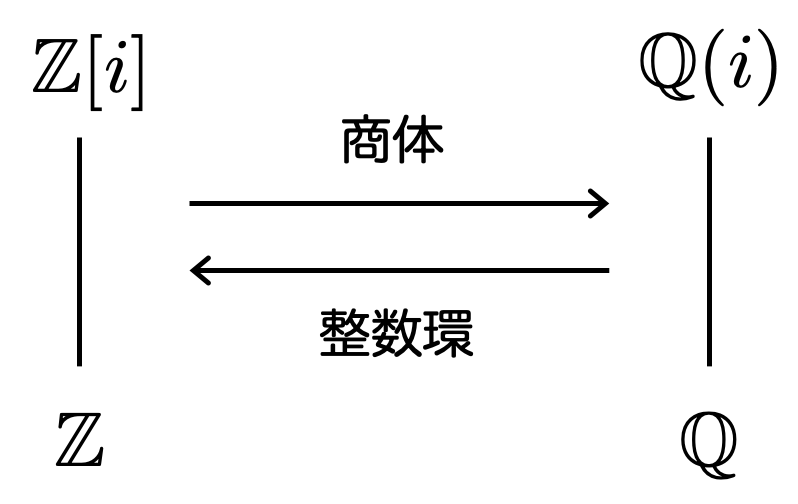
ところで分解法則を考えるにあたっては、 $\zz$ や $\zz[i]$ のような「環の拡大」を考えるよりは、「体の拡大」を考える方が一般的です。

$\zz$ の商体をとると有理数体 $\newcommand{\qq}{\mathbb{Q}}\qq$ に、 $\zz[i]$ の商体をとると $\qq(i)$ が得られますが、これらの体の間の拡大 $\qq(i)/\qq$ を考えるのです。

逆に、 $\qq$ の中で「整」であるような元全体を考えると $\zz$ になります。これを「整数環」といいます。 $\qq(i)$ の整数環は $\zz[i]$ です。

「 $p$ が $\zz[i]$ で分解する」を、体の言葉で「 $p$ が $\qq(i)$ で分解する」と言うことがあります。誤解を招きそうな表現ではありますが、この表現を受け入れることで「 $p$ が体 $\qq(i)$ の整数環で分解する」のような冗長な表現を避けることができます。

3. 円分体のガロア群と分解法則

体の言葉を使うと、 $\qq(i)/\qq$ は $\qq$ 上の有限次ガロア拡大ということになります。

ガロア拡大なので、ガロア群を考えることができます。体の拡大 $\qq(i)/\qq$ のガロア群には

$\newcommand{\gal}{\operatorname{Gal}}\gal(\qq(i)/\qq) \simeq (\zz/4\zz)^\times$

という同型があります。ここで、 $(\zz/4\zz)^\times$ は $\bmod{4}$ の既約剰余類群で

$(\zz/4\zz)^\times = \{ 1, \; 3 \pmod{4} \}$

なる元の集まりです（1, 3は4と互いに素な4未満の整数）。ガロア群を考えることで「 $\bmod{4}$ 」との関係性が見えてきました。

一般に、 $\zeta_n$ を1の原始 $n$ 乗根としたとき、 $\qq$ に $\zeta_n$ を添加した体を $\qq(\zeta_n)$ を書いて $n$ 次円分体といいます。上の $\qq(i)$ は、1の原始4乗根を添加しているので、4次円分体ですね。

この円分体のガロア群には

$\gal(\qq(\zeta_n)/\qq) \simeq (\zz/n\zz)^\times$

なる同型が存在します。右辺は $\bmod{n}$ の既約剰余類群です（nと互いに素なn未満の正整数全体が乗法についてなす群）。

これに関連して次のような必要十分条件が得られます。

$n$ を割り切らない素数 $p$ に対して、次が成り立つ：

$p \equiv 1 \pmod{n}$ $\Longleftrightarrow$ $p$ が $\qq(\zeta_n)$ で完全分解する

「完全分解する」という用語が未定義でしたが、 $p$ が $[\qq(\zeta_n) : \qq]$ 個の「素数」の積に分解されるという意味です。分解される素数の個数は拡大次数以下である、という一般論があります。拡大次数いっぱいの分解を完全分解と呼ぶわけですね。

ここでは単に「素数」と書いていますが、実際は $\qq(\zeta_n)$ の「素数」ではなく、「素イデアル」を考えることになりますが、今回は難しいのでやめておきましょう。

「イデアル」や「素イデアル」について詳しく知りたい方は、こちらの記事が参考になります：
tsujimotter.hatenablog.com

いわば「円分体の分解法則」といえるこの法則の背景を、少しだけ説明しておきたいと思います。この背景にはフロベニウスという重要な対象があります。

フロベニウスとは、（ここで正確な定義は述べませんが）素数 $p$ に対して定まる $\gal(\qq(\zeta_n)/\qq)$ の元 $\sigma_p$ のことです。

これが $p$ の $\qq(\zeta_n)$ における分解法則を司っています。実際、 $p$ が $\qq(\zeta_n)$ で完全分解することの必要十分条件は、 $\sigma_p$ が $\gal(\qq(\zeta_n)/\qq)$ において単位元であることです。

さらに、先ほどのガロア群の同型 $\gal(\qq(\zeta_n)/\qq) \simeq (\zz/n\zz)^\times$ に対して、その同型写像はフロベニウスの対応（ $\sigma_p$ が $p\pmod{n}$ に対応する）によって与えられるという事実があります：

$\begin{align*} \gal(\qq(\zeta_n)/\qq) &\xrightarrow{\;\sim\;} (\zz/n\zz)^\times, \\ \sigma_p &\longmapsto p \pmod{n} \end{align*}$

これは相互法則と呼ばれます。この対応関係が群の同型写像を与えるというのがポイントで、実際

単位元 $\; \longmapsto \; 1\pmod{n}$

という対応関係により、次のことがわかるわけです：

$p$ が $\qq(\zeta_n)$ で完全分解する
$\Longleftrightarrow$ $\sigma_p$ が $\gal(\qq(\zeta_n)/\qq)$ において単位元
$\Longleftrightarrow$ $p \equiv 1 \pmod{n}$

フェルマーの2平方定理は、円分体の分解法則の特殊ケースとして（ $n = 4$ のとき）成り立つのだということですね。

この節で述べたフロベニウスについては、より詳しい解説があります：
tsujimotter.hatenablog.com

4. 円分体でない場合の分解法則

フェルマーの2平方定理が円分体の分解法則として理解できたので、「めでたしめでたし」としたいところですが、もう少しだけ話を進めてみましょう。だんだんと類体論に近づいていっています。

フェルマーの2平方定理は $\qq(i)$ における分解法則に関係していて、 $\qq(i)$ は「たまたま」4次の円分体なのでした。円分体とは限らない場合の分解法則は、どのように考えたら良いのでしょうか。

たとえば、 $\qq(\sqrt{-7})$ は $\qq$ 上の2次拡大ですが、円分体ではありません。この場合の分解法則はどのように考えたら良いでしょうか。実は、ここでも円分体の考え方が使えるのです。

$\qq(\sqrt{-7})$ は円分体 $\qq(\zeta_7)$ に包含される（ $\qq(\sqrt{-7}) \subset \qq(\zeta_7)$ が成り立つ）というのがポイントです。実際、 $\sqrt{-7}$ は

$\sqrt{-7} = (\zeta_7 + \zeta_7^2 + \zeta_7^4) - (\zeta_7^3 + \zeta_7^5 + \zeta_7^6)$

と表せるので、 $\qq(\sqrt{-7})$ の任意の元は、 $\qq(\zeta_7)$ によって表せるというわけですね。

$\sqrt{-7} = (\zeta_7 + \zeta_7^2 + \zeta_7^4) - (\zeta_7^3 + \zeta_7^5 + \zeta_7^6)$ という式には「ガウス和」が関係します：
tsujimotter.hatenablog.com

この包含関係を元に、体の拡大とガロア群の対応関係を次のように表します。

$\qq(\sqrt{-7})$ を固定するガロア群 $\gal(\qq(\zeta_7)/\qq(\sqrt{-7}))$ は、 $\qq(\sqrt{-7})$ の任意の元

$a+b\sqrt{-7} = a+b\{(\zeta_7 + \zeta_7^2 + \zeta_7^4) - (\zeta_7^3 + \zeta_7^5 + \zeta_7^6)\}$ （ $a, b \in \qq$ ）

を固定する元全体ということなので、 $\sigma_i \colon \zeta_7 \mapsto \zeta_7^i$ として

$\gal(\qq(\zeta_7)/\qq(\sqrt{-7})) = \{ \sigma_1, \; \sigma_2, \; \sigma_4 \}$

ということになります。これに対応する $(\zz/7\zz)^\times$ の部分群は

$H = \{ 1, \; 2, \; 4 \pmod{7} \}$

ということになりますね。

ここで分解法則は、次のように表せます。

$p$ が $\qq(\sqrt{-7})$ で完全分解する
$\Longleftrightarrow$ $\sigma_p$ が $\gal(\qq(\sqrt{-7})/\qq)$ において単位元
$\Longleftrightarrow$ $p$ が $(\zz/7\zz)^\times / H$ において単位元
$\Longleftrightarrow$ $p \in H$

結局、円分体 $\qq(\zeta_7)$ を通して、 $\qq(\sqrt{-7})$ の分解法則が $\bmod{7}$ で表せたことになります。このことから、次のようなわかりやすい法則も得られます。

7ではない任意の素数 $p$ に対して、 $p$ が整数 $x, y$ を用いて

$p = x^2 + 7y^2$

と表される必要十分条件は、 $p \equiv 1, 2, 4 \pmod{7}$ であることである。

一般に、 $K$ を $\qq$ 上の有限次アーベル拡大体とします。アーベル拡大とは、ガロア拡大かつガロア群がアーベル群（任意の元が可換）であるような拡大のことです。

このとき、ある正の整数 $N$ が存在して、 $K \subset \qq(\zeta_N)$ が成り立ちます。これをクロネッカー・ウェーバーの定理と言います。言い換えると、 $\qq$ 上のアーベル拡大は必ず円分体に包含されるということですね。「 $\qq$ 上の」というところがポイントで、 $\qq$ 上でない場合は一般には成り立ちません。

そのため、任意の $\qq$ 上のアーベル拡大に対して、 $\qq(\sqrt{-7})$ のときと同様、円分体を通して分解法則がわかるというわけですね。面白いですね！

5. 類体とは何か

ここまでは、あるアーベル拡大があったとき、その分解法則を考えてきました。今度は、その逆を考えてみましょう。すなわち、分解法則が先に与えられたときに、対応する拡大体は存在するのかという問題です。実際、適切なセッティングの元、それは可能です。

具体的に、 $(\zz/n\zz)^\times$ の任意の部分群 $H$ に対して

$p \in H$ $\Longleftrightarrow$ $p$ は $K/\qq$ で完全分解する

を満たすようなアーベル拡大 $K/\qq$ が存在したとします。このような $K$ を $H$ の類体と呼ぶことにしましょう。

$(\zz/n\zz)^\times$ やその部分群 $H$ は $\zz$ の元を $\bmod{n}$ で「類別」しているわけですが、その類別に対応する体なので「類体」というのだと思います。

このような「類体が存在するか」というのが類体論の主テーマです。だから類体論というわけです。

実際、 $H$ の類体 $K$ は必ず存在します。そして、このときガロア群の同型

$\gal(K/\qq) \simeq (\zz/n\zz)^\times \big/ H$

が成り立ちます。

体の拡大・ガロア群・分解法則の三本柱が一体となっているわけですね。

$K/\qq$ のガロア群の構造は、既約剰余類群 $(\zz/n\zz)^\times$ の剰余群となりますので、類体はアーベル拡大であるというのもポイントです。

一つ具体例を考えてみましょう。たとえば $(\zz/20\zz)^\times$ の部分群として

$\{1 \pmod{20}\}, \;\; \{1, 9 \pmod{20}\}, \;\; \{1, 3, 7, 9 \pmod{20}\}, \;\; (\zz/20\zz)^\times$

がありますが（他にも4つ部分群がありますが省略）、これらに対応する類体は次のようになります：

いずれの行も、右側の部分群に含まれる素数だけが、左側の体で完全分解することになります。

6. 類体論とは

いよいよ類体論までやってきました。これまでは $\qq$ 上の拡大について考えてきましたが、高木貞治の提唱した類体論は、一般の代数体 $K$ 上の拡大についての理論です。今まで $\qq$ と書いていたところが全部 $K$ になるわけですね。

よって、素数 $p$ の分解法則も、 $K$ における「素数」に置きかわります。 $K$ の「素数」が、さらに上の体において分解するかどうか考えたいわけですね。実際は、 $K$ の「素数」そのものではなく、 $K$ の（整数環の）「素イデアル」を考えることになります。

$\qq$ 上のときのように、 $K$ の素イデアルが $K$ より大きな体 $L$ の中で分解される法則を、わかりやすく理解することができるでしょうか？

実際、 $L/K$ がアーベル拡大ならばそれができるというのが、類体論の主要な主張です。「主要な」と書きましたが、類体論は「理論」なので一つの定理というわけではありません。以下に説明するようないくつかの定理の集合体となっています。

まずは、類体論の主役とも言える類体について定義しましょう。円分体のときと同じように定義します。円分体のときは、 $(\mathbb{Z}/n\mathbb{Z})^\times$ の部分群 $H$ に対して、 $H$ の素数が完全分解するような $\qq$ 上の拡大を考えました。

$\bmod{n}$ の既約剰余類群 $(\mathbb{Z}/n\mathbb{Z})^\times$ に対応する群として

「 $\bmod{\mathfrak{m}}$ の合同イデアル類群」

という群を考えます。 $\mathfrak{m}$ は整イデアルです。「 $\bmod{\mathfrak{m}}$ の合同イデアル類群」の定義は詳しく説明しませんが、 $K$ のイデアル全体を $\bmod{\mathfrak{m}}$ で「類別」しているのだと思っていただければと思います。

$(\mathbb{Z}/n\mathbb{Z})^\times$ の場合は、整数全体を単に $\bmod{n}$ で割った余りで分類しただけでした。

「 $\bmod{\mathfrak{m}}$ の合同イデアル類群」では、イデアル全体をまず単項イデアルで割った剰余類を考えて、さらに $\bmod{\mathfrak{m}}$ で分類するような構造になっています。より細かい分類をしてるイメージですね。

さて、この「 $\bmod{\mathfrak{m}}$ の合同イデアル類群」の部分群として $H(\mathfrak{m})$ を考えます。この $H(\mathfrak{m})$ によって分解法則が与えられるような $L/K$ が $H(\mathfrak{m})$ の類体の定義です。

すなわち、 $K$ の任意の「素数」（実際は「素イデアル」） $\mathfrak{p}$ に対して、正確にいうと「 $\mathfrak{p}$ は $\mathfrak{m}$ で割り切れない」ものに限りますが

$\mathfrak{p} \in H(\mathfrak{m})$ $\Longleftrightarrow$ $\mathfrak{p}$ が $L/K$ で完全分解する

が成り立つような、 $K$ 上の拡大体 $L$ を $H(\mathfrak{m})$ の類体といいます。

さて、このような類体は必ず存在し、しかもただ一つ存在します。これこそが、冒頭で述べた類体論の主要な主張である存在定理です。

つまり「 $\bmod{\mathfrak{m}}$ の合同イデアル類群」の部分群を考えると、それが分解法則にちょうど一致するような体（すなわち類体）が必ず存在するというわけです！面白いですよね！

ここで、どんな $K$ 上の拡大体が類体になっているかが気になると思います。実は、 $L/K$ が有限次アーベル拡大であれば、類体になっているというのです。これは基本定理と呼ばれる定理の主張です。したがって、任意の有限次アーベル拡大に対して、分解法則が $\bmod{\mathfrak{m}}$ で定まることが言えるわけですね。

ガロア群の対応関係もみてみましょう。

基本定理により $L/K$ がアーベル拡大のとき、具体的に $L/K$ に対応するような $\mathfrak{m}$ と「 $\bmod{\mathfrak{m}}$ の合同イデアル類群」の部分群 $H_{L/K}(\mathfrak{m})$ を考えることができます。

このとき、 $L/K$ のガロア群の同型も具体的に得られます：

$\gal(L/K) \simeq$ 「 $\bmod{\mathfrak{m}}$ の合同イデアル類群」 $\big/ H_{L/K}(\mathfrak{m})$

また、「 $\bmod{\mathfrak{m}}$ の合同イデアル類群」の部分群として単位群を考えると、 $\bmod{\mathfrak{m}}$ の最大の類体が得られます。これを $K$ 上の $\bmod{\mathfrak{m}}$ のray類体といって、 $K(\mathfrak{m})$ と表すことにします（ $K(\mathfrak{m})$ は $K$ に $\mathfrak{m}$ の元を添加するという記号ではありません）。

すると、 $K(\mathfrak{m})/K$ のガロア群は、合同イデアル類群にちょうど一致します：

$\gal(K(\mathfrak{m})/K) \simeq$ 「 $\bmod{\mathfrak{m}}$ の合同イデアル類群」

ray類体はちょうど $\qq$ のときの円分体に対応する体ですね。 $K(\mathfrak{m})$ を用いて、ガロア群の対応関係を描くと、円分体のときと同じような図を描くことができます：

体の拡大・ガロア群・分解法則は、すべて綺麗に一対一に対応していたというわけです。美しすぎますね。これを美しいといわずに、何を美しいといえばよいでしょうか。

最後に「フェルマーの2平方定理の必要十分条件が $\bmod{4}$ で表されること」について、類体論を用いた説明を考えてみましょう。

$K = \qq$ とします。 $\mathfrak{m} = (4)\infty$ （ $\infty$ は無限素点）とすれば「 $\bmod{\mathfrak{m}}$ の合同イデアル類群」は $(\mathbb{Z}/4\mathbb{Z})^\times$ に一致します。

$(\mathbb{Z}/4\mathbb{Z})^\times$ の部分群として $\{ 1 \pmod{4} \}$ がありますが、存在定理によりこれに対応する類体がただ一つ存在します。実際、 $L = \qq(i)$ が対応する類体になります。

したがって類体の定義から、 $p \equiv 1 \pmod{4}$ であるような素数だけが $L$ で分解するということになり、フェルマーの2平方定理が得られます。思えば遠くまで来たものですね。

7. おわりに

最後に、ここまでの話をまとめたいと思います。

まず、私たちの関心は、フェルマーの2平方定理がなぜ $\bmod{4}$ で表されるのかということでした。この問題を深く深く追いかけて、任意のアーベル拡大に対して分解法則が $\bmod{\mathfrak{m}}$ で定まるという類体論に行き当たるのでした。

このようなアーベル拡大は類体と呼ばれますが、類体はアーベル拡大に限られるということも類体論は主張しています。

こんなに美しい理論が100年前にできていたというのがすごいですね。アーベル拡大のことが、少なくとも分解法則に関して言えばほとんど理解し尽くされたといってよいわけですね。これはすごく面白いことだと思います。

しかもそれを作ったのが日本人というのは、ありきたりな言葉かもしれませんが同じ日本人として嬉しいです。

アーベル拡大は類体論によってわかったということで、次は非可換の場合はどうなのかと思うかもしれません。これについては、非可換類体論と呼ばれるジャンルがあるそうで、完全には解決していないかと思いますが、色々と進展があるようです。私にはまったく解説する力はありませんが。

そんなわけで、類体論100周年にかこつけて、類体論を解説する記事を書いてみました。私自身、2014年ごろに加藤和也先生の「数論への招待」を読んで、それをきっかけに類体論に興味を持ち始めました。これまでも色々な形で、類体論については触れてきましたが、6年ほどかかりましたがようやく自分なりに納得する解説を書くことができたと思います。

もちろん、まだまだ説明不足なところはたくさんあって、触れていない部分（分岐の話、素イデアルの話などなど）や、私が理解していない部分も多々あります。この記事を読んで、類体論に興味を持っていただけましたら、ぜひ関連する書籍にも手を伸ばしていただければと思います。

それでは、今日はこの辺で！

最後になりましたが、今回の記事は「日曜数学アドベントカレンダー2020」の第１日目の記事となります。続く記事もお楽しみに！
adventar.org