日曜数学 Advent Calendar 2019 の1日目の記事です。
アドベントカレンダーの季節がやってまいりました。今年も日曜数学アドベントカレンダーを立てまして、この記事はその1日目の記事となっています。
adventar.org
実は、日曜数学アドベントカレンダーは、今年で 5年目 になります。なかなか続いていますね。
今年も既に22件が埋まっていまして、たくさんの方が思い思いの数学について熱く語ってくださいます。とても楽しみです。
トップバッターのこの記事は 超幾何関数 をテーマにお話したいと思います。
もともとこのtsujimotterのノートブックは、私の日曜数学の成果を発表する場として書いていて、今勉強している最前線をその熱が冷めないうちに書くのが特徴です。その意味で、今回の話は私がまさに今勉強中の内容であり、tsujimotterのノートブックらしい記事かと思っています。
ちょっと難しい内容になるかと思いますが(そしていつも通りとても文章が長いのですが)、よろしければお付き合いいただけますと幸いです。
1. 超幾何関数の3つの顔
オイラーやガウスによって研究された、以下の形の級数から話を始めましょう。
は複素数のパラメータで適切な値を取ることにし、
は複素数の変数とします。
はポッホハマー記号と呼ばれるもので、定義は
です。
式 の級数の収束半径は
であることが(少し考えると)わかるので、
は複素数平面上の単位円の内側で定義される1変数関数となります。これを超幾何級数というのでした。
tsujimotter.hatenablog.com
そろそろ「こいつ」とも仲良くなりたいと思って、勉強を進めているところです。
ところで「超幾何関数がテーマ」と言っておきながら、式 のことを「超幾何級数」と呼んでいることに違和感を覚えた人もいるのではないでしょうか。これには意図があって、あえて使い分けています。
あとで議論しますが、式 の級数の定義域は
ですが、実は
を除く複素数平面全体に解析接続することができます。この解析接続された関数を超幾何関数と呼ぶことにしたいのです。
式 そのものは、あくまで超幾何関数という関数の級数表示ということですね。級数表示が超幾何関数の第1の顔です。これは超幾何関数を表す一つの形であって、これがすべてではありません。
解析接続というキーワードが登場しましたが、超幾何関数の解析接続を考えるにあたって重要になるのは、超幾何関数の満たす微分方程式です。上の級数を とおくと、
は次の微分方程式を満たします:
式 は(ガウスの)超幾何微分方程式と呼ばれ、超幾何関数の第2の姿です。
超幾何関数の第3の顔は積分表示です。 が適当なパラメータのときに、超幾何関数は次のような積分によって表すことができます。
積分表示は次の記事で導いているので、興味がある方は読んでみてください。
tsujimotter.hatenablog.com
ここまで超幾何関数の3つの顔について説明しましたが、今回の主役は積分表示です。記事の目的は、この積分表示を「接続問題」と呼ばれる問題に応用する方法です。接続問題についてはあとで具体的に述べますが、簡単にいってしまえば「微分方程式で表される解が、どのように解析接続されるのか」という問題です。
当然、微分方程式についての知識が必要になりますので、まずはじめに微分方程式に関する基本的な話をしたいと思います。それに付随して多価関数という概念が必要になりますので、そのあたりも説明したいと思います。
その後、接続問題について述べて、最後に積分表示を使って接続問題を解く方法について述べたいと思います。
目次:
2. 超幾何微分方程式とその局所解
ガウスの超幾何微分方程式(式 )の両辺を
で割ると
が得られます。この微分方程式は、最高次の係数が であり、係数が有理関数となっていて、
について線形な方程式になっています。このような方程式は、一般に線形微分方程式と呼ばれ、特に階数が2となっています。
お恥ずかしながら、tsujimotterはこれまで定係数のものしか扱ったことがなく、最近になって初めて係数が関数であるような微分方程式を勉強しました。超幾何微分方程式のようなものも線形微分方程式の範疇に入るのかと驚きました。
線形微分方程式の著しい性質として「係数の関数の振る舞いを観察することで、解の大域的な解析接続の様子がわかる」というものがあります。
具体的には、係数の関数は
であり、これらは を除く点で正則な関数となっています。したがって、
とすると、上の2つの関数は
上正則ということになります。
このとき、微分方程式 の解は、
内にくまなく解析接続されることが、線形微分方程式の一般論から帰結されます。
という特異点の情報しか見ていないのに、大域的な振る舞いがわかってしまうのは面白いと思います。
さらに、 を
内の単連結な部分領域としたとき、微分方程式の階数を
とすると、
上の解全体は
上の
次元ベクトル空間をなします。今回は
なので、2次元の
ベクトル空間となります。
単連結を強調したのは、上の は単連結ではないからです。単連結とは要するに穴が空いていない領域のことで、
には
に穴が空いているので単連結ではありません。
したがって、式 のような微分方程式においては、大域的に解の空間を考えられるわけではなく、あくまで局所的な領域で解の空間を考えることになります。そこで、局所的な領域において、解の空間がどのようなものになっているかについて興味が出てきますね。
関数の多価性
ただ、ここで少しやっかいな問題が生じます。関数の多価性です。
多価性について、有名な多価関数 を使ってイメージを説明したいと思います。
というのは、
で複数の値をとります。複数の値をとるのは、周期関数である指数関数
の逆関数として
が定義されているからです。
は
を左回りに一周して元の位置に戻ってくると
されるような関数となっていて、以下の図のような振る舞いをします。

逆に「 の周りを何回周ったか」も含めた「拡張された面」を考えることで、
上の多価関数である
を一価関数とみなすことができるようになります。このような「拡張された面」のことを普遍被覆面といい、
と表します。
「今回は超幾何級数の話だろう。 なんか考えてどうするんだ?」と思うかもしれません。ところが、一見何の変哲もないようにみえる関数が、
の影響を受けて多価関数になってしまうのです。
たとえば を複素数の定数として
のような関数もそうです。
は
のように定義されるため、 が現れます。この関数も、
の周りを左回りに1周すると
倍されます。こんなシンプルな関数でも多価関数になってしまうのですね。実際、この
倍されるという事実は、超幾何関数の多価性を考える上でも必要になりますので覚えておいてください。
別の記事でまとめたので、よかったらご覧になってください:
tsujimotter.hatenablog.com
さて、前置きが長くなりましたが、超幾何関数もやはり多価関数です。 という点を一周するたびに、値が変わってしまうのです。
解析接続する上で問題になるのは、超幾何級数を の外側に接続する際に、
の下側を通るか、上側を通るかで関数の形が変わってしまうという点です。この点を考慮に入れて議論する必要があります。

として、
の普遍被覆面
を考えると、超幾何関数
は
上の一価関数と考えることができます。
局所解
線形微分方程式の局所的な解は、微分方程式の確定特異点と呼ばれる点の周りの級数展開によって具体的に記述できます。
を中心とする半径
の円板を
、
から
を除いた領域を
として、
上正則な多価関数
を考えます。
が
の確定特異点であるとは、ある正整数
が存在して
が成り立つことをいいます。たたし、この が曲者で、ざっくりいうと
の周りを
がぐるぐる周りながら近づいていくような近づき方は除く必要があります。(多価性を考えると、たしかにこういう近づき方は問題ありそうです)
上の定義は、ある関数 の確定特異点の定義でした。微分方程式の確定特異点とは、その微分方程式のすべての解がその点を確定特異点に持つこととして定義されます。
ここで気になるのは「すべての解の確定特異点を調べられるのか」という問題です。実は、線形微分方程式に限って言えば、簡単に調べることができます。
この事実を使うと、ガウスの微分方程式 の確定特異点が
であることが簡単にわかります。たとえば、
においては、係数の関数はどちらも1位の極ですから、条件を満たしますね。
についてですが、
と変数変換して、
における極の位数を考えればよいです。(関数の舞台を
ではなく
で考えているということになりますね。)
確定特異点 が決まると、その周りで以下のような線型独立な2解を構成できます。
これらの級数は、係数の関数が正則であるような領域 上で収束します。
は定数の数列で、
となります。
を定義していませんでしたが、これらは特性指数といって以下で定義されます。
を確定特異点として、
をそれぞれ微分方程式の1次, 0次の係数とする。このとき、p(x)は高々1次、q(x)は高々2次の極を持つ。
のローラン展開の
次係数を
とし、
のローラン展開の
次係数を
とする。このとき、
に関する二次方程式
を、微分方程式の における決定方程式と呼びます。この2解
が特性指数の定義です。
例として、3つある確定特異点のうち、 の周りの局所解を決定してみましょう。まず
を計算すると
が得られますが、明らかに第2項目は正則パートですね。よって、第1項目を部分分数分解して
となりますが、同様に第2項が正則パートです。よって、 次の係数は
となります。
次に ですが
より、 次の項は 0 であるため、
となります。
よって、特性方程式は
となり、特性指数は となります。
実はこの に相当したのが、元々の超幾何関数の級数表示
だったのです。
に対応する解はそれぞれ
と計算できます。特に となっています。どちらも
で収束します。
同様に、確定特異点 から線型独立な解
が、確定特異点
から
が得られます。それぞれ、
の範囲で収束します。
各確定特異点の周りの局所解は、以下の図の領域で定義されます。
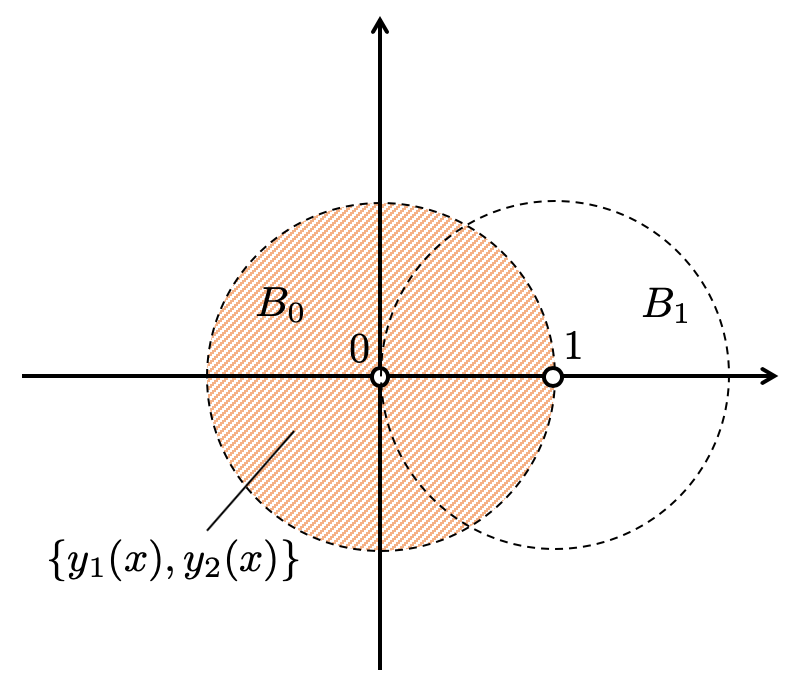
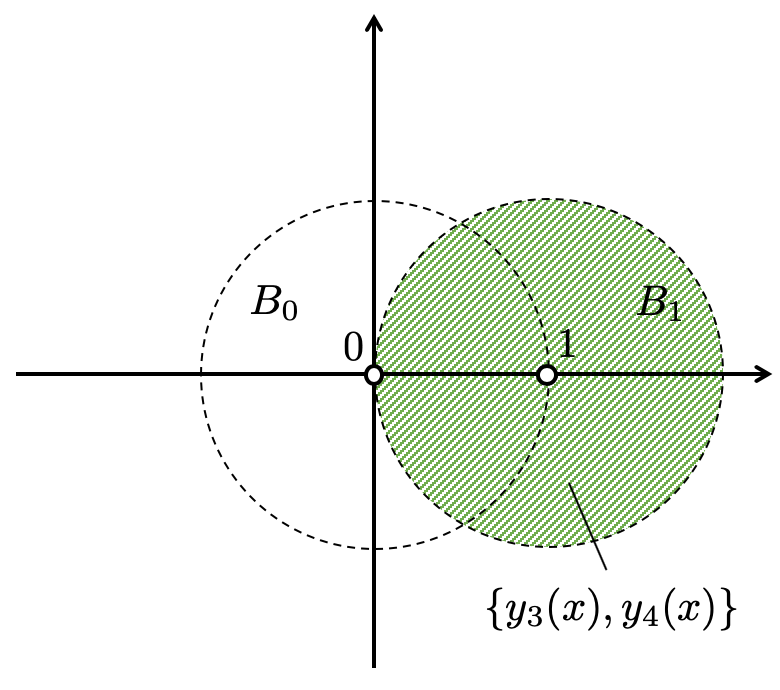
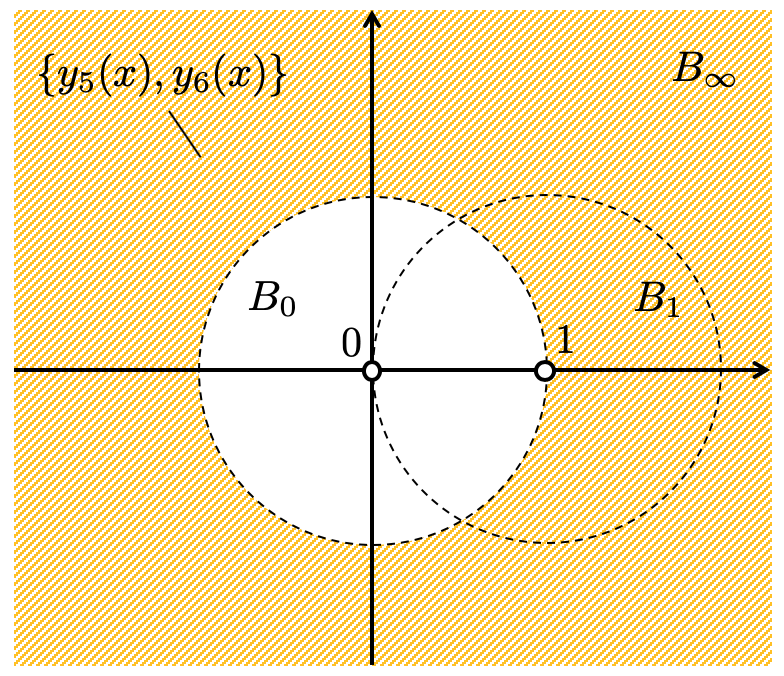
余談ですが、線形微分方程式の局所解は、確定特異点の情報と、それぞれの特性指数によって決定されることがわかります。そこで、それらを並べた表を考えたくなるわけです。これをリーマンスキームというそうです。
超幾何微分方程式のリーマンスキームは次の通りです。
一般に、特異点を確定特異点しか持たない微分方程式をフックス型の微分方程式といいます。超幾何微分方程式は、確定特異点しか持たないため、フックス型であるといえます。
今回は扱いませんが、3点を確定特異点に持つフックス型の微分方程式は、変数変換で超幾何微分方程式に帰着することが知られています。面白いですね。
3. 接続問題
さて、ここからが本題です。
のまわりの局所解がそれぞれ得られたわけですが、超幾何関数の大域的な解析接続の様子を理解するためには、それらの間を「乗り移る」ための法則を記述する必要があります。
ここでは、例として のまわりの局所解
が、
まわりの局所解
に解析接続する様子を記述しましょう。
は
上収束し、
は
上収束します。これらの定義域の共通部分である部分領域
を考えましょう。
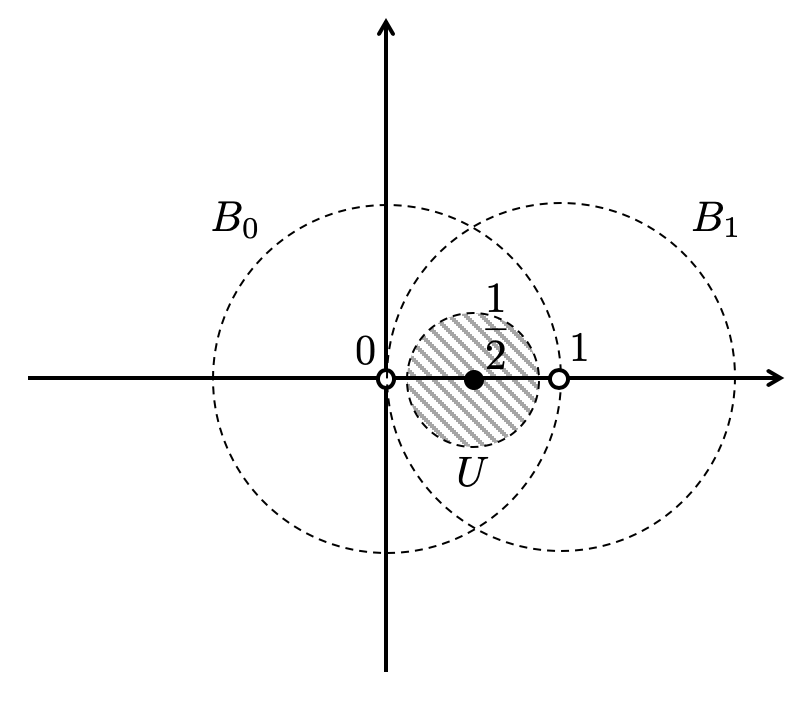
上では、
は解空間の基底の組になりますし、
も同様です。ここに、同一の2次元
ベクトル空間の異なる基底の組が得られました。したがって、基底の組の間には以下のような線形変換があるはずです。
ここで、 とします。これらの係数を接続係数と呼びます。
でしたから、上の関係式は超幾何級数
の
の外側への解析接続を与えていることになります。もう少し説明しましょう。
を含む
内の単連結な領域
を図のようにとります。

ここで、 は
上定義された正則関数になっています。また、関数
は、
において
と一致します。よって、
は本来の定義域である
の外側の領域へ拡張することができます。一致の定理より、このような拡張は
上への唯一の拡張となっています。
さらにいえば、接続係数は超幾何関数の多価性についても教えてくれます。ここでは、 を始点として、
の周りを左回りに一周する経路を
としましょう。一般に経路
に沿った関数
の解析接続を
と表すことにして、
について考えてみましょう。
は、
が
の収束域を超えてしまうため、そのままでは考えることができません。しかしながら、接続係数を使えば解決します。
上記の計算には、解析接続の線型性を用いています。
ここで、 については、
の具体的な表示と、複素指数関数の多価性(
は
を左回りに1周すると
倍される)を思い出すと
が得られます。ここからただちに
とわかります。
よって
が得られました。
先ほどは の変換を与えましたが、その逆
を与えることで、式 から
を消すことができ、結局
を得ることができます。
同様に、 に対しても
と計算することができます。
まとめると
と表すことができました。
結局、 に沿って解析接続すると、
は上記の行列
をかけたものに変化するというわけですね。この行列
は、経路
に対する回路行列といいますが、この回路行列は接続係数を用いて記述されることもわかりました。
4. 積分表示と接続問題
前節までの議論により、接続係数を求めることによって、超幾何関数の解析接続の様子が記述できることがわかりました。
あとは接続係数を求めればよいことになりますが、どうやって計算したらよいのでしょう。
実は、ここでようやく 積分表示 が使えるのです!やってみましょう!
積分表示を再掲します。
積分表示においては、ガンマ関数で書かれた係数をとってしまっても、微分方程式の解であることに変わりはありません。よって本質的なのは積分の方です。
被積分関数
は、一見たまたま現れた関数に見えますが、実は超幾何関数を本質的に規定する関数になっています。
この関数は、3個の指数関数の積で表されています。よって 上に3つの分岐点
ともう一つ
なる分岐点を持ちます。計4つの分岐点を持つことになります。
実は、積分表示における積分の端点 は、上記の4つの分岐点のうち2つを選んだものになっています。
このように考えると、積分の端点を の別の組み合わせに置き換えた積分を考えたくなります。
を相異なる分岐点
としたとき
と定義します。ここで が元々の超幾何級数の積分表示です。ただし(ここではサボりますが)分岐を適切に決めてあげる必要があります。
より、本質的な組み合わせは
通りです。以下の6通りの積分を考えましょう。
これらの積分の間には線形関係式が成り立つということが、コーシーの積分定理を使うとわかります。以下の図で表されるような閉曲線 上の積分を考えます。
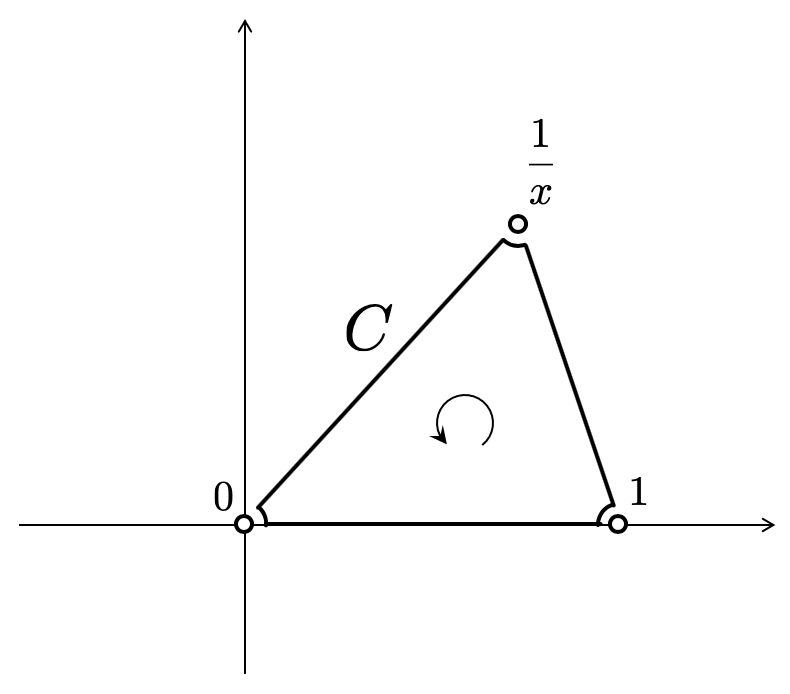
単に閉曲線を考えるだけでなく、分岐がつながるように考える必要がありますが、適切に分岐を定めるとコーシーの積分定理により
となります。
このような関係式は、 より全部で4本作れます。結局
という式が得られるわけです。
この行列のランクが4であれば(これは多くの場合成り立ちますが)、6個の のうち4個は残りの2個の線型結合で表せることになります。
もう一つ重要な事実としては、 は超幾何微分方程式
の解であるということです。力尽きてしまったので、この証明については述べられないのですが、もしこの事実を仮定すると
が微分方程式の局所解
を用いて表せることになります。
実際計算してみると、 が上に並べた順に、
の定数倍で表せることが言えます!
以上により、微分方程式の局所解の間の関係式をすべて定めることができ、結果として接続係数をすべて求めることができるのです!積分表示すごいでしょう!
5. まとめ
今回は、超幾何関数の積分表示の応用として「超幾何微分方程式の接続問題を解くための方法」を紹介しました。
個人的には、積分表示は「ガウスの超幾何定理を導くもの」程度の認識でしかなかったので、こんなにも奥深いとは思っても見ませんでした。その点が特に面白いと感じました。
線形微分方程式については、tsujimotterのノートブックで扱ったことがなかったので、基礎的なところを説明するのにずいぶんと文字数を使ってしまいました。私としても、これまで勉強したことがなかったトピックなので、今回まとめるにあたって大変勉強になりました。長い文章でしたが、最後までに読んでくださってありがとうございます。
実は、もう少し話したいことがありました。それは積分表示が「局所系係数のホモロジー・コホモロジーのペアリング」という幾何的な表現に結びついているということです。本当のことをいうと、これを説明したくて今回の記事を描き始めたのですが、ちょっと力尽きてしまいました。また機会があれば、続きを書きたいと思います。
それでは今日はこの辺で。
明日の日曜数学アドベントカレンダーは、NegeLonさんの記事です!お楽しみに!
参考文献
今回の話は、最初から最後まで原岡先生の「超幾何関数」にお世話になりました。特に今回は第0章・第1章の内容を取り扱いました。第0章の「多価関数の説明」は、個人的に感動しました。

- 作者:原岡 喜重
- 出版社/メーカー: 朝倉書店
- 発売日: 2002/10/01
- メディア: 単行本
また、今回の記事の内容に何か誤りがあれば、おそらく私の誤解から来るものかと思います。よろしければ、より正確な内容を理解したい方は上の本を読んでください。