前回書いた積分の記事が大変話題になりまして嬉しいです。
tsujimotter.hatenablog.com
今日も 積分 についての話を書いてみたいと思います。
定積分によって定義される特殊関数、ベータ関数
について紹介しましょう。
有名な特殊関数なので、ベータ関数自体は知っている方は多いかと思います。
前回の記事では、 という積分が、双曲線
上の積分だという話をしました。
実は今回の積分にも、フェルマー曲線 という曲線が背景にあります。そんな面白そうな話を紹介してみたいと思います。

目次:
1. フェルマー曲線
に対して
という式で定義される曲線 をフェルマー曲線といいます。
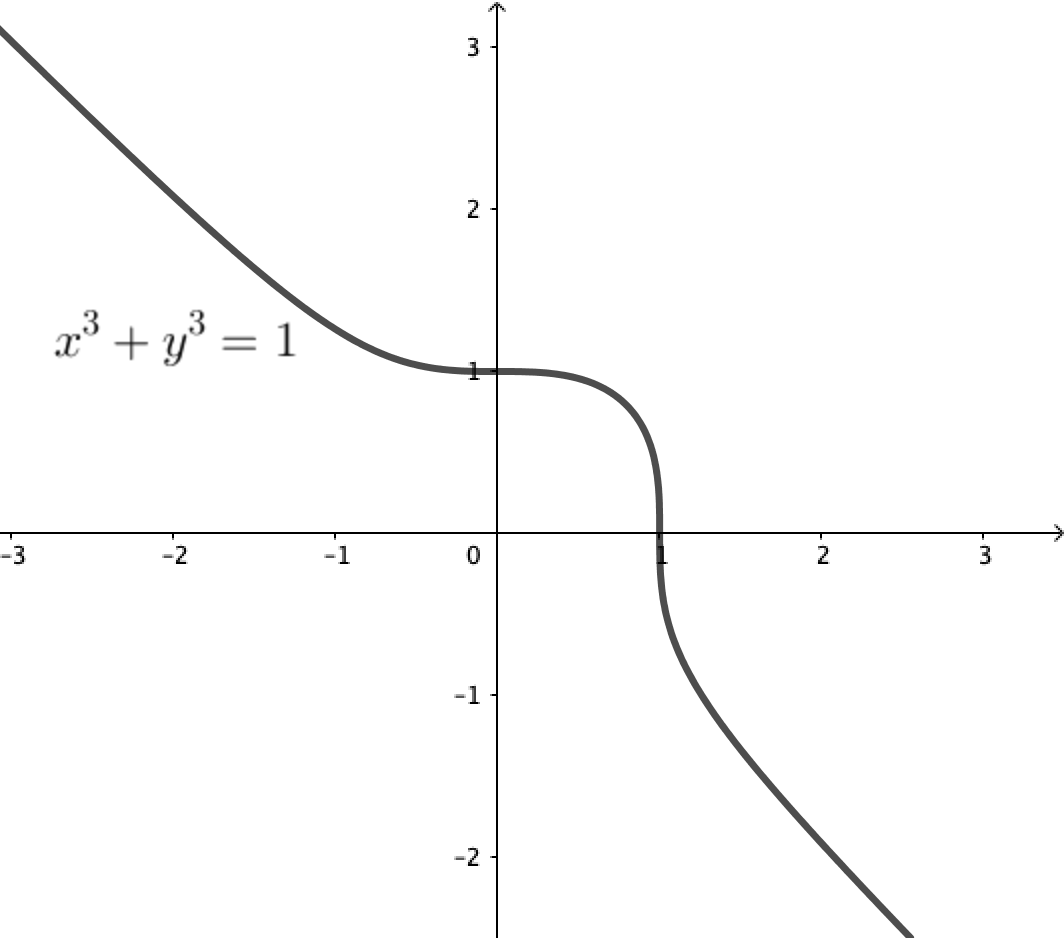

フェルマー曲線の名前の由来は、もちろん(?)あのフェルマーの最終定理(以下、FLT)です。フェルマー曲線の有理点(座標 がともに有理数である点のこと)は、FLTの方程式
の整数解に対応することが次のようにわかります:
フェルマー曲線 の有理点が存在すると仮定し、
とします。(分母は適当に通分して
に揃えておきます。)
これを に代入すると
となります。両辺 をかけると
となり、FLTの整数解が得られます。
逆に、FLTの整数解
で である組が存在すると仮定すると、両辺を
で割って
と置くことにより、
の有理点が得られます。
( の場合は、
であり、
が奇数のときは射影平面上の有理点
に対応することになりますが、これは
の無限遠点ですね。)
したがって、フェルマー曲線 の非自明な有理点の存在と、FLTの非自明な整数解の存在が同値になるわけです。FLTを「
の有理点の存在性」に言い換えることができたというわけですね。
このような経緯もあって、フェルマー曲線そのものが盛んに研究されたようですが、単にそれだけではなくフェルマー曲線自体にもさまざまな良い性質があるようです。
2. ベータ関数の変形
それでは、ベータ関数とフェルマー曲線の間にどのような関係があるのかについて、考えていきましょう。
まずは例として のケース
を計算してみます。
こんな風に変数を置き換えましょう:
なので、両辺微分して
とできます。また、
から
に対応する積分範囲は
から
ですので
ということになります。
さて、ここで式 の変数変換について考えたいと思います。
は両辺3乗すると
となります。これを
に代入して、両辺3乗すると
が得られます。これはまさに のときのフェルマー曲線
ですね!!
つまり、ベータ関数
はフェルマー曲線 上の積分だったということですね。
次に、 なる整数
に対して、有理数
におけるベータ関数
を計算したいと思います。
今度は次のように変数をおきましょう:
このとき、 であり、
です。また、
から
に対応する積分範囲は
から
です。
したがって、
となります。
そんなわけで、ベータ関数 をフェルマー曲線
上の積分
によって表すことができました。
から
の範囲で積分していますので、以下の図の「赤い線の上」で微分形式
を積分したということになりますね。
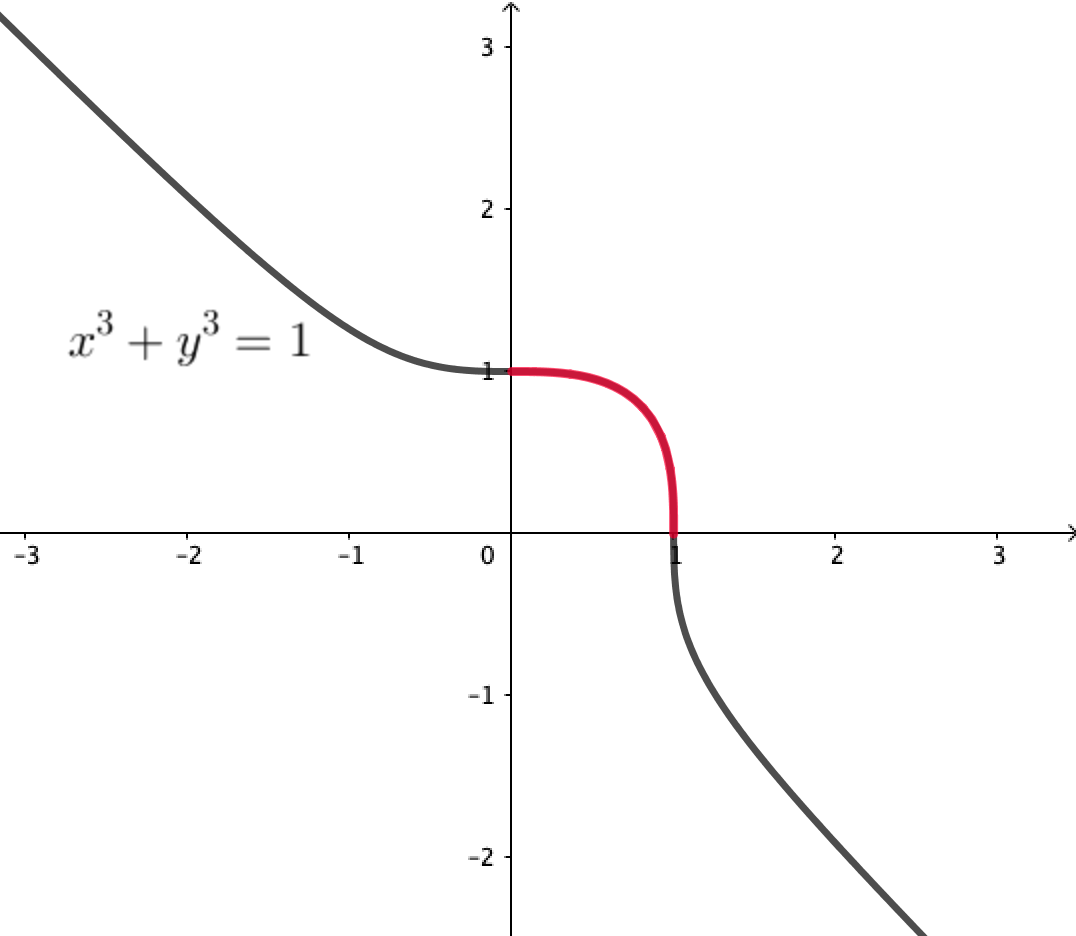
上の積分は、実は単なる積分ではなくフェルマー曲線における 周期 と呼ばれる特別な積分に関係しています。
上で述べたのは、フェルマー曲線上の微分形式 を、フェルマー曲線の一部分(
から
の範囲)で積分するとベータ関数
が得られるという話でした。
ここで、 から
を超えた範囲で積分することを考えます。思い切り範囲を大きくして、フェルマー曲線の実数点全体
で積分したものを考えてみましょう。
正確な定義はあとで述べますが、これが 周期 と呼ばれる積分です。
この「周期」という名前の由来が少しわかりづらいかもしれません。たとえば、円周の長さ の積分表示
を考えると納得できるかもしれません。この の部分は、単位円
の第一象限(図の赤い線の部分)
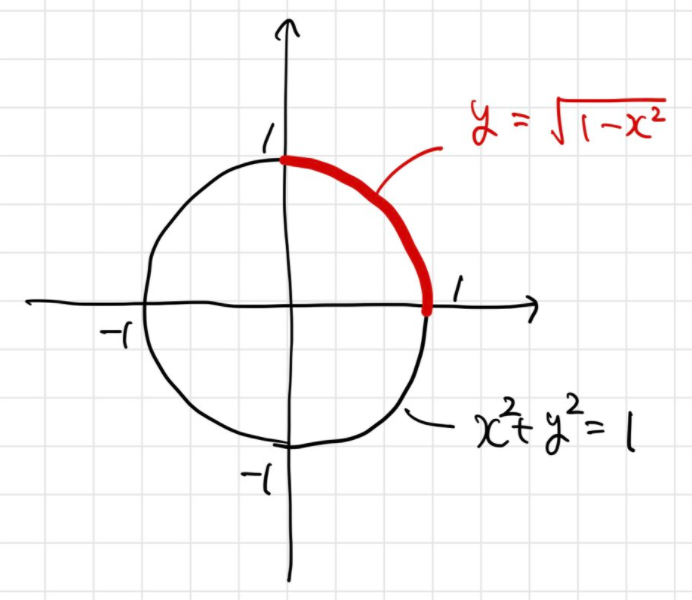
の長さを表します。したがって、4倍すれば円周全体の長さを与えることになります。
これは別の視点で見ると、「円周上で定義される微分形式」を「単位円全体」で積分した値と言えます。これが単位円上で定義される関数、すなわち三角関数の「周期」となっているわけです。
円周率はもともと「単位円の周の長さ(の半分)」として定義されますが、上記のように「単位円上の(正則)微分形式の積分」と思うこともできて、周期はその一般化と思えるわけですね。
フェルマー曲線上の積分 についても、図のように無限遠点を考慮して「フェルマー曲線の1週分」について積分していると思うと、円周率のアナロジーであると思えます。
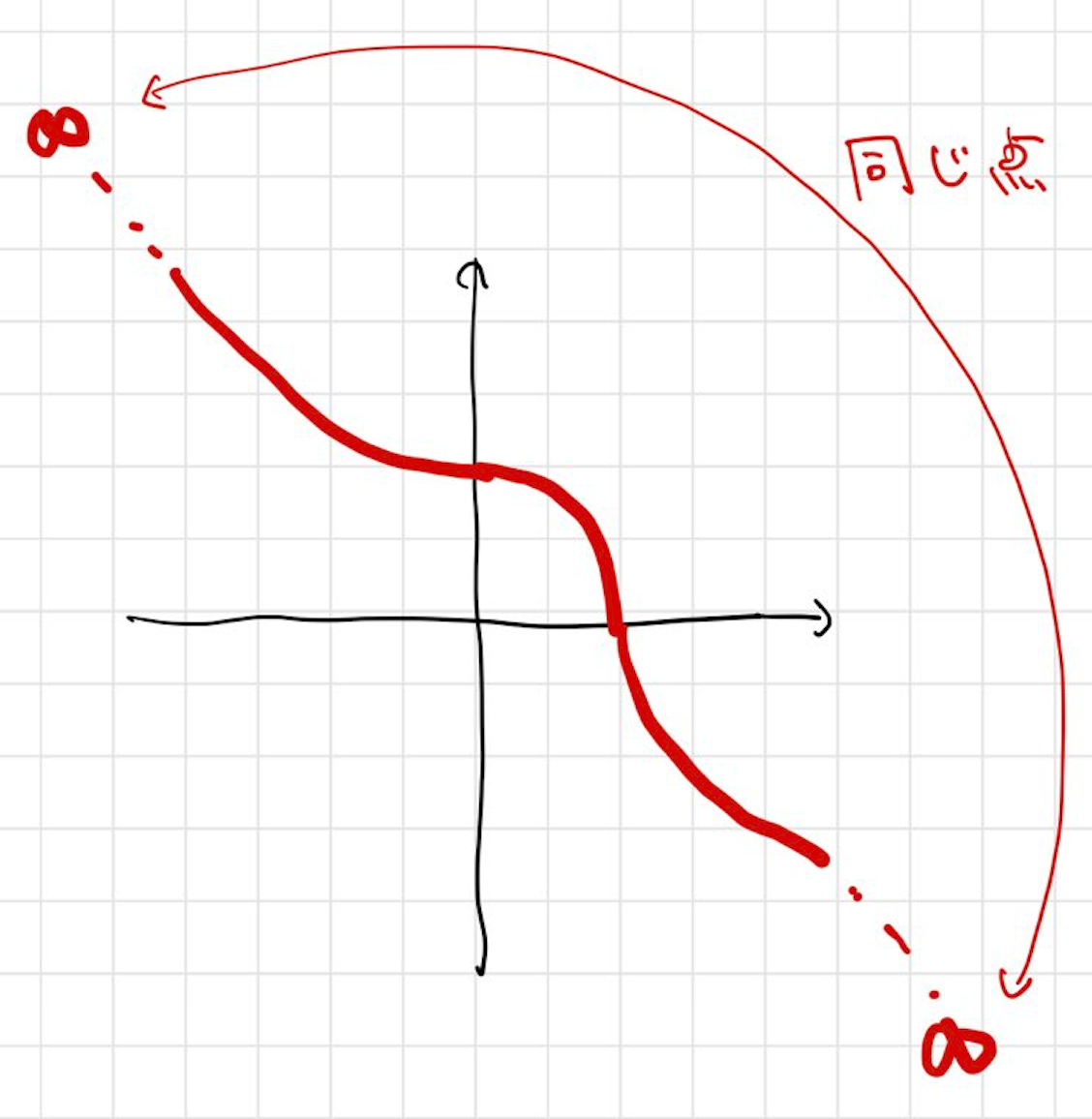
今回の記事では、リーマン面を導入して「周期」をもう少し正確に定義した上で、Rohrlichによる「フェルマー曲線上の周期を計算する公式」について紹介したいと思います。
3. コンパクトリーマン面と周期の定義
前節でざっくり説明した「周期」ですが、正確に定義しようとするともう少し詳しい説明が必要です。
代数曲線 の周期とは、
のサイクル
を
上の微分形式
で積分したものとして定義されるのですが、この辺の概念を理解するためには複素多様体やリーマン面に関する知識が必要です。
というわけで、ここからかなり抽象的な話になります。正直に言うと、以下の話は私がほとんど理解していない内容で、不正確なものが多いかと思います。話半分に聞いていただいて、より正確な内容は参考文献の内容をご確認いただくようお願いします。
を2変数多項式として、
の形で定義される曲線を(平面)代数曲線といいます。一般に特異点を持たない代数曲線は、射影化するとコンパクトリーマン面になることが知られています。
非特異射影代数曲線の圏とコンパクトリーマン面の圏、さらに1変数代数関数体の圏は互いに圏同値になることが知られていて、これを三位一体というそうです。
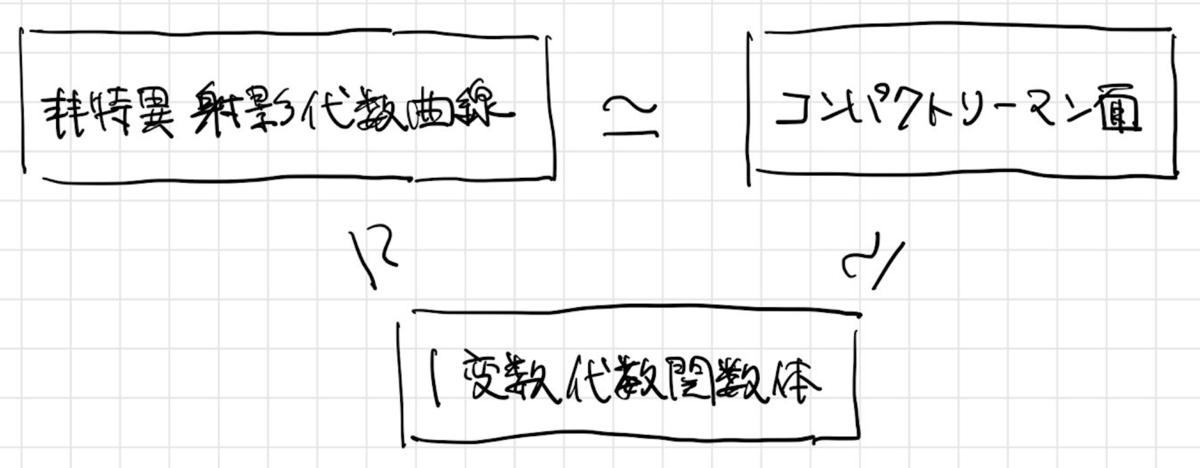
この圏同値を通して、非特異射影代数曲線をコンパクトリーマン面だと思います。以下では、リーマン面に関して今回の話に必要な材料をさらっと紹介することにしましょう。
以前、ド・ラームコホモロジーを紹介するにあたって、可微分多様体を導入しました
tsujimotter.hatenablog.com
可微分多様体は、雑にいうと「位相空間に の座標が張り付いていて、座標変換のルールを与える関数が無限回微分可能」なものでした。
可微分多様体の定義において、 の代わりに
、「無限回微分可能」の代わりに「正則関数」と置き換えたものを
次元複素多様体といいます。
特に としたものを リーマン面 といいます。つまり、位相空間に複素数平面の座標が張り付いたものをリーマン面というわけですね。リーマン面がコンパクトな位相空間であるとき、コンパクトリーマン面といいます。
は
上の2次元ベクトル空間だと思えますので、
はベクトル空間として
だと思うことができます。したがって、
次元複素多様体は、
次元の可微分多様体だと思うことができるわけですね。
さて のリーマン面は、
次元の可微分多様体だと思えるわけですが、特にこれを
次元の位相多様体(無限回微分可能の条件を外して、単に連続写像としたもの)だと思いましょう。つまり、多様体の形だけに着目するのです。
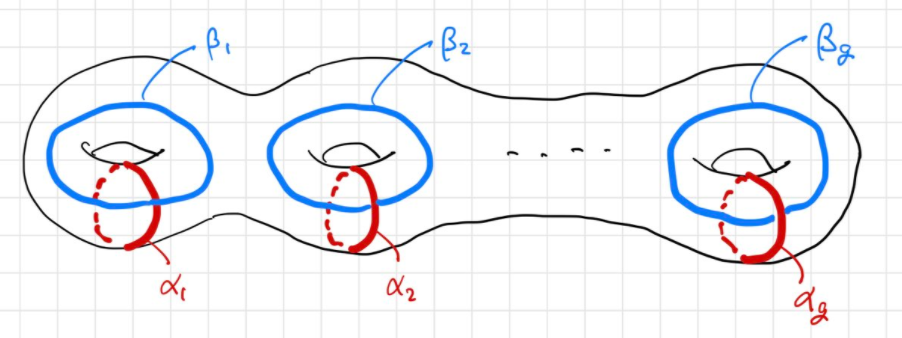
すると、その形は 種数 と呼ばれる非負整数によって分類されます。正確な定義はさておき、種数とは、多様体のもつ「穴の数」です。種数が0, 1, 2の例をあげるとこんな感じです。

こんな風にコンパクトリーマン面は穴の数によって分類できるというわけですね。コンパクトリーマン面 の種数を
と書くことにします。
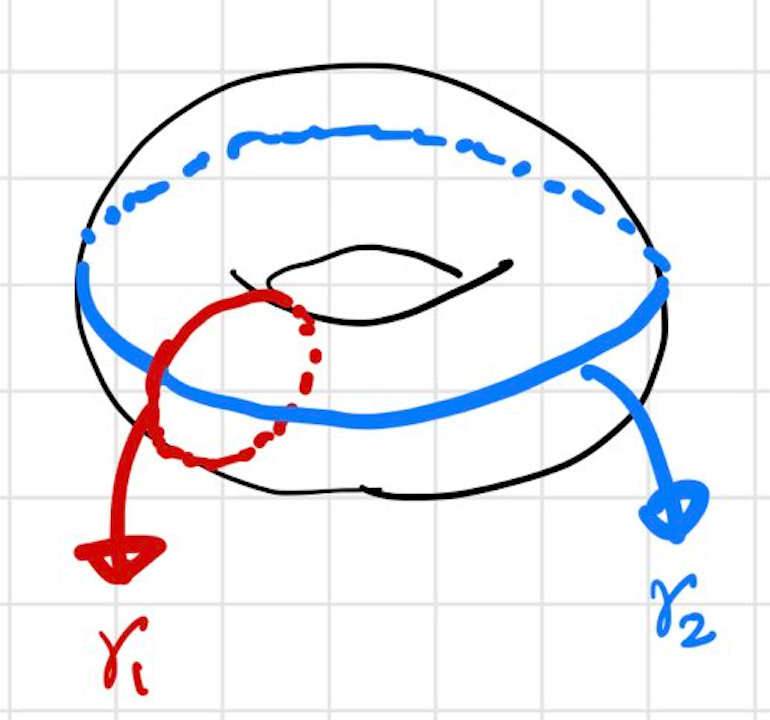
位相空間 はホモロジー
という不変量を持っています。今回使うのは1次のホモロジーなので
だけ考えます。これはサイクル全体のなす自由加群をバウンダリーで割った群です。サイクルとは
における閉曲線のことです。
たとえばトーラス には図のような独立な2本のサイクルがあり、これが
の基底となります。
の種数を
とすると、
の独立な自由基底の個数は
個 になることが知られています。種数が増えれば増えるほど、独立なサイクルが増えるわけですね。
後の目的のために係数 を
に拡大したものを
加群のテンソル積として
として定義します。体 でテンソルすると
ベクトル空間になるので、
の
ベクトル空間としての次元は
となります。
一方で、リーマン面は 次元の可微分多様体でもあるため、その上の微分形式を定義することができます。
によって
と
を同一視すると、複素関数
は2つの実関数
によって
と表すことができます。したがって、複素関数 は
として、2つの実変数
の関数だと思うことができるわけですね。
実は、もう一つ変数の置き方があります。 に対して
とおくと、上の関数は
の2変数関数だと思うことができます。変数
の代わりに
を使うことにするのですね。
任意の1次微分形式は、複素関数 を用いて
と表すことができます。 という形のものを正則微分形式、
という形の微分形式を反正則微分形式といいます。
のド・ラームコホモロジー
は、
上のベクトル空間として
と表すことができます。これをホッジ分解というそうです。
は正則微分形式のなす(
上の)ベクトル空間で、
は反正則微分形式のなす(
上の)ベクトル空間です。
がコンパクトなケーラー多様体のときは、正則微分形式と反正則微分形式が同型であることも知られています。(特に次元が一致します)
ここで、ホモロジーの元 とド ・ラームコホモロジーの元
に対して
という積分を定義することができます。特に、 が正則微分形式であるとき、上の積分を 周期 と呼びます。
リーマン面上の「サイクル」で積分していて、まさに周期という感じがします。
さて、上の積分はペアリング
を与えます。(ホモロジーの方は のように係数を拡大しています。)
を固定すると
なる対応が得られるので、これは線形写像
を誘導します。この線形写像が同型写像になるというのが、いわゆる ド・ラームの定理 です。
この同型により、ド・ラームコホモロジー の(
上の)次元とコホモロジー
の(
上の)次元が一致します。また、コホモロジーの(
上の)次元とホモロジーの(
上の)次元(
)も一致するので、
が得られます。これにより、正則微分形式のなす空間の( 上の)次元が
であることも言えます。
少し具体的な計算をしましょう。
たとえば、楕円曲線 の場合、
は種数 1 のコンパクトリーマン面、すなわちトーラスになります。この場合、正則微分形式の空間は(
上)1次元で、すべて
の
倍となります。また、トーラス上の独立なサイクルは
の2つなので(上の図を思い出しましょう)、
の上で
を積分した値
が周期となります。これを楕円周期と呼びます。
4. フェルマー曲線上の周期
以上の一般論を元に、フェルマー曲線上の周期について考えましょう。
フェルマー曲線 の
有理点全体の集合
は、代数曲線の一般論によりコンパクトリーマン面となります。
とすると、
の種数
は
であることがリーマン・フルビッツの公式を使って計算できます。
であれば
、
であれば
、
であれば
のような要領ですね。
前節で述べた通り、1次のド・ラームコホモロジーの( 上の)次元が
次元であり、特に正則微分形式のなす空間が(
上)
次元なので、上の公式により独立な正則微分形式の個数が計算できます。
そのような正則微分形式は、実をいうとすでに登場しています。なんと、 なる整数
に対して
がその( 上の)基底になっているらしいのです。
フェルマー曲線 には、次のような自己同型写像
があります。ここで は1の原始
乗根です。
(これが自己同型になっていることは、実際に代入してみればわかります。)
これらを に作用させると
となることが、これまた代入することによりわかります。
一般に、整数 に対して
が成り立つわけですね。
つまり、 は線型作用素
に対する固有値
の固有形式ということです。
はそれぞれ異なる固有値を持つので、独立な基底を定めるということみたいです。
ひとまず の組の個数が、種数の公式
の
に一致することを確認してみましょう。
のとき:
を満たす
は
のみです。したがって
となりますが、上で計算した種数の値
と一致しています。
のとき:
を満たす
は
のみです。したがって
となりますが、上で計算した種数の値
と一致しています。
上では具体例で確認しただけですが、これは一般にも成り立ちますね。
のとき、
のとき、
のとき、
のように1個ずつ組み合わせが減っていきます。よって、等差数列の公式により
と計算できますね。
さて、フェルマー曲線上の任意のサイクル における
の積分
を考えましょう。これが前節で定義した周期です。
なお、第2節で導入した
も、 内の「
というサイクル」における積分と思うことができ、これも周期だと言えますね。
準備が整いましたので、フェルマー曲線上の周期に関する、大変興味深い公式を紹介しましょう。今日はこれを紹介するために頑張って説明してきました。
ここまで読んでくれた方には、面白がってもらえることでしょう。
つまり、フェルマー曲線上のあるサイクル上で積分して得られる周期は、ベータ関数 に「
次円分体の元」をかけたものとして表せるということです。これが冒頭で述べた、フェルマー曲線上の周期とベータ関数の関係です。ベータ関数すごいですね!
この定理はGrossの以下の論文のAppendix内にて、Rohrlichによって解説されています。
Gross, "On the Periods of Abelian Integrals and a Formula of Chowla and Selberg", Inventiones maths, 45, pp. 193 - 211 (1978).
https://link.springer.com/article/10.1007%2FBF01390273
これが初出なのかはわかりませんが、Appendixに書いてあるというのが面白いですね。
上の定理では「あるサイクル」とぼかして書いていますが、Rohrlichの定理はもう少し具体的に書かれています。
フェルマー曲線には上で述べたような という自己同型があります。この自己同型はサイクルにも作用し、
は
加群となります。さらに、
加群として巡回的であるそうです。その生成元を
とすると、整数
に対し
と表せるサイクルに対して、周期が次のように計算されるというのが主張です:
詳しくは論文本体をご覧ください。
係数として の数が現れますが、背景には
のヤコビ多様体
の既約部分が
に虚数乗法を持つアーベル多様体となり、
は
のCM周期となっていることが背景にあるそうです。
CM周期の話も理解できたら楽しそうだなと思っています。
というわけで、今回はベータ関数とフェルマー曲線の関係について紹介しました。ベータ関数の特殊値は、フェルマー曲線の周期という量を考えるにあたって、非常に本質的な量になっているということですね。
実は、ベータ関数については、あと2個ほど書きたい内容があります!近々公開できると思うので、お楽しみに!(ベータ関数、面白いですね!)
それでは、今日はこの辺で。
参考記事
最初に興味を持ったきっかけは、梅崎さんの下記のスライドでした。
speakerdeck.com
それから加塩先生による一連のPDF記事を見つけ、その冒頭部分に関連する内容が書かれていることを知りました。以下の記事は大変参考にさせていただきました。
http://www.kurims.kyoto-u.ac.jp/~kenkyubu/bessatsu/open/B25/pdf/B25_002.pdf
https://www.rs.tus.ac.jp/a25594/20190330.pdf
https://www.rs.tus.ac.jp/a25594/20170529-0602.pdf
https://core.ac.uk/download/pdf/39312735.pdf
複素多様体やその上の微分形式については、以下の「コホモロジー」という本の「第5章 ケーラー多様体のホッジ理論とスキーム理論」を参考にしました。
フェルマー曲線の種数公式等の話については、こちらの記事を参考にしました。
http://www.math.sci.hiroshima-u.ac.jp/~m-mat/TEACH/TEACH/kyokusen1.pdf
