微分方程式には色々な種類があって、それぞれ解き方が異なったり、そもそも解けなかったりします。
理系大学生であれば大学1・2年でさまざまな微分方程式の解き方を習うわけですが、これは微分方程式の中でもほんの一部である「うまく解ける微分方程式」の解き方を学んでいるにすぎません。タイトルにある 完全微分方程式 は、そのような常微分方程式の一種です。
を
級(1階偏微分可能かつ1階偏導関数が連続な)2変数実関数とします。このとき
の形の微分方程式を考えます。
加えて 完全微分形 という条件を考えます。この条件を満たすかどうかで、式 の微分方程式の解き方が変わります:
微分方程式 が完全微分形の条件を満たすとき、完全微分方程式 といいます。
(満たさない場合は「不完全微分方程式」といって、取り扱いが異なってきます。こちらについては今回は扱いません。)
完全微分形の条件を満たすとき、次が成り立つことが知られています:
が成り立つ。
また、このように書けるのは完全微分形のときに限られることもわかります。すなわち、式 が完全微分形であるための必要十分条件というわけですね。この事実は超重要なので、次節で証明したいと思います。
実際、完全微分形の条件を満たすとき であり、また式
から
なので、合わせて
が言えます。よって、定数 を用いて
が言えることになります。これは、元々の完全微分方程式 を満たす
の組を陰関数によって表現した方程式になっており、これが微分方程式の解と言えるわけです。
これが完全微分方程式 の解法だったわけでした。
ここからが今日の本題です。完全微分方程式を解くために必要であった条件は、まさに 上の ド・ラームコホモロジー を計算する際に必要な条件そのものであった、というのが今日話したい内容です。すなわち、完全微分形の必要十分条件は
を表しているのです。
今回の記事では、前半で完全微分方程式の必要十分条件の証明を行います。後半では、この条件がまさに、ド・ラームコホモロジーにおける条件を表していることを具体的な例を元に説明したいと思います。
目次:
(準備)線積分とグリーンの定理
2次元平面 の中で与えられた経路に沿って足し合わせる積分を考えたいと思います。こういう積分を「線積分」といいます。経路を
として
というような積分を考えたいわけです。
ここでは、経路 が
で与えられているとしましょう。 は区間内において
級であるとします。

このとき、曲線 上の線積分を
によって定義します。これで右辺は普通の1変数の積分ですから、計算はできますね。
同様に
のように定義することができます。
足し合わせると、こんな積分
も計算することができます。
ここで、パラメータの選び方によって積分の値が変わってしまうのではないかという心配が生じると思うのですが、上記の積分は曲線 を区分することによって直接的に定義することもでき、これと一致することが示せます。
ひとまず、線積分とは被積分関数と経路 が与えられたら、積分値が得られるものだと思っていただければと思います。
このように定義された線積分を、重積分に置き換えることができるというグリーンの定理が知られています。
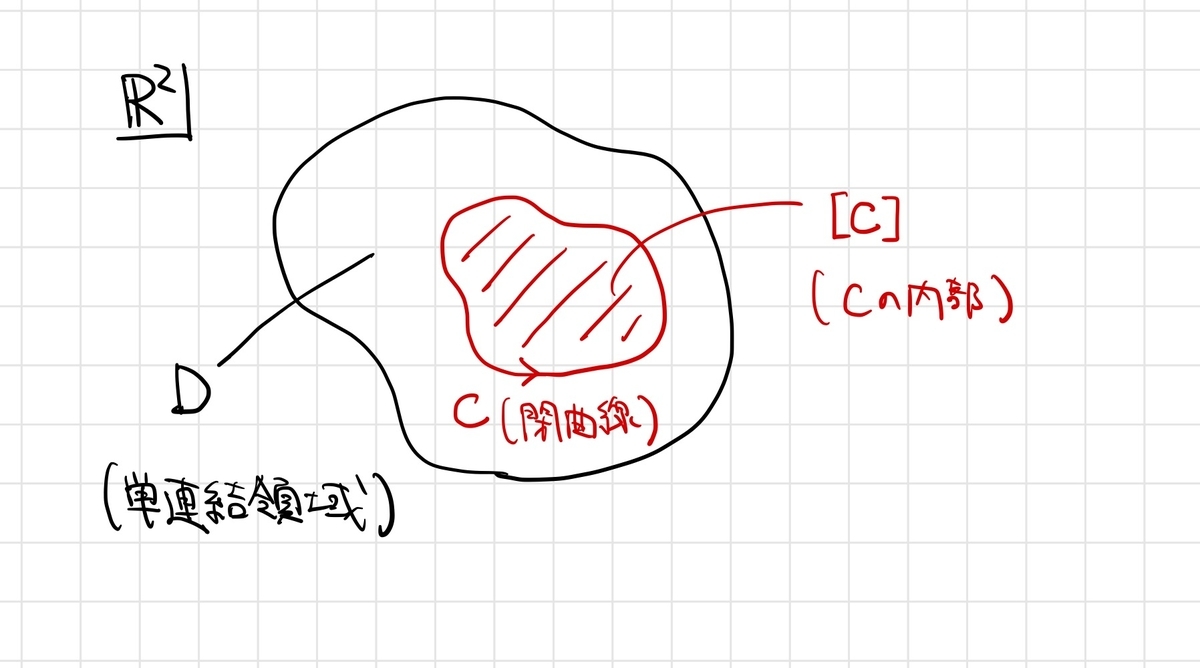
ぐるっと一周する経路(これが「閉」曲線の意味するところですが)における線積分を、その内部の面積分に置き換えるという定理というわけですね。
ここでは、グリーンの定理は単連結な領域内だけで成り立つ話であるということを強調しておきます。領域 が単連結であるとは、
内の任意の閉曲線(ぐるっと1周して戻ってくる経路)の内部が
の点のみであるということを意味します。

ここで気にすべきことは の定義域です。たとえば、
が原点で
級でなかったとしましょう。この場合、グリーンの定理を適用しようと思うと、領域
としては「原点を含むものを取れない」わけですね。当然、無理やり原点の周りを一周する経路
を考えたとしても、積分値は右辺の重積分の値とは一致しません。この辺が、後半の計算例で実際に出てきます。
完全微分形の必要十分条件
それでは、グリーンの定理を使って次を示したいと思います。
この定理を示すことができれば、完全微分方程式が解けることは前節で説明しました。
を示すのは簡単です。逆に、
を示すのが難しいわけですが、ここにグリーンの定理を使います。証明の 一番ポイント はこちらです。
が成り立てば、線積分によって 上の関数を作ることができる
上のポイントについて補足的に説明しておきましょう。グリーンの定理の右辺に を代入すると
が得られます。これはつまり、領域内の閉曲線 で
を積分すると、積分値が
になるということです。
ここで 内の2点
に対して、
から
への2種類の経路
を用意します。
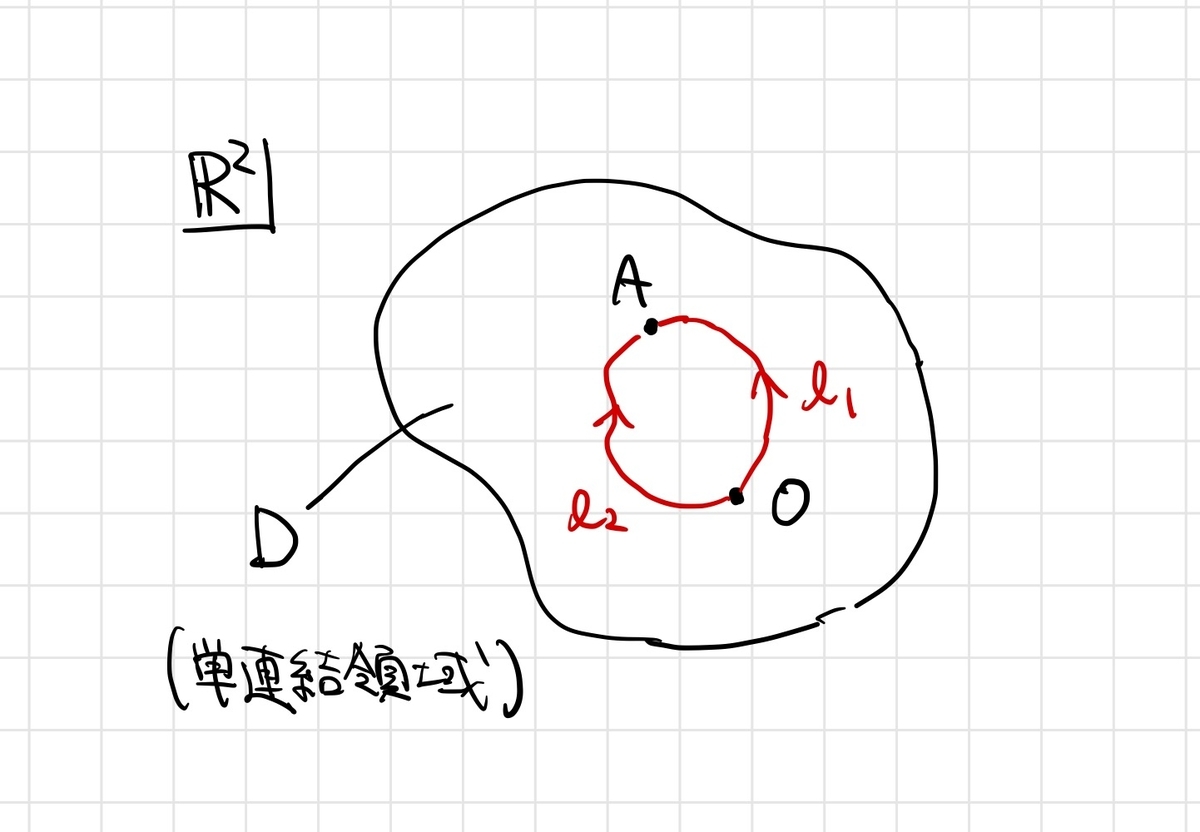
に対して
を逆転させた経路
を繋げた
を考えると、点
から
を経由して
に戻る閉曲線が得られます。よって
が得られますが、曲線を分けて積分を分割すると
となります。これはつまり、 から
への
の積分は、経路によらず同じ値を取るということです!!
同じ値をとるということは、始点 を固定してしまって、終点
の座標を
とすれば、
となり、線積分によって新しい関数 を作ることができるというわけですね。面白いですねー!!
このようにして得られた関数 は、後で示すように偏微分可能でもあり、さらに偏微分して得られた関数は連続関数になります。すなわち、
級関数になります。
実はこの が求めたい関数であったということになります。
それでは証明にいきましょう。
(証明)
の証明:
与えられた に対して全微分の定義に従って計算すると、
となる。よって、
と合わせると
が成り立つ。ここで、 を計算すると
となり、 が得られた。
の証明:
グリーンの定理と により、
内の任意の閉曲線
において
が成り立つ。ここで 内の1点
を固定し、
内の点
までの経路を
とすると、積分
は積分経路 によらず一定の値をとる。そこで、この積分を用いて
と表すと、 は
上の関数として定まる。
さて、ここで を
方向に
だけ動かしたものを考える。
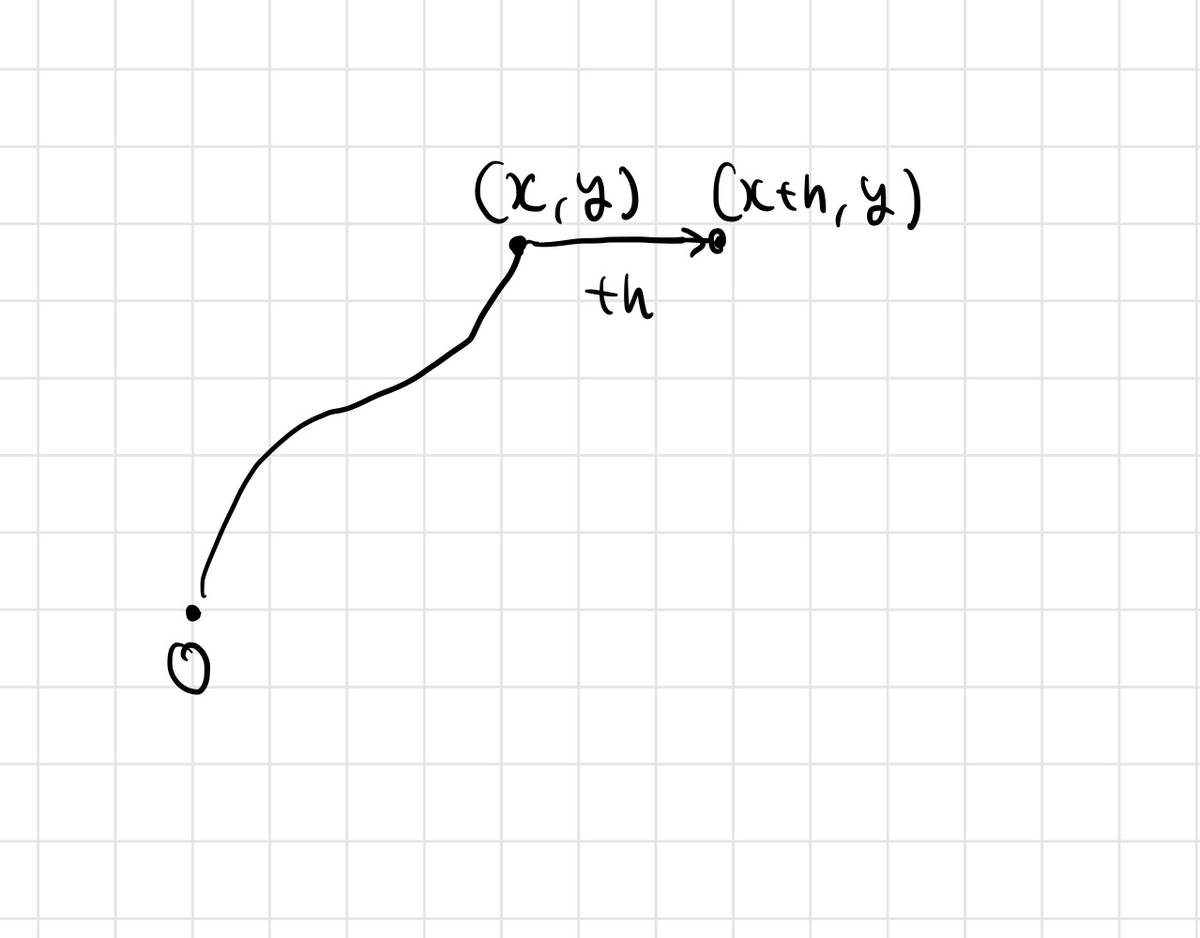
このとき
であるが、この積分経路においては の変化はないので、右辺の積分は
だと思える。この積分においては は定数だと思えるので、
についての1変数関数として考える。
は
級なので、
についての平均値の定理により、ある
が存在して
が成り立つ。 の連続性より
が成り立つ。同様に
も成り立つことがわかる。
よって、 は
上の
級関数であり、その全微分は
となることがわかった。これは求める関数である。
そんなわけで、完全微分形の条件
が成り立つときには、冒頭の議論によって完全微分方程式に解が存在するということが証明されましたね。
ド・ラームコホモロジーとの関係
ここからは、上で述べた条件が、まさにド・ラームコホモロジーの完全性に関わっている話をしたいと思います。具体的に、単連結な場合とそうでない場合において、ド・ラームコホモロジーを具体的に計算することで、そのことを実感したいと思います。
微分多様体やド・ラームコホモロジーの定義については、過去に書いた下記の記事を参考にしてください。
tsujimotter.hatenablog.com
この記事で必要な部分に関して、ド・ラームコホモロジーの簡単な復習をしたいと思います。
そもそもド・ラームコホモロジーは多様体の上で定義される概念ですが、今回はもっとも簡単な多様体の例として、 内の領域に限定して考えましょう。
内の領域は恒等写像によって
内の領域と同相なので、多様体であることは明らかですね。
いくつか用語を定義しておきましょう。
一般に を
内の領域とします。
上の
級関数全体のなす
ベクトル空間を
とします。
次に、 上の任意の
級関数
を用いて
と表せる微分形式を 上の
級1形式といいます。
上の
級1形式全体のなす
ベクトル空間を
とします。
同様に、 上の任意の
級関数
を用いて
のように表せる微分形式を 上の
級2形式といい、
上の
級2形式全体のなす
ベクトル空間を
とします。
ここで、 の間には外微分と呼ばれる写像が定義できます。
を
によって定義します。また、 を
によって定義します。
これらは 上の線形写像であり、
を満たします。
ここで
と定義します。どちらの集合も1形式全体の空間 の部分空間になっています。
の元を閉1形式、
の元を完全1形式、
より
であることがわかります。よって商ベクトル空間
を、 上の1次のド・ラームコホモロジーというのでした。
駆け足になってしまいましたが、必要な概念の定義は終わりました。ド・ラームコホモロジーの定義はなかなか難しいですが、その意味するところは「閉形式と完全形式の差」を表しています。一般に
ということになりますが、もし閉形式がすべて完全形式なのであれば、ド・ラームコホモロジーは一点に潰れてしまいます。
閉形式であって完全形式でないものが存在すれば、それはその空間特有の興味深い対象ということになり、ド・ラームコホモロジーの非自明な元となります。こんな風に、ド・ラームコホモロジーは舞台となる空間の情報を持っています。
実際、この辺は計算してみるとより理解できると思いますので、2つの例の計算を実行してみましょう。
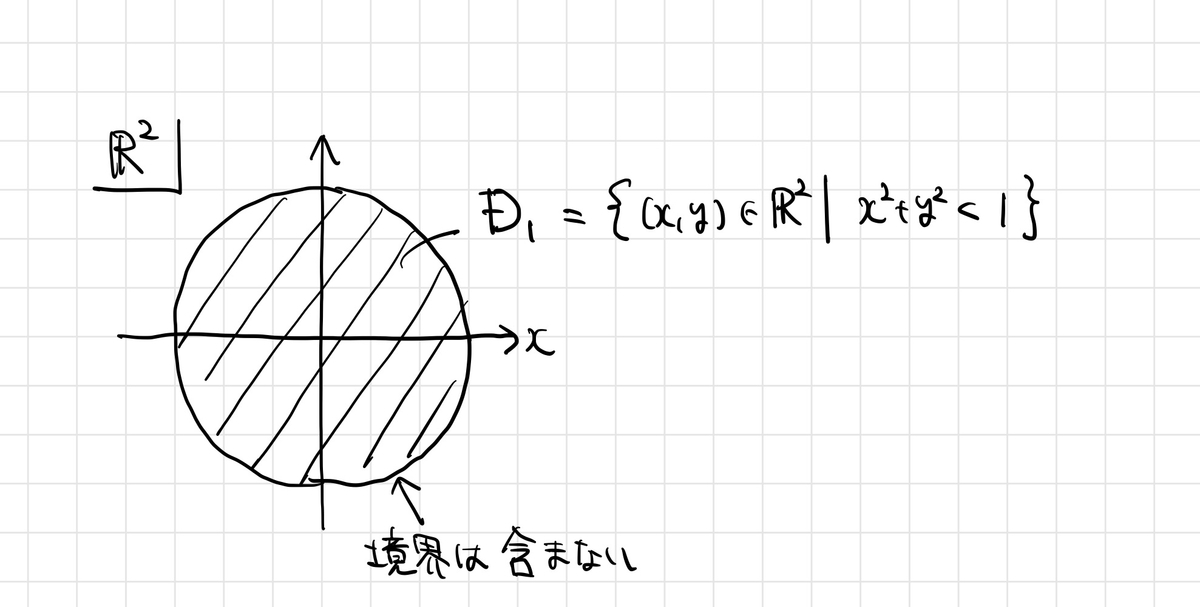
例1:単連結な開円板
ここからは 内の単位開円板
を考えて、 上のド・ラームコホモロジーを考えることにします。
は単連結な領域の例になっていますね。
さて、 上の閉1形式(
の元)が完全1形式(
の元)になっているかどうかを考えたいわけですね。
任意の閉1形式 を考えます。
は1形式なので、
級関数
を用いて
と表します。外微分の定義より、 ということになりますので、外微分の定義を展開すると
ということになります。これはつまり、 に対して
が成り立つということです。
あれ? これはどこかでみたことのある条件ですね。
そう、これは完全微分形の条件そのものですね!
定理2(完全微分形の必要十分条件)より、条件 が成り立つとき、ある
上の
級関数
が存在して
が成り立ちます。実際、このような関数は、固定した点 から点
まで
を積分して得られることを思い出しましょう。
さて、これにより と表すことができたわけですが、これは
の
による像が
であることに他なりません。したがって、
、すなわち
は完全1形式だったというわけです!
元々 は任意の閉1形式でしたが、これが完全1形式でもあるということがわかったわけですね! すべての閉形式が完全形式というわけなので、
上の1次ド・ラームコホモロジー群は
ということになります。
完全微分形の必要十分条件は、まさに閉形式が完全形式であることを表す条件だったわけですね!
なお、今回は を単位開円板としましたが、
内の単連結な領域であれば、まったく同じ結果になりますね。
例2:穴あき開円板
上では単連結な例を考えましたので、単連結でない例を考えましょう。単位開円板から原点 を除いたものを
としましょう。
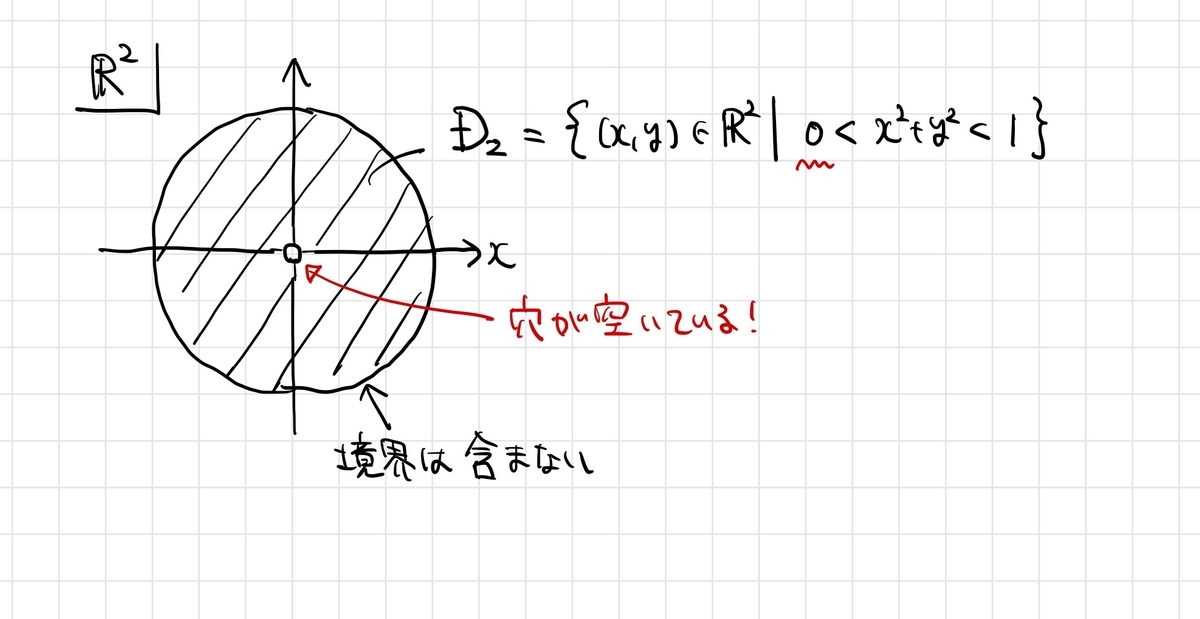
このとき、 上の閉1形式
を考えます。これは例によって、
上の
級関数
を用いて
と表されます。
ここで、 は
上であれば
級ですが、原点
では何も条件が課されていないことに注意します。もし、
においても
級であれば、例1のときとまったく同じ議論により完全形式となります。
したがって、 上で
級、かつ、原点
において
級ではないものが、1次ド・ラームコホモロジー群の非自明な元を生成することになります。
たとえば
は 上
級関数ですが、
で連続ではありません。
また
より
となりますので、1形式
は 上の閉1形式の例になっていますね。
問題は、これが完全1形式であるかです。すなわち、 となるような
級関数
は存在するのでしょうか。実際、存在しないと思うのですが、私の力ではそれを示すことができそうにありません。どうやったらいいんですかね・・・。
と思っていたら、考え方を見つけました。
https://www.math.nagoya-u.ac.jp/~larsh/teaching/F2014_G/lecture.pdf
今、 となるような
上の
級関数
が存在すると仮定しましょう。
積分経路を として「半径
の円周を左回りに回る経路」をとり、線積分
を2通りの方法で計算します。
まず、積分経路 上の座標を変数
を用いて
のように置くと、上記の線積分は
と表せます。これは に関する1変数の積分なので、
とおいて計算すると
となり積分値は となります。
一方、連鎖律を用いて被積分関数内の微分を計算すると
となります。これを線積分に代入すると
となり、積分結果が矛盾します。
したがって、「 となるような
上の
級関数
が存在する」という仮定が誤りであったとわかります。
こんな風に、ド・ラームコホモロジーの非自明な元 を得たわけですが、他にも非自明な元はあるかもしれません。いったい何次元の空間なのでしょうか。
実際、ド・ラームの定理 というものがあって、位相空間のコホモロジーとの間に線形同型があります。すなわち
が成り立ちます。ここから、 であることがわかるので、結果として
が1次元
ベクトル空間となります。この基底の代表元として、先ほどの
が取れるということですね。
にはまさに穴が空いていて、単連結ではないことを表すのが、この
であると言えそうですね。
おわりに
今回は、微分方程式の解き方に現れる 完全微分形の必要十分条件 について考えました。
この条件は、 であることと、
なる
が存在することが同値であるというものでした。証明には、グリーンの定理を使いましたが、
の定義域の単連結性がポイントでした。単連結な場合には、完全微分形の条件が成り立つならば、2点間をつなぐ経路上のとり方によらず、
の積分が計算できるということでした。よって、その積分によって関数
が定義できたというわけですね。ここが本当に面白かったですね。
さらに、この条件はまさにド・ラームコホモロジーにおける
なる必要十分条件の、まさに言い換えになっているということでした。これにより単連結領域上であれば、1次のド・ラームコホモロジーは自明になってしまうということでした。
ド・ラームコホモロジーは一見抽象的な概念に見えるかもしれませんが、結局は「与えられた関数(微分1形式)が積分可能であるか」を見ている群だということですね。完全形式であれば積分可能というわけです。
いやー、いろいろ繋がってきて面白いですね!
それでは今日はこの辺で!
追記(2020.02.22):穴あき円板のド・ラームコホモロジーの直接計算
の場合について、
がド・ラームコホモロジーの基底となることを「直接的に」計算する方法が分かりましたので、別の記事にまとめました。
tsujimotter.hatenablog.com

