自由研究：有理数に収束する級数を探せ！（超幾何級数の面白い応用）

突然ですが「無理数」って面白いですね！この分野には未解決問題もたくさんあり、魅力的なトピックがたくさん詰まっています。

今日はその無理数をきっかけに tsujimotter が考えることになった、ちょっと変わった興味深い問題についてご紹介します。

きっかけは、tsujimotter が先日発表した「無理数とお友達になろう」というプレゼンでした。

無理数とお友達になろう - 第384回科学勉強会 from Junpei Tsuji

www.slideshare.net

70スライドに渡って色々なことを語りまくったのですが、発表の中で特に伝えたかったメッセージは『「無理数であるか有理数であるかどうか」を知ることは、数を理解する上で本質的である』という点です。

無理数は、潜在的にある種の無限性をもっています。たとえば、ネイピア数 $e$ は典型的な無理数ですが、以下のように無限級数で表現できます。

$\displaystyle e = 1 + \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \frac{1}{4!} + \cdots$

この級数はこれ以上簡単にすることができず、したがって有限回の手続きで計算することが出来ないのです。一方で、有理数であれば分数の形で表すことができ、その手続きは有限に閉じています。

したがって、「無理数であるか有理数であるか」を知ることは、「その数をどこまで理解可能か」を知るために必要な所作であるといえます。

このことを具体的な例で説明するために、「有理数だけど無理数っぽく見える数」の例を作ることを試みました。《一見これ以上計算できないようにみえる無限級数》が出来れば、その級数で表せる数は《無理数っぽく》みえますよね。

さて、ここで１つ問題が生じます。「有理数に収束する無限級数」をいったいどうやったら作ることが出来るでしょう。そのような一般的な方法はあるのでしょうか。

無限級数で表せる数としては、たとえば $2$ に収束する無限級数がよく知られています。

$\displaystyle 2 = 1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \cdots$

このままでは「整数に収束する級数」ですので、収束先を有理数にするために、両辺に $\frac{1}{3}$ をかけてあげましょう。すると、

$\displaystyle \frac{2}{3} = \frac{1}{3} + \frac{1}{2\cdot 3} + \frac{1}{4\cdot 3} + \frac{1}{8\cdot 3} + \frac{1}{16\cdot 3} + \cdots$

のように、「有理数に収束する無限級数」を作ることが出来ます。

しかし、なんというか、これでは風情がありませんね。 $\frac{1}{3}$ の部分をつくるために、むりやり $3$ で割った感じがバレバレです。人工的すぎるのです。

もっと自然に、有理数に収束するような級数はないか。もっといえば、その収束先がすぐ計算できないようにしたい。

このような問題に対する一般的な方法は、tsujimotter が探した限りでは見つかりませんでした。ありそうでないのですね。

というわけで、頭を使って考えました。

本記事では、私が試行錯誤してなんとか見つけた以下の２通りの方法について、ご紹介したいと思います。

等比級数を用いる方法
超幾何級数を用いる方法

とくに２番目の方法は、非常に面白いので期待してご覧ください。

等比級数を用いる方法

級数を作ろうと考えたときに、真っ先に思い浮かぶのは関数 $f(x)$ のテイラー展開です。

ただし、 $f(x)$ はどんなものでもよいわけではなく「関数値が有理数」という条件があります。もし $f(x)$ が $x$ についての有理関数であれば、有理数 $\alpha$ を入れると自動的に関数値 $f(\alpha)$ が有理数になるはずです。

これをふまえて、有理関数のテイラー展開を考えましょう。少し調べれば $\displaystyle f(x) = \frac{1}{1-x}$ の展開がその条件に該当することがわかります。この式の展開は、以下のような無限級数となり、いわゆる等比級数になることがわかります。

$\displaystyle \frac{1}{1-x} = 1 + x + x^2 + x^3 + \cdots$

ただし、右辺が収束するのは $\left|x\right| < 1$ のときだけなので、 $x$ に代入できるのはこの条件のものだけです。

この式に $x = \frac{1}{2}$ を代入すると、冒頭で挙げた級数を得ることが出来ます。

$\displaystyle 2 = 1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \cdots$

ほかにも、この式に $-1 < x < 1$ となる有理数 $x$ を代入してあげることで、似たような級数をいくらでも生成できるのです。たとえば、 $x = -\frac{1}{9}$ を代入すると、以下の式が得られます。

$\displaystyle \frac{9}{10} = 1 - \frac{1}{9} + \frac{1}{81} - \frac{1}{729} + \cdots$

これにて、有理数 $\frac{9}{10}$ に収束するそれっぽい級数を作ることが出来ました。今回のスライドでは、この級数を説明に採用したのでした。

一方で、等比級数を用いた方法には、個人的には少し不満があります。なぜ不満かというと、右辺の級数が簡単に計算できてしまうからです。

高校数学に慣れた人が見ると、右辺の形はどうみても等比数列の和です。したがって、和の公式を当てはめれば、即座にこれが $x = \frac{9}{10}$ であることがバレてしまいます。これは面白くないですね。

というわけで、この「級数が簡単に計算できてしまう」という問題を解消するために、二番目の方法に移りましょう。

超幾何級数を用いる方法

二番目に紹介する方法は「一見無理数にみえるような無限級数であり」なおかつ「級数が簡単に計算できない」という素晴らしい方法です。

とはいえ、発表スライドを作っている段階では、この方法はまったく頭にありませんでした。

等比級数の方法があまりしっくりこなかったため、しばらく「どうしたもんかなあ」と悩んでいたのですが、フォロワーである @triprod1829 さんから素晴らしいアイデアをいただいたのです。それが、「超幾何級数」を用いた方法です。

超幾何級数は Wikipedia にも載っていますので、まずは調べることから始めましょう。

超幾何級数 - Wikipedia

冒頭部分に書かれた $F(a, b, c; z)$ が今回用いる超幾何級数の式です。 $F$ は $a, b, c, z$ の４変数関数になっています。

変数の数が多いので、おどろおどろしい姿にみえますね。超幾何級数はガウスによって研究されていたことで知られています。たとえば、五次方程式の超越的な解を求めるためにも使われていたりするそうです。

その意味で tsujimotterもいろんな場面で見かけてはいたのです。しかしながら、この厳めしいフォルムに「得体の知れないエイリアン」に出会ったようなそんな気持ち悪さを感じて、どうしても親しみがもてないでいました。簡単にいうと、避けていたのです。

f:id:tsujimotter:20150807204307p:plain:w300

今回は、勇気を出して踏み込んでいきましょう。

改めて定義を書いていきましょう。以下の式の右辺が超幾何級数と呼ばれる級数です。

$\displaystyle F(a, b, c; z) = \sum_{n=0}^{\infty}\frac{(a)_n (b)_n}{(c)_n n!} z^n$

右辺の $(x)_n$ の部分は「ポッホハマー記号」というらしく、以下の式で定義されます。

$\displaystyle (x)_n = \prod_{k=0}^{n-1} (x + k)$

積記号は、 $x$ からはじまって、 $x, x+1, x+2, \ldots$ と順に $n$ 個の数の積をとります。

ポッホハマー記号の例を挙げると、 $x = 3, n = 4$ のとき、

$\displaystyle (3)_4 = (3+0)(3+1)(3+2)(3+3) \\ \displaystyle \hspace{15pt} = 3\cdot 4\cdot 5\cdot 6$

となります。

見た目は複雑な超幾何級数ですが、計算は思いのほか単純で、機械的に計算することができます。

たとえば、 $a = 1, b = 1, c = 4$ を入れると、以下のようになります。

$\displaystyle F(1, 1, 4; z) = \frac{1\cdot 1}{1 \cdot 1}z^0 + \frac{1\cdot 1}{4\cdot 1!}z^1 + \frac{(1\cdot 2)\cdot (1\cdot 2)}{(4\cdot 5) \cdot 2!}z^2 \\ \displaystyle \hspace{81pt}+ \frac{(1\cdot 2\cdot 3)\cdot (1\cdot 2\cdot 3)}{(4\cdot 5\cdot 6) \cdot 3!}z^3 + \cdots \\ \displaystyle \hspace{40pt} = 1 + \frac{z}{4} + \frac{z^2}{10} + \frac{z^3}{20} + \cdots$

ところで、このままではこの級数がどの値に収束するか分かりませんね。ここで使えるのが、ガウスによって発見された「超幾何定理」です。

《超幾何定理》
複素数 $a, b, c$ に対して、以下が成り立つ。
$\displaystyle F(a, b, c; 1) = \frac{\Gamma(c)\Gamma(c-a-b)}{\Gamma(c-a)\Gamma(c-b)}$

ただし、収束条件は $\text{Re}(a) + \text{Re}(b) < \text{Re}(c), \;\; c \not\in \mathbb{Z}\backslash \mathbb{N}$ である。

下に見えるものは収束条件です。１つめの条件は $a, b$ の実部の和が $c$ の実部より小さい。２つめの条件は、 $c$ は負の整数ではない。というものです。

結構複雑な式ですが、もともとの超幾何級数の定義では $a, b, c$ が複素数であることを想定しているため、こんなに複雑なのです。今回の用途では $a, b, c$ は整数なので、定理の式も収束条件も、もっと簡単になります。

たとえばガンマ関数は、整数 $n$ に対しては、

$\displaystyle \Gamma(n) = (n-1)!$

のようにふるまいます。

また、整数 $a, b, c$ の実部をとっても、整数 $a, b, c$ のままです。

以上をふまえて、 $a, b, c$ を整数におきかえると、以下のようになります。

《超幾何定理の言い換え》
整数 $a, b, c$ に対して、以下が成り立つ。
$\displaystyle F(a, b, c; 1) = \frac{(c-1)! (c-a-b-1)! }{(c-a-1)! (c-b-1)! }$

ただし、収束条件は $a + b < c, \;\; c > 0$ である。

ずいぶん簡単な形で表せました。

この式に $a = b = 1, c = 4$ を代入すると、

$\displaystyle F(1, 1, 4; 1) = \frac{(4-1)! (4-1-1-1)! }{(4-1-1)! (4-1-1)! } = \frac{3! 1! }{2! 2! } = \frac{3}{2}$

となります。ちゃんと有理数になりましたね。

結局、上の級数と合わせると、

$\displaystyle \frac{3}{\;2\;} = 1 + \frac{1}{4} + \frac{1}{10} + \frac{1}{20} + \frac{1}{35} + \frac{1}{56} + \frac{1}{84} + \frac{1}{120} + \frac{1}{165} + \frac{1}{220} + \cdots$

であることが分かりました。

この式を見ただけでは、右辺の級数が左辺の有理数値に収束するなど、まったく想像もつきませんね。

むしろ、本当にこの等式は合っているのだろうかと疑いたくなるかもしれません。念のため確認してみましょう。

最初の１０項に関して、１項ずつ足し合わせていき、 $\frac{3}{2}$ と比較したものが次のグラフです。

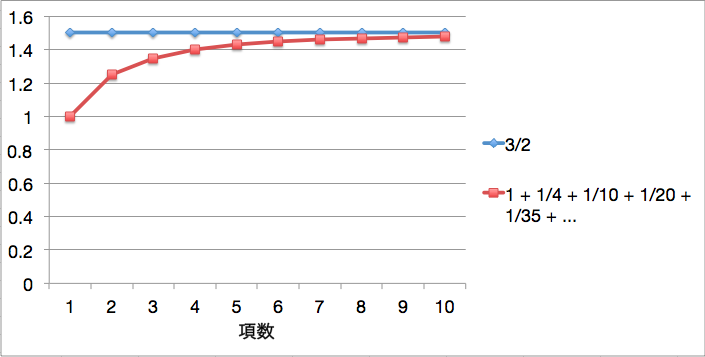
f:id:tsujimotter:20150806221217p:plain:w400

足し合わせる毎に、赤線（無限級数）が青線（ $\frac{3}{2}$ ）に近づいていっているのが見て取れます。これで、右辺の級数が $\frac{3}{2}$ に収束していることが、数値的にも確認できました。一安心ですね。

ほかにも、 $a, b, c$ の組み合わせを変えたいくつかのパターンで試してみましょう。

$a = 1, b = 1, c = 3$ の場合

$\displaystyle 2 = 1 + \frac{1}{3} + \frac{1}{6} + \frac{1}{10} + \frac{1}{15} + \frac{1}{21} + \frac{1}{28} + \frac{1}{36} + \frac{1}{45} + \frac{1}{55} + \cdots$

$a = 1, b = 2, c = 6$ の場合

$\displaystyle \frac{5}{\;3\;} = 1 + \frac{1}{3} + \frac{1}{7} + \frac{1}{14} + \frac{5}{126} + \frac{1}{42} \\ \hspace{60px} \displaystyle + \frac{1}{66} + \frac{1}{99} + \frac{1}{143} + \frac{5}{1001} + \cdots$

$a = 1, b = 2, c = 14$ の場合

$\displaystyle \frac{13}{\;11\;} = 1 + \frac{1}{7} + \frac{1}{35} + \frac{1}{140} + \frac{1}{476} \\ \hspace{60px} \displaystyle + \frac{1}{1428} + \frac{1}{3876} + \frac{1}{9690} + \frac{1}{22610} + \frac{1}{49742} + \cdots$

いずれの例も、右辺がとても左辺に収束するとは思えないような、不思議な等式となっています。面白いです。

以上の計算を簡便にするために、今回は Ruby のスクリプトを作りました。以下のページにあげたスクリプトを計算に用いています。

超幾何級数を計算するスクリプト · GitHub

ソースコードの $a, b, c$ を色々変えてみれば、自分でも試すことが出来ますので、Ruby の実行環境がある方はぜひやってみてください。

また、Ruby が使えない方でも、簡単に試せるように、次のようなサイトを作ってみました。ぜひ遊んでみてください。
tsujimotter.info

まとめ

今回は「有理数に収束する級数」を求めるための方法を２つ開発してご紹介しました。

２つめの方法は、「超幾何級数」というものを使った方法でしたが、まさかこんな応用があるとは私は思いもしませんでした。これまでにも、超幾何級数を見る機会はあって、存在を知ってはいたのですが、ただ得体の知れない存在という感じで、その変数の多さはまるでエイリアンのようでした。それぐらい遠い存在だったのです。

$a, b, c$ が整数で $z = 1$ のときに限っては、超幾何級数は単なる有理関数になってしまうのですね。これでこの級数に対して、ずいぶんと親しみが沸いたのではないでしょうか。