（小ネタ）恋する無限遠点

Aさん「私はBくんのことが大好き！」
Bくん「僕はその100倍好き！」
Aさん「じゃあ私はその1000倍好き！」
俺「y=100x,x=1000yだからx=y=0」

というネタがツイッターで流れてきたので、私も乗っかりたくなりました。

普通に実数上で上記の式を考えてしまうと になってしまうわけですが、たとえば とかで考えれば別の解が存在することになりますね。

以下のページで詳しく書いてありましたので、ご紹介します。

私はあなたのことがこんなに好き！ - ぷりんの雑記帳

さて、私の方はというと、これを「楕円曲線」で考えたくなったというわけです。

楕円曲線 上の任意の点には、自然に「加法（＋）」という演算を入れることができて「アーベル群」をなします。この場合の単位元 は「無限遠点」になります。

加法を 回繰り返せば 倍という写像も自然に定義できます。

また、 が に一致するとき、 を楕円曲線 等分点といいます。 回繰り返すと戻ってくるということですね。こんな風に戻ってくる点もあれば、二度と戻ってこない点もあります。戻ってくる点のことを「ねじれ点」と言ったりもします。

さて、先の問題に話を戻すと、彼女の愛情を点 とし、彼の愛情を点 とします。楕円曲線では 倍とか 倍とかを考えることができますから、先ほどの記事と同じ議論ができますね。

結果的に、3倍か41倍か271倍して になる、等分点を持つような楕円曲線を見つけてくればいいわけですね。

たとえば、

という曲線を考えて、この曲線に無限遠点を加えると楕円曲線になります。これを とすると、 にはたとえば という３等分点があります。

ははるか無限遠 なので、図には現れません。

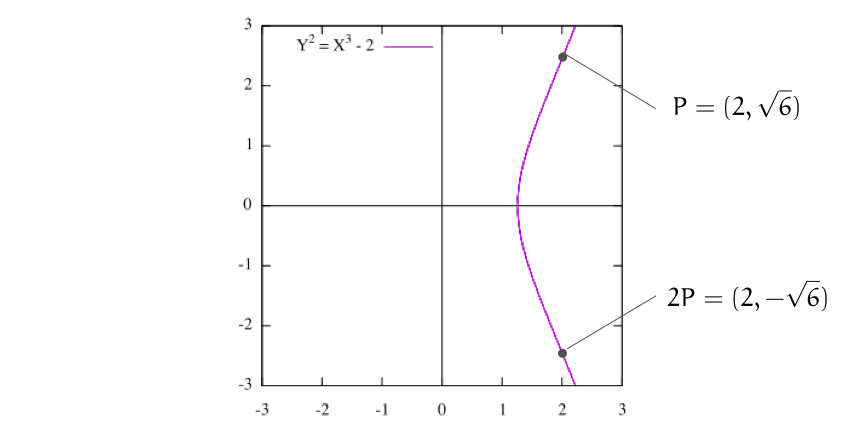
彼女と彼の点を としておけば、元の条件は成り立ちますね。

ところで、先の記事では を除いていましたが、ふと も許しても面白いんじゃないかと思いました。

なので 「彼も彼女も無限遠点にいる」ことになりますね。こっちの方が少しロマンチックな感じがしませんか？笑

無限遠点といえば、恋い焦がれる場所でもあります。

加藤先生・臼井先生というお二人の数学者の掛け合いによって生まれた、こんな川柳を思い出します。最後にご紹介して終わりにしましょう。

数学は 無限遠点 恋う心 恋うて焦がれて 遙かな旅路

それでは、今日はこの辺で。

おまけ

無限遠点で愛し合うカップルその２
togetter.com

参考文献

素数の歌が聞こえる (-)

楕円曲線論入門