「ユークリッド整域」ならば「単項イデアル整域」の証明

最近、「素数と2次体の整数論」という本の読書会をはじめました。

素数と2次体の整数論 (数学のかんどころ 15)

作者:青木昇
発売日: 2012/12/21
メディア: 単行本

主に数学デーというイベントの中で毎週１、２回程度開催して、少人数で濃い勉強をしています。「ゆるにじたい」という名前で開催しているのですが、基本的に全部の命題・定理の証明を追いかけるという感じでやっています。

先日は【有理整数環 $\mathbb{Z}$ が単項イデアル整域であること】を証明するパート（1.3節）を読みました。面白かったので紹介したいと思います。

読書会の前までは、今回の内容は「知っているつもり」でいて、実はちゃんと理解していないことでした。今回の勉強会でようやくちゃんと理解できるようになりましたので、自分の言葉でまとめてみたいと思いました。これがこの記事を書いた動機です。

といっても、本に書いてある証明をそのまま紹介はしません。本の証明は「有理整数環 $\mathbb{Z}$ 」に限定された証明なのですが、実はこの証明は「一般のユークリッド整域 $R$ 」に一般化することができます。

今日示したいことを図に表すと以下のようなイメージになります。

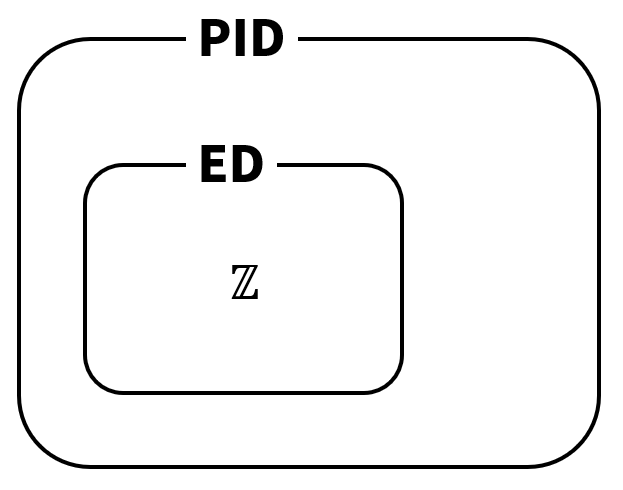
f:id:tsujimotter:20200317185847p:plain:w300

基本的な事項のおさらいをした後に、本題の証明を紹介したいと思います。

整域とは

まず、可換環 $R$ を考えます。可換環は要するに「足し算・引き算・掛け算ができ、掛け算が可換な集合」のことですが、詳しい定義は何かしらの教科書をご覧ください。

一つだけ注意すると、一般に「可換環」といったときに「単位元 $1$ を持つ流儀」と「持たないものも含む流儀」があるのですが、ここでは可換環といったら単位元を持つこととします。

もし、 $R$ の 0 でない元 $a, b \in R$ で、 $ab = 0$ となるようなものが存在するとき、 $R$ は零因子を持つといいます。零因子を持たない可換環のことを整域といいます。

ここから先は整域のみを考えます。零因子を持つといろいろややこしくなるので、できれば持ってほしくないわけですね。

当然ですが、有理整数環 $\mathbb{Z}$ は零因子を持たないので整域です。

ユークリッド整域（ED）とは

続いて、ユークリッド整域の定義を確認しましょう。ユークリッド整域は、英語でEuclidean Domainなので、EDと略すことが多いです。

定義は以下の通りです。

定義（ユークリッド整域）

$R$ を整域とし、写像 $\phi\colon R\setminus \{0\} \to \mathbb{N}$ を考える。 $(R, \phi)$ が次の条件を満たすとき、 $R$ は $\phi$ を備えたユークリッド整域であるといい、 $\phi$ をユークリッド関数という。

$R$ の 0 でない任意の元 $a$ と任意の元 $b$ に対して、ある $R$ の元 $q, r$ が一意的に存在して次を満たす：

$b = aq + r, \;\; r = 0$ または $\phi(r) < \phi(a)$

要するに、 $b$ を $a$ で割った「商 $q$ 」と「あまり $r$ 」が一意的に定まるような整域ということです。

もちろん、単に $b = aq + r$ となるような $q, r$ というだけだったら、どんな整域でもとることができます。（たとえば、 $q = 0, \; r = b$ とすればよいでしょう。）

そこで何らかの制約をつける必要があるわけですが、それが「 $r = 0$ または $\phi(r) < \phi(a)$ 」なわけですね。この制約のお気持ちとしては、 $b$ を $a$ で割っているので、そのあまり $r$ としては $a$ より「小さく」なってほしいというものです。

一般の $R$ には順序が入っているとは限りませんので、ユークリッド関数 $\phi$ を用意して、 $R$ の 0 でない元を $\mathbb{N}$ に対応づけます。自然数 $\mathbb{N}$ には、全順序が入っているので、 $a$ と $r$ の「大きさ」が比較できるというわけですね。

なお、この記事では自然数 $\mathbb{N}$ として $0 \not \in \mathbb{N}$ であるものを考えています。

有理整数環 $\mathbb{Z}$ はユークリッド整域の例の一つです。絶対値をとる関数 $|\cdot| \colon \mathbb{Z}\setminus 0 \to \mathbb{N}$ を考えると、有理整数環 $\mathbb{Z}$ はユークリッド関数 $|\cdot |$ を備えたユークリッド整域です。

実際、任意の $a \neq 0, b \in \mathbb{Z}$ に対して、

$b = aq + r, \;\; r = 0$ または $|r| < |a|$

が成り立つのですが、証明はぜひ自分で考えてみてください。
（わからないという人は、参考文献の1.3節で）

単項イデアル整域（PID）とは

最後に、単項イデアル整域の定義を確認しましょう。単項イデアル整域は、英語でPrincipal Ideal Domainなので、PIDと略すことが多いです。

PIDより先に、まずイデアルの定義をしておきましょう。

定義（イデアル）

$R$ を可換環とする。 $R$ の空でない部分集合 $A$ が以下の 1, 2 を満たすとき、 $A$ は $R$ のイデアルであるという。

任意の $a, b \in A$ に対し、 $a - b \in A$
任意の $a \in A$ と任意の $r \in R$ に対し $ar \in A$

※空でないという部分は大変重要なのですが、忘れがちなので注意。

たとえば、 $a, b \in R$ に対して

$A = aR + bR \;\; \left(= \{ax+by \; \middle| \; x, y \in R \} \right)$

という形の集合もイデアルですし、 $c \in R$ に対し

$A = cR \;\; \left(= \{cz \; \middle| \; z \in R \} \right)$

という形の集合もイデアルです。特に後者のイデアルは、1つの元により生成されるイデアルなので、単項イデアルといいます。

イデアルはなかなか難しい概念ですよね。イメージが湧かない人もいるかと思いますが、こちらの記事はそういう人の助けになるものかと思います。よければご覧ください。

tsujimotter.hatenablog.com

さて、このように準備すると、単項イデアル整域は次のように定義されます。

定義（単項イデアル整域）

$R$ を整域とする。 $R$ が次の条件を満たすとき、 $R$ は単項イデアル整域であるという。

$R$ の任意のイデアル $A$ は単項イデアルである。すなわち、 $R$ の任意のイデアル $A$ に対して、 $m\in R$ が存在して $A = mR$ が成り立つ。

これで準備は整いました。

ED => PID の証明（本題）

それでは本題に入ります。ユークリッド整域ならば単項イデアル整域であることを証明しましょう。

示したい定理は次のものです。

定理１（ $\text{(ED)}\Longrightarrow \text{(PID)}$ ）

$R$ を整域とする。このとき、次が成り立つ：

$R$ はユークリッド関数 $\phi\colon R\setminus \{0\} \to \mathbb{N}$ を備えたユークリッド整域
$\Longrightarrow \;\;$ $R$ は単項イデアル整域

（証明）
$A \subset R$ を $R$ の任意のイデアルとする。ここで、イデアルの性質 1 より、 $0 \in A$ である。

イデアル $A$ は空でないので $x \in A$ が取れます。
イデアルの性質 1 を $b = a = x$ として適用すると、 $x - x = \in A$ が言えますが、 $x - x = 0$ なので $0 \in A$ となります。

(i) $A = \{0\}$ のとき：
$m = 0$ として、 $A = mR$ が成り立つ。

(ii) $A \neq \{0\}$ のとき：
$0$ ではない $A$ の元をとることができる。特に $0$ ではない元 $m \in A$ を $\phi(m)$ が最小となるようにとる。

ここが最大のポイントです。 $R$ はユークリッド関数 $\phi$ を備えたユークリッド整域であることを仮定しています。ユークリッド関数は 0 でない元に対して、自然数の値を対応づけるので、 $\phi(m)$ には順序が入るわけです。この順序に基づいて、最小の元を一つとれるということです。

$R$ はユークリッド整域より、任意の $a \in A$ に対して

$a = mq + r, \;\; r = 0$ または $\phi(r) < \phi(m)$

なる $q, r \in R$ が一意的に存在する。

$a \in A, \; mq \in A$ より、 $r = a - mq \in A$ である。

$mq \in A$ はイデアルの性質 2 より言えます。また、 $a - mq \in A$ もイデアルの性質 1 から言えます。

ここでもし $r \neq 0$ であるとすると、 $\phi(r) < \phi(m)$ であるが、これは $\phi(m)$ の最小性に反する。

よって $r = 0$ であるから、任意の $a \in A$ に対して $q\in R$ が存在して $a = mq$ が成り立つことが言えた。すなわち、 $A \subset mR$ である。

逆に、 $m \in A$ より、任意の $q \in R$ に対して $mq \in A$ である。

ここでもイデアルの性質 2 を使っています。

よって、 $mR \subset A$ である。

以上の議論により、 $A \subset mR$ かつ $mR \subset A$ が言えたので、 $A = mR$ が成り立つことが示された。

$A \subset B$ かつ $B\subset A$ ならば $A = B$ というのは、集合のイコールを示す際の定番の方法ですね。

（証明終わり）

具体例： $R = \mathbb{Z}$ の場合とベズーの等式

ここまで抽象的なユークリッド整域で議論してきましたが、せっかくなので $R$ に具体的な環を入れて確認してみましょう。

$R = \mathbb{Z}$ とします。上で述べたように、 $\mathbb{Z}$ はユークリッド関数 $|\cdot|$ を備えたユークリッド整域です。

上の $\text{(ED)} \Longrightarrow \text{(PID)}$ の証明により、任意の $\mathbb{Z}$ のイデアル $A$ は、整数 $m$ が存在して $A = m\mathbb{Z}$ と表すことができます。

すなわち、 $\mathbb{Z}$ は単項イデアル整域であるということですね。

特に、 $a, b \in \mathbb{Z}$ として、 $A = a\mathbb{Z} + b\mathbb{Z}$ なるイデアルを考えると

$a\mathbb{Z} + b\mathbb{Z} = m\mathbb{Z}$

なる等式が得られます。ここから少し議論を加えると以下の定理が導かれます。

定理２（ベズーの等式）

$a, b, c \in \mathbb{Z}$ とする。このとき、 $x, y \in\mathbb{Z}$ が存在して

$ax + by = c$

が成り立つためには、 $\operatorname{GCD}(a, b) \mid c$ であることが必要十分条件である。

すなわち、イデアルの等式 $a\mathbb{Z} + b\mathbb{Z} = m\mathbb{Z}$ における $m$ が、具体的に $\operatorname{GCD}(a, b)$ としてとれるという主張です。

証明は以下の通りです。

（定理２の証明） $A = a\mathbb{Z} + b\mathbb{Z}$ 、 $d = \operatorname{GCD}(a, b)$ のとき、 $A = d\mathbb{Z}$ を示す。

任意の $A$ の元 $z$ を $z = ax + by$ とおく（ $x, y \in \mathbb{Z}$ ）。 $d$ は $a, b$ の公約数より $a = da', \; b = db'$ とおくと（ $a', b' \in \mathbb{Z}$ ）、

$ax + by = d(a'x + b'y) \in d\mathbb{Z}$

である。よって、 $z \in A$ ならば $z \in d\mathbb{Z}$ がいえたので、 $A \subset d\mathbb{Z}$ である。

$\mathbb{Z}$ はPIDなので、任意の $\mathbb{Z}$ のイデアルは整数 $m > 0$ が存在して $A = m\mathbb{Z}$ とかけるから、 $m\mathbb{Z} \subset d\mathbb{Z}$ が言える。特に、 $d \mid m$ である。

一方、 $a, b \in A = m\mathbb{Z}$ であるから、 $m$ は $a, b$ の公約数である。最大公約数 $d$ の定義により、 $m \leq d$ である。

したがって、 $d \mid m > 0$ かつ $m \leq d$ より、 $m = d$ である。したがって、 $A = d\mathbb{Z}$ を示せた。

おわりに

今回は「ユークリッド整域（ED）」ならば「単項イデアル整域（PID）」を一般的に証明しました。すなわち、 $(R, \phi)$ がEDであることを用いて、 $R$ がPIDであること、すなわち、任意のイデアル $A$ に対して

$A = mR$

なる $m\in R$ の存在を示しました。また、具体的に $R = \mathbb{Z}$ として、 $\mathbb{Z}$ がPIDであることも示しました。

図に表すとこんな関係になります。

証明を振り返ると、 $m$ として「 $A$ の元の中で $\phi(m)$ が最小になるもの」が具体的にとれるというのが、最大のポイントでした。 $R$ はEDなので、イデアルの任意の元 $a$ を $m$ で割ることができて、 $m$ の最小性から $a$ は $m$ の倍数になってしまう、つまりPIDであったというわけですね。

なかなか面白い証明でした。

最後まで読んでくださりありがとうございました。参考文献は以下の本です。

素数と2次体の整数論 (数学のかんどころ 15)