群コホモロジーの定義と低次のコホモロジー

今回のテーマは「群コホモロジー」です。

整数論や諸々を勉強していると、群コホモロジーという言葉をよく耳にします。調べてみると、とても難しそうな定義が並んでいてよくわからない。少し前までの私はそんな感じでした。

一方で、難しい定義であっても、辛抱強く理解しようと試みれば、いつの間にか慣れてしまうこともあるようです。実際、今の私はそれなりに群コホモロジーを受け入れることができています。

まずは定義を受け入れてみることが大事なのかもしれません。というわけで、「定義をとにかく理解する」を目標に、群コホモロジーの定義について、私の理解できた範囲でまとめてみたいと思います。

記事の後半では、具体的な計算とともに「ヒルベルトの定理90」という重要な定理についても紹介します。

よくわかっている人向けの注釈：

群コホモロジーの定義は、①コチェイン複体を用いた方法と②導来関手を用いた方法がありますが、今回は簡単のため①の方法で定義を紹介したいと思います。

複体

$G$ を群とします。また、 $M$ を $G$ が作用する加群（ $G$ -加群）とします。 $G$ -加群の定義は次の通りです：

定義（ $G$ -加群）

群 $G$ が加群 $M$ に作用するとは、 $M$ の任意の元 $x$ と $G$ の任意の元 $g$ に対して、 $gx$ という $M$ の元が定まり、次の1, 2, 3が成り立つことを言います：

任意の $g, h \in G$ と $x \in M$ に対し $(gh)x = g(hx)$
$G$ の単位元 $e$ と任意の $x \in M$ に対し $ex = x$
任意の $g \in G$ と $x, y \in M$ に対し $g(x+y) = gx + gy$

このとき、 $M$ は $G$ -加群であるという。

1, 2 が成り立つとき、 $G$ は集合 $M$ に作用するといいます。1 は一見「当たり前」の条件に見えますが、 $gh$ は群 $G$ における演算で、 $hx$ は $M$ の元への作用を表します。違う世界の演算同士が可換であるというのがポイントです。

加えて、今回は特に「 $M$ は加群」としているので、 $M$ の演算 $+$ の構造を保つという条件 3 が入っています。

群作用の典型的な例としては、 $K$ 上のガロア拡大 $L$ の乗法群 $L^\times$ とガロア群 $G = \operatorname{Gal}(L/K)$ があります。 $G$ の元 $\sigma$ は $L^\times$ の元に作用しますね。

このような $G, M$ の組に対して、以下のような集合を考えます。

$C^n(G, M) := \{ \varphi \colon G^n \to M \}$

$G$ の元 $n$ 個組 $(g_1, g_2, \ldots, g_n)$ に対して $M$ の元を1つ割り当てる写像 $\varphi$ 全体を考えるわけですね。

注意したいのは、この写像というのは本当に単なる写像であって、何か構造を保存したりする必要は一切ないということです。

また、この $C^n(G, M)$ はアーベル群の構造を持つことに注意しましょう。 $\varphi_1, \varphi_2 \in C^n(G, M)$ の間の加法 $\varphi_1 + \varphi_2$ を次のように定めます。

$(\varphi_1 + \varphi_2)(g_1, \ldots, g_n) := \varphi_1(g_1, \ldots, g_n) + \varphi_2(g_1, \ldots, g_n)$

行き先の $M$ にはアーベル群の構造が入っていましたので、右辺の $+$ は $M$ における加法です。こうしてあげれば、 $\varphi_1 + \varphi_2$ という $G^n$ から $M$ への写像がきちんと定まりますね。

さて、次が一番難しいのですが、 $C^n(G, M)$ と $C^{n+1}(G, M)$ の間には、次の $d^{n+1}$ という写像が定まります。定義は次の通りです。

定義

$n \geq 0$ に対して

$d^{n+1}\colon C^n(G, M) \longrightarrow C^{n+1}(G, M), \;\; \varphi \longmapsto d^{n+1}(\varphi)$

を次の式で定義する：

$\begin{align} d^{n+1}(\varphi)(g_1, \ldots, g_{n+1}) := \; &g_1 \varphi(g_2, \ldots, g_{n+1}) \\ &+ \sum_{i=1}^{n} (-1)^i \varphi(g_1, \ldots, g_{i-1}, g_{i}g_{i+1}, g_{i+2}, \ldots, g_{n+1} ) \\ &+ (-1)^{n+1}\varphi(g_1, \ldots, g_n) \end{align} \tag{1}$

「なんだこりゃ」と思った人も多いかと思います。実際、私も「難しすぎてこんなのわかるわけない」と思っていました。この写像をとにかく理解しないと、群コホモロジーの定義が理解できないというのだから大変です。

というわけで、冒頭で述べた通り「定義をとにかく理解する」を目標に、なんとか理解を試みましょう。以下の枠内で、可能な限り丁寧に、この写像 $d^{n+1}(\varphi)$ の定義について説明したいと思います。

まずは $d^{n+1}$ がどんな写像かについて理解しましょう。

$d^{n+1}$ の定義

$d^{n+1}\colon C^n(G, M) \longrightarrow C^{n+1}(G, M), \;\; \varphi \longmapsto d^{n+1}(\varphi)$

を観察します。 $d^{n+1}$ によって、「 $n$ 個の $G$ の元をとる $\varphi$ という写像」が「 $n+1$ 個の元をとる $d^{n+1}(\varphi)$ という写像」に対応するわけですね。

「写像 $\varphi$ から写像 $d^{n+1}(\varphi)$ に対応する写像 $d^{n+1}$ 」というように、写像が入れ子になっているのがややこしいですね。

$d^{n+1}(\varphi)$ というのが行き先の写像の名前です。 $d^{n+1}(\varphi)$ は、 $g_1, \ldots, g_{n+1}$ という引数を受け取り $d^{n+1}(\varphi)(g_1, \ldots, g_{n+1})$ なる $M$ の元に対応する写像であるというわけですね。

というわけで、あとは $d^{n+1}(\varphi)(g_1, \ldots, g_{n+1})$ の定義式 $(1)$ が分かれば良いですね。式 $(1)$ の両辺の変数の個数に着目しましょう。

左辺の変数は $g_1, \ldots, g_{n+1}$ の $n+1$ 個です。一方、 $d^{n+1}(\varphi)$ を作る「素」となる $\varphi$ は変数が $n$ 個しかありません。一個足りないのです。

一方、右辺には3つの項があります。複雑ですが、順番に確認しましょう。

右辺第1項目は $g_1 \varphi(g_2, \ldots, g_{n+1})$ となっていますが、 $\varphi$ の変数には $g_2, \ldots, g_{n+1}$ の $n+1$ 個が入っています。なるほど、 $g_1$ だけ取り出して、残り $n$ 個を $\varphi$ に突っ込んだんですね。 $\varphi(g_2, \ldots, g_{n+1})$ の値は $M$ の元になりますから、 $g_1$ の $\varphi(g_2, \ldots, g_{n+1})$ への作用は定義されています。よって、 $g_1\varphi(g_2, \ldots, g_{n+1})$ という値は計算できますね。

右辺第2項目はシグマ記号になっていますが、その $i$ 番目の項を考えてみましょう。 $\varphi(g_1, \ldots, g_{i-1}, g_{i}g_{i+1}, g_{i+2}, \ldots, g_{n+1} )$ という形をしています。とてもややこしそうに見えますが、実はそれほど難しくはありません。先ほど述べたように $\varphi$ には変数が $n$ 個しか入りませんから、変数を一つ減らす必要があります。

まず、 $1$ 番目から $i-1$ 番目までに $g_1, \ldots, g_{i-1}$ を順に代入、

$\varphi(g_1, \ldots, g_{i-1}, \ast, \ast, \ldots, \ast)$

$i+1$ 番目から $n+1$ 番目までに $g_{i+2}, \ldots, g_{n+1}$ を順に代入、

$\varphi(g_1, \ldots, g_{i-1}, \ast, g_{i+2}, \ldots, g_{n+1})$

最後に、残った $i$ 番目には $g_i$ と $g_{i+1}$ を掛け合わせた $g_ig_{i+1}$ を代入

$\varphi(g_1, \ldots, g_{i-1}, g_ig_{i+1}, g_{i+2}, \ldots, g_{n+1})$

という具合に入れていきます。これでちょうど $n$ の枠に収まりましたね。

あとは、 $(-1)^i$ の符号をつけるというわけですが、これにより $-, +, -, +, \ldots$ の順に符号がつくことになりますね。

最後に第3項目ですが、これは単純に $g_{n+1}$ だけを除いて普通に代入しています。符号は、第2項における最後の項が $-$ であれば $+$ 、 $+$ であれば $-$ がつくようになっています。

たしかに $G^{n+1}$ から $M$ への写像 $d^{n+1}(\varphi)$ が定義できていることが確認できましたね。

もちろん、なぜこのような写像を定義するのかは、今のところさっぱりわかりません。一方で、冒頭に述べた通り今回の目的は「定義をとにかく理解する」なので、これぐらいでよしとしましょう。後半で具体的な計算をするので、そのときにはもう少し実態がつかめるかもしれません。

さて、写像 $d^{n+1} \colon C^n(G, M) \to C^{n+1}(G, M)$ ですが、良い性質が二つあります。

一つは、群準同型写像であるということです。 $C^n(G, M)$ はアーベル群であることは先ほど述べました。この構造を保つような写像になっているということで、すなわち

$d^{n+1}(\varphi + \psi) = d^{n+1}(\varphi) + d^{n+1}(\psi)$

が成り立っているということです。これは簡単に証明できるので、ぜひ自分で考えてみてください。

もう一つの性質は、 $n \geq 0$ に対して $d^{n+1} \circ d^{n} = 0$ が成り立つということです。こちらは簡単にはいかないので、ここでは省略したいと思います。

別の方の記事ですが、こちらでは実際に $d^{n+1} \circ d^{n} = 0$ の証明が解説されています：

#数学群コホモロジーは本当に2 回で零写像になるのか？ - 佐藤蓮のイラスト - pixiv

ということで、以上の議論から $C^n(G, M)$ と $d^{n}$ は次のような性質を持つことがわかりました。

命題（複体）

アーベル群の準同型の列

$C^0(G, M) \xrightarrow{d^1} C^1(G, M)\xrightarrow{d^2} C^2(G, M)\xrightarrow{d^3} \cdots$

は、 $n \geq 0$ に対して $d^{n+1}\circ d^{n} = 0$ が成り立つ。

このような性質を持つアーベル群の準同型の列のことを複体といいます。

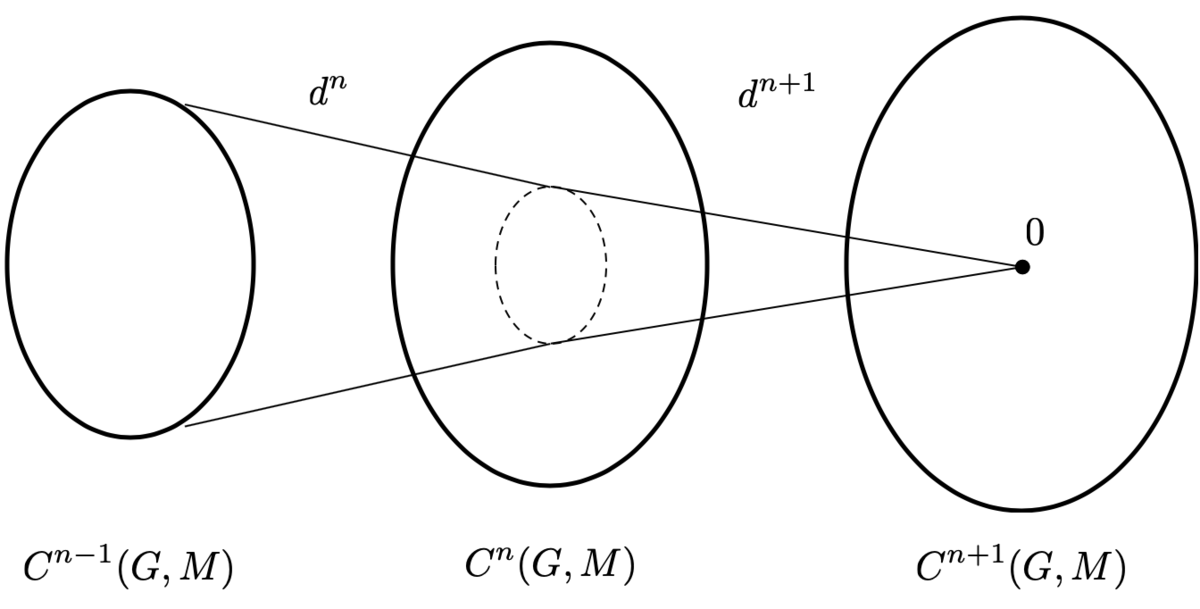
f:id:tsujimotter:20200322155240p:plain:w400

複体に対しては、次に述べる方法によって「コホモロジー」という量を計算することができます。今回の複体については、それが群コホモロジーであるというわけです。

群コホモロジーの定義

準備が整ったので、いよいよ群コホモロジーを定義しましょう。

$n$ -コサイクル $Z^n(G, M)$ という $C^n(G, M)$ の部分群を次で定義します：

$Z^n(G, M) := \operatorname{Ker}(d^{n+1})$

準同型写像 $d^{n+1} \colon C^n(G, M) \to C^{n+1}(G, M)$ に着目して、写像 $d^{n+1}$ の行き先が 0 になるような $C^n(G, M)$ の部分群を考えるわけですね。素朴には、方程式 $d^{n+1}(\varphi) = 0$ を満たす $\varphi$ 全体と考えることができます。

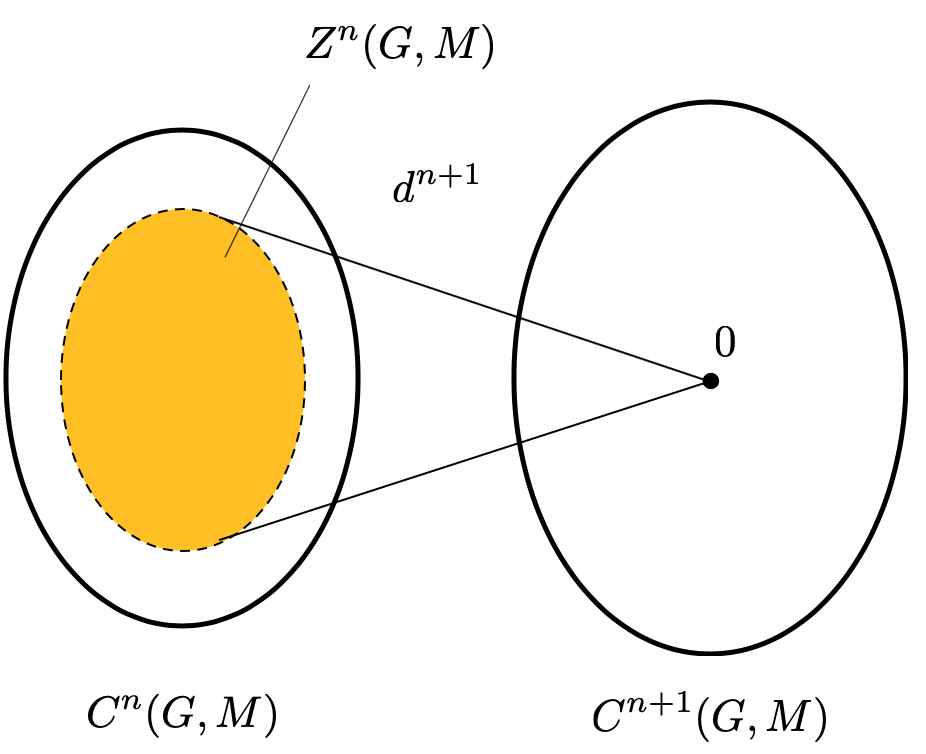
f:id:tsujimotter:20200322154931p:plain:w260

続いて、 $n$ -コバウンダリ $B^n(G, M)$ という $C^n(G, M)$ の部分群を次で定義します：

$B^n(G, M) := \operatorname{Im}(d^{n})$

今度は、1次下がった準同型写像 $d^{n} \colon C^{n-1}(G, M) \to C^{n}(G, M)$ に着目して、この像を $B^n(G, M)$ とするのですね。素朴には、1次下の写像 $\psi \in C^{n-1}(G, M)$ によって、 $\varphi = d^{n}(\psi)$ と表せる $\varphi$ 全体の集合と考えることができます。

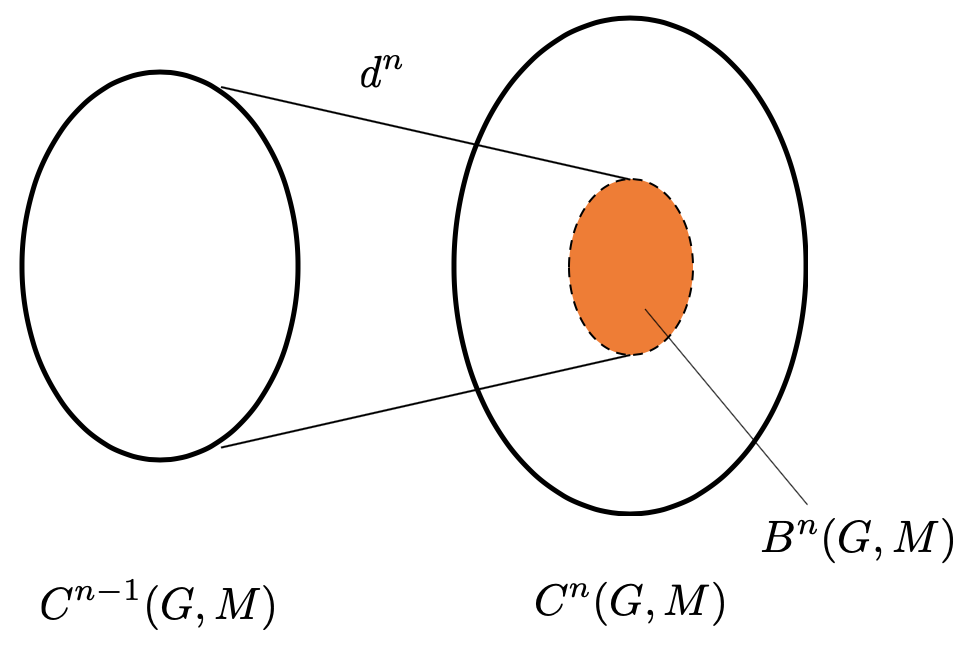
f:id:tsujimotter:20200322155002p:plain:w250

コバウンダリの定義では $d^{n}\colon C^{n-1}(G, M) \to C^n(G, M)$ が現れますが、 $n = 0$ のときは $C^{-1}(G, M)$ を計算する必要があり、そのままでは0-コバウンダリが定義できません。

そこで、 $n = 0$ のときは $B^{0}(G, M) := 0$ と定義することにします。

「 $n$ -コバウンダリは $n$ -コサイクルであること」すなわち、 $B^{n}(G, M) \subset Z^n(G, M)$ であることは、複体の条件を使って次のように示すことができます。

$\varphi$ を $n$ -コバウンダリの任意の元とします。 $n$ -コバウンダリは、 $(n-1)$ -次の写像 $\psi \in C^{n-1}(G, M)$ を使って $\varphi = d^{n}(\psi)$ と表せるのでした。これに $d^{n+1}$ を適用すると

$d^{n+1}(\varphi) = d^{n+1}( d^{n}(\psi) ) = 0$

となります。最後の等号は、複体の条件 $d^{n+1} \circ d^{n} = 0$ からしたがいます。複体の条件はここで効いてくるのですね。

よって、 $\varphi$ は $n$ -コサイクルであり、 $B^{n}(G, M) \subset Z^n(G, M)$ が言えました。

f:id:tsujimotter:20200322155048p:plain:w400

コバウンダリがコサイクルの部分群になることがわかったので（特にアーベル群の部分群より正規部分群なので）、コサイクルをコバウンダリで割った剰余群

$H^n(G, M) := Z^n(G, M)\big/ B^n(G, M)$

を考えることができます。これが $n$ 次の群コホモロジーの定義です。

もし群コホモロジー $H^n(G, M)$ が 0 になるとき、すなわち

$\operatorname{Ker}(d^{n+1}) = \operatorname{Im}(d^{n})$

が成立するとき、上記の複体は $C^n(G, M)$ において完全であるといいます。

コホモロジーは「完全からどれだけ離れているか」を表す量になっているというわけですね。

低次のコホモロジーの計算

せっかく群コホモロジーを定義したので、 $n = 0, 1$ について、具体的に計算してみましょう。

$H^0(G, M)$ の計算：

$n = 0$ のとき、 $\varphi\in C^0(G, M)$ を考えたいと思います。ここは少し特殊ですが、1元集合 $\{\ast\}$ から $M$ への写像を考えることになります。
（空集合を添字集合とする直積集合を考える必要があります。）

上の結果を受け入れて $C^0(G, M)$ を「1元集合 $\{\ast\}$ から $M$ への写像全体」だと思うと、 $C^0(G, M)$ の任意の写像 $\varphi$ は行き先の値によって決まります。したがって、 $C^0(G, M) = M$ ということになります。

0-コサイクルは、 $Z^0(G, M) = \operatorname{Ker}(d^1)$ なので、 $d^1$ を計算します。 $\varphi \in C^0(G, M)$ とすると、 $d^{1}(\varphi) \in C^1(G, M)$ は

$d^{1}(\varphi)(g_1) = g_1 \varphi(\ast) - \varphi(\ast)$

となります。 $\varphi$ は1元集合からの写像なので、 $\varphi$ の引数には $\ast$ しか入らないことに注意します。

$C^0(G, M) = M$ なので、 $M$ の元だと思って $x := \varphi(\ast) \in M$ と書き直すと

$d^{1}(x)(g) = g x - x$

となります。0-コサイクルは $d^{1}(x) = 0$ となるような $x \in M$ のことですから、任意の $g$ に対して $gx = x$ を満たす $x \in M$ ということになります。これは、 $G$ によって固定される $M$ の部分群 $M^G$ のことですね。

というわけで、 $Z^0(G, M) = M^G$ であることがわかりました。

また0-コバウンダリは、上で注意したように $B^0(G, M) = 0$ と定義されますので、0次の群コホモロジーは

$H^0(G, M) = Z^0(G, M) = M^G$

ということになります。

たしかに、 $G$ の $M$ への作用に関する情報を取り出している感じがしますね。

$H^1(G, M)$ の計算：

続いて、 $n = 1$ のときを考えましょう。

まず、 $C^1(G, M)$ は $G$ から $M$ への写像全体です。これはそのまま考えて良いでしょう。あえていうなら、 $C^1(G, M) = \operatorname{Map}(G, M)$ ですね。

$n = 0$ のときとは順番が逆になりますが、1-コバウンダリから計算します。このためには $d^1$ を計算する必要がありますが、これは $H^0$ のときに計算していましたね。

$d^{1}(x)(g) = g x - x$

1-コバウンダリは、 $B^1(G, M) = \operatorname{Im}(d^1)$ でした。よって、 $\varphi \in B^1(G, M)$ は、 $x\in M$ が存在して、任意の $g \in G$ に対して

$\varphi(g) = g x - x$

となるような $\varphi \colon G \to M$ ということになります。 $\varphi(g)$ の値が「 $x$ という数への作用を通して具体的にかける」という特徴を持った $\varphi$ ということですね。

最後に、1-コサイクルを計算します。このためには今度は $d^2$ を計算する必要があります。再度、 $\varphi \in C^1(G, M)$ とし、 $d^2(\varphi) \in C^2(G, M)$ を定義に従って計算すると

$d^{2}(\varphi)(g_1, g_2) = g_1 \varphi(g_2) - \varphi(g_1 g_2 ) + \varphi(g_1)$

となります。だんだん慣れてきたでしょうか？

したがって、1-コサイクルは $Z^1(G, M) = \operatorname{Ker}(d^2)$ より、 $d^{2}(\varphi) = 0$ 。すなわち、任意の $g_1, g_2 \in G$ に対して

$g_1 \varphi(g_2) - \varphi(g_1 g_2 ) + \varphi(g_1) = 0$

を満たす $\varphi \colon G \to M$ 全体ということになります。

移項して少しだけ整理すると

$\varphi(g_1 g_2) = \varphi(g_1) + g_1 \varphi(g_2)$

ということになるでしょうか。

どうやって理解するかは人それぞれですが、私個人的には、これは「少し崩れた準同型性」に見えます。普通の意味での準同型性というと

$\varphi(g_1 g_2) = \varphi(g_1) + \varphi(g_2)$

のようになると思うのですが、これはそのまま成り立たなくて $\varphi(g_2)$ に $g_1$ の作用がくっついたような「少し崩れた」ものを1-コサイクルと呼ぶということですね。

以上により、1次の群コホモロジーは次のようになります。

$\displaystyle H^1(G, M) = \frac{\{ \varphi \in C^1(G, M) \mid \varphi(g_1 g_2) = \varphi(g_1) + g_1 \varphi(g_2) \; \text{for all} \; g_1, g_2 \in G \}}{\{ \varphi \in C^1(G, M) \mid \exists x \in M \; \text{s.t.} \; \varphi(g) = gx - x \; \text{for all} \; g \in G\}}$

よりイメージが湧くように、少し特殊な状況で1次の群コホモロジーを考えたいと思います。 $G$ が $M$ に自明に作用している状況です。「 $G$ が $M$ に自明に作用する」とは、任意の $g \in G, \; x \in M$ に対して $gx = x$ が成り立つということです。

この状況下では、1-コサイクル $\varphi$ は

$\varphi(g_1 g_2) = \varphi(g_1) + \varphi(g_2)$

となります。これはつまり、 $\varphi$ は群準同型写像ということです。

また、1-コバウンダリを考えると $\varphi(g) = gx - x = 0$ より、任意の1-コバウンダリは $\varphi(g) = 0$ となります。

したがって、1次の群コホモロジーは次のように表すことができるでしょう。

命題

$G$ が $M$ に自明に作用するとき、1次の群コホモロジーは次のように表せる：

$H^1(G, M) = \operatorname{Hom}(G, M)$

ただし、 $\operatorname{Hom}(G, M)$ は $G$ から $M$ への群準同型写像全体のなすアーベル群である。

乗法形と加法形

さて、これまで $M$ として「加法的な」演算の入った群を考えてきました。すなわち、 $x+y \in M$ というような演算が入っているということですね。

しかしながら、アーベル群だったとしても「乗法的な」演算の入った群を考えることもあるはずです。たとえば、冒頭に述べたような $L^\times$ では、乗法の演算は $xy \in L^\times$ のように表します。

群の作用についても、加法的な定義では $gx$ のように表していましたが、乗法的な定義においては $x^g$ のように表すことが多いかと思います。また、単位元も 0 から 1 に変わります。

上の群コホモロジーの定義においては、加法的な記号を使ったために、乗法的な群の場合はその都度読み替える必要が出てきます。これは非常に面倒なので、再度コサイクルやコバウンダリの計算結果を乗法的なものに表し直したいと思います。

乗法的な群ということで、 $M$ を $M^\times$ という群に書き換えてみます。（これは気分の問題です）

$n = 0$ のとき：

0-コサイクル $Z^0(G, M^\times)$ は、任意の $g \in G$ に対して $x^g = x$ となるような $x \in M^\times$ 全体となります。

0-コバウンダリは $B^0(G, M^\times) = 1$ となります。

したがって、0次コホモロジー $H^0(G, M^\times)$ は0-コサイクルに一致します。

$n = 1$ のとき：

1-コバウンダリ $\varphi \in B^1(G, M^\times)$ は、 $x \in M^\times$ が存在して、任意の $g \in G$ に対して

$\displaystyle \varphi(g) = \frac{x^g}{x}$

となるような $\varphi \colon G \to M^\times$ 全体ということになります。（「マイナス」が「割り算」に変わる点に注意ですね。）

1-コサイクル $Z^1(G, M^\times)$ は、任意の $g_1, g_2 \in G$ に対して

$\varphi(g_2)^{g_1} \varphi(g_1 g_2)^{-1} \varphi(g_1) = 1$

を満たす $\varphi \colon G \to M^\times$ 全体ということになります。

書き換えると

$\varphi(g_1 g_2 ) = \varphi(g_1) \varphi(g_2)^{g_1}$

を満たす $\varphi$ ということになりますね。

ヒルベルトの定理90

最後に、低次の群コホモロジーを考える上で、一つの重要な定理である「ヒルベルトの定理90」について紹介したいと思います。

ここまで丁寧に準備してきたので、ヒルベルトの定理90の主張は直ちに理解できます。

定理（ヒルベルトの定理90）

$K$ を体、 $L/K$ を有限次ガロア拡大とし、そのガロア群を $G := \operatorname{Gal}(L/K)$ とする。 $L$ の加法群をそのまま $L$ 、乗法群を $L^\times$ とするとき、次が成り立つ：

$H^1(G, L) = 0$

$H^1(G, L^\times) = 1$

つまり、ガロア群 $G$ は $L$ や $L^\times$ に作用するわけですが、このときの1次の群コホモロジーは消えてしまうということを主張しています。群コホモロジーが消えるという条件は、実際色々な証明に使われています。

ここでは、群コホモロジーの応用については触れませんが、定義を遡って、素朴な意味で「群コホモロジーが消える」ことの意味を確認してみましょう。

乗法群の方で確認してみましょう。

まず、ガロア群の元を $\sigma \in G$ の記号で表すことにします。また、 $C^1(G, L^\times)$ の元、すなわち写像 $x\colon G \to L^\times$ による $\sigma$ の行き先を $x_\sigma$ と表すことにします。
（ $\sigma$ に対して値 $x_\sigma$ が決まるという意味ですね。）