2017を二つの平方数の和で表す方法 (1) - tsujimotterのノートブック

この記事は数学とコンピュータ Advent Calendar 2017 の 7 日目の記事です。

数学好きなITエンジニアの皆様こんにちは。

日曜数学者を名乗り、趣味で数学を学んでいるtsujimotterと申します。本業では情報系の研究者をしていて、日頃プログラミングには親しんでいます。

私は常々、数学という学問、特に整数論を学ぶにあたってプログラミングという道具は役に立つと考えているのですが、今日はその一端を垣間見せてくれる整数論のトピックをご紹介します。

今回の目標は、 $p$ を奇数の素数としたとき

「 $p = X^2 + Y^2$ なる整数 $X, Y$ を具体的に計算する方法」

を解説することです。

今回紹介するプログラムの言語としては Ruby を用いることにします。

４で割って１あまる素数の法則

2017年は、2011年以来6年ぶりの素数の年で

$2017 = 4 \cdot 504 + 1$

より「４で割って１あまる素数」の年でもあります。

「４で割ったあまり」に着目するのには理由があります。以下の非常に有名な定理があるからです。

定理：フェルマーの二平方定理

$p$ を奇数の素数とする．このとき，以下が成り立つ：

　　整数 $n$ が存在して $p = 4n + 1$ とかける
　　　 $\Longrightarrow$ 　 $p = X^2 + Y^2$ なる整数 $X, Y$ が存在する

※この定理は「逆」も成り立ちますが、今回は使わないので解説しません。

任意の「４で割って１あまる素数」は「２つの平方数の和」で書き表すことができる、というのがこの定理の主張です。

具体的に例を計算してみると以下のようになります。

例：

$\begin{align} 5 &= 2^2 + 1^2 \\ 13 &= 3^2 + 2^2 \\ 17 &= 4^2 + 1^2 \\ 29 &= 5^2 + 2^2 \end{align}$

左辺はすべて「４で割って１あまる素数」ですから、例を見る限り、確かに成り立っていることがわかりますね。

2017 も「４で割って１あまる素数」なので、２つの平方数の和で表す方法が存在します。このような方法を具体的に考えたいわけです。

ところでフェルマーの二平方定理に関しては、以前にも本ブログで解説したことがありました。

参考：
tsujimotter.hatenablog.com

今回は、以前とは異なる方法で二平方定理の別証明を与えたいと思います。

「あれ？今回の目標は $X, Y$ を求めることじゃなかったっけ？」
と思うかもしれませんが、別証明を与えること自体は回り道にはなりません。

なぜ証明を追いかける必要があるかというと、実は今回紹介する別証明が、 $X, Y$ を求めるための具体的なアルゴリズムを提供してくれるからです。

すなわち、 $X, Y$ の存在を示す証明が、そのまま $X, Y$ を計算するアルゴリズムになっているというわけですね。このような証明を「構成的」な証明というそうです。一方で、以前紹介した証明法は「鳩ノ巣原理」を用いる「非構成的」な証明となっており、具体的な計算のためには（直接は）役に立ちません。

方針

$p = 4n+1$ から、直接 $p = X^2 + Y^2$ が導けるわけではありません。定理の証明のためには、一旦以下の命題を経由する必要があります。

命題1

$p$ を奇数の素数とする．このとき，以下が成り立つ：

　　整数 $n$ が存在して $p = 4n + 1$ とかける
　　　 $\Longrightarrow \;\; X^2 \equiv -1 \pmod{p}$ なる整数 $X$ が存在する

$X^2 \equiv a \pmod{p}$ となる整数 $X$ が存在するような $a$ を、法 $p$ の 平方剰余 といいます。

平方剰余という言葉を用いると、この命題の主張は「 $p = 4n+1$ ならば $(-1)$ は法 $p$ の平方剰余である」と言い換えられます。この命題は、平方剰余の背後にある非常に美しい法則の一端となっています。

興味がある方は「平方剰余の相互法則」や「平方剰余の第一補充則」のような言葉で調べると良いかと思います。

なかなか奥深い命題なので、ここで証明することはしませんが、この命題が成り立つことを受け入れて話を進めたいと思います。

命題1を受け入れると、「フェルマーの二平方定理」を示すためには、以下を証明すればよいことがわかります。

命題2

$p$ を奇数の素数とする．このとき，以下が成り立つ：

　　 $X^2 \equiv -1 \pmod{p}$ なる整数 $X$ が存在する
　　　 $\Longrightarrow$ 　 $p = X^2 + Y^2$ なる整数 $X, Y$ が存在する

話の流れを整理しましょう。これまで、図のような流れで議論を進めてきました。

f:id:tsujimotter:20171206211116p:plain:w480

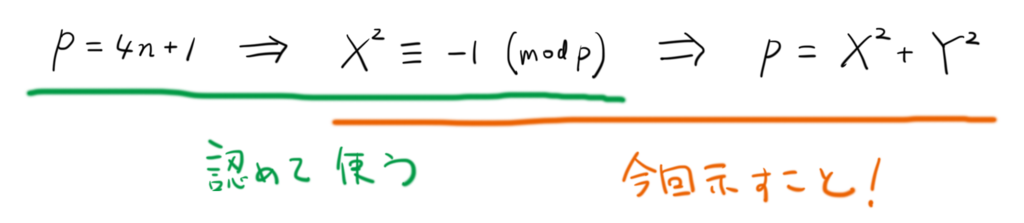
以下では、図の右側の矢印（命題2）の証明に注力したいと思います。

２つのキーポイント

ここでは、証明のキーになる２つの道具を紹介しましょう。

まずは、ブラーマグプタの恒等式 です。

ブラーマグプタの恒等式

$(a^2+b^2)(z^2+w^2)=(az+bw)^2+(aw−bz)^2$

高校生でも習うような簡単な恒等式ですが、私は「ブラーマグプタの恒等式」が、この世に存在する恒等式の中でもっとも好きです。

式を解釈すると、左辺は２組の「２つの平方数の和」の間の積となっています。右辺は「２つの平方数の和」となっています。したがって、この恒等式は「２つの平方数の和全体の集合が積に対して閉じている」ということを主張しています。

f:id:tsujimotter:20171206213417p:plain:w320

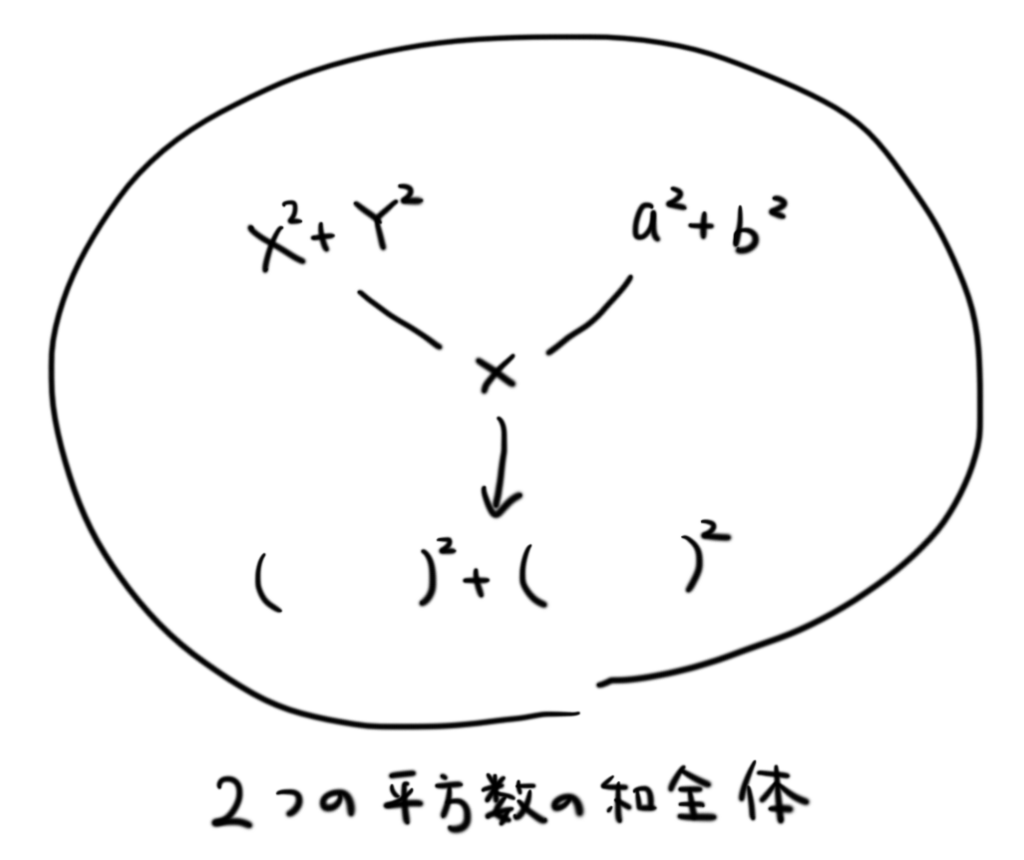
ブラーマグプタの恒等式は今回の証明の重要なパートを担います。Wikipediaによると

この恒等式はディオファントスによって発見され、インドの数学者・天文学者であるブラーマグプタ（598年 - 668年）によって再発見された。

とあります。大昔から知られていた恒等式が、近代的な数論の証明に役に立つというのは面白いですね。

もう一つのキーポイントは、無限降下法です。無限降下法は、以下のような論法です。

「条件A」を満たす都合のよい自然数 $k > 1$ が与えられたとき、 $k$ から「条件A」と $k > k'$ を満たす自然数 $k'$ を作れるとします。すると、 $k' > 1$ であれば同様に $k'$ を使って $k' > k''$ を満たす $k''$ を作ることができます。

f:id:tsujimotter:20171206213117p:plain:w400

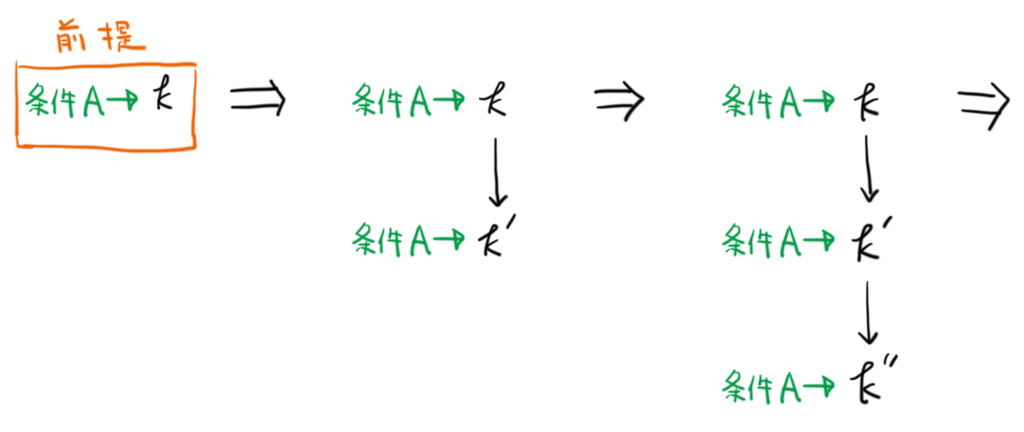
この施行は、新しく出来た $k$ が $1$ になるまでいくらでも続けられ、有限回の繰り返しで $1$ に到達します。したがって「条件A」をみたす $k > 1$ が一つでも存在すれば、 $k = 1$ は「条件A」を満たすことがわかるというものです。

f:id:tsujimotter:20171206213159p:plain:w250

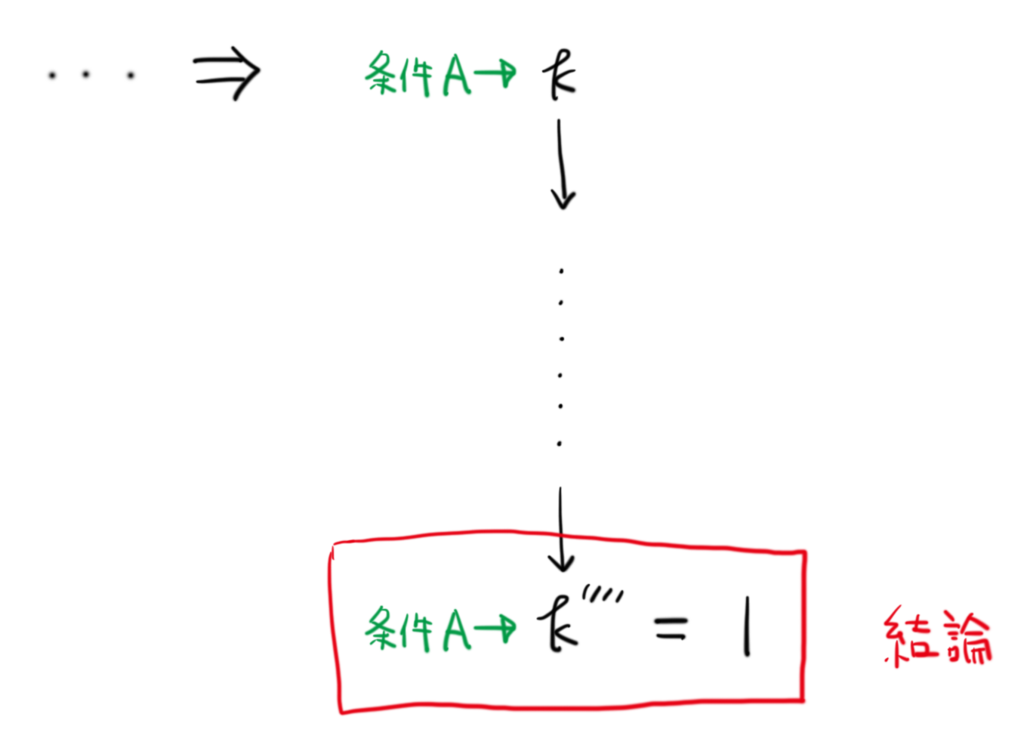
自然数の範囲で下に降下していけば、いつかは $1$ にたどり着く、という「自然数の強い性質」を利用した証明法です。フェルマーが多用したので、フェルマーの無限降下法と呼ばれることもあるそうです。

二平方定理の別証明

それでは、以上の道具を使って

「 $X^2 \equiv -1 \pmod{p}$ のとき $p = X^2 + Y^2$ と表せる」

を証明しましょう。

少し長いですが、以下の点線枠内が証明です。先のキーポイントを用いる箇所を太字で示しています。また、後のアルゴリズムで用いる箇所を太枠で囲っています。

（証明）
まず、 $X^2 \equiv -1 \pmod{p}$ より、

$X^2 + 1 = kp \tag{1}$

なる $X, k$ が存在することがわかります。

ここで、もし $k = 1$ であれば、 $Y = 1$ として

$p = X^2 + 1 = X^2 + Y^2$

が成り立つので、証明終了。

したがって、 $k > 1$ の場合を考えます。

式 $(1)$ において $Y = 1$ として

$kp = X^2 + Y^2 \tag{2}$

とする。

ここで、 $k$ で割ったあまりを考えて

$\begin{cases} x \equiv X \pmod{k} \\ y \equiv Y \pmod{k} \end{cases}$

なる整数 $x, y$ を、 $x, y$ の絶対値が最小になるようにとります*1。

このようにとると

$x^2 + y^2 \equiv X^2 + Y^2 = kp \equiv 0 \pmod{k}$

より

$x^2 + y^2 \equiv 0 \pmod{k}$

が成り立ちます。よって、左辺は $k$ で割ることができて、新たに $k'$ という整数を定義できます。

$\displaystyle k' = \frac{x^2 + y^2}{k}$

$k'$ は正の整数となります。また，

$\displaystyle k' k = x^2 + y^2 \tag{3}$

と変形します。

式 $(2), (3)$ を並べると

$\displaystyle \begin{align} k p &= X^2 + Y^2 \\ k' k &= x^2 + y^2 \end{align}$

ですが、両辺をかけると

$\displaystyle k' k^2 p = (X^2 + Y^2) (x^2 + y^2)$

は得られます。ここで、右辺は２組の「２つの平方数の和」の積の形になっていますので、ブラーマグプタの恒等式 が使えます。

ブラーマグプタの恒等式より

$\displaystyle \begin{align} k' k^2 p &= (X^2 + Y^2) (x^2 + y^2) \\ &= (Xx + Yy)^2 + (Xy - Yy)^2 \end{align} \tag{4}$

と「２つの平方数の和」で表せます。

右辺の各項は、以下の通り $k$ で割り切れることがわかります。

$\begin{cases} Xx + Yy \equiv X^2 + Y^2 &\equiv 0 \pmod{k} \\ Xy - Yx \equiv XY - YX &\equiv 0 \pmod{k} \end{cases}$

よって、これらを $k$ で割って新たな変数 $X', Y'$ を定義します。

$\displaystyle \begin{align} X' &= \frac{Xx + Yy}{k} \\ Y' &= \frac{Xy - Yx}{k} \end{align}$

これらを式 $(4)$ に代入すると

$\displaystyle k' p = X'^2 + Y'^2 \tag{5}$

が得られました。

以上をまとめると式 $(2)$

$k p = X^2 + Y^2$

から、式 $(5)$

$k' p = X'^2 + Y'^2$

が得られたことになります。

ここでもし $k > k'$ が成り立てば、 $k > k' > k'' > \cdots$ と次々小さい $k$ をとって $kp = X^2 + Y^2$ を成り立たせることができます。無限降下法 より、 $k$ は有限回の繰り返しで $1$ に一致しますから、

$p = X^2 + Y^2$

が成り立つことが示されます。

最後に $k > k'$ は次のように示されます。

$\displaystyle k' = \frac{x^2 + y^2}{k}$

であり、 $x, y$ の絶対値が最小の仮定より $x \leqq \frac{k}{2}, \; y \leqq \frac{k}{2}$ であるから、

$\displaystyle k' = \frac{x^2 + y^2}{k} \leqq \frac{(k/2)^2 + (k/2)^2}{k} = \frac{k}{2} < k$

よって、 $k > k'$ が得られました。

（証明終わり）

証明をプログラミングする

さて、ここからが「数学とコンピュータ Advent Calendar」的には本番です。今得られた証明を「プログラミング」の視点で見るとどうなるでしょうか。

無限降下法の証明をプログラムと見立てると、次のように考えられます。プログラムの入力は「証明の仮定として与えられるもの」です。それはすなわち

$k_0 p = X_0^2 + Y_0^2$

なる $(X_0, Y_0, k_0, p)$ の組のことです。これに対して

$(X_0, Y_0, k_0, p) \mapsto (X_1, Y_1, k_1, p) \mapsto \cdots \mapsto (X_m, Y_m, k_m, p)$

という処理を繰り返して、最終的に $k_m = 1$ に辿り着いて

$k_m p = X_m^2 + Y_m^2$

なる $(X_m, Y_m, 1, p)$ の組が出力されるというわけです。

プログラムの仕様：

入力： $k_0 p = X_0^2 + Y_0^2$ なる $(X_0, Y_0, k_0, p)$ の組
出力： $p = X_m^2 + Y_m^2$ なる $(X_m, Y_m, 1, p)$ の組

入力と出力が定まりましたので、実際に関数の大枠を作ってみましょう。以上の処理を実行する関数を "descent" （「降下法」の意）という名前をつけて定義しましょう。

$k = 1$ のときは、そのまま $(X, Y, k, p)$ を返します。そうでない場合は $(X, Y, k, p) \mapsto (X', Y', k', p)$ を計算してから、再度 descent を実行します。これを $k = 1$ になるまで続けます。

このような処理は、以下のように再帰的に書くことができます。

# 無限降下法 (descent)
def descent(x, y, k, p)
   if k == 1
      return [x, y, 1, p]
   else
      # ここに (x, y, k, p) 
      # 　　　-> (next_x, next_y, next_k, p) の計算を入れる

      # (next_x, next_y, next_k) に対して descent を再帰的に実行する
      return descent(next_x, next_y, next_k, p)
   end
end

$(X, Y, k, p) \mapsto (X', Y', k', p)$ の計算処理は、先ほどの証明で太枠で囲った箇所です。

まずは、絶対値が最小となる $\bmod{k}$ の剰余

$\begin{cases} x \equiv X \pmod{k} \\ y \equiv Y \pmod{k} \end{cases}$

を計算します。これは、次のコードで計算できるでしょう。

# x (resp. y) の mod k における絶対最小剰余 x_mod_k (resp. y_mod_k) をとる
x_mod_k = x % k
if x_mod_k > (x_mod_k - k).abs
   x_mod_k = x_mod_k - k
end
y_mod_k = y % k
if y_mod_k > (y_mod_k - k).abs
   y_mod_k = y_mod_k - k
end

次に

$\displaystyle \begin{align} k' &= \frac{x^2 + y^2}{k} \\ X' &= \frac{Xx + Yy}{k} \\ Y' &= \frac{Xy - Yx}{k} \end{align}$

の式によって、 $(X', Y', k', p)$ を計算します。

対応するコードは以下のようになります。

# (x, y, k) -> (next_x, next_y, next_k)
next_k = (x_mod_k**2 + y_mod_k**2) / k
next_x = (x * x_mod_k + y * y_mod_k) / k
next_y = (x * y_mod_k - y * x_mod_k) / k

以上をまとめると、次のような関数ができます。

# 無限降下法 (descent)
def descent(x, y, k, p)
   if k == 1
      return [x, y, 1, p]
   else
      # x (resp. y) の mod k における絶対最小剰余 x_mod_k (resp. y_mod_k) をとる
      x_mod_k = x % k
      if x_mod_k > (x_mod_k - k).abs
         x_mod_k = x_mod_k - k
      end
      y_mod_k = y % k
      if y_mod_k > (y_mod_k - k).abs
         y_mod_k = y_mod_k - k
      end

      # (x, y, k) -> (next_x, next_y, next_k)
      next_k = (x_mod_k**2 + y_mod_k**2) / k
      next_x = (x * x_mod_k + y * y_mod_k) / k
      next_y = (x * y_mod_k - y * x_mod_k) / k

      # (next_x, next_y, next_k) に対して descent を再帰的に実行する
      return descent(next_x, next_y, next_k, p)
   end
end

一見、無限に再帰を繰り返してしまいそうなあやういコードですが、ちゃんと停止することがわかります。無限降下法によって、有限回で $k = 1$ に到達し、プログラムが停止することが保証されているからです。

あとは、入力の組 $(X, 1, k, p)$ を入れてあげれば、 $p = X'^2 + Y'^2$ なる $(X', Y', 1, p)$ が出力されます。

まずは簡単のため、 $p = 13$ くらいで試してみましょう。ここで必要になるのは、 $X^2 + 1 = kp$ なる整数 $X, k$ ですね。

うまい方法が見当たらないので、手作業で探してみましょう。いろいろ探してみると $X = 5$ としたとき

$5^2 + 1 = 26$

が $p = 13$ で割り切れます。よって、 $k$ の方は $k = 26 / 13 = 2$ と得られます。

したがって、整数の組 $(X, Y, k, p) = (5, 1, 2, 13)$ を入力して実行してみましょう。

x = 5
y = 1
k = 2
p = 13

p descent(x, y, k, p)

すると、以下のように出力されるかと思います。

[3, 2, 1, 13]

よって、 $X = 3, \; Y = 2$ が得られました。実際に

$13 = 3^2 + 2^2$

が成り立ちますから、正しく動作していることがわかりますね。

プログラムの解釈が面倒なので、以下のような関数を導入します。

# 出力結果の見た目を整形
def pretty_format result
   x = result[0]
   y = result[1]
   k = result[2]
   p = result[3]

   return "   #{k} * #{p} = #{x.abs}^2 + #{y.abs}^2"
end

この関数をこのように使うと

puts pretty_format(descent(x, y, k, p))

以下のように、分かりやすく表示されるようになります。

   1 * 13 = 3^2 + 2^2

2017を二つの平方数の和で表す

さて、いろいろ準備したところで、本題の 2017 に挑戦してみましょう。

といいたいところですが、早速問題が生じます。 $p = 2017$ に対して descent 関数を呼ぶためには、 $X^2 + 1 \equiv 0 \pmod{2017}$ を満たす $X$ を見つける必要があります。これは実際なかなか大変です。

この計算をスマートにしたいと思っていたのですが、tsujimotterには方法がわかりませんでした*2。不本意ですが、愚直に全探索する方法をとりたいと思います。この全探索のせいで、本手法の計算はそれほど効率的ではなくなってしまいました。

上記の $X$ を求める以下の関数を追加します。

# 平方剰余を探索する
def qr a, p
   p.times do |x|
      if (x*x - a) % p == 0
         return x
      end
   end
end

$0$ から $p-1$ までの整数 $X$ に対して $X^2 - a$ を $p$ で割ったあまりを計算して、 $0$ に合同であればそのときの $X$ を出力という愚直な方法です。この "qr" 関数に $(-1, p)$ を入力すればよいでしょう。

この計算によって得られた $X$ を使い、 $k = (X^2 + 1)/p$ として $k$ も得られます。

実際に 2017 を計算するプログラムは、Gist の以下のページにおいておきました。以下のプログラムには、"descent" の計算途中に "puts" 出力を挟んで、途中経過を見れるようにしています。

fermat_descent.rb · GitHub

プログラムの中には、 $p = 2017$ だけでなく、 $p = 20171201$ も例として入れてあります。 $20171201$ も「４で割って１あまる素数」だったのですね。

"fermat_descent.rb" を実行すると、以下のようになります。

# 実行結果
$ ruby fermat_descent.rb
p = 2017
   26 * 2017 = 229^2 + 1^2
   1 * 2017 = 44^2 + 9^2

p = 20171201
   194917 * 20171201 = 1982854^2 + 1^2
   5821 * 20171201 = 342661^2 + 10^2
   104 * 20171201 = 45798^2 + 590^2
   25 * 20171201 = 16541^2 + 15188^2
   9 * 20171201 = 13245^2 + 2472^2
   2 * 20171201 = 5239^2 + 3591^2
   1 * 20171201 = 4415^2 + 824^2

少し時間がかかりますが、ほとんどが平方剰余の計算で、無限降下法の計算自体は高速に求まります。計算過程も見てみると、 $k$ の値が徐々に小さくなって、最終的に $k = 1$ にたどり着いていることがわかりますね。

以上により、念願の

$2017 = 44^2 + 9^2$

を計算することができました。めでたしめでたし。

ついでに

$20171201 = 4415^2 + 824^2$

もわかりました。笑

例に挙げた素数以外にも、上記プログラムを書き換えれば自由に計算できますので、ぜひ遊んでみてください。

まとめ

まとめると「フェルマーの二平方定理」の証明は、

証明の流れそのものが $X, Y$ を求めるアルゴリズム（プログラム）と解釈できる
プログラムの停止性が、証明成立の鍵となっている

ということでした。

キーになった道具は２つありました。

１つは、ブラーマグプタの恒等式です。この恒等式が「 $(X, Y, k)$ の組から $(X', Y', k')$ を求める手続き」を与えてくれました。

もう１つは、無限降下法です。無限降下法が「有限回で $k = 1$ に到達する」という「プログラムの停止性」を保証してくれるのでした。

この証明の面白いところは、証明の流れに沿ってプログラムを書けば、具体的に $p = X^2 + Y^2$ を満たす $X, Y$ の組を計算できるという点です。実際、 $p = 2017$ は

$2017 = 44^2 + 9^2$

とかけることもわかりました。 $p = 2017$ の場合は、実直に代入して計算してもそれほど大変ではありませんが、大きな素数に対しては難しいでしょう。一方で、今回の方法は、 $X^2 + 1 \equiv 0 \pmod{p}$ なる $X$ さえ求まれば、大きな素数に対しても高速に $X, Y$ の組を求めることが可能な方法となっています。

今回紹介した証明は、私自身も最初は難しいと感じたものでした。ところが、実際にプログラムで組んでみることによって、議論の流れをだんだんと追いかけられるようになったのです。具体的に手を動かしたことによって、とっつきやすくなったのだと思います。「プログラミングを通して数学を理解する」ということの、一つの実践例として参考にしていただけたら幸いです。

以上で、今日のお話は終わりです。

タイトルは「2017を二つの平方数の和で表す方法 (1)」としていましたが、別のアドベントカレンダー（日曜数学アドベントカレンダーの25日目）にて、「2017を二つの平方数の和で表す方法 (2)」を紹介したいと思っています。今回とは全く異なる方法で $p = X^2 + Y^2$ を計算します。

よろしければ、そちらもお楽しみください。

それでは、今日はこの辺で。