2017を二つの平方数の和で表す方法 (2) - tsujimotterのノートブック

日曜数学 Advent Calendar 2017 の 25 日目（最終日！）の記事です。

数学大好き皆様こんにちは。今日は、日曜数学アドベンター2017 最終日です！

2017 年最後ということで 2017 に関するお話です。

$p$ を $2017$ のような奇数の素数を考えたとき

「 $p = X^2 + Y^2$ なる整数 $X, Y$ を具体的に計算する方法」

を紹介したいと思います。

実はこのブログでも、「数学とコンピュータアドベントカレンダー」の記事として、ひとつの計算方法を紹介しています。
tsujimotter.hatenablog.com

今回は上記の記事とは異なる別の方法を紹介したいと思います。

「初等整数論」をある程度知っている方向けの記事になってしまいますが、面白い内容だと思いますのでよかったらご覧になってください。

ヤコブスタール和

今日の主役は「ヤコブスタール和」です。ヤコブスタール和は、以下の式で定義されます。

$\displaystyle S(a) = \sum_{x=0}^{p-1} \left( \frac{x(x^2+a)}{p} \right) \tag{1}$

この $\left( \frac{\cdot{}}{p} \right)$ は $\bmod{p}$ のルジャンドル記号です。 $x$ を $0$ から $p - 1$ まで動かしてルジャンドル記号を足し合わせて定義されます。なお、 $\left( \frac{d}{p} \right)$ は、 $d$ が $p$ で割り切れるときは 0 になると約束しておきます。

ちなみに「ヤコブスタール和」という名前ですが、ヤコブとスタールではなく、ヤコブスタール（Jacobsthal）という人名に因んでいます。tsujimotterはヤコブ・ヤコービが考えたものと勘違いしていました。一方、ヤコブスタール和は 1907 年に提唱されたので、割と最近のことのようです。

ヤコブスタール和を使うと、以下のように $p = X^2 + Y^2$ の $X, Y$ が得られます。

定理

$p$ を $p \equiv 1 \pmod{4}$ を満たす素数とし， $p$ を法として平方非剰余である整数 $n \in \mathbb{Z}$ を一つ取る．このとき， $S(1), S(n)$ はともに偶数であり，

$\displaystyle p = \left(\frac{S(1)}{2}\right)^2 + \left(\frac{S(n)}{2}\right)^2 \tag{2}$

が成り立つ．

ヤコブスタール和を用いて、 $X = S(1)/2, \; Y = S(n)/2$ と表せるということですね。 $S(1), S(n)$ はともに偶数なので、どちらも $2$ で割り切れます。

「 $n$ ってなんだよ！」とか「 $S(1)$ と $S(n)$ だけでいいの？」とか、いろいろ気になるところはあるかと思います。これらの疑問については、証明を追っていくことで解決されます。

何はともあれ、まずは具体例を計算してみましょう。

$p =5$ のとき：

$p = 5$ のとき、 $2$ は $5$ を法として平方非剰余です。したがって、 $n = 2$ とします。ここで $S(1), S(n)$ を計算しましょう。

$\displaystyle \begin{align} S(1) &= \sum_{x=1}^{4} \left( \frac{x(x^2+1)}{p} \right) \\ &= \left( \frac{1\cdot (1^2 + 1)}{5} \right) + \left( \frac{2\cdot (2^2 + 1)}{5} \right) + \left( \frac{3\cdot (3^2 + 1)}{5} \right) + \left( \frac{4\cdot (4^2 + 1)}{5} \right) \\ &= \left( \frac{ 2 }{5} \right) + \left( \frac{ 10 }{5} \right) + \left( \frac{ 30 }{5} \right) + \left( \frac{68 }{5} \right) \\ &= \left( \frac{ 2 }{5} \right) + \left( \frac{ 0 }{5} \right) + \left( \frac{ 0 }{5} \right) + \left( \frac{ 3 }{5} \right) \\ &= (-1) + 0 + 0 + (-1) = -2 \end{align}$

$\displaystyle \begin{align} S(n) &= \sum_{x=1}^{4} \left( \frac{x(x^2+2)}{p} \right) \\ &= \left( \frac{1\cdot (1^2 + 2)}{5} \right) + \left( \frac{2\cdot (2^2 + 2)}{5} \right) + \left( \frac{3\cdot (3^2 + 2)}{5} \right) + \left( \frac{4\cdot (4^2 + 2)}{5} \right) \\ &= \left( \frac{ 3 }{5} \right) + \left( \frac{ 12 }{5} \right) + \left( \frac{ 33 }{5} \right) + \left( \frac{ 72 }{5} \right) \\ &= \left( \frac{ 3 }{5} \right) + \left( \frac{ 2 }{5} \right) + \left( \frac{ 3 }{5} \right) + \left( \frac{ 2 }{5} \right) \\ &= (-1) + (-1) + (-1) + (-1) = -4 \end{align}$

よって、

$\begin{align} X &= S(1)/2 = -1 \\ Y &= S(n)/2 = -2 \end{align}$

となり、

$5 = (-1)^2 + (-2)^2$

が得られました。

計算してみるとわかりますが、 $1$ から $p-1$ まで足し合わせる必要があるので、特に大きい素数 $p$ に対してはあまり手計算向きの方法ではありません。

ルジャンドル記号の計算は工夫できるものの、基本的には機械的な計算で $X, Y$ が得られるというのが面白ポイントじゃないかなと思います。

しかし、なんでこんなことが成り立つのか不思議ですよね！というわけで、今日はこの公式を証明してみましょう！

今日使う３つの補題

今回の証明でキーとなるヤコブスタール和に関する３つの補題を紹介します。

証明はそれほど難しくないので、方針だけの紹介に留めます（詳しくは参考文献を読んでください）。ここでは証明の理解は必ずしも必要ありません。むしろ、補題の意味の理解が大事なので、その点を重点的に解説します。

補題1

$S(a)$ は常に偶数である．特に， $p \mid a$ ならば $S(a) = 0$ が成り立つ．

（証明の方針）
$p \nmid a$ のとき， $x(x^2 + a) \equiv 0 \pmod{p}$ の整数解は奇数個であるから，これ以外の $x$ はルジャンドル記号が $\pm 1$ となる． $0$ から $p-1$ までの $x$ から奇数個を除くと、偶数個なので $S(a)$ の偶数性がいえる．

$p \mid a$ のときは，ルジャンドル記号が $\left(\frac{x(x^2 + a)}{p}\right) = \left(\frac{x^3}{p}\right) = \left(\frac{x}{p}\right)$ となるから，ルジャンドル記号を全部足すと 0．

補題2

任意の整数 $a, b$ に対して， $\displaystyle S(ab^2) = \left(\frac{b}{p}\right)S(a)$ が成り立つ．

（証明の方針）
$S(a^2 b)$ の和の計算で， $x \mapsto bx$ として和をとる．

補題3

任意の整数 $c$ に対して，

$\displaystyle \sum_{x=0}^{p-1} \left( \frac{x(x+c)}{p} \right) = -1 + \begin{cases} p & (c\equiv 0 \pmod{p}) \\ 0 & (c\not\equiv 0 \pmod{p}) \end{cases} \tag{3}$

（証明の方針）
$xy \equiv 1 \pmod{p}$ となる $x$ の逆元 $y$ をとる．
$\left( \frac{x(x+c)}{p} \right)$ に $\left( \frac{y^2}{p} \right)$ をかけて， $\left(\frac{y^2}{p} \right)\left( \frac{x(x+c)}{p} \right) = \left( \frac{xy(xy+cy)}{p} \right) = \left( \frac{1+cy}{p} \right)$ と変形する．

このとき， $\sum_{y=1}^{p-1} \left( \frac{1+cy}{p} \right)$ は

(i) $p \mid c$ ならば， $\left( \frac{1}{p} \right)$ を $p-1$ 回足し合わせるから $p-1$ となる．

(ii) $p \nmid c$ ならば， $cy$ はすべての $1$ から $p-1$ を渡り， $\left( \frac{1+cy}{p} \right)$ はこれを $+1$ シフトさせたものである．つまり， $2$ から $p$ まで足し合わせることになる．しかし， $p$ のときはルジャンドル記号が 0 になるので，結局 $2$ から $p-1$ まで足し合わせるのと同じ．したがって， $\left( \frac{1}{p} \right)$ を除いてルジャンドル記号を足し合わせるわけだから（全部足すと 0）， $-1$ が得られる．

ここからは、それぞれの補題の意味を図を用いて解説します。

まず前提として、ヤコブスタール和 $S(a)$ は $\mod{p}$ で同じ値を取ることに注意します。つまり、 $S(a) = S(a + p)$ となります。これは定義から明らかですね。

f:id:tsujimotter:20171224230845p:plain:w400

さて補題 1 は、この一番左の $S(0)$ が $0$ になることを言っています。よって、実質 $S(1)$ から $S(p-1)$ の $p-1$ 個を考えれば良いわけです。

f:id:tsujimotter:20171224230859p:plain:w320

次は補題 2 ですが、これが決定的に重要な性質です。補題 2 の式を両辺 2 乗すると

$S(ab^2)^2 = S(a)^2 \tag{4}$

となります。これは、ヤコブスタール和 $S(a)$ の変数の $a$ に「なにか平方数 $b^2$ 」をかけても、ヤコブスタール和の値に変化はないということを意味します。

この事実を念頭において、 $1$ から $p-1$ までのヤコブスタール和を「変数が平方剰余であるもの」と「変数が平方非剰余であるもの」の２組に分けることにします。

なぜ、平方剰余と平方非剰余に分けるかというと、平方剰余の数に平方数をかけることで任意の平方剰余に移り変わることができ、平方非剰余の数に平方数をかけることで任意の平方非剰余に移り変わることができるからです。逆に，平方剰余と平方非剰余の間では、平方数をかけても移り変わることができません。

f:id:tsujimotter:20171224230913p:plain:w320

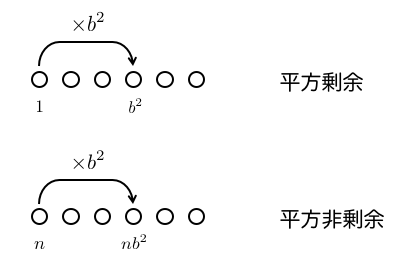
このことは、ヤコブスタール和において重要な意味を持ちます。つまり、平方剰余の $a$ に対して $S(a)$ はすべて同じ値をとり、平方非剰余の $a$ に対して $S(a)$ はすべて同じ値をとるのです。

$S(1) = S(b^2) = \cdots$

$S(n) = S(nb^2) = \cdots$

結局、ヤコブスタール和は２つの値しかとらないということですね。そのため「平方剰余の代表」である $S(1)$ と「平方非剰余の代表」の $S(n)$ だけを考えれば十分だとわかります。

そして、平方剰余・平方非剰余の個数はそれぞれ $(p-1)/2$ です。よって、全部足し合わせると

$\displaystyle \begin{align} \sum_{a=1}^{p-1} S(a)^2 &= \sum_{a : 平方剰余} S(a)^2 + \sum_{a : 平方非剰余} S(a)^2 \\ &= \frac{p-1}{2}\left\{S(1)^2 + S(n)^2\right\} \end{align}$

となり、非常に重要な式

$\displaystyle \sum_{a=1}^{p-1} S(a)^2 = \frac{p-1}{2}\left\{S(1)^2 + S(n)^2\right\} \tag{5}$

が得られます。かなり定理の式 $(1)$ に近づいてきましたね。

定理の式 $(1)$ では $S(1), S(n)$ の正体が謎でしたが、以上の議論より $S(1)$ が「平方剰余の代表」で $S(n)$ が「平方非剰余の代表」ということがわかりました。

あとは、式 $(5)$ 左辺の $\sum_{a=1}^{p-1} S(a)^2$ を別の方法で求めれば、定理の式 $(1)$ が得られます。使うのはもちろん補題 3です。

それでは、証明に移りましょう！

証明

$\sum_{a=1}^{p-1} S(a)^2$ を二通りの方法で計算します。一つ目の計算は、式 $(5)$ で得られています。

ここでは、定義通りに展開して計算します。

$\displaystyle \begin{align} \sum_{a=1}^{p-1} S(a)^2 &= \sum_{a=1}^{p-1} \sum_{x=1}^{p-1} \sum_{y=1}^{p-1} \left( \frac{x(x^2+a)}{p} \right) \left( \frac{y(y^2+a)}{p} \right) \\ &= \sum_{a=1}^{p-1} \sum_{x=1}^{p-1} \sum_{y=1}^{p-1} \left( \frac{xy(x^2+a)(y^2+a)}{p} \right) \\ &= \sum_{x=1}^{p-1} \left( \frac{x}{p} \right) \sum_{y=1}^{p-1} \left( \frac{y}{p} \right) \sum_{a=1}^{p-1} \left( \frac{(x^2+a)(y^2+a)}{p} \right) \end{align}$

ここで、

$\begin{align} (x^2+a)(y^2+a) &= (x^2 + a)(x^2 + a + y^2 -x^2) \\ &= X(X + c) \end{align}$

とします。 $X = x^2 + a, \;\; c = y^2 - x^2$ とおきました。 $X = x^2 + a$ は、 $a$ を動かしたときすべての $1$ から $p-1$ を渡ります。また、 $c\equiv 0 \pmod{p}$ という条件は $x^2 = y^2$ という条件になります。

したがって、補題 3 が使えて

$\displaystyle \sum_{a=1}^{p-1} \left( \frac{(x^2+a)(y^2+a)}{p} \right) = \sum_{X=1}^{p-1} \left( \frac{X(X+c)}{p} \right) = -1 + \begin{cases} p & (x^2 = y^2) \\ 0 & (x^2 \neq y^2) \end{cases}$

が得られます。

$-1 + p$ or $-1 + 0$ を前と後ろに分けると、まず $-1$ の方を和に入れると

$\displaystyle -\sum_{x=1}^{p-1} \left( \frac{x}{p} \right) \sum_{y=1}^{p-1} \left( \frac{y}{p} \right) = 0 \tag{6}$

となります。 $p$ or $0$ の方を考えると、 $x^2 = y^2$ のときだけ考えれば良いから、このときは

$\displaystyle p\sum_{x, y: x^2 = y^2} \left( \frac{x}{p} \right) \left( \frac{y}{p} \right)$

を考えれば良いです。 $x^2 = y^2$ ということは、 $y = x$ か $y = -x$ というわけです。前者の場合は

$\displaystyle \left( \frac{x}{p} \right) \left( \frac{y}{p} \right) = \left( \frac{x}{p} \right) \left( \frac{x}{p} \right) = +1$

となり、後者の場合は

$\displaystyle \left( \frac{x}{p} \right) \left( \frac{y}{p} \right) = \left( \frac{x}{p} \right) \left( \frac{-x}{p} \right) = \left( \frac{-1}{p} \right) = +1$

です。最後の等式は、 $p \equiv 1 \pmod{4}$ であることから従います。

したがって、 $p-1$ 個の $x$ に対して、 $y = \pm x$ の 2 個を考えて、すべての $+1$ を足し合わせることから、

$\displaystyle p\sum_{x, y: x^2 = y^2} \left( \frac{x}{p} \right) \left( \frac{y}{p} \right) = 2p(p-1) \tag{7}$

となります。

式 $(6), (7)$ を合わせて

$\displaystyle \sum_{a=1}^{p-1} S(a)^2 = 2p(p-1) \tag{8}$

が得られます。

これが２通り目の和の計算結果です。これらの結果が一致することから、

$\displaystyle 2p(p-1) = \frac{p-1}{2}\left\{S(1)^2 + S(n)^2\right\} \tag{9}$

となって、両辺 $2(p-1)$ で割ると

$\displaystyle p = \frac{1}{4}\left\{S(1)^2 + S(n)^2\right\} \tag{10}$

が得られます。これが求めたかった式でした。証明終わり！

$2017 = X^2 + Y^2$ の計算

さて、せっかく定理が証明できましたので、ヤコブスタール和を使って $p = 2017$ を計算してみましょう。

まず、 $\bmod{p}$ の平方非剰余ですが、たとえば $3$ とかはどうでしょうか。平方剰余の相互法則より

$\displaystyle \left(\frac{3}{2017}\right) = \left(\frac{2017}{3}\right) = \left(\frac{1}{3}\right) = 1$

となり、平方剰余でした。平方剰余であればもう一度別の数で試します。

$\displaystyle \left(\frac{5}{2017}\right) = \left(\frac{2017}{5}\right) = \left(\frac{2}{3}\right) = -1$

よって、 $5$ は $2017$ の平方非剰余ですね。したがって、 $n = 5$ とします。

あとは、 $S(1), S(n)$ をそれぞれ計算するだけです。しかしながら、これを実施するためには、 $p-1 = 2016$ 個のルジャンドル記号を計算する必要があります。ちょっと手計算では無理そうなので、コンピュータで計算してもらいましょう。

Ruby のプログラムを置いておきます。

jacobsthal.rb · GitHub

jacobsthal.rb という名前をつけてターミナルで

$ ruby jacobsthal.rb

と実行すると計算されます。

結果として、

$S(1) = -18$

$S(n) = -88$

が得られました。ともに偶数になっていますので、2 で割ると $X = -9, \; \; Y = -44$ が求まります。

実際、

$2017 = (-9)^2 + (-44)^2$

が成り立ちますね！！

これにて、 $p = 2017$ を二つの平方数の和で表すことができました！お疲れ様です！

参考文献のおすすめ

最後に、参考文献の紹介です。

今回私が参照したのは「素数と２次体の整数論」という本です。

素数と2次体の整数論 (数学のかんどころ 15)

作者: 青木昇,飯高茂,中村滋,岡部恒治,桑田孝泰
出版社/メーカー: 共立出版
発売日: 2012/12/21
メディア: 単行本
購入: 2人クリック: 2回
この商品を含むブログを見る

この本の５章の応用例としてヤコブスタール和が紹介されています。本記事の証明方法も、基本的にこの本の記述を参考にしています。

私はこの「素数と２次体の整数論」はすごくいい本だと思っています。誤植が多かったり、厳密に議論していないところがあったりして、ネット上では割と評判がよくないのですが、それでも私はこの本をおすすめしたいと思っています。

その証拠に、私のブログ記事の中に、この本をネタ元にした記事がたくさんあります。ほんとにたくさんあるので「素数と２次体の整数論」のタグで探してみてください。
tsujimotter.hatenablog.com

私がなぜこの本をここまでプッシュするかというと、それはこの本が「数論を伝えたいという著者の愛に溢れている」と思うからです。

今回の「ヤコブスタール和」の話は、なかなか聞いたことがない話かと思います。実際、「ヤコブスタール和」で検索してみても、この話が載った和書が出てきません。

しかしながら、誰しも一度は考えるとおもうのです。 $p = 4n + 1$ のとき $p = X^2 + Y^2$ と書けることはわかったけど、実際 $X, Y$ は求められるのだろうかと。

普通の数論の本であれば $p = X^2 + Y^2$ の式を具体的に求めたりはしなくて、そのまま平方剰余の相互法則に向かってしまいますが、素数と２次体の整数論はこうした疑問に答えようとしてくれています。これは、著者の方の「数論を楽しんでもらいたい」という気持ちの表れだと思うのです。この本は、こうした読者の興味をかきたてるような具体例や応用例に富んでいて、いたるところの説明に創意工夫がなされています。

今回の記事を読んで、興味を持ってくださった方は、ぜひこの本を手に取ってみてください。