続：7は合同数（計算機編） - tsujimotterのノートブック

ここ最近「合同数」について勉強し、理解度が上がってきました。そこで、今日は合同数の具体的な計算をやってみたいと思います。

今回は「7は合同数」の記事に出てきた「あの三角形」を計算で求めてみましょう。
tsujimotter.hatenablog.com

SageMathについて

今回の記事は、次のツイートの解説という位置付けです。

Sagemathを使って合同数に付随する楕円曲線の（無限位数の）有理点を計算することで、面積が 7 になる直角三角形の辺の長さ (35/12, 24/5, 337/60) を具体的に計算できた！楽しい！

参考：7は合同数 https://t.co/dkNotmbQ8B pic.twitter.com/f9WuUrRsYc
— tsujimotter (@tsujimotter) 2018年9月30日

計算には、SageMathというソフトウェアを用いて行います。
www.sagemath.org

CoCalcというサービスを使えば、オンラインでもSageMathが扱えます。TwitterやGithub等のアカウントでログインすることができますので、自分でも試したい方はアクセスしてみてください。

https://cocalc.com/app

復習：合同数の性質

合同数の性質について簡単に復習しましょう。

まず、合同数の定義は「すべての辺の長さが有理数であるような直角三角形の面積になる整数」のことです。図で表すとこんな感じです。

f:id:tsujimotter:20180924210627p:plain:w200

たとえば、6は合同数です。いつもの3:4:5の直角三角形を考えれば、その面積が6になることがすぐに確認できます。

f:id:tsujimotter:20180924210804p:plain:w200

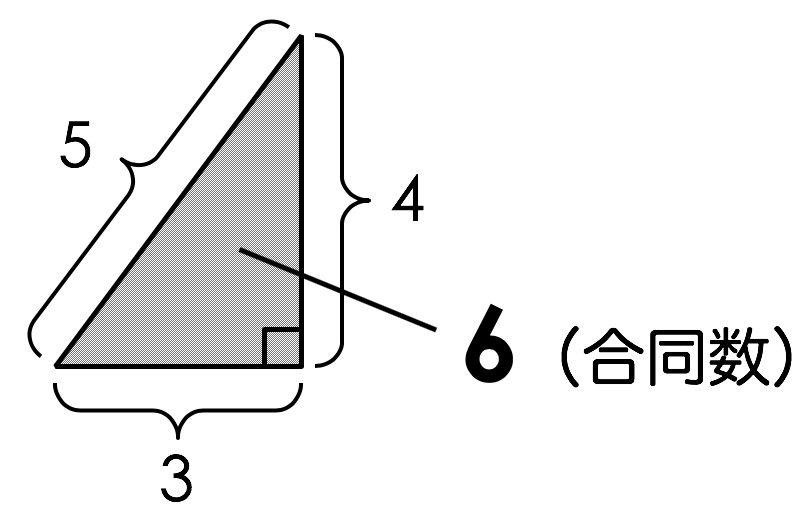
また、合同数の定義は、次のように数式で表すことができます。

$n$ が合同数であるとは

$\begin{cases} X^2 + Y^2 = Z^2 \\ \cfrac{XY}{2} = n \end{cases} \tag{1}$

を満たす $X, Y, Z \in \mathbb{Q}$ が存在するということである。

$X^2 + Y^2 = Z^2$ はピタゴラスの定理によって直角三角形になるという条件で、もう一つは $n$ がその直角三角形の面積になるという条件ですね。

以上の式は、適当な変数変換を施すことで楕円曲線の方程式に帰着できます。 $n$ が合同数であるときの $(X, Y, Z) \in \mathbb{Q}^3$ の組が存在するとき

$\begin{align} x &= (Z/2)^2, \\ y &= Z(X+Y)(X−Y)/8 \end{align} \tag{2}$

という変数変換を施すことで、次の楕円曲線 $E_n$ の方程式に帰着できるのです。

$E_n : y^2 = x^3 - n^2 x \tag{3}$

逆に、楕円曲線 $E_n$ の有理点があったとして、合同数の条件を満たす直角三角形を作ることができるでしょうか。

実は、 $(x, y) \in E_n(\mathbb{Q})$ が $E_n(\mathbb{Q})$ の２倍点であり、かつ $y > 0$ であるとき、逆方向の変数変換 $(x, y) \mapsto (X, Y, Z)$ によって、合同数の条件を満たす $(X, Y, Z)$ の組が得られることがわかっています。

このような $(x, y) \in E_n(\mathbb{Q})$ が与えられたとき

$\begin{align} X &= \sqrt{x + n} - \sqrt{x - n}, \\ Y &= \sqrt{x + n} + \sqrt{x - n} \\ Z &= 2\sqrt{x} \end{align} \tag{4}$

という変数変換によって、合同数の条件を満たす $(X, Y, Z)$ の組が得られます。

ルートをとっている部分が大丈夫か気になるかもしれませんが、上の条件を満たす場合には $x, x+n, x-n$ が平方数であることが示せるので問題はありません。

なお「 $P \in E_n(\mathbb{Q})$ として $2P = (x, y)$ かつ $y > 0$ 」という条件は、 $P$ が位数有限の場合成り立たないことが確認できます。したがって、 $P$ として無限位数の点を選ぶ必要があります。

このことから、合同数の条件は $E_n$ を用いて次のように表せるのでした。

$n \; \text{は合同数} \;\; \Longleftrightarrow \;\; \operatorname{rank} E_n (\mathbb{Q}) > 0 \tag{5}$

ランクの計算は、楕円曲線のL関数を使って計算できることは「合同数問題と保型形式」の記事で示しました。
tsujimotter.hatenablog.com

今回はSageMathを使って直接生成元を計算することを考えましょう。SageMathでは、生成元を計算する裏で、2-descent法を使った計算が行われているようです。
tsujimotter.hatenablog.com

「7は合同数」の三角形の計算

それでは、SageMathを使って、実際に $n = 7$ の場合に計算してみましょう。

まずは、SageMathのワークシートを開いて、以下のコマンドを打ち込みます。

# n: 判定したい合同数
n = 7

# n に対応する楕円曲線 E_n : y^2 = x^3 - n^2 x
E = EllipticCurve([0,0,0,-n^2,0]); E

# E をプロット
plot(E)

打ち込んだらShift+Enterを押してみましょう。すると以下の結果が返ってくるはずです。

f:id:tsujimotter:20180930144741p:plain:w400

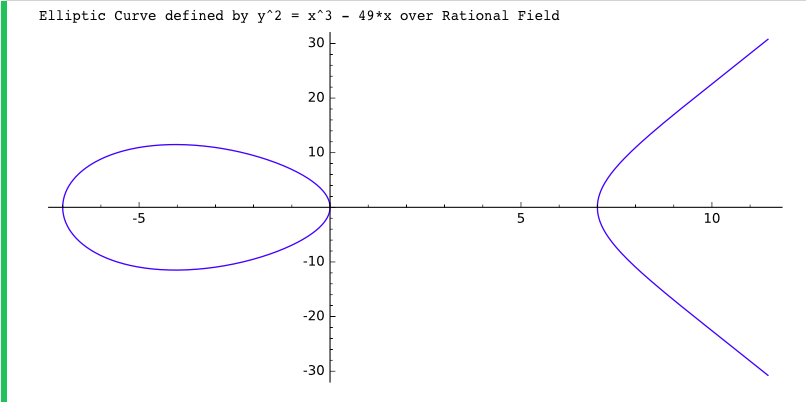
せっかくなので、楕円曲線のグラフも表示してみました。

さて、次に以下のコマンドを打ち込みましょう。

# E_n の無限位数の点の生成元（生成元が存在すれば、n は合同数）
E.gens()

ここでは楕円曲線の無限位数の点の生成元を計算しています。問題なければ次の結果が返ってきます。

[(25 : 120 : 1)]

これは、 $E_n(\mathbb{Q})$ の無限位数の点が $P = (25, 120)$ によって生成されることを示しています。

この計算の裏では、2-descent法を使って生成元の高さの上限を求めて、その上限以下の元を探索するという高度な計算が行われています。*1

なお、 $(25 : 120 : 1)$ という表示は、射影曲線としての斉次座標 $(X : Y : Z)$ を表しています。アフィン座標 $(x, y)$ に直すには、 $(x, y) = (X/Z, Y/Z)$ とすればよいです。この場合は $Z = 1$ なので、最初の二つの座標をそのまま取り出せばOKです。

続いて、 $P = (25, 120)$ の２倍点 $Q = 2P$ を計算しましょう。

# 生成元を P とする
P = E.gens()[0]; P

# P の2倍点 (x : y : 1) を求める（y > 0 であれば合同数の三角形に対応する）
Q = 2*P; Q

結果は以下のとおり：

(25 : 120 : 1)
(113569/14400 : 17631503/1728000 : 1)

よって

$\displaystyle Q = 2P = \left(\frac{113569}{14400}, \frac{17631503}{1728000}\right)$

であることがわかりました。y座標が正なので、問題ありませんね。

もしy座標が負の場合は、 $Q = -2P$ とすれば問題ありません。

さぁ、いよいよ直角三角形の辺の長さを求めましょう。式 $(4)$ の変換によって、 $Q = (x, y)$ から $X, Y, Z$ を計算してあげましょう。（以下のプログラムでは、 $X, Y, Z$ の代わりに $a, b, c$ を用います）

# 点 Q の x, y 座標を取り出す
x = Q[0]
y = Q[1]

# 直角三角形の辺の長さ (a, b, c)
a = sqrt(x+n) - sqrt(x-n); a
b = sqrt(x+n) + sqrt(x-n); b
c = 2*sqrt(x); c

結果は以下のとおりです。

35/12
24/5
337/60

$\begin{align} X &= 35/12 \\ Y &= 24/5 \\ Z &= 337/60 \end{align} \tag{6}$

これが求める直角三角形の辺になっていることは式 $(1)$ を使って次のように確認できます。

# ピタゴラスの定理が成り立っているか確認
a^2 + b^2 == c^2

# 面積が n になっていることを確認
a*b/2 == n

True
True

たしかに成立していますね！

というわけで「7は合同数」の直角三角形を楕円曲線を使って計算することができました！

f:id:tsujimotter:20160228002053p:plain:w320

めでたしめでたし！

おまけ：157は合同数

せっかくなので、 $n = 157$ の場合でも同じように計算してみました。

結果はこちら：

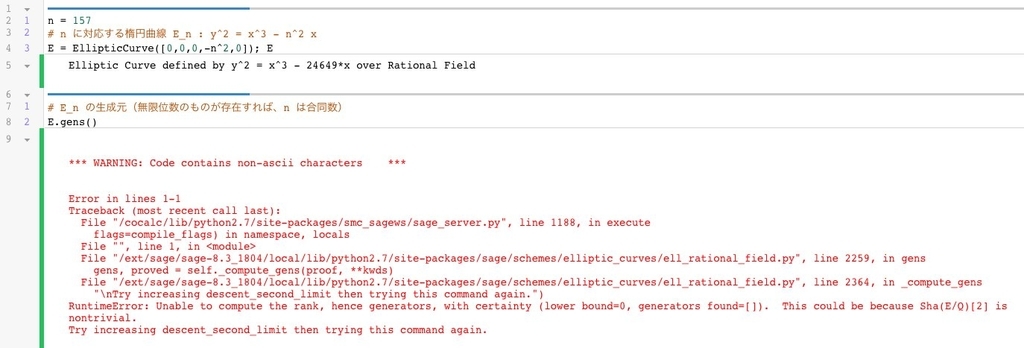
残念ながら、E.gens() の計算でエラーを掃いてしまいました。

原因はよくわかっていませんが

This could be because Sha(E/Q)[2] is nontrivial.

とエラーが出ているので、もしかするとテイト・シャファレビッチ群の非自明性に問題があるかもしれません。

2-descentを実行するときには、セルマー群を通して $E(\mathbb{Q})/2E(\mathbb{Q})$ の大きさを評価するのですが、完全系列からテイト・シャファレビッチ群の分のずれがあります。したがって、テイト・シャファレビッチ群が非自明な場合は、うまく評価できないということなのでしょうか。
tsujimotter.hatenablog.com

上の記事に書いたことが、こんなところに現れるなんて面白いですね！計算してみるもんですね。

参考記事

tsujimotter.hatenablog.com

SageMathのリファレンス

より進んだ数学 — Sage チュートリアル v9.1

横山俊一「計算する立場からの楕円曲線論入門」，山形大学理学部数理科学科2014 年度後期「数理情報特選F/数理科学特別講義E」講義資料1
http://www2.math.kyushu-u.ac.jp/~s-yokoyama/lectures/2015-2018/files/2014Yamagata.pdf

*1:たぶん。もしかしたら嘘を言っているかもしれません。。。