楕円曲線の有理点のランクを計算しよう！（2-descentの具体的計算）

楕円曲線

$E\colon y^2 = x^3 - x$

には、有理点が

$\newcommand{\qq}{\mathbb{Q}}E(\qq) = \{ \mathcal{O}, (0, 0), (1, 0), (-1, 0) \}$

の4点しか存在しないことが知られています。特に、無限位数の点は存在しません。

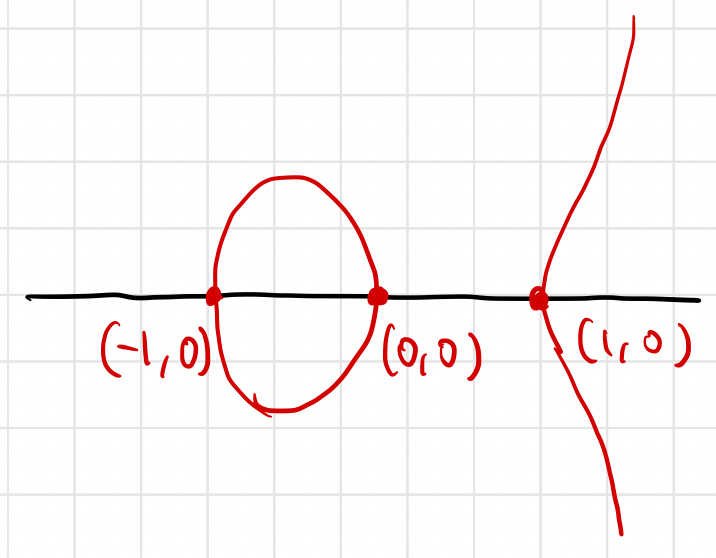
今日考えたいのは「無限位数の点が存在しないことを本当に証明できるのか？」という問題です。実際、それは可能であるというのが、今日伝えたいことです。

2-descent という方法を用いると、無限位数の有理点のランクを決定できます。ランクとは無限位数の点を生成する点（生成点）の個数であり、これが 0 であることが示せれば無限位数の点がないこと意味します。

記事の最後でも触れたいと思いますが、上記の楕円曲線のランクを決定することで、「 $1$ は合同数でないこと」や「 $n = 4$ のフェルマーの最終定理」を証明することができてしまいます。こんな風に、応用の上でもとても楽しいトピックになっています。よろしければ最後までお付き合いください。

目次：

今日の参考文献

2-descentとは (1)：モーデルの定理

2-descentとは (2)：E(ℚ)/2E(ℚ)とE(ℚ)のランクの関係

2-descentとは (3)：キーアイデア

2-descentとは (4) ：謎の準同型写像 δ, δ'

2-descentとは (5)：im(δ') の決定

(a) y = 0 のとき：

(i) x = 0 のとき：

(ii) x ≠ 0 のとき：

(b) y ≠ 0 のとき（つまり、x ≠ 0 ）：

2-descentとは (6)：結論

例１： E: y² = x³ - x, E': Y² = X³ + 4X の場合

#im(δ') の計算：

#im(δ) の計算：

ランク r の決定と E(ℚ) の決定：

応用：1は合同数ではない

応用：フェルマーの最終定理（n = 4 のとき）

例２： E: y² = x³ - 5x, E': Y² = X³ + 20X の場合

#im(δ') の計算：

#im(δ) の計算：

ランク r の決定：

続き：3は合同数ではない

かなり長い記事になってしまいますので、急いでいる方は具体的な手法を紹介している「2-descentとは (6)：結論」まで飛んでくれてかまいません。

もちろん、そこだけ読んでも背景となる知識は書いていませんので、可能であれば通して読んでいただけると嬉しいです。

今日の参考文献

今日の内容は、シルヴァーマン・テイトの「楕円曲線論入門」という本を参考にしています。基本的には、こちらの本の流れを参考に記事をまとめています。

楕円曲線論入門

作者:J. H. シルヴァーマン,J. テイト
丸善出版

Amazon

該当箇所は第３章「有理点のなす群」です。

最近「ロマ数トレラン楕円曲線入門オンラインセミナー」というゼミに参加しているのですが、使っている教科書が上記の本です。その関係で、最近じっくり読み込んでいます。

今、次の節で示す「モーデルの定理」の証明を勉強していて、楕円曲線論入門を予習していたらとても面白い内容だったので、記事にまとめてみたくなったというのが経緯です。ロマ数トレランには、楕円曲線を勉強するモチベーションをいただいて大変感謝しております。

また、下記のPDFでは、ガロアコホモロジーやセルマー群といった、より高い視点から書かれていて、その意味で大変勉強になりました。

後藤丈志「古典的 Diophantus 問題に対応する楕円曲線のセルマー群と有向グラフ」
https://www.ma.noda.tus.ac.jp/u/ha/SS2006/Data/Hokoku/goto.pdf

横山先生のこちらの講義資料も大変役に立つかと思います：

横山俊一「計算する立場からの楕円曲線論入門」
http://www.comp.tmu.ac.jp/s-yokoyama/lectures/2015-2018/files/2014Yamagata.pdf

なお、楕円曲線の基礎的な事項について関心がある方は、手前味噌ですが
tsujimotter.hatenablog.com

や
note.com

を読んでいただくとよいかと思います。

2-descentとは (1)：モーデルの定理

$E$ を $\qq$ 上の楕円曲線（定義方程式の係数がすべて有理数であるということ）とします。上の例で挙げた $E\colon y^2 = x^3 - x$ も係数は有理数ですね。

楕円曲線の点には一般に「加法」の演算が入り、その演算によって $E$ は群構造を持ちます。また、 $E$ の有理点（座標が有理数の点）全体だけを考えても、部分群をなします。これを $E(\qq)$ と書くことにします。

このとき、一般に次の事実が成り立つという「大定理」が知られています：

定理（モーデル）

$E(\qq)$ は有限生成アーベル群

このモーデルによる定理は、楕円曲線の理論において大変重要な定理の一つです。なぜ重要かというと、 $E(\mathbb{Q})$ の群構造を理解することにつながるからです。

実際、有限生成アーベル群の構造定理により、 $E(\qq)$ は次のような同型を持ちます：

$\newcommand{\zz}{\mathbb{Z}}E(\qq) \simeq \zz^r \oplus \zz/p_{1}^{v_1}\zz \oplus \cdots \oplus \zz/p_{s}^{v_s}\zz$

ここで、 $r$ は $E(\qq)$ のランクといって、 $E(\qq)$ の自由部分の生成点の個数を表します。 $\newcommand{\rank}{\operatorname{rank}}r = \rank E(\qq)$ とも表します。後半の $\zz/p_{1}^{v_1}\zz \oplus \cdots \oplus \zz/p_{s}^{v_s}\zz$ は有限位数の部分群に対応するパートです。

$E(\qq)$ の群構造を考えるときに、有限位数の部分群の構造はNagell-LutzやMazurによってアルゴリズム的に特定することができます。

一方で、ランク $r$ を特定することができれば、 $E(\qq)$ の群構造を完全に理解したことになるわけですが、そこで使えるのが2-descentというわけです。

今回は、簡単のため $\qq$ 上の楕円曲線として

$E \colon y^2 = x^3 + ax^2 + bx$

という形の曲線に限定しておきたいと思います。つまり右辺の定数項はないものを考えます。

このように限定しておくと

$E \colon y^2 = x(x^2 + ax + b)$

と分解でき、 $x^2 + ax + b$ が2次式になるのがポイントです。

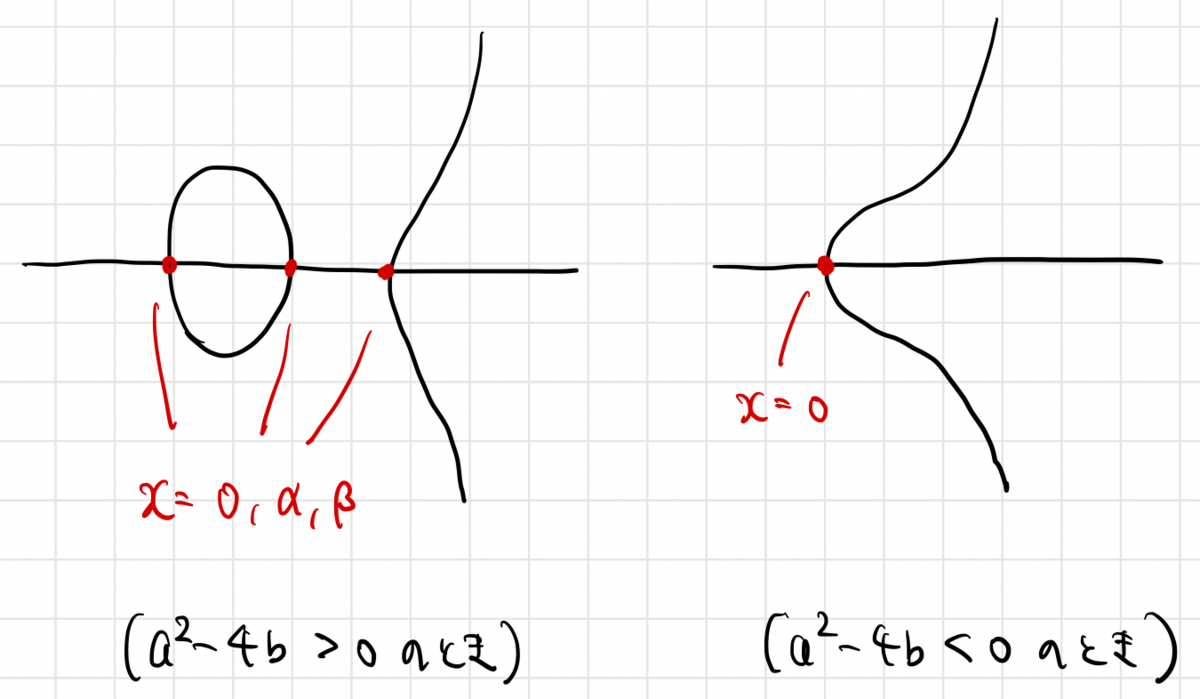
楕円曲線の定義から、右辺の多項式は重根を持たないので、 $x^2 + ax + b$ は2つの相異なる実数解 $x = \alpha, \beta$ を持つか、実数解を持たないかのいずれかになります。右辺が $0$ のとき $y = 0$ となるので、これはつまり $E$ が $x$ 軸とどのように交わるかを表していると言えます。

ここで、2倍写像

$\begin{align} [2] \colon E &\longrightarrow E, \\ P &\longmapsto 2P \end{align}$

を考えます。これは同種写像と呼ばれる写像になっています。

注：同種写像とは、楕円曲線 $(E, \mathcal{O})$ から $(E', \mathcal{O}')$ への 0 ではない有理写像であって、 $E$ の無限遠点 $\mathcal{O}$ を含むすべての点で定義される写像（正則写像）であり、 $\mathcal{O}$ を $\mathcal{O}'$ に写すものとして定義されます。

また、一般論として同種写像は準同型写像（楕円曲線の群構造を保存する写像）となっています。

注：もちろん、この一般論を使わずとも $[2]$ が準同型写像であることはわかります。

さらに、これまた一般論により楕円曲線の同種写像は全射なので、以下の完全列が成り立ちます：

$0 \longrightarrow E[2] \longrightarrow E \xrightarrow{\;[2] \;} E \longrightarrow 0$

ここで、 $\newcommand{\ker}{\operatorname{ker}}E[2] = \ker[2]$ です。

一方で、 $[2]$ を $E$ の部分群 $E(\qq)$ に制限させたものをあらためて $[2] \colon E(\qq) \to E(\qq)$ とすると、この像は一般に $E(\qq)$ には一致しません。すなわち、全射ではないということです。

注：ここは、私が以前混乱した部分です。 $[2]\colon E\to E$ が全射だからといって、 $[2]\colon E(\qq) \to E(\qq)$ が全射であるとは限らないというのです（むしろ、一般には全射になりません。）。

たとえば、同様の例として以下の写像を考えれば、納得できるかもしれません。

$\begin{align} \varphi\colon \mathbb{C}^\times &\longrightarrow \mathbb{C}^\times, \\ x & \longmapsto x^2 \end{align}$

これは明らかに全射です。

一方で、これを $\qq^\times$ に制限したものを考えると

$\begin{align} \varphi\colon \qq^\times &\longrightarrow \qq^\times, \\ x & \longmapsto x^2 \end{align}$

となりますが、これは全射ではありませんね。

たとえば、 $\varphi(\sqrt{2}) = 2$ を考えれば良いでしょう。 $2 \in \qq^\times$ ですが $\sqrt{2} \not\in \qq$ ですね。

したがって、 $[2] \colon E(\qq) \longrightarrow E(\qq)$ の像を $2E(\qq)$ と表すと、

$E(\qq)/2E(\qq)$

という群が意味を持つことになります。

2-descentは、この $E(\qq)/2E(\qq)$ を通して $\rank E(\qq)$ を調べる方法です。

2-descentとは (2)：E(ℚ)/2E(ℚ)とE(ℚ)のランクの関係

今、モーデルの定理と有限生成アーベル群の構造定理より

$E(\qq) \simeq \zz^r \oplus \zz/p_1^{v_1} \zz \oplus \cdots \oplus \zz/p_s^{v_s} \zz$

と表すと、この2倍は

$2E(\qq) \simeq (2\zz)^r \oplus 2\zz/p_1^{v_1} \zz \oplus \cdots \oplus 2\zz/p_s^{v_s} \zz$

となります。

よって、上の群を下の群で割ると

$\displaystyle E(\qq)/2E(\qq) \simeq (\zz/2\zz)^r \oplus \frac{\zz/p_1^{v_1}\zz}{2\zz/p_1^{v_1}\zz} \oplus \cdots \oplus \frac{\zz/p_s^{v_s}\zz}{2\zz/p_s^{v_s}\zz}$

となります。 $\zz/2\zz$ は有限であり、各 $\frac{\zz/p^{v}\zz}{2\zz/p^{v}\zz}$ も有限なので、 $E(\qq)/2E(\qq)$ は有限群です。

注：このように、 $E(\qq)$ が有限生成であることから、 $E(\qq)/2E(\qq)$ が有限であることは直ちに従います。

逆に、 $E(\qq)/2E(\qq)$ が有限であることからは、 $E(\qq)$ が有限生成であることは「そのままでは」従いません。

しかしながらモーデルの定理は、 $E(\qq)/2E(\qq)$ の有限性と、高さ関数を用いたいくつかの補題によって、魔法のように $E(\qq)$ が有限生成であることを示してしまいます。

ここで、 $j = 1, \ldots, s$ に対して $\frac{\zz/p_j^{v_j}\zz}{2\zz/p_j^{v_j}\zz}$ の構造を考えます。

$p_j \neq 2$ のとき、 $2$ と $p_j^{v_j}$ は互いに素なので、 $\bmod{p_j^{v_j}}$ における $2$ の逆元は存在します。したがって、 $\zz/p_j^{v_j}\zz$ における2倍写像は全射となります。

ゆえに

$\displaystyle \frac{\zz/p_j^{v_j}\zz}{2\zz/p_j^{v_j}\zz} \simeq \begin{cases} \zz/2\zz & (p_j = 2) \\ 0 & (p_j \neq 3) \end{cases}$

となります。

よって

$(E(\qq) : 2E(\qq) ) = 2^r \cdot 2^{(p_j = 2 \; \text{となる } j \text{ の個数})}$

となるわけです。

$2^{(p_j = 2 \; \text{となる } j \text{ の個数})}$ の部分ですが、これは結局 $E(\mathbb{Q})$ において $2$ 倍して $\mathcal{O}$ になる点の個数に他なりません。したがって

$E(\qq)[2] = \{ P \in E(\qq) \mid 2P = \mathcal{O}\}$

と定義して

$(E(\qq) : 2E(\qq) ) = 2^r \cdot \#E(\qq)[2]$

が成り立ちます。

ここで、 $\#E(\qq)[2]$ について考えたいのですが、最初に制限した楕円曲線の形式 $E\colon y^2 = x^3 + ax^2 + bx$ によって、この部分の議論が随分と簡単になります。

$2P = \mathcal{O}$ となる点 $P$ は、

$P = \mathcal{O}$ （無限遠点）
位数 2 の点

のいずれかですが、位数2の点の $y$ 座標は $y = 0$ であることがわかります。したがって、 $0 = x^3 + ax^2 + bx$ の解が位数2の点のx座標の点の候補となります。

$x = 0$ のとき明らかに解となりますが、この座標に対応する有理点を $T = (0, 0)$ と名付けておきましょう。あとで何度も使います。

残りの解は、2次方程式 $x^2 + ax + b = 0$ の解です。解の公式より

$\displaystyle x = \frac{-a \pm \sqrt{a^2 - 4b}}{2}$

が有理数になるとき、 $(x, 0)$ が $E(\mathbb{Q})[2]$ の点となるわけです。これは明らかに、判別式 $a^2 - 4b$ が平方数になるときに限られます。

すなわち、次が言えます：

$\displaystyle \# E(\qq)[2] = \begin{cases} 4 & (a^2 - 4b \; \text{が平方数}) \\ 2 & (a^2 - 4b \; \text{が平方数ではない}) \end{cases}$

2-descentとは (3)：キーアイデア

あとは、 $(E(\qq) : 2E(\qq))$ を計算すればランク $r$ が決定できることになりました。実際、どのようにすればよいでしょうか。

キーとなるアイデアは、2倍写像を2つの同種写像に分解することです。2つの楕円曲線

$E \colon y^2 = x^3 + ax^2 + bx$

$E' \colon Y^2 = X^3 - 2aX^2 + (a^2 - 4b)X$

に対し、次のような2つの同種写像を考えます：

$\phi \colon E \longrightarrow E', \;\; (x, y) \longrightarrow \left(\frac{y^2}{x^2}, \; \frac{y(x^2 - b)}{x^2}\right)$

$\psi \colon E' \longrightarrow E, \;\; (X, Y) \longrightarrow \left(\frac{Y^2}{4X^2}, \; \frac{Y(X^2 - (a^2 - 4b) )}{8X^2}\right)$

これらを合成すると

$\psi \circ \phi = [2]_E, \;\; \phi \circ \psi = [2]_{E'}$

となっています。

これらの写像は、定義を見ただけでは意味不明なのですが、幾何的には次のような意味を持っています。

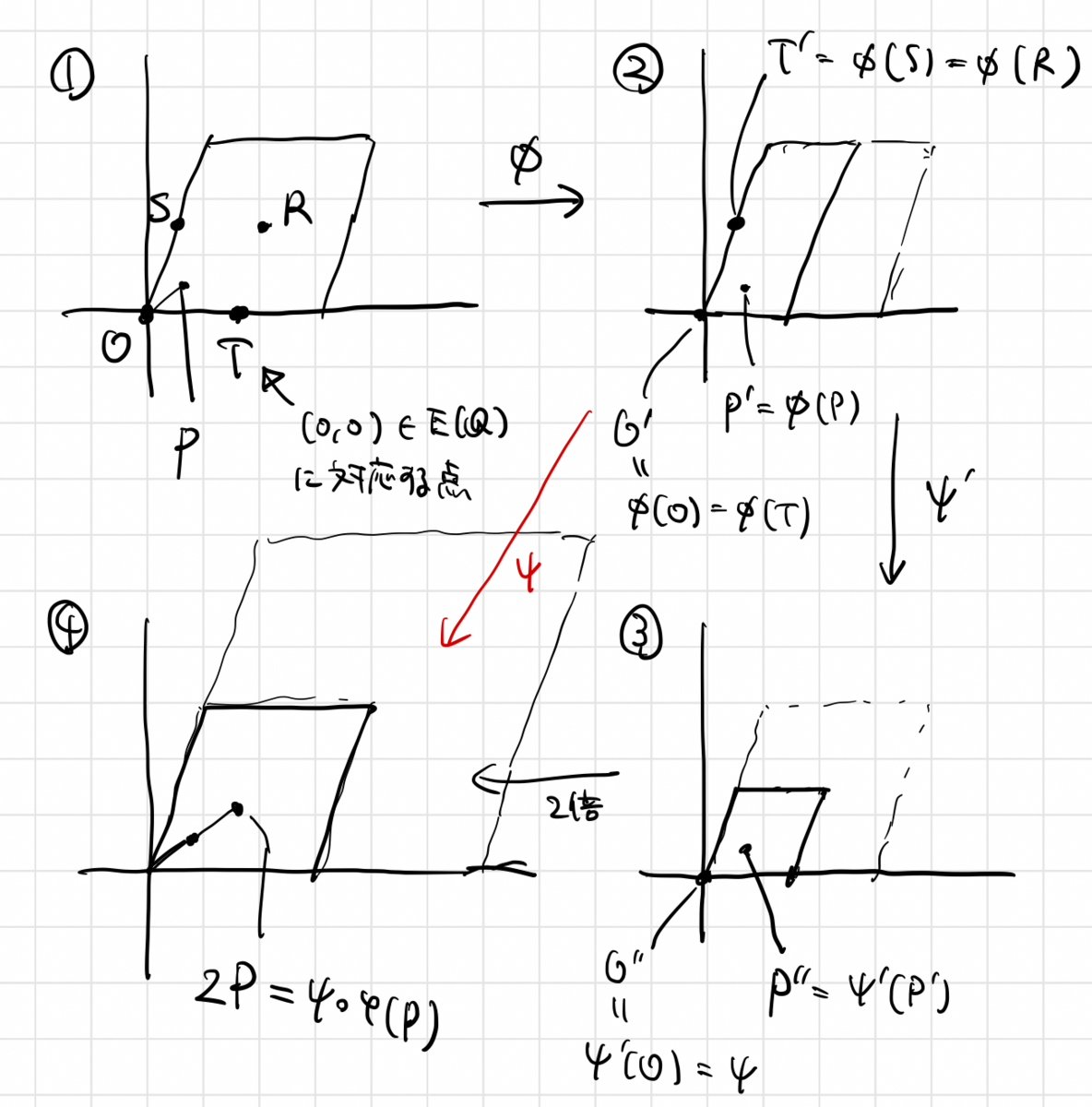
楕円曲線を複素トーラスで表すと、①のような図形になります。

位数 2 の点が $T, S, R$ の3点ありますが、これらの1つが $(0, 0) \in E(\qq)$ に対応する点で、これを $T$ と呼んでいます。

ここで $\phi(T) = \phi( \mathcal{O} )$ となるように、トーラスの左半分と右半分を同一視するような写像が $\phi$ です（②）。これはリーマン面の二重被覆になっています。

さらに、 $(0, 0) \in E'(\mathbb{Q})$ に対応する点 $T'$ を考えて、 $\psi'(T') = \psi'(\mathcal{O}')$ となるようにトーラスの上半分と下半分を同一視すると、③のように「1/4サイズ」のトーラスができます。

最後に、全体を2倍する写像を考えると、元々のトーラスに重なり、点 $P$ が合成写像で $2P$ に写るという寸法です（④）。

$\psi'$ と全体を2倍する写像を合成したものを $\psi$ としています。

よって、

$(E(\qq) : 2E(\qq)) = (E(\qq) : \psi \circ \phi( E(\qq) ) )$

となります。

$\phi, \psi$ の合成の様子を包含関係に着目して図に表すと、次のようになります；

部分群の包含列 $2E(\qq) \subset \psi( E'(\qq) ) \subset E(\qq)$ より

$\displaystyle (E(\qq) : 2E(\qq) ) = (E(\qq) : \psi(E'(\qq) ) ) \cdot \underline{(\psi(E'(\qq) ) : \psi \circ \phi(E(\qq) ) )}$

となります。

$A = E'(\qq), \;\; B = \phi( E(\qq) )$ とおくと、包含関係を考えて $B \subset A$ となりますが、下線部は $(\psi(A) : \psi(B) )$ となります。

ここで、群論の一般論により

$\displaystyle \psi(A)/\psi(B) \simeq \frac{A}{(B + \ker(\psi) )} \simeq \frac{A/B}{(B + \ker(\psi) ) / B} \simeq \frac{A/B}{\ker(\psi) / (\ker(\psi) \cap B)}$

となります。

再度 $A, B$ に代入すると

$\displaystyle \psi( E'(\qq) )/\psi\circ \phi( E(\qq) ) \simeq \frac{E'(\qq) / \phi( E(\qq) )}{\ker(\psi) / (\ker(\psi) \cap \phi( E(\qq) ))}$

となります。

ゆえに、

$\displaystyle (E(\qq) : 2E(\qq)) = \frac{(E(\qq) : \psi( E'(\qq) ) ) \cdot (E'(\qq) : \phi( E(\qq) ) )}{(\ker(\psi) : \ker(\psi) \cap \phi( E(\qq) ) )}$

となります。

ここで、分母を考えたいのですが $\phi, \psi$ の定義を考えて

$\ker(\phi) = \{ \mathcal{O}, \; T = (0, 0) \}$

$\ker(\psi) = \{ \mathcal{O}', \; T' = (0, 0) \}$

であることに注意します。

ここで、 $T' = (0, 0) \in \phi( E(\qq) )$ である必要十分条件は、 $a^2 - 4b$ が平方数であることに注意します。

$\phi\colon E \to E'$ の定義は

$\phi(x, y) = \left(\frac{y^2}{x^2}, \; \frac{y(x^2 - b)}{x^2}\right)$

でしたが、 $\phi(x, y) = (0, 0)$ であるような $(x, y) \in E(\qq)$ が存在する必要十分条件を与えよという問題です。

$y^2/x^2 = 0$ より $y = 0$ かつ $x \neq 0$ です。したがって、有理数 $x$ は $x^2 + ax + b$ の解というわけですが、この解が存在する必要十分条件は $a^2 - 4b$ が平方数であることでした。

したがって、

$(\ker(\psi) : \ker(\psi) \cap \phi( E(\qq) ) ) = \begin{cases} 1 & (a^2 - 4b\; \text{が平方数}) \\ 2 & (a^2 - 4b\; \text{が平方数ではない}) \end{cases}$

となります。

さてここで、これまでの議論により

$\displaystyle 2^r \cdot \#E(\mathbb{Q})[2] = (E(\qq) : 2E(\qq)) = \frac{(E(\qq) : \psi( E'(\qq) ) ) \cdot (E'(\qq) : \phi( E(\qq) ) )}{(\ker(\psi) : \ker(\psi) \cap \phi( E(\qq) ) )}$

が成り立つというわけですが、

$\displaystyle \# E(\qq)[2] = \begin{cases} 4 & (a^2 - 4b \; \text{が平方数}) \\ 2 & (a^2 - 4b \; \text{が平方数ではない}) \end{cases}$
$(\ker(\psi) : \ker(\psi) \cap \phi( E(\qq) ) ) = \begin{cases} 1 & (a^2 - 4b\; \text{が平方数}) \\ 2 & (a^2 - 4b\; \text{が平方数ではない}) \end{cases}$

でした。

それぞれ $a^2 - 4b$ が平方数か否かで場合分けされますが、なんと都合の良いことにいずれの場合も

$\# E(\qq)[2] \cdot (\ker(\psi) : \ker(\psi) \cap \phi( E(\qq) ) ) = 4$

となります。なんということでしょう！うまく行き過ぎています！！

結論として、次が成り立つことがわかりました。

$\displaystyle 2^r = \frac{(E(\qq) : \psi( E'(\qq) ) ) \cdot (E'(\qq) : \phi( E(\qq) ) )}{4}$

いやー、素晴らしいですね。

あとは、対称的な

$(E(\qq) : \psi( E'(\qq) ) )$
$(E'(\qq) : \phi( E(\qq) ) )$

を計算すればいいことになります。

2-descentとは (4) ：謎の準同型写像 δ, δ'

ここがもう一つの山場です。剰余群

$E(\qq) / \psi( E'(\qq) )$

の位数を決定せよ、という問題を考えます。

こういうとき非常に強力な方法がありまして、それが $E(\qq)$ からの準同型写像を考えるという方法です。準同型写像を考えて、その核が $\psi( E'(\qq) )$ に一致すれば、準同型定理により $E(\qq) / \psi( E'(\qq) )$ と準同型写像の像が同型になります。あとは像の大きさを調べてあげれば、 $E(\qq) / \psi( E'(\qq) )$ の大きさが決定できるという寸法です。

結論からいうと、次のような準同型写像 $\delta'$ を考えます：

$\begin{align} \delta' \colon E(\qq) &\longrightarrow \qq^\times / \qq^{\times 2}, \\ (x, y) & \longmapsto x \bmod{ \qq^{\times 2} }, \\ T = (0, 0) & \longmapsto b \bmod{ \qq^{\times 2} }, \\ \mathcal{O} & \longmapsto 1 \bmod{ \qq^{\times 2} } \end{align}$

なんだこれはと思ったかもしれませんが、いったん説明に付き合ってください。

まず、 $\qq^\times$ は $\qq$ の乗法群です。つまり、 $\qq - \{0\}$ を考えると、これは乗法について群をなすので、これを $\qq^\times$ と表すのです。また、 $\qq^\times$ の元を2乗してできる元全体を $\qq^{\times 2}$ と表します。すなわち、0を除く平方数全体ということですね。

$\qq^{\times 2}$ 倍を同一視してできる剰余群が $\qq^{\times }/\qq^{\times 2}$ というわけですね。したがって、代表元としては素因数分解の指数が 0 または 1 となるような数がとれます。

$\qq^{\times }/\qq^{\times 2} = \{ \prod p^{e_p} \bmod{\qq^{\times 2}} \mid e_p \in \{0, 1\}, \; \text{有限個を除いて } e_p = 0 \}$

これで写像の行き先の集合が分かりました。 $\delta'$ は $E(\qq)$ の点 $(x, y)$ のだいたい $x$ 座標をとってきて、それを $\bmod{\qq^{\times 2}}$ したもの（平方数倍の違いを無視したもの）だと思うことができます。

$\delta'$ が準同型写像であることはまったくもって自明ではありませんが、ここでは受け入れることにしましょう。（計算すればたしかに証明できます。）

ここで重要な事実としては、 $\ker(\delta') = \psi( E'(\qq) )$ であるということです。したがって、準同型定理により同型写像

$\newcommand{\im}{\operatorname{im}}\delta \colon E(\qq)/\psi( E'(\qq) ) \simeq \im(\delta') \subset \mathbb{Q}^\times / \mathbb{Q}^{\times 2}$

が得られました。

また、 $E'(\qq)/\phi( E(\qq) )$ についても全く同様に、準同型写像 $\delta$ を次のように定義します：

$\begin{align} \delta \colon E'(\qq) &\longrightarrow \qq^\times / \qq^{\times 2}, \\ (X, Y) & \longmapsto X \bmod{ \qq^{\times 2} }, \\ T' = (0, 0) & \longmapsto a^2 - 4b \bmod{ \qq^{\times 2} }, \\ \mathcal{O}' & \longmapsto 1 \bmod{ \qq^{\times 2} } \end{align}$

これにより、ランク $r$ の計算は $\# \im(\delta')$ および $\# \im(\delta)$ に帰着されることが分かります：

$\displaystyle 2^r = \frac{\# \im(\delta') \cdot \# \im(\delta)}{4}$

注：ところで、この準同型写像 $\delta, \delta'$ の由来が気になった人は多いのではないかと思います。

実は、 $\delta, \delta'$ の正体はクンマー写像と呼ばれるものです。 $\qq$ 上の楕円曲線 $E, E'$ の間の同種写像 $\phi \colon E \to E'$ は全射であることと、 $E, E', E[\phi]$ に $G_\qq$ が自然に作用することから、 $G_\qq$ 加群の短完全列

$0 \longrightarrow E[\phi] \longrightarrow E \longrightarrow E' \longrightarrow 0$

が得られます。この短完全列に対し、ガロアコホモロジーの長完全列をとると

$\delta \colon E'(\qq)/\phi( E(\qq) ) \longrightarrow H^1(\qq, E[\phi])$

なる単射が得られます。これがクンマー写像です。この写像は、長完全列を構成する際に使う「蛇の補題」の「連結準同型」になっています。

ここで、 $H^1(\qq, E[\phi]) \simeq \mathbb{Q}^\times/\mathbb{Q}^{\times 2}$ となっていて、この写像 $\delta$ を書き下したものが、まさに上の準同型になっているということです。

参考：
tsujimotter.hatenablog.com

2-descentとは (5)：im(δ') の決定

再度 $\delta'$ の定義を思い出します：

$\im(\delta')$ を決定するためには、 $E(\qq)$ の任意の点 $(x, y)$ の $x$ 座標が、 $\bmod{\qq^{\times 2}}$ でどのような値をとるのか、を考える必要があります。この辺から一気に整数論感が出てきます。

$(x, y) \in E(\qq)$ とすると、 $x, y$ は既約分数によって

$\displaystyle x = \frac{m}{e^2}, \;\; y = \frac{n}{e^3}$

と表すことができます。ここで $e > 0$ であり、既約分数より $\gcd(m, e) = 1, \; \gcd(n, e) = 1$ です。

注： $x, y$ の分母が $e^2, e^3$ になっていることについて補足します。これは

$y^2 = x^3 + \cdots$

の辺を通分したときの分母を考えて、それを割り切る任意の素数 $p$ に対して $2\operatorname{ord}_p(y) = 3\operatorname{ord}_p(x)$ が成り立つからです。

さて、ここで $y = 0$ と $y \neq 0$ で場合分けします。

(a) y = 0 のとき：

$x = 0$ のケースと $x\neq 0$ のケースがあります。

(i) x = 0 のとき：

$T = (0, 0)$ ということですから、 $\delta'(T) = b \bmod{\qq^{\times 2}}$ となります。つまり、 $b \in \im(\delta')$ ということです。

(ii) x ≠ 0 のとき：

$y = 0$ より $x^2 + ax + b = 0$ の2解が有理数であれば、その $x \bmod{\qq^{\times 2}}$ が $\delta'$ の像の要素となります。

具体的には、 $a^2 - 4b$ が平方数のとき、 $a^2 - 4b = d^2$ とおいて

$\displaystyle \frac{-a \pm d}{2}$

が $x^2 + ax + b = 0$ の2解となります。したがって、

$\displaystyle P = \left(\frac{-a + d}{2}, 0\right), \;\; \left(\frac{-a - d}{2}, 0\right) \in E(\qq)$

より

$\displaystyle \delta'(P) = \frac{-a + d}{2}, \; \frac{-a - d}{2} \bmod{\qq^{\times 2}} \in \im(\delta')$

となります。

(b) y ≠ 0 のとき（つまり、x ≠ 0 ）：

このときは、 $m \neq 0$ かつ $n \neq 0$ となります。

$x = \frac{m}{e^2}, \; y = \frac{n}{e^3}$ を $y^2 = x^3 + ax^2 + bx$ に代入すると

$\displaystyle \left(\frac{n}{e^3}\right)^2 = \left(\frac{m}{e^2}\right)^3 + a\left(\frac{m}{e^2}\right)^2 + b\left(\frac{m}{e^2}\right)$

となりますが、両辺に $e^6$ をかけると

$\displaystyle \begin{align} n^2 &= m^3 + am^2 e^2 + bme^4 \\ &= m(m^2 + am e^2 + be^4) \end{align}$

となります。ここで、 $m$ と $m^2 + am e^2 + be^4$ が互いに素であれば、左辺の $n^2$ が平方数であることから $m$ と $m^2 + am e^2 + be^4$ のどちらも平方数であることが結論づけられます。

しかし実際は、どちらも平方数であるとは限らないので、もう少し工夫します。

$b_1 = \pm \gcd(m, b)$ として、 $mb_1 > 0$ となるよう符号を選びます。すると

$m = b_1 m_1$
$b = b_1 b_2$

ただし、 $\gcd(m_1, b_2) = 1$ かつ $m_1 > 0$ とかけます。

$\gcd(m_1, b_2) = 1$ は $\gcd(b_1 m_1, b_1 b_2) = b_1$ より明らか。
$m_1 > 0$ も、 $m = b_1 m_1$ の両辺に $b_1$ をかけて、 $m b_1 = b_1^2 m_1$ であり、 $m b_1 > 0$ となるように符号を選んでいるので $b_1^2 > 0$ より言えます。

この $m = b_1 m_1, \; b = b_1 b_2$ を代入すると

$\displaystyle \begin{align} n^2 &= b_1 m_1(b_1^2 m_1^2 + ab_1 m_1 e^2 + b_1 b_2 e^4) \\ &= b_1^2 m_1(b_1 m_1^2 + a m_1 e^2 + b_2 e^4) \end{align}$

となります。

両辺を比較すると、 $b_1^2 \mid n^2$ より $b_1 \mid n$ 。よって $n = b_1 n_1$ とおくと

$\displaystyle \begin{align} n_1^2 = m_1(b_1 m_1^2 + a m_1 e^2 + b_2 e^4) \end{align}$

と表せます。

さて、ここで $\gcd(b_2, m_1) = 1$ かつ $\gcd(e, m_1) = 1$ なので、 $m_1$ と $b_1 m_1^2 + a m_1 e^2 + b_2 e^4$ は互いに素となります（やったー）。

これで、左辺が平方数より、 $m_1$ と $b_1 m_1^2 + a m_1 e^2 + b_2 e^4$ が平方数であることが結論づけられます。

$n_1 = MN$ と分解して

$M^2 = m_1$
$N^2 = b_1 m_1^2 + a m_1 e^2 + b_2 e^4$

と表すことができたわけです。

よって $m_1$ を消去して

$N^2 = b_1 M^4 + aM^2e^2 + b_2 e^4$

という式が得られました。

ここまでの変形を追いかけると、結局 $(x, y) \in E(\qq), \; y \neq 0$ を、因数分解 $b = b_1 b_2$ を用いて

$\displaystyle x = \frac{b_1 M^2}{e^2}, \;\; y = \frac{b_1 M N}{e^3}$

と表すことができるということでした。

ただし、分数の既約性より

$\gcd(b_1, e) = \gcd(M, e) = \gcd(N, e) = 1$

を満たします。また $\gcd(b_2, m_1) = 1$ より

$\gcd(b_2, M) = \gcd(M, N) = 1$

も満たします。

そして、このとき $(M, e, N)$ は関係式

$N^2 = b_1 M^4 + aM^2e^2 + b_2 e^4$

を満たすということでした。

ここで、

$\displaystyle \delta'( (x, y) ) = x = \frac{b_1 M^2}{e^2} \equiv b_1 \pmod{\qq^{\times 2}}$

となります。すなわち、 $b_1 \bmod{\qq^{\times 2}} \in \im(\delta')$ ということです。

いまの (b) のケースで言えたことを再度まとめます。

$(x, y) \in E(\qq)$ （ $y\neq 0$ ）が与えられたとき、因数分解 $b = b_1 b_2$ を用いて

条件（☆）

$M \neq 0$
$\gcd(b_1, e) = \gcd(M, e) = \gcd(N, e) = 1$
$\gcd(b_2, M) = \gcd(M, N) = 1$
$N^2 = b_1 M^4 + aM^2e^2 + b_2 e^4$

を満たす $(M, e, N)$ によって、 $x = \frac{b_1 M^2}{e^2}, \;\; y = \frac{b_1 M N}{e^3}$ と表せるということでした。

逆に、ある因数分解 $b = b_1 b_2$ に対して、条件（☆）を満たす整数 $(M, e, N)$ の組があったとしましょう。

$N^2 = b_1 M^4 + aM^2e^2 + b_2 e^4$

の両辺に $\frac{b_1^2 M^2}{e^6}$ をかけると

$\displaystyle \left(\frac{b_1 MN}{e^3}\right)^2 = \left(\frac{b_1 M^2}{e^2}\right)^3 + a\left(\frac{b_1 M^2}{e^2}\right)^2 + b_1 b_2 \left(\frac{b_1 M^2}{e^2}\right)$

となります。 $x = \frac{b_1 M^2}{e^2}, \;\; y = \frac{b_1 M N}{e^3}$ とおくと、 $(x, y) \in E(\mathbb{Q})$ であることがわかります。

なお、このとき $M \neq 0$ （つまり $x\neq 0$ ）ですが、 $N \neq 0$ とは限らないため $y = 0$ になることもあります。このときは、場合分け (a)-(ii) の解が得られたことになります。

2-descentとは (6)：結論

長かったですが、以上の事実によって我々は楕円曲線 $E, E'$ の有理点のランクを決定するための手段を得たことになります。

まず、有理点のランク

$r = \rank E(\mathbb{Q}) = \rank E'(\mathbb{Q})$

は、次の公式で計算できます：

$\displaystyle 2^r = \frac{\# \im(\delta') \cdot \# \im(\delta)}{4}$

$\delta, \delta'$ は前々節で定義した準同型写像です。これらの像は具体的に次のように得られます：

$\im(\delta')$ の計算方法

$\im(\delta')$ は次の集合 $U_1, U_2, U_3$ の合併として得られる $\qq^\times/\qq^{\times 2}$ の部分群である：

$U_1 = \{1 \bmod{\qq^{\times 2}} \}$
$U_2 = \{b \bmod{\qq^{\times 2}} \}$
$U_3 = \{ b_1 \bmod{\qq^{\times 2}} \mid b = b_1 b_2 \; \; \text{s.t 条件（☆）を満たす整数の3つ組 } (M, e, N) \text{ が存在する} \; \}$

条件（☆）を以下に再掲します：

条件（☆）

$M \neq 0$
$\gcd(b_1, e) = \gcd(M, e) = \gcd(N, e) = 1$
$\gcd(b_2, M) = \gcd(M, N) = 1$
$N^2 = b_1 M^4 + aM^2e^2 + b_2 e^4$

$\im(\delta)$ についても、 $E$ を $E'$ におきかえて（係数 $a, b$ を $-2a,\; a^2 - 4b$ に置き換えて）そのまま実行することで計算できます。

例１： E: y² = x³ - x, E': Y² = X³ + 4X の場合

それでは、いよいよ冒頭の $E\colon y^2 = x^3 - x$ のランクを計算しましょう。

2つの楕円曲線

$E = y^2 = x^3 - x$
$E' = Y^2 = X^3 + 4X$

とその間の同種写像

$\phi \colon E \longrightarrow E', \; (x, y) \longmapsto (y^2/x^2, \;\; y(x^2+1)/x^2)$
$\psi \colon E' \longrightarrow E, \; (X, Y) \longmapsto (Y^2/4X^2, \;\; Y(X^2-4)/8X^2)$

をそれぞれ与えます。

前々節で定義した準同型写像

$\delta' \colon E(\qq) \longrightarrow \qq^\times / \qq^{\times 2}$
$\delta \colon E'(\qq) \longrightarrow \qq^\times / \qq^{\times 2}$

について、 $\im(\delta'), \; \im(\delta)$ を計算し、公式

$\displaystyle 2^r = \frac{\# \im(\delta') \cdot \# \im(\delta)}{4}$

によって、ランク $r = \rank E(\mathbb{Q}) = \rank E'(\mathbb{Q})$ を決定したいと思います。

#im(δ') の計算：

$E\colon y^2 = x^3 - x$ の係数は $a = 0, \; b = -1$ なので、 $b$ の約数 $b_1$ が $\# \im(\delta')$ の候補となります。

$b = -1$ の約数は $1, -1$ なので、 $b = b_1 b_2$ としたとき

$b_1 = 1, \; \; b_2 = -1$

$b_1 = -1, \; \; b_2 = 1$

の $b_1$ が候補となります。（この時点では全部が $\im(\delta')$ に入っているとは限りません。）

ここで、定義から $\delta(\mathcal{O}) = 1$ なので、 $1 \in \im(\delta')$ であることは分かります。

また、これまた定義から $\delta(T) = b = -1$ なので、 $-1 \in \im(\delta')$ であることも分かります。

したがって、

$\im(\delta) = \{ 1, -1 \bmod{\qq^{\times 2}}\}$

であることが分かりました。よって、 $\# \im(\delta) = 2$ です。

今回は非常に簡単でしたね。

#im(δ) の計算：

$E'\colon y^2 = x^3 + 4x$ の係数は $a = 0, \; b = 4$ なので、 $b$ の約数 $b_1$ が $\# \im(\delta)$ の候補となります。

$b = 4$ の約数は $1, -1, 2, -2, 4, -4$ なので、、 $b = b_1 b_2$ としたとき

① $b_1 = 1, \; \; b_2 = 4$

② $b_1 = -1, \; \; b_2 = -4$

③ $b_1 = 2, \; \; b_2 = 2$

④ $b_1 = -2, \; \; b_2 = -2$

⑤ $b_1 = 4, \; \; b_2 = 1$

⑥ $b_1 = -4, \; \; b_2 = -1$

の $b_1$ が候補となります。こっちはパターンが多そうですが、いくつかの候補はただちに削ることができます。

まず、 $\im(\mathcal{O}') = 1$ なので、 $1 \in \im(\delta)$ です。よって、候補①は検討する必要はありません。

また、平方数倍を考慮すると

$1 \equiv 4 \bmod{\qq^{\times 2}}$

$-1 \equiv -4 \bmod{\qq^{\times 2}}$

なので、①と⑤、②と⑥はどちらかを考えれば十分です。①は既に検討しているので⑤を消去し、②をこのあと検討することにして⑥も消去しておきましょう。

ゆえに、考えるべき選択肢は②・③・④のみです。

② $b_1 = -1, \; \; b_2 = -4$

③ $b_1 = 2, \; \; b_2 = 2$

④ $b_1 = -2, \; \; b_2 = -2$

これらの候補に対して

$N^2 = b_1 M^4 + aM^2e^2 + b_2 e^4$

なる整数の組 $(M, e, N)$ を探しましょう。

もし条件（☆）を満たす整数解が１つでもあれば $b_1 \in \im(\delta)$
もし条件（☆）を満たす整数解が１つもなければ $b_1 \not\in \im(\delta)$

となります。これで完全に整数論の問題に落ちましたね。

$a = 0$ であることに注意しつつ、 $b_1, b_2$ を代入していくと

② $N^2 = -M^4 - 4e^4$

③ $N^2 = 2M^4 + 2e^4$

④ $N^2 = -2M^4 - 24e^4$

となります。これらが整数解を持つか考えましょう。

実は、左辺を考えると $N^2 \geq 0$ なので、右辺も 0 以上でなければなりません。一方、②と④は符号がすべて負になっており、 $M^4, e^4 \geq 0$ です。特に $M \neq 0$ なので、どうやっても右辺は 0 以上にはなりません。したがって、 $-1, -2 \in \im(\delta)$ であることがわかります。

こんな風にただちに判断できるケースもあるのですね。一般に $b$ が正の場合は、 $b_1 < 0$ ならば $b_2 < 0$ なので、 $a = 0$ のとき方程式に解はありません。次からはこのようなケースは検討する必要がないということですね。

最後に残ったのは③ですが、これは地道に考えましょう。実際、 $(M, e, N) = (1, 1, 2)$ とすると

$2^2 = 2\cdot 1^4 + 2\cdot 1^4$

なので、方程式③を満たします。条件（☆）における最大公約数の条件もクリアします。

したがって、 $\im(\delta)$ が次のように決定できました：

$\im(\delta) = \{ 1, 2 \bmod{\qq^{\times 2}} \}$

よって、 $\# \im(\delta) = 2$ です。

ランク r の決定と E(ℚ) の決定：

以上により、 $\# \im(\delta') = 2, \;\; \# \im(\delta) = 2$ であることが分かったので、公式より

$\displaystyle 2^r = \frac{\# \im(\delta') \cdot \# \im(\delta)}{4} = \frac{2\cdot 2}{4} = 1$

となり、ランクは

$r = \rank E(\qq) = \rank E'(\qq) = 0$

であることが分かりました。

つまり、 $E(\qq)$ に無限位数の点は存在しないということが証明されたわけですね！

せっかくなので、 $E(\qq)$ の構造も特定しましょう。 $\rank = 0$ なので、あとは位数有限の点だけ考えれば十分です。

ここで、Nagell-Lutzの定理より、位数有限の点 $(x, y) \in E(\qq)$ であれば、その $y$ 座標は

$y = 0$
$y \mid \Delta$ （ $\Delta$ は $E$ の判別式）

となります。判別式は $\Delta = 4$ なので、 $y$ の候補は $y = 0, \; \pm 1, \; \pm 2, \; \pm 4$ です。

ここで、 $y = 0$ のとき $x = 0, 1, -1$ となります。

$y \neq 0$ のとき、 $x^3 - x - y^2$ は整係数のモニック多項式なので、その根 $x$ は整数になります。実際、計算してみると整数にはならないので、有理点ではありません。

ゆえに、

$E(\qq) = \{ \mathcal{O}, \; T = (0, 0), \; (1, 0), \; (-1, 0) \}$

ということが分かりました。

応用：1は合同数ではない

せっかくなので、合同数との関係について紹介しましょう。

自然数 $n$ に対して楕円曲線 $E_n\colon y^2 = x^3 - n^2 x$ を考えます。これは $n$ が合同数かどうかに深く関係していて、特に次の必要十分条件が成り立ちます：

$\rank E_n(\qq) > 0 \;\; \Longleftrightarrow \;\; n \; \text{は合同数}$

注：詳細はこちらの記事を読んでください：
tsujimotter.hatenablog.com

$E_1$ が先ほど計算した $E\colon y^2 = x^3 - x$ なので、 $\rank E_1(\qq) = 0$ より、 $1$ は合同数ではないことが導けます。面白いですね！

実際、合同数ではないことを示すのは非常に難しいのですが（合同数であることを示す方が幾分簡単）、ランクを決定できれば合同数かどうかの判定ができてしまうというお話でした。

応用：フェルマーの最終定理（n = 4 のとき）

楕円曲線 $E\colon y^2 = x^3 - x$ の有理点は、実は $n = 4$ のときのフェルマーの最終定理に関係しています。

$n = 4$ のフェルマーの最終定理

$X^4 + Y^4 = Z^4$ は自然数解を持たない

実は、 $E(\qq) = \{ \mathcal{O}, \; T = (0, 0), \; (1, 0), \; (-1, 0) \}$ であることから（特に $y\neq 0$ なる有理点が存在しないことから）、上記が従うのです。

ここで、

「 $N^4 = e^4 + M^4$ なる自然数解 $(M, e, N)$ が存在する」

と仮定しましょう。

このとき、本記事の中盤で議論したものと同じ手順で $E$ の有理点を構成できます。

まず、

$N^4 = M^4 - e^4$

と変形します。 $e \neq 0$ より両辺に $M^2/e^6$ をかけると

$\displaystyle \left(\frac{MN^2}{e^3}\right)^2 = \left(\frac{M^2}{e^2}\right)^3 - \left(\frac{M^2}{e^2}\right)$

となり、 $x = \frac{M^2}{e^2}, \;\; y = \frac{MN^2}{e^3}$ とおくと、 $y^2 = x^3 - x$ を満たします。

$N\neq 0$ より、 $y \neq 0$ です。したがって、 $y \neq 0$ なる $E(\qq)$ の有理点 $(x, y)$ が構成されました。

一方、 $E(\qq)$ には $y \neq 0$ なる有理点は $\mathcal{O}$ 以外なく、矛盾します。したがって

「 $N^4 = e^4 + M^4$ なる自然数解 $(M, e, N)$ が存在する」

という仮定が誤りと分かり、ここから $n = 4$ のフェルマーの最終定理が従います。

$n = 4$ のフェルマーの最終定理の別証明が得られるというのは、面白いですね！

例２： E: y² = x³ - 5x, E': Y² = X³ + 20X の場合

最後に、ランクが 0 ではないケースについても計算してみましょう。

2つの楕円曲線

$E = y^2 = x^3 - 5x$
$E' = Y^2 = X^3 + 20X$

とその間の同種写像

$\phi \colon E \longrightarrow E', \; (x, y) \longmapsto (y^2/x^2, \;\; y(x^2+5)/x^2)$
$\psi \colon E' \longrightarrow E, \; (X, Y) \longmapsto (Y^2/4X^2, \;\; Y(X^2-20)/8X^2)$

をそれぞれ与えます。

これらに対して、 $\im(\delta'), \; \im(\delta)$ を計算し、ランクを決定してみましょう。

#im(δ') の計算：

$E\colon y^2 = x^3 - 5x$ の係数は $a = 0, \; b = -5$ なので、 $b = -5$ の約数 $\pm 1, \; \pm 5$ が $\im(\delta')$ の候補となります。

ここで、 $\delta'(\mathcal{O}) = 1$ と $\delta'(T) = b = -5$ なので、 $b = b_1 b_2$ として

① $b_1 = -1, \;\; b_2 = 5$

② $b_1 = 5, \;\; b_2 = -1$

の2通りを考えればよいでしょう。

ところが、上記の①②に対応する方程式は

① $N^2 = -M^4 + 5e^4$

② $N^2 = 5M^4 - e^4$

ですが、これらは $M, e$ の入れ替えに対して対称的です。したがって、①だけ考えれば十分です。

①に対しては、 $2^2 = -1^4 + 5\cdot 1^4$ という解がありますので、 $-1, 5 \in \im(\delta')$ です。

以上により、候補すべてが $\im(\delta')$ の元であることが分かりました。よって

$\im(\delta') = \{ 1, -1, 5, -5 \bmod{\qq^{\times 2}}\}, \;\; \;\; \#\im(\delta') = 4$

ということになります。

#im(δ) の計算：

一方、 $E'\colon Y^2 = X^3 + 20X$ の係数は $a = 0, \; b = 20$ なので、 $b = 20$ の約数が候補となります。しかしこれは多いですね。

楽をするために、 $b = 20 > 0$ であることに着目すると、因数分解 $b = b_1 b_2$ が $b_1 < 0$ のとき $b_2 < 0$ となります。このとき

$N^2 = b_1 M^4 + b_2 e^4$

は左辺が 0 以上であり、 $M\neq 0$ で右辺が常に負の値をとるため所望の整数解を持ちません。したがって、 $b$ の約数としては正のものだけ考えればよいです。

$b$ の正の約数は $1, 2, 4, 5, 10, 20$ の6通りですが、もう少しだけ候補を減らせます。

$\delta(\mathcal{O}') = 1, \;\; \delta(T') = b = 20$ なので、 $1, 20 \in \im(\delta)$ です。また、 $1\equiv 4 \bmod{\qq^{\times 2}}$ なので、 $4$ は考える必要がありません。また、 $5 \equiv 20 \bmod{\qq^{\times 2}}$ も同様です。