1つ前の記事で「合同数」の話が出たので,合同数についてのもう一つの話題を。
復習しておくと,合同数とは「すべての辺の長さが有理数であるような直角三角形の面積になる数」のことです。
図で表すとわかりやすいですね。

前回述べたように,合同数の例としては, が挙げられます。辺の長さが
である直角三角形を考えると,
が成り立ち,また面積は,
より,たしかに が合同数であることがわかります。
このように都合のよい辺の長さが見つかれば別ですが,一般に与えられた に対して,
が合同数であることを示すのは困難です。
タイトルの 「7は合同数」 を初めて示したのはあのオイラーです。
「またお前か」って感じですよね。笑
合同数は,古代ギリシアやアラビア時代から考えられていたテーマのはずですが,「7は合同数かどうか」というかなり特殊な設定の問題ですら,オイラーまで解決していなかったというのは驚きですね。
さて,お待ちかねの「7は合同数」であることを示す直角三角形はこちらです。
じゃじゃーん!

えぇーっと・・・。まじかー・・・。って感じですよね。笑
念のため検算しましょう。
とおきます。
が成り立っていますね。さらに,
となって,たしかに は合同数です。*1
合同数探しは,現代においてはもう少し状況はマシになっています。たとえば,「Tunnell(タネル)の定理」という定理があって,これは合同数の必要十分条件ではないものの,合同数の特徴づけに役に立ちます。
定理(Tunnell, 1983):
を平方因子を持たない正の奇数とする.このとき,
ならば
が成り立つ.

は合同数.

を満たす整数の3つ組
の数は,
を満たす整数の3つ組
の数の2倍に等しい.
また,弱バーチ−スウィナートン・ダイアー(Birch−Swinnerton-Dyer: BSD)予想が正しいとき,
ならば
が成り立つ.
逆が成り立てば大いにすっきりするわけですが,BSD予想は楕円曲線における超有名な未解決問題ですから,なかなか一筋縄ではいかなそうですね。
楕円曲線といえば,合同数は楕円曲線にも関係するそうです。
が合同数である条件は,
かつ
となるような有理数 が存在することです。
ここで, とおくと,
のような楕円曲線 が得られます。
変数の置き方から考えて, の有理点は必ずしも合同数の条件と一致しませんが,この関係によって「合同数の問題」を「楕円曲線の枠内」で捉えることができそうです。
最後に,Don Zagier が例として用いた「とんでもない直角三角形」をご紹介して終わりにしましょう。
これが,有理数の辺の長さを持ち面積が となる 最も単純な 直角三角形です。
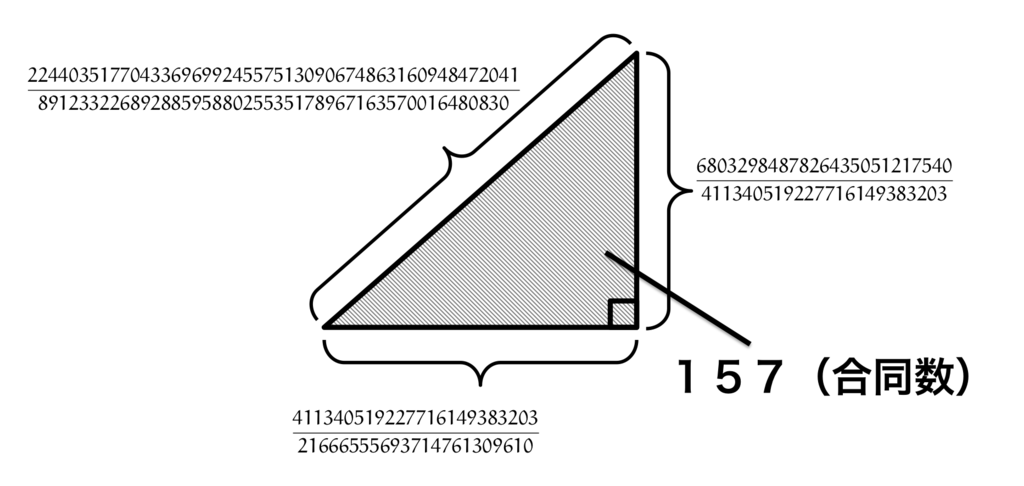
これが最も単純な例なのだそうです。とんでもないですね。
確認したい人向けに,テキストも用意しました。どうぞ計算にお使いください。笑
この例は,N. コブリッツの「楕円曲線と保型形式」を見て知ったのですが,さすがに入力ミスの可能性が高かったので,以下の PDF からコピペしました。だから,間違いはないと思います。たぶん。
Shou-Wu Zhang - Congruent Numbers and Heegner Points
http://www.asiapacific-mathnews.com/03/0302/0012_0015.pdf
ってこの記事自体(というか後半の Tian の論文*2)もなかなかすごいこと言っているんじゃないの!?
と興味は尽きないですね。
それでは今日はこの辺で。
*1:この例はこちらの PDF からとってきました。 http://mathematics-pdf.com/pdf/congruent_number.pdf
