ゼータ関数強化月間 第2弾 として,今日は
を紹介したいと思います。
デデキントのゼータ関数によって「類数」が求まる 「類数公式」 についてお話したいと思います。
証明の流れが非常に面白いので,そのあたりを楽しんでいただければと思います。
類数とは
そもそも「類数」とはなんだったか。簡単に復習したいと思います。
類数とは,イデアル類群という特別な群の位数のことです。イデアル類群は,イデアルのバリエーションがどれぐらいあるか,どれぐらい複雑に絡み合っているのかを示す群です。
有理数体の整数環,すなわち「整数」の世界では「素因数分解の一意性」が成り立ちますが,一般の代数体においてはそうとは限りません。有理数体に という数を添加しただけの「二次体」においても,その整数環は一般に素因数分解の一意性が成り立ちません。
この問題に対して,クンマーという数学者は「イデアル」を使って一意性を回復する解決策を編み出しました。数をイデアルまでもっていけば,「素イデアル分解」という形で一意性が復活するのです。
一方で,素イデアル分解は「単項イデアル」だけでは実現しません。分解の法則は,単項イデアル以外のイデアルによっても左右されるため,これらがどの程度含まれるかが興味の対象になります。この「単項イデアル以外のイデアルの類がどれだけあるか」という情報を持った群が,イデアル類群なのです。
要するに,イデアル類群の位数が大きければ,それだけ通常の数の世界から遠いということです。その度合いを「類数」を通して測りたいというわけです。
イデアルやイデアル類群については,以下の記事でまとめています。詳しく知りたい方はぜひ読んでみてください。
Z[√-5] のイデアルについて - tsujimotterのノートブック
二次体 Q(√-5) のイデアル類群と xx + 5yy 型の二次形式 - tsujimotterのノートブック
さて,代数体のことを調べたい我々にとっては,この類数はとても重要で,どうにか理解したい量でもあります。ところが,この類数というものはつかみどころのない対象で,一筋縄では法則を見出すことができません。
そんな類数について調べることができる公式が,今回紹介する「類数公式」です。
ディリクレの類数公式
イデアル類群や類数は,先に述べた通り代数体に対して定義された,純粋に「代数的」な量といえます。
一方でディリクレは,類数が 関数という「解析的」な関数で計算できることを示しました。
実際,以下のような定理が成り立ちます。
このとき判別式の符号に応じて, の類数
が以下で計算できる。
のとき(虚二次体):
のとき(実二次体):
二次体の類数 が,
という関数によって計算できるというものです。
以下では,定義が不明瞭な部分について解説していきましょう。
まず, は
関数と呼ばれる関数で,以下のようにリーマン・ゼータ関数にそっくりの級数の形で定義されます。
この関数については,あとでいくつか例を計算してみましょう。
一般の 関数の定義としては,
にはディリクレ指標と呼ばれる指標(
から
への写像)が入ることになります。
類数公式においては, として クロネッカーの記号 を用います。クロネッカーの記号はディリクレ指標の一種です。二次体
に対して一意に定まるので「二次体に付随する指標」と呼びます。
具体的には,以下のように定義されます。少々ややこしい定義となっています。
の素因子が
を割り切るとき:
と
が互いに素のとき:
ただし, はヤコビ記号で,
と素因数分解したとき
と定義される。
奇素数 に対する
はルジャンドル記号で,
が
の平方剰余のとき
,平方非剰余のとき
となる。
に対する
は,特別に以下で定義する:
クロネッカーの指標は,私のブログでも何度も登場している記号です。頻繁に登場する割に定義が複雑なので,毎度この記号を説明するのに苦労します。
簡単に言ってしまうと「平方剰余記号」のようなものです。「二次体に付随する指標」の名の通り,この記号を用いると二次体の分解法則がわかりやすく説明できます。
具体的には,二次体の分解法則は以下のようになります:
のとき,
は
で完全分解
のとき,
は
で惰性する
のとき,
は
で分岐する
まさに,二次体の分解法則を司っている指標といえますね。以上の性質は,後ほど類数公式の証明で使います。
もう一つ覚えて欲しい重要な性質があります。定義上は は
を変数とする関数のように見えて,実際のところ
で値が定まる関数になっているという点です。この性質はクロネッカーの記号を計算する上で便利です。
tsujimotter.hatenablog.com
もう一つ,単数についても触れておきましょう。
単数とは,整数環における乗法的な可逆元のことです。二次体の整数環においては,ノルムが の元に一致します。
二次体における単数は,虚二次体と実二次体で扱いが大きく異なります。簡単に言うと,虚二次体の単数は有限個で,実二次体の単数は無数に存在します。
虚二次体の単数は有限個なので,その数を と定めることができます。
実は以上の2つが例外で,あとの虚二次体については単数は の
つだけとなります。したがって,一般に
となります。
一方,実二次体の単数は,もっとややこしくなります。実二次体の単数は,ペル方程式と呼ばれる方程式の整数解を使って表現されますが,このような解は無数に存在します。類数公式に現れた「基本単数 」とは,このような単数の中で最も小さいもののことです。
単数が多いとそれだけ問題が大変になります。類数公式の証明で「イデアルの個数」と「整数の個数」を数えることになるのですが,単数の数が多いと,両者の大きさにずれが生じます。そのあたりの事情が類数公式にも関わってきます。
単数をかけてできる数を「同伴数」といいます。同伴数の分だけ「イデアルの個数」よりも「整数の個数」の方が増えてしまいます。「整数の個数」は「イデアルの個数」のちょうど単数倍となるのです。
「整数の個数」を使って「イデアルの個数」を数える際は,以上の効果を加味して「単数(同伴数)の個数」で割ってあげる必要があります。
最後に「デデキントのゼータ関数はどこいった?」と思ったかもしれませんが,デデキントのゼータ関数の定義と類数公式との関係については,後に証明の中で述べていこうと思います。
定義の説明は以上です。何はともあれ,まずは具体例を計算してみましょう。
類数の求め方の例1( の場合):
の場合):
を
の指標とすると,
となります。したがって, 函数は
のように書けます。これはいわゆるライプニッツの公式というやつですね。
たとえライプニッツの公式を知らなかったとしても,類数の計算に支障はありません。 関数の定義式を数値的に計算すればよいのです。
を十分大きい正の整数として
ですから, と
を代入して,
を計算してみましょう。
計算結果を以下のグラフに表します。横軸は和の項数 で,縦軸は和
の値です。
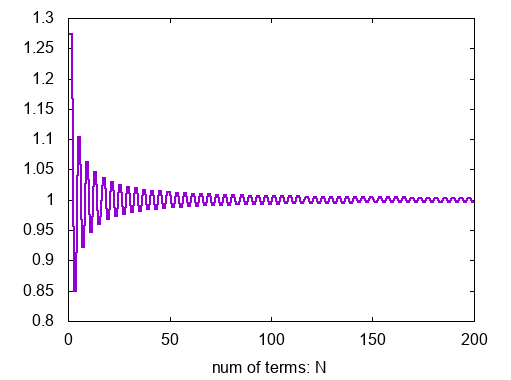
明らかに に収束することが見て取れます。したがって類数は
です。
類数は正の整数値しかとりませんので,無限級数の計算を途中で打ち切っても類数は十分にわかってしまうのですね。
類数の求め方の例2( の場合):
の場合):
類数が 以上のケースも考えてみましょう。
上の例と違って,虚二次体 に付随する指標
についての
関数の公式なんて知らないですね。こんな場合でも類数は計算できるのです。
まず, は平方剰余の相互法則より
で以下のように定まります。
と
を代入して,
を計算してみましょう。
同様に計算結果を以下のグラフに表します。横軸は和の項数 で,縦軸は
項目までの和です。
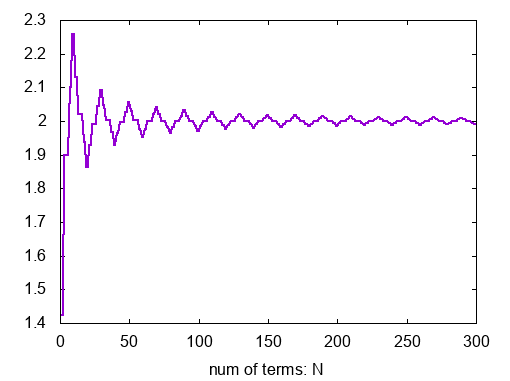
今度は,和が に収束することがわかります。したがって,類数は
であることがわかります。
こんな風に計算することができます。類数公式,素晴らしいですね。
類数公式の証明
ここから先は,類数公式の証明をしていきたいと思います。
証明の概略は高木先生の「初等整数論講義」に載っていました。今回はこちらの内容をご紹介したいと思います。

- 作者:高木 貞治
- 発売日: 1971/10/15
- メディア: 単行本
まずは,簡単に証明のポイントと方針を紹介します。
証明では「代数的な考察」と「幾何的な考察」と「解析的な考察」という三つの異なる柱が必要となります。
「代数」「幾何」「解析」とは,いわゆる数学の三大分野と呼ばれるものですが,これらの異なる分野の考え方を横断的に用いるところに,今回の証明の面白さがあります。
とはいえ,イデアルのそれぞれの類は無限に元をもっていますから,単に数を数えるだけではダメです。
どう考えるかというと,ノルムが 以下となるようなイデアルの個数に限定するのです。そうすることで,個数が有限個になりますので,先の議論が成り立ちます。あとは,そのノルムの上限
を無限大に飛ばしてあげればよいのです。
幾何的な考察では,イデアルの個数を数える問題を,楕円内に含まれる格子点の個数を数える問題に帰着させます。さらに, の極限であれば「楕円の面積」でそれが求まることを示します。これによって,類数公式の右辺にある円周率
などが出てきます。
解析的な考察では,イデアルの個数を「デデキントのゼータ関数」によって数えます。デデキントのゼータ関数には,ノルムを固定したイデアルの個数の情報が含まれており,これにより先の幾何的な考察によって得られた式と結びつきます。デデキントのゼータ関数は,一般の代数体で考えられるものですが,これを二次体に限定すると,自然に 関数が現れます。
このようにして「類数」と「 関数」が結びつくという不思議な公式が得られるのです。
証明について 3点 注意があります。
1つめは,今回の証明は厳密ではないということです。つまり,解析的な関数を取り扱いますが,その関数の連続性や収束性について厳密に議論しません。類数と関数が関連する仕組みを説明するにとどめます。
2つめは,今回の証明は虚二次体に限定したものとなっています。先ほど述べた通り,実二次体では単数が無数に存在します。したがって,単数をかけるといくらでも同じノルムを持つ数を作れてしまうわけです。これを適切に数え上げるためにやや面倒な議論が挿入されます。話の流れが悪くなるので,今回は省略したいと思います(初等整数論講義には,実二次体の証明も載っています)。
3つめは,虚二次体の中でも, は例外として除いています。これまた同伴数の問題ですが,前者は
の
つが単数となり,後者では
の
つが単数となります。一方で,それ以外の虚二次体では,単数は
の
つだけです。いちいち場合分けするのが面倒なので,上記2つの例外を除いて
として進めます。 実際の証明の流れはほとんど変わりません。
それでは,少し長いですが証明にチャレンジしましょう。
代数的な考察:イデアルの個数を数える
今,数えたいイデアルの「類」に属する任意のイデアルを とおきます。このなかで
となる
の個数を
とします。この個数を数えるのが,ここから先の目標となります。
また, の含まれる「類」に対して,逆にあたる「類」を考え,この「類」からイデアル
を1つとって固定します。
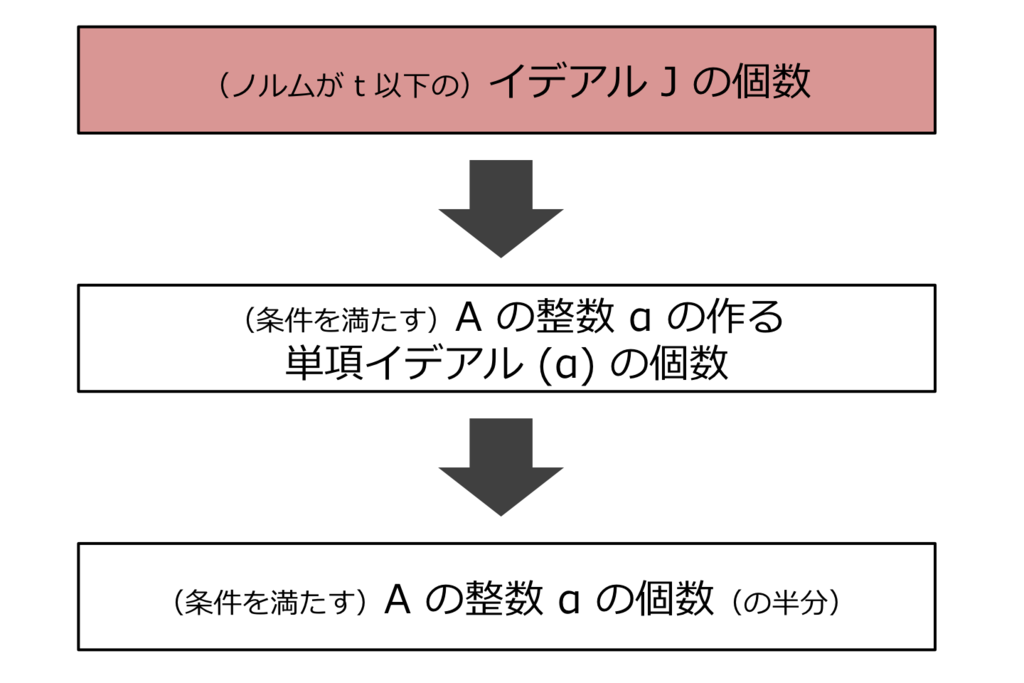
任意の に対して,
は単項イデアルの類に属します(図参照)。

ようするに, に対して
がただ一つ定まりますね。このとき
になります。
逆に, を
に含まれる
なる整数とします。
として
は数えたい類に属します。すなわち,
に対して
がただ一つ定まりますね。
以上の考察から,「 の個数を数える」ということは,固定した
の中の整数
を考えて「(
の生成する)単項イデアル
の個数を数える」ことに他なりません。
また,「単項イデアル の個数を数える」ということは「(同伴数を除いて)整数
の個数を数える」ということです。
結局のところ, を満たす
の個数
を数えるためには
を満たす の個数を数えて,単数の個数で割ってあげればよいとわかります。
仮定より,虚二次体の単数は の2つが存在します。したがって,式
の不等式を満たす
は,ちょうど
個あることがわかります。
ここで の個数を数える方向にシフトするわけです。このためには,そもそも
の持つ
をうまく表現しておく必要があります(そうしておかないと数えづらい)。
は任意に選べるので原始的イデアルとしておきます。すると,
は標準的な底によって表すことができます。つまり,
ということです。ここで は,虚二次体の判別式
を使って
と表されます。 は
に対して一意に定まる有理整数で,とくに
です。
以上のように設定すると, は有理整数
を使って
と表すことができます。このような に対して,式
の条件を満たすものを探せばよいですね。
また, のノルムを計算しておきましょう。
としておきます。
ここで,これを とおいておきます。すると,係数の比較から
です。また,
であるから,
となります。
以上の話をまとめて,条件 を置き換えましょう。
を使うと
より
と置き換わります。
すなわち,式 を満たす格子点
の個数が,求める
であることがわかります。
以上により,ノルムが 以下のイデアルの個数
を,二次形式の不等式の条件に帰着させることができました。
あとは,このような不等式を満たす格子点の個数を数えればよいのです。そこで使えるのが「幾何学的」な考え方です。
ここで となって,二次形式の判別式が二次体の判別式に一致することを覚えておいてください。あとでわかるのですが,格子点の個数を数えるのに,
の具体的な値は必要ないのです。
幾何的な考察:楕円の面積に帰着する
以下では,先の不等式の条件を幾何学的に捉えて,格子点の個数を数えたいと思います。
まず,
という式は,楕円を表す方程式だという点から確認しましょう。
この事実を理解するためには,線形代数で登場する「主軸変換」を思い出す必要があります。
とできる。
内側の行列を として
と対角化する。
は
の固有値である。
と回転しておくと,
となる。
これは,円を 方向に
倍,
方向に
倍した楕円である。
基底を回転行列 で回転させたので,これを
で逆方向に回転させたものが元の楕円である。
以上が,主軸変換でしたね。
さて,元の不等式は,
でした。これに の点を加えると(左辺の不等式に等号を含めると)
となって,このような格子点 の個数は
となります。実は,こうしておいたほうが後々計算しやすくなるのです。
次に,全体を 倍してみましょう。すると,
を満たす,サイズ の格子点の個数が
となります。
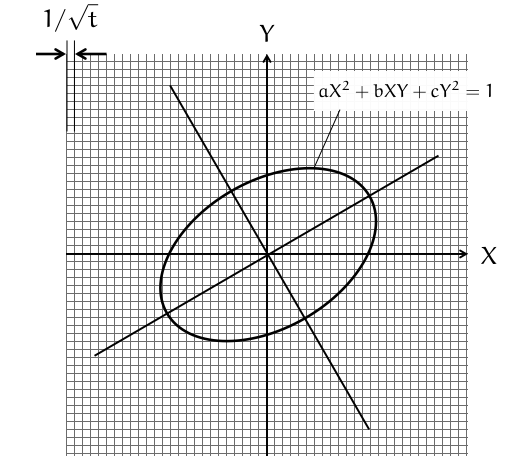
格子のつくる正方形の面積はすべて等しいので,格子点の数を数えれば楕円の面積が近似的に求まります。すなわち,
ということです。
に飛ばせば,両辺は厳密に一致します。つまり
が成り立つということです。
したがって,条件を満たす格子点の個数を「楕円の面積」に帰着することができました。
楕円の面積は,主軸変換によって保たれます。したがって,
と表される楕円の面積を計算すればよいわけです。ここで, は行列
の固有値とします。
実際に計算すると,楕円の面積は
と求まります。ここで, で,さらに
より
とすることができます。
おお,判別式が出てきました!きれいな式にまとまりましたね!
先ほど注意したように,二次形式で表される楕円の面積は の値によらず,判別式のみで決定されることがわかりました。しかも,二次形式の判別式は,元々の二次体
の判別式そのものですね。
さて,この楕円の面積が,格子点の個数と一致するので
が得られることがわかります。少し計算すると
が成り立ちます。
以上の結果は,単純に二次体の判別式のみに依存していて,イデアルの「類」の選び方によらないことに注意しましょう。
ここまで任意に一つの「類」を選んで,その「類」に属するイデアルのノルムに対する密度を計算してきました。それぞれの「類」のノルム密度は,イデアルの「類」の選び方によらないことがわかりました。
したがって, なるイデアルの総数を
とすると,
は「各類に属するイデアルの個数」と「類数」の積で表せることがわかります。すなわち,類数を
として
が成り立つということです。よって,ノルム密度を計算すると
が成り立ちます。
いったんまとめましょう。
ただし, とする。
は
の同伴数の個数。
ここまで,「代数」と「幾何」の道具を使って,ノルムが 以下のイデアルの密度を類数に結びつけることができました。
とはいえ,我々の目標は類数を計算することです。イデアルのノルム密度 は,そのままでは簡単に計算することはできません。したがって,ノルム密度を異なる方法で計算する必要があります。
そこで使えるのが「解析」の道具,すなわちゼータ関数です。ようやく本日のもう1つの主役の登場です。
解析的な考察:デデキントのゼータ関数
さて,解析的な考察の主役になるのは,デデキントのゼータ関数です。この関数を使うと,果たしてどのようにイデアルのノルム密度が計算できるのでしょうか。
まずは,定義を見てみましょう。
和の は
の
でないすべてのイデアルを渡る.
以上の級数は, で収束します。
デデキントのゼータ関数は,イデアルの個数を考えるためのよい道具です。イデアルの個数を数えるという視点で, となるような項をまとめてみると
となります。ただし,ここで は
を満たすイデアルの個数です。
求めたいのは なるイデアルの個数
ですから,
が計算できればいいですね。
それでは,この問題を考えるための解析的な準備をしていきましょう。
まず,ゼータ関数といえばオイラー積を考えるのが定石です。デデキントのゼータ関数にもオイラー積は存在します。
ノルム写像は完全乗法的なので,リーマンのゼータ関数と同様に以下が成り立ちます。
tsujimotter.hatenablog.com
さて,ここで を二次体に限定すると「二次体の分解法則」により,オイラー積をさらに変形できることがわかります。
まず,冒頭で述べたように,二次体の有理素数はクロネッカーの指標 を使って「(i) 完全分解」「(ii) 惰性」「(iii) 分岐」の3種類に分類されます。それぞれのケースに合わせて,以下のように記号を設定しましょう。
(i) 完全分解
素イデアル に完全分解する有理素数を
とすると,以下が成り立つ:
| 分解法則 | ノルム | クロネッカーの指標 |
|---|---|---|
(ii) 惰性
素イデアル に惰性する有理素数を
とすると,以下が成り立つ:
| 分解法則 | ノルム | クロネッカーの指標 |
|---|---|---|
(iii) 分岐
素イデアル に惰性する有理素数を
とすると,以下が成り立つ:
| 分解法則 | ノルム | クロネッカーの指標 |
|---|---|---|
以上の設定を用いると,オイラー積は以下のように変形できます:
ここで, は同じノルム
に一致すること(つまり,重複して数えられるということ),
と
,
と
はそれぞれ1対1に対応することを考慮すると,上記の無限積は有理素数
によって書き換えることができます。
さて,上記に現れた有理素数 は,すべての有理素数を尽くしています。したがって,最後の式の左側のカッコ内は,リーマンのゼータ関数のそのものです。
残った部分ですが,
と書き換えると分かりやすいです。クロネッカーの指標 は
であるから,
として, 関数のオイラー積で表すことができます。
結局,以下が成り立ちます。
デデキントのゼータ関数と 関数が結びつきました。これで随分と元々の類数公式に近づきましたね。
さて,あと一歩です。
式 に対して
の極限を考えます。単純に
とすると,発散してしまうので,適切に
をかけて極限をとる必要があります。
実際,以下の3つが成り立つことがわかります。
リーマンのゼータ関数の極限値はよいとして,問題は式 です。
デデキントのゼータ関数に対して における留数をとると,類数が出てくるのですね!非常に面白い!
オイラー積 の両辺に
をかけて,
の極限をとれば
が得られます。これはまさにディリクレの類数公式ですね!!
最後に,以上の議論を正当化するために,式 を証明しておきましょう。
 の証明:
の証明:
デデキントのゼータ関数の等式
に対して,ノルムが 以下のイデアルの個数
は
で表せる。
ここで,既に示した通り
が成り立ちます。
簡便のために, として
としておくと,
のとき
である。
さて,
であることに注意すると, のとき以下のように計算できる。
が成り立つ。
よって,
という不等式が得られる。あとは,右辺を に持っていくことができればよい。
このことを念頭にイプシロン・デルタ論法を用いて極限を計算する。
任意にあたえられた に対して,以下を満たすような十分大きな整数
をとる:
のとき
のとき
このように設定すれば,以下が成り立つ:
以上に 倍して
の極限をとると
となる。 は任意にとれるから,右辺はいくらでも
に近づけることができる。
したがって,
よって, より,
が得られた。
まとめ
今日はディリクレの類数公式とデデキントのゼータ関数の関連について解説しました。
類数公式については「代数」「幾何」「解析」のそれぞれの考察が入り混じっていて,非常に面白い証明でしたね。
証明を簡単に振り返ると:
- 代数パートでは,イデアル類群の構造(逆元)をうまくつかって「イデアルの密度」を「二次形式の格子点の密度」の議論に帰着させました。
- 幾何パートでは,「二次形式の格子点の密度」を「楕円の面積」に帰着させる方法を紹介しました。この際に,楕円の面積は判別式にのみ依存することもわかりました。
- 解析パートでは,「イデアルの密度」をデデキントのゼータ関数の解析的な性質を用いて計算する方法を紹介し,実際に類数と結びつくことを示しました。また,オイラー積の等式を利用して,二次体の場合は
関数によって計算できることも示しました。この計算も面白かったですね。
これまでも「デデキントのゼータ関数」という名前と定義くらいは知っていたのですが,単なる「ゼータ関数のそっくりさん」といった程度の理解でした。ところが「類数を計算する」というこんなに面白い応用があったのですね。解析のパートで紹介した「 の極には
の類数の情報が含まれている」という点は,今後じっくり味わってみたいと思います。デデキントのゼータ関数に興味を持っていただけたでしょうか。
それでは,今日はこの辺で。