「23」とフェルマーの最終定理 - tsujimotterのノートブック

本日は 2/23 ということで、この日付にまつわる楽しい数学の話をしたいと思います！

お話したいのは、23 という数そのものが持つ性質についてです。

f:id:tsujimotter:20210222234128p:plain:w400

$23$ は素数なので、素数についての話かと思った方もいるかもしれません。

もちろん、素数であることは大事なのですが、それだけではありません。 $23$ は次のような特徴を持つ素晴らしい数でもあるのです。

$p$ を3以上の素数としたとき、
$p$ 次円分体の類数が $1$ より大きくなる最小の $p$ は $23$ である

整数論を学んだ人にとっては、円分体や類数の意味が理解でき、そこから23の性質に感動を覚える人も少なくないかと思います。

一方で、円分体や類数をまったく知らない人にとっては、上の説明だけでは何のことかわかりませんよね。私自身、何度か一般向けの講演で上の事実を紹介したことがあるのですが、難しくて理解できなかったという方も多いのではないかと思います。

そんな方でも、今回こそは23の魅力について理解できるようになる、そんな解説を目指したいと思います。

円分体や類数といった概念は、実はフェルマーの最終定理という世紀の難問（現在は定理）と密接に結びついています。今日はこの関係について、できるだけわかりやすく解説することを目標にしたいと思います。

2/23という日に、今日の日付を、 $23$ という数を好きになってもらえたら嬉しいです！

目次：

1. フェルマーの最終定理の歴史

2. 円分体の整数との関係

3. クンマーの問題提起：素因数分解の一意性

4. クンマーのアイデア1：イデアルと類数

5. クンマーのアイデア2：正則素数pにおけるFLT(p)の解決

6. おわりに

参考文献

関連記事

1. フェルマーの最終定理の歴史

今から約380年くらい昔、ピエール・ド・フェルマーによって次の「予想」が提出されました。

フェルマーの最終定理

$n$ を $3$ 以上の任意の整数とする。このとき

$x^n + y^n = z^n \tag{1}$

を満たす $xyz \neq 0$ なる整数解 $(x, y, z)$ は存在しない。

この定理の主張について、フェルマー自身は論文としてはまとめていません。彼が携えていたディオファントスの著書「算術」という本の余白に、上記の主張が書き込まれているのが彼の死後発見されたのです。そこに添えられた以下のフレーズはあまりに有名ですね。

「この定理に関して、私は真に驚くべき証明を見つけたが、この余白はそれを書くには狭すぎる。」

実は、フェルマー本人は $n = 4$ の場合についての証明のアイデアを残しています。

「 $n = 4$ の場合」というのは、上の定理の主張において「 $n$ を $3$ 以上の任意の整数とする」の部分を「 $n = 4$ とする」のように置き換えたものを考えるということですね。

フェルマー本人としては、任意の $n$ に対しても同じ方法で証明できると思っていたようです。フェルマー自身が解いたと主張していること、また、この命題がフェルマーの残した未解決の最後の「定理」という理由により、今日「最終定理」と呼ばれているわけですね。

そこから360年ほどたって、任意の $n$ についてのフェルマーの最終定理が、アンドリュー・ワイルズ（1995年）によって証明されたという事実は、数学好きの皆さんはよくご存知かと思います。本当の意味で定理になったというわけですね。

解決に至る過程は、大変紆余曲折しています。これから紹介する内容は、ワイルズの証明とは直接的には関係しないものとなりました。しかしながら、以降で述べる内容はフェルマーの最終定理を語る上で大変重要な歴史であるとともに、今回紹介する $23$ のエピソードを理解する上で必要な話ですので、丁寧に振り返ってみたいと思います。

まず、上で述べたように、フェルマー自身が $n = 4$ のときのフェルマーの最終定理を解決しました。以後、「 $n = \; ?$ のときのフェルマーの最終定理」というのは煩雑なので、 $\newcommand{\flt}{\operatorname{FLT}} \flt(n)$ と表すことにしましょう。フェルマーは $\flt(4)$ を解決したというわけですね。

その後、以下のように個別の $n$ について解決されていきました。

$\flt(n)$	解決年	解決した数学者
$\flt(4)$	1630年代	フェルマー
$\flt(3)$	1770年	オイラー
$\flt(5)$	1820年	ディリクレ、ルジャンドル
$\flt(7)$	1839年	ラメ

この辺までが個別の $n$ についての研究です。ここまでで既に200年以上経っているわけですね。

$n$ が大きくなるにつれて、次第に証明が難しくなっていきます。個別の事例の解決がだんだんと複雑になっていくので、数学者たちはもっと一般な $n$ で証明できる方法はないかと考えるようになりました。

実は、フェルマーの最終定理は $\flt(4)$ と奇数の素数 $p$ についての $\flt(p)$ だけ解決すればよいことが分かります。つまり

$n = 3, 4, 5, 7, 11, 13, 17, 19, 23, \ldots$ （以下、素数が続く）

だけ考えれば十分というわけです。

もし $\flt(a)$ が成り立つと仮定すると、 $\flt(ab)$ が成り立つことが次の要領で証明できます。

背理法で示します。もし

$x^{ab} + y^{ab} = z^{ab}$

が存在すると仮定すると

$(x^{b})^a + (y^{b})^a = (z^{b})^a$

が成り立つことになります。これは $\flt(a)$ の解 $(x^b, y^b, z^b)$ が存在することを意味しますが、これは $\flt(a)$ が成立するという仮定に反しますね。

こんな要領で、 $n = 4$ と $n$ が素数の場合のみ証明すれば、 $n \geq 3$ であるすべての整数に対して $\flt(n)$ が成り立つことが証明できるわけです。

よって、 $n = 3, 4$ が既に証明されているので $5$ 以上のすべての素数 $p$ に対して $\flt(p)$ を示せばよいことになります。問題が素数に帰着されたということですね。

とはいえ、素数は無限に存在しますので、解決すべき問題が無限にあるのは変わりません。

ソフィー・ジェルマンという人が、「ソフィー・ジェルマン素数」という素数 $p$ に限って言えば、 $\flt(p)$ を解決したと発表しています。ただし、少し専門的になりますが「ファースト・ケースと呼ばれる条件に限って」という条件付きの解決です。

そんな中、 $\flt(7)$ を解決したラメという数学者が、こんなことを言い出します。任意の素数 $p$ で $\flt(p)$ が解決した、と。

2. 円分体の整数との関係

ラメが考えたのは、およそこんなことです。

一般の素数 $p$ で考えるのは大変なので、ひとまず $p = 3$ で説明しましょう。 $\flt(3)$ に整数解 $(x, y, z)$ が存在すると仮定します：

$x^3 + y^3 = z^3$

ここで「 $x, y, z$ のいずれも $p$ で割り切れない場合」のみを考えます。このような状況をファーストケースといって、「 $x, y, z$ のいずれかが $p$ で割り切れる場合」をセカンドケースということにします。一般にセカンドケースの方が圧倒的に証明が難しくなりますが、ここではファーストケースの場合のみを考えるということですね。

このとき、左辺 $x^3+y^3$ を整数の範囲を超えて次のように「因数分解」します：

$x^3 + y^3 = (x + y)(x + \zeta_3y)(x + \zeta_3^2y)$

$\zeta_3$ は $1$ の原始3乗根と呼ばれるものです。

$1$ の3乗根（3乗して $1$ になる数）は、複素数の範囲で $3$ つあります。 $1$ も $1$ の3乗根です（ $1^3 = 1$ なので）。1の原始3乗根とは「 $3$ 乗してはじめて $1$ となる数」のことで、 $1$ を除いた残り2つが $1$ の原始3乗根となります。

原始3乗根を複素数平面で考えると、単位円を3等分する位置関係にあります。

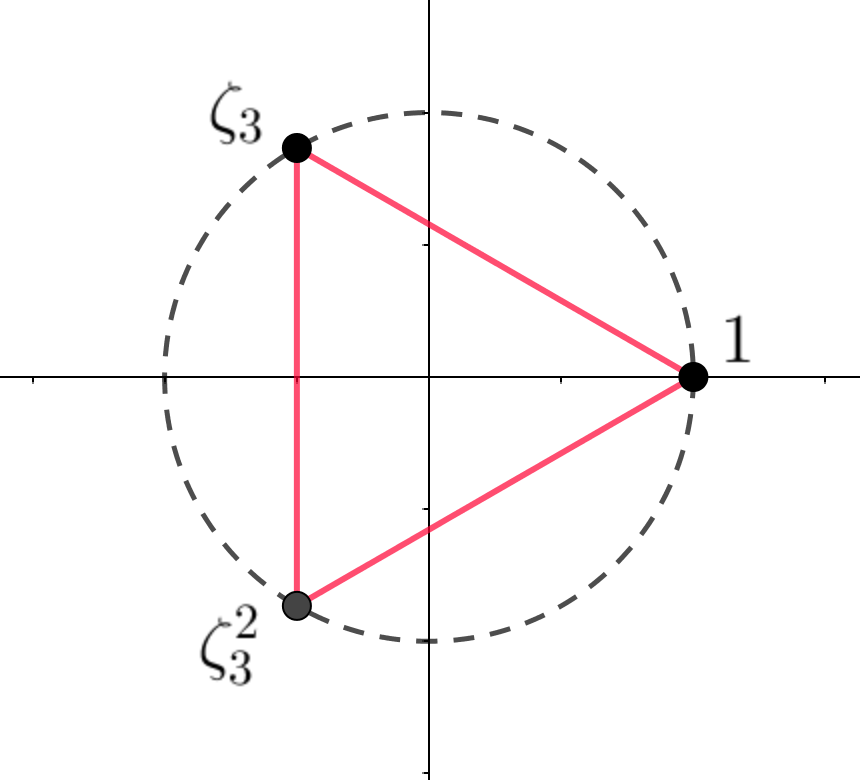
f:id:tsujimotter:20210222122526p:plain:w300

さて、上の因数分解が成り立つことを確認するために、まず1の原始3乗根 $\zeta_3$ における基本的な等式を2つ導きましょう。

$\zeta_3 \zeta_3^2 = 1$ （掛けて $1$ ）
$\zeta_3 + \zeta_3^2 = -1$ （足して $-1$ ）

まず、 $\zeta_3$ は3乗して $1$ になる数ですから、 $\zeta_3^3 = 1$ です。ここからただちに

$\zeta_3 \zeta_3^2 = 1$

であることがわかります。

また、同じく $\zeta_3^3 = 1$ より $\zeta_3^3 - 1 = 0$ であり、左辺を因数分解すると

$\zeta_3^3 - 1 = (\zeta_3 - 1)(\zeta_3^2 + \zeta_3 + 1)$

となります。これが $0$ に一致するわけですね。 $\zeta_3 \neq 1$ であったことを思い出すと

$\zeta_3^2 + \zeta_3 + 1 = 0$

であり

$\zeta_3^2 + \zeta_3 = -1$

であることが導かれます。

このようにして、2つの等式

$\zeta_3 \zeta_3^2 = 1$
$\zeta_3 + \zeta_3^2 = -1$

が導かれるわけですね。

以上の等式を使って、上の因数分解の式を導きたいと多います。右辺を展開して左辺に一致することを確認しましょう。

$\begin{align} (x + y)(x + \zeta_3y)(x + \zeta_3^2y) &= (x + y)(x^2 + (\zeta_3 + \zeta_3^2)xy + \zeta_3 \zeta_3^2 y^2) \\ &= (x + y)(x^2 - xy + y^2) \;\;\;\;\;\; (\because \text{2つの等式を使った}) \\ &= x^3 + y^3 \end{align}$

さて、 $\flt(3)$ の式を因数分解したことによって

$(x + y)(x + \zeta_3y)(x + \zeta_3^2y) = z^3$

という式が得られたわけですが、ここから何が言えるでしょうか。

まず、この左辺の式は、整数に加えて $\zeta_3$ や $\zeta_3^2$ が含まれた3つの数 $x+y, x+\zeta_3y, x+\zeta_3^2y$ の積となっています。これは私たちの知っている「整数」を拡張した概念になっています。

私たちが普段「整数」と読んでいるものは、有理数 $\frac{a}{b}$ の中で特に $b = 1$ （分母が $1$ ）である数のことです。これまで整数から有理数を作っていくという流れで考えていた方は、一回頭を切り替えて、整数とは「有理数の中で特に整数的な存在」というように発想をシフトさせましょう。

すると同じように「有理数に対応する概念」を考えて、その中で特に「整数的な存在」を議論することができます。

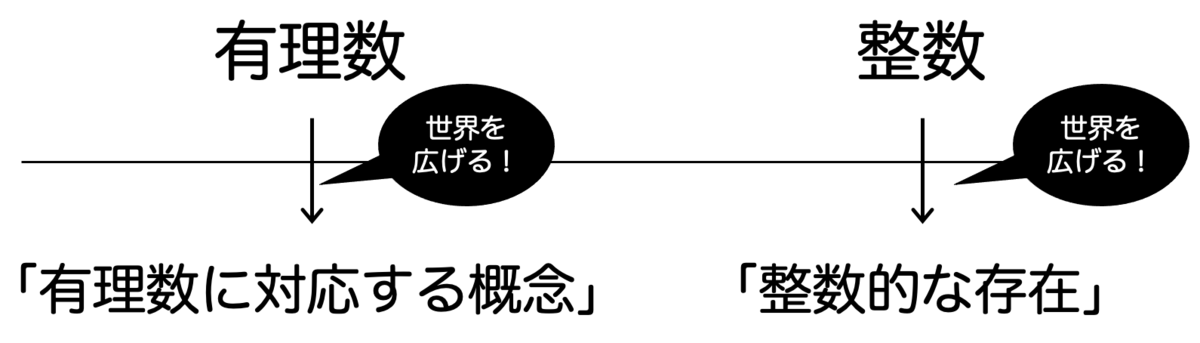
f:id:tsujimotter:20210222180748p:plain:w400

有理数に対応する概念として、ここでは「円分体」という概念を定義します。（冒頭の $23$ の性質の中で登場した用語ですね！）

「有理数」と「 $1$ の原始3乗根 $\zeta_3$ 」を含む四則演算ができる数の集まり（数学的には「有理数と $1$ の原始3乗根 $\zeta_3$ を含む最小の体」）を 3次円分体といいます。あるいは、次数を省略して単に円分体といいます。

3次円分体の中の「整数的な存在」のことを 3次円分体の整数といいます。具体的には、 $3$ 次円分体の中で特に

$\text{(整数)} + \text{(整数)}\,\zeta_{3}$

と表せる数が3次円分体の整数となります。

「おかしい、 $\zeta_3^2$ が入っていないぞ」と思った人は賢い人です。実は、先ほど計算した式から

$\zeta_3^2 = -1 - \zeta_3$

が言えるので、 $\zeta_3^2$ はすべて $1$ と $\zeta_3$ に置き換えることができるのです。

たとえば、 $x + \zeta_3^2 y$ の場合は

$\begin{align} x + \zeta_3^2 y &= x + (-1-\zeta_3)y \\ &= (x-y) + (-1)\zeta_3 y \end{align}$

のように表せます。 $(x-y)$ と $(-1)$ はどちらも整数なので、これは3次円分体の整数ですね。

改めて対応関係をまとめておきます：

f:id:tsujimotter:20210222181144p:plain:w400

円分体を導入することで、 $\flt(3)$ の式の因数分解は

$(x + y)(x + \zeta_3y)(x + \zeta_3^2y) = z^3$

という「3次円分体の整数における因数分解」であったと考えることができます。つまり、3次円分体の整数 $A, B, C$ を

$\begin{align} A &= x + y \\ B &= x + \zeta_3 y \\ C &= x + \zeta_3^2 y \end{align}$

とおいて

$ABC = z^3$

という、3次円分体の整数における等式と見ることができるわけですね。

ここから先に議論を進めるために、通常の整数論における「積を分解するテクニック」を活用することにします。上と同じような状況で、整数 $a, b, c, d$ が

$abc = d^3$

だったとしましょう。ここで、 $a, b, c, d$ は通常の意味での整数とします。

ここでもし $a, b, c$ がどの2数の組も互いに素（ $a$ と $b$ 、 $b$ と $c$ 、 $c$ と $a$ のそれぞれが公約数を持たない）であれば、 $a, b, c$ が3乗数であることを示すことができます。

たとえば、 $d = 2\cdot 3 \cdot 5$ だったとして

$abc = (2\cdot 3 \cdot 5)^3$

としましょう。このとき、 $a, b, c$ がそれぞれ互いに素であれば

$a = 2^3$ 、 $b = 3^3$ 、 $c = 5^3$

であったり、あるいは

$a = 1^3$ 、 $b = 6^3$ 、 $c = 5^3$

のようになるでしょう。いずれの場合も、3乗数になっていることに注意してください。

もし3乗数でなかった場合、 $a, b, c$ に共通の約数が入ってしまいます。これは、 $a, b, c$ が互いに素であるという仮定に反しますので、そのような状況にはならないということですね。

これと同じようなことが、3次円分体の整数においても実行できます。つまり

$ABC = z^3$

が成り立つとき、 $A, B, C$ が（3次円分体の整数において）どの2数の組も互いに素であれば、 $A, B, C$ はいずれも「だいたい」3乗数になります。「だいたい」というのは、3乗数に加えて「単数」が付くということです。「単数」というのは、通常の整数の中で $\pm 1$ のような存在で、逆数をとってもまた3次円分体の整数になる特別な数です。このように余計な部分がついてしまうのですね。

なお「どの2数の組も互いに素である」という仮定についてですが、フェルマーの最終定理のファーストケースであれば成り立つことを示せます。だから、この仮定は重要なのですが、とにかくファーストケースであればこの部分の議論をうまく進められます。

このことから、ある3次円分体の整数 $U, V, W$ と「単数」と呼ばれる数 $e_1, e_2, e_3$ を用いて

$A = e_1 U^3$

$B = e_2 V^3$

$C = e_3 W^3$

と表すことができます。あとは3次円分体の整数 $A, B, C, U, V, W$ および単数 $e_1, e_2, e_3$ であって、上の３つの式を満たすものが存在しないことが言えれば $\flt(3)$ が解決します。

実際、 $\flt(3)$ のオイラーの証明は、だいたいこんなやり方で実行されています。

より一般に、3以上の素数 $p$ について $\flt(p)$ を証明しようとすると、 $1$ の原始 $p$ 乗根 $\zeta_p$ を用いて、 $p$ 次円分体の整数を考えることになります。

そこで、先ほどと同じ議論によって、 $p$ 次円分体の整数で因数分解します。

$(x+y)(x+\zeta_p y)\cdots(x+\zeta_{p}^{p-1}) = z^p$

左辺の各因数を $A_1, A_2, \cdots, A_p$ としたとき、ファーストケースであれば、

$A_i = \text{(単数)} \cdot \text{(}p\text{乗数)}$

のようにかけるというわけですね。

これをもとに、そんな解は存在しないことが証明できるはずだ。よって、 $\flt(p)$ は解決した、と。そう、ラメは考えました。

また、まったく同時期にコーシーという数学者も、同じような発想で $\flt(p)$ を解決したと名乗り出ました。そして、二人はフェルマーの最終定理の解決の先取権を争って論争を引き起こします。自分の方が先にこれを解決したのだと。

そんなことをしているうちに、ある男が上記の証明に疑問を投げかけます。

「この証明 $p = 23$ でうまくいきませんよ。」

男の名は、エルンスト・クンマーといいます。

3. クンマーの問題提起：素因数分解の一意性

クンマーが指摘した「ラメの勘違い」は大きく３つあります。

そもそもラメはファーストケースしか考えていない
単数についての考察が十分でない
$p$ 次円分体の整数では、一般には素因数分解の一意性が成り立たない

最後の指摘がイメージしづらく、かつ、今回の話の主題となるので、この点についてのみ説明します。

問題の箇所は

$A_1 A_2 \cdots A_p = z^p$

から、 $A_1, A_2, \ldots, A_p$ が互いに公約数を持たないという条件下で

$A_i = \text{(単数)}\cdot \text{(}p\text{乗数)}$

を導いた箇所です。

そもそもこの議論が、素因数分解の一意性に立脚した議論であるというのがポイントです。

ここが今回一番ややこしい箇所なので、もし難しいなと思ったら飛ばして進んでもらって大丈夫です。

$2$ 乗ぐらいに限定して同じことをやってみます。

$A_1 A_2 = z^2$

このとき、 $A_1$ と $A_2$ が互いに素であるとき、 $A_1$ と $A_2$ はともに $2$ 乗数であることを示しましょう。

右辺を $z = p_1 p_2$ のように一意的に素因数分解するというのが、最初のステップです。簡単のために $z$ が2素数の積だとします。すると

$A_1 A_2 = p_1^2 p_2^2$

ですね。ここで左辺の $A_1, A_2$ は互いに素なので、 $A_1$ と $A_2$ には相異なる素数が入るはずです。すると、 $p_1$ に着目したときに、 $p_1^2$ は $A_1$ に入るか $A_2$ に入るかのいずれかになります。 $A_1$ と $A_2$ のそれぞれに $p_1$ が1個ずつ入るということはありえません。

同じように、 $p_2$ に対して着目すると、 $p_2^2$ が $A_1$ の約数に入るか、 $A_2$ の約数に入るかのいずれかになります。よって、 $A_1$ も $A_2$ も素因数は偶数個ずつ入るので2乗数になるというわけですね。

以上の議論は、 $z$ の素因数分解に基づいているのですが、同時に「素因数分解の一意性」も使っていることに注意する必要があります。

素因数分解が一意でないとは、 $z$ を2通りの素因数分解によって

$z = p_1 p_2 = q_1 q_2$

と表したときに、 $\{p_1, p_2\}$ と $\{q_1, q_2\}$ が異なることを言います。

もしそんな状況が発生したと仮定しましょう。このとき、 $z^2$ における一方の $z$ を $p_1 p_2$ 、もう一方の $z$ を $q_1 q_2$ と表すことができます。これを代入すると　

$A_1 A_2 = (p_1 p_2)(q_1 q_2)$

となります。ここで右辺の素因数 $p_1, p_2, q_1, q_2$ のすべてが異なるので、どんな風に組み合わせても $A_1$ と $A_2$ が互いに素となります。たとえば

$A_1 = p_1 q_1, \;\; A_2 = p_2 q_2$

のように分けたとしても、 $A_1$ と $A_2$ が互いに素なのでよいでしょう。このようにしてしまうと、 $A_1$ と $A_2$ はもはや2乗数ではなくなってしまいます。これまでの論法が完全に崩れてしまいます！！

クンマーはこのようなことを指摘したわけですね。ラメもこれには素因数分解の一意性が一般には成り立たないことには気づかなかったのでしょう。

実際、通常の意味の整数の世界では素因数分解の一意性は成り立ちます。これは想像ですが、まさか世界を広げたらそれが成り立たなくなるなんて思わなかった、ということでしょうか。

不幸なことに、最初の方の素数 $p = 3, 5, 7, 11, \ldots, 19$ では素因数分解の一意性は成り立ってしまいます。そのため、一般には素因数分解の一意性が成り立たないということに、なかなか気づけないわけですね。

最初に素因数分解の一意性が成り立たなくなるのが $p = 23$ というわけです。やっと $23$ が出てきました。

$23$ 次円分体の整数においては、素因数分解の一意性は成り立ちません。このことを端的に示すのはなかなか難しいです。

たとえば、 $23$ 次円分体の整数では、 $6$ の素因数分解が2通りになります：

$\begin{matrix} 6 &=& 2\times 3 \\ &=& (\zeta_{23} +\zeta_{23}^4+\zeta_{23}^9+\zeta_{23}^{16}+\zeta_{23}^2+\zeta_{23}^{13}+\zeta_{23}^{3}+\zeta_{23}^{18}+\zeta_{23}^{12}+\zeta_{23}^{8}+\zeta_{23}^{6}) \\ && \;\;\;\; \times (\zeta_{23}^{22} +\zeta_{23}^{19}+\zeta_{23}^{14}+\zeta_{23}^{7}+\zeta_{23}^{21}+\zeta_{23}^{10}+\zeta_{23}^{20}+\zeta_{23}^{5}+\zeta_{23}^{11}+\zeta_{23}^{15}+\zeta_{23}^{17}) \end{matrix}$

なかなかすごいことになっていますね。 $23$ 次円分体の整数で、素因数分解が2通りになる例はあまり本には乗っていないのですが、上の例はtsujimotterがコンピュータを使って見つけたものです。

$p_1 = 2$
$p_2 = 3$
$q_1 = \zeta_{23} +\zeta_{23}^4+\zeta_{23}^9+\zeta_{23}^{16}+\zeta_{23}^2+\zeta_{23}^{13}+\zeta_{23}^{3}+\zeta_{23}^{18}+\zeta_{23}^{12}+\zeta_{23}^{8}+\zeta_{23}^{6}$
$q_2 = \zeta_{23}^{22} +\zeta_{23}^{19}+\zeta_{23}^{14}+\zeta_{23}^{7}+\zeta_{23}^{21}+\zeta_{23}^{10}+\zeta_{23}^{20}+\zeta_{23}^{5}+\zeta_{23}^{11}+\zeta_{23}^{15}+\zeta_{23}^{17}$

とすると

$6 = p_1 p_2 = q_1 q_2$

と分解され、素因数分解が2通りになっています。
（正確には「 $p_1, p_2$ と $q_1, q_2$ が互いに同伴でないこと」もいう必要がありますが、それも確認しています。）

そんなわけで、 $p = 23$ のように素因数分解の一意性が成り立たないような世界においては、同じような方針ではフェルマーの最終定理を解決することはできません。これがクンマーの問題提起だったわけですね。

これを聞いた人は「23は残念な数であるな・・・これさえいなければ、フェルマーの最終定理が成り立つかもしれないのに」と思うかもしれません。

ところが、問題提起をしたクンマー自身は、そんな $p = 23$ でも適用できる解決策を持ち合わせていたのです。

4. クンマーのアイデア1：イデアルと類数

クンマーは「イデアル」という道具を発明し、それを使って「大部分の $p$ において」フェルマーの最終定理を解決しました。

正確にいうと、クンマーは「理想数」というものを考えました。これが後世の数学者であるデデキントによって整理され、現在では「イデアル」と呼ばれています。理想数はイデアルそのものではありませんが、今回は現代的な視点からイデアルを使って説明します。

先ほど、 $p = 23$ の円分体の整数においては、素因数分解の一意性が成り立たないのが問題だったわけです。

$6 = p_1 p_2 = q_1 q_2$

ここで、クンマーは発想を変えたわけですね。

数の世界で素因数分解の一意性が成り立たないのであれば、一意性が成り立つような「理想的な数」の世界を考えよう、というのです。

一体何を言っているんだと思うかもしれません。

クンマーはこう考えました。

もし、上の素因数分解において $p_1, p_2, q_1, q_2$ がさらに分解されて

$p_1 = A B$
$p_2 = C D$
$q_1 = A C$
$q_2 = B D$

となるとしましょう。このとき、 $6$ の素因数分解は

$6 = ABCD$

と表すことができます。これで分解が一意的になりました。そんな都合のよい $A, B, C, D$ を考えようと思うわけですね。

ひとつ言っておくと、このような $A, B, C, D$ は、（円分体のときのように）単に新しい数を加えるだけではうまく実現しません。

ここではあくまで新しい数を追加するのではなく、同じ $p$ 次円分体の整数の中だけで、数を集めることによって数に相当する概念を構成するのです。これがイデアルです。

イデアルを具体的に構成する方法についてはここでは紹介できませんが、こちらの記事で解説しています。興味を持った方はご覧になってください。
tsujimotter.hatenablog.com
tsujimotter.hatenablog.com

クンマーがやったことの説明を急ぎましょう。

つまり、クンマーは数の世界から、イデアルの世界に話を広げて考えたわけですね。

円分体の整数をイデアルの世界に埋め込んだときに、イデアルの世界の方が「数」の種類が多いのです。そのため、送った数はイデアルの世界で一意的に分解されるというわけです。

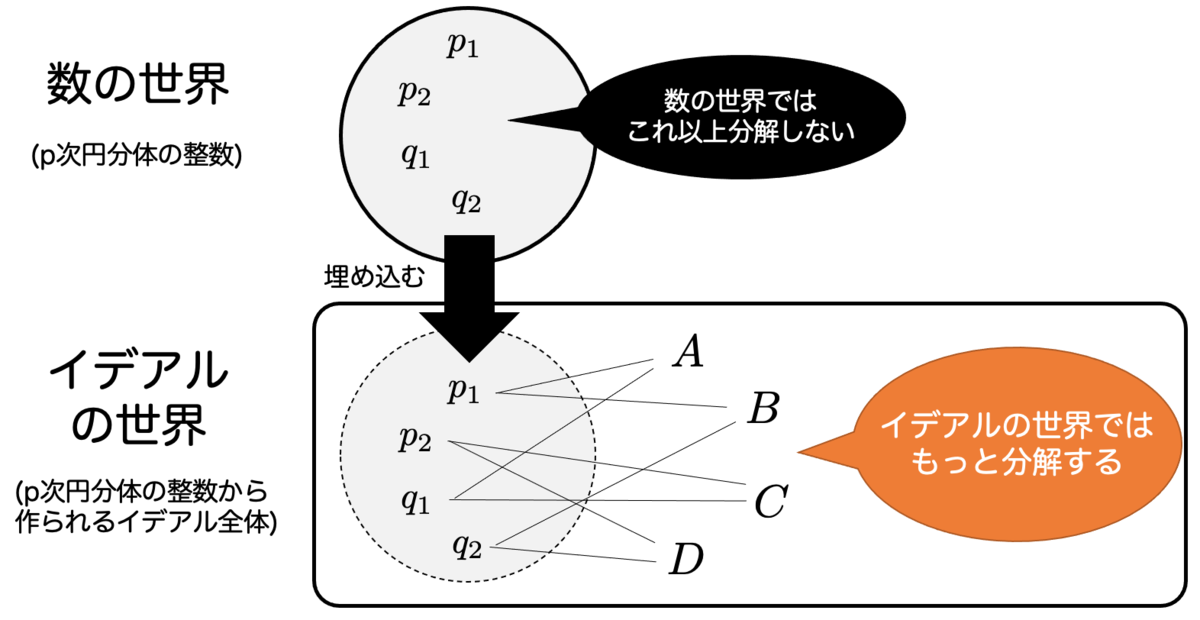
f:id:tsujimotter:20210223120337p:plain:w420

このようにしてあげると、イデアルの世界に送り込んだ

$A_1 A_2 \cdots A_p = z^p$

という等式から

$A_i = \text{(あるイデアル)}^p$

という等式を導くことができます。これはまだイデアルの世界の等式です。

フェルマーの最終定理は数の世界の問題なので、ここから数の世界に引き戻されければならない。

しかし、一般にイデアルの世界が数の世界より大きいので、引き戻せるかどうかはイデアルによるわけです。具体的には、上の「あるイデアル」がちゃんと数の世界に戻って来ればよい。該当のイデアルにちょうど対応する数が存在するかどうかが焦点になります。

f:id:tsujimotter:20210222235313p:plain:w420

ここでクンマーはイデアルの世界の大きさを定量的に測る方法に着目しました。

数の世界をイデアルの世界に埋め込んだとき、イデアルの世界はちょうどその何倍の大きさにあるかを考えたのです。

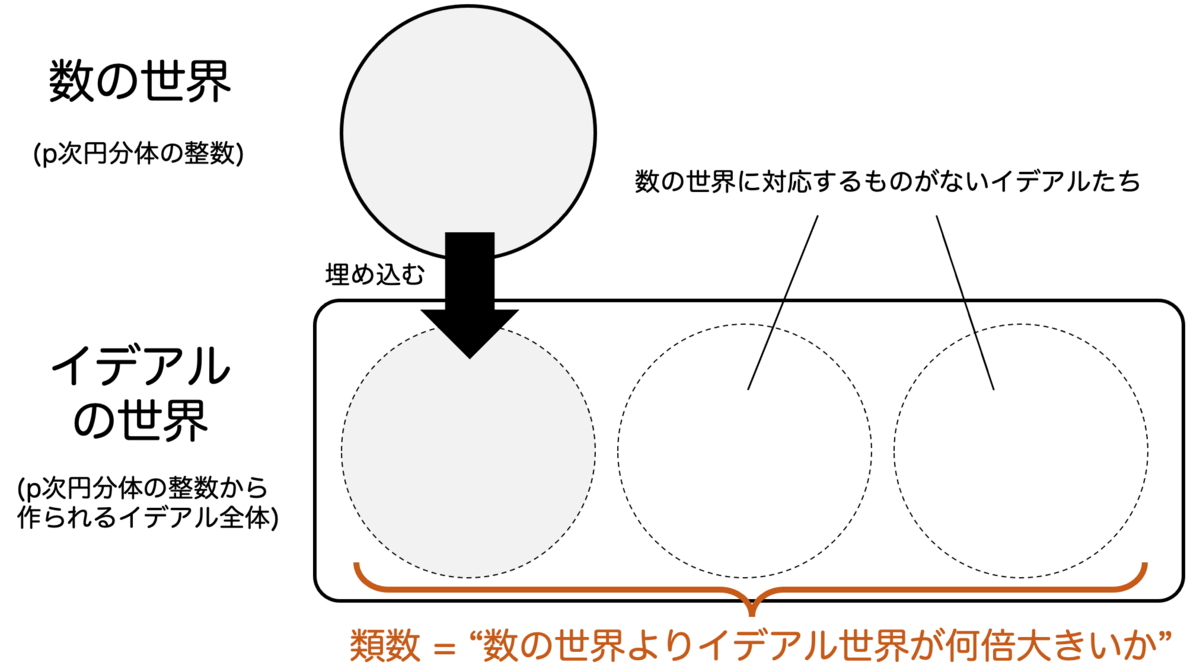
f:id:tsujimotter:20210222182403p:plain:w420

この「数の世界の何倍大きいか」という量を類数といいます。数の世界とイデアルの世界がちょうど同じ大きさであれば類数1、イデアルの世界が $2$ 倍大きければ類数2、のような感じです。

$p = 3$ における円分体は、数の世界はちょうどぴったりイデアルの世界に一致することが知られています。よって類数1。だから、数の世界であっても素因数分解の一意性が成り立ってしまっていたのですね。たまたま。

同じく、 $p = 5$ における $5$ 次円分体も類数1、 $7$ 次円分体、 $11$ 次円分体も類数1、・・・のように続いていきます。

そして、初めて類数が1より大きくなるのが $23$ 次円分体というわけですね。この数の世界では、イデアルが数の世界のちょうど $3$ 倍の大きさになります。つまり類数3 ということです！

f:id:tsujimotter:20210222182625p:plain:w420

類数が $1$ より大きいので、素因数分解の一意性が成り立ちません。だから、ラメの方法ではうまくいかないというわけですね。

5. クンマーのアイデア2：正則素数pにおけるFLT(p)の解決

クンマーは証明できない理由を分析しただけではありません。なんと、これを使って、類数が1より大きい場合でも証明できる方法を発明してしまったのです。

3以上の素数 $p$ に対して $p$ 次円分体の類数を計算します。この類数が $p$ 自身で割り切れないとき、この $p$ を正則素数ということにします。類数が $p$ で割り切れるとき、非正則素数ということにします。

クンマーは、すべての正則素数 $p$ における $\flt(p)$ のファーストケースを一挙に解決してしまったのです。

すごいことですね！！

アイデアは、類数を使ってイデアルを数の世界に戻すということです。ざっくり述べると、イデアルの世界の等式

$A_i = \text{(あるイデアル)}^p\$

において、「あるイデアル」の部分が、数の世界に戻ってくることを示せばよいわけですね。これは、類数が $p$ で割り切れないという仮定と、ユークリッドの互除法を使って示すことができます。

この証明の部分は非常に面白いのですが、技巧的なのでやめておきましょう。詳しく知りたい方は、以下の記事にまとめましたので読んでみてください：
tsujimotter.hatenablog.com

一方、セカンドケースにおいては、ファーストケースのようにはなかなくうまくいきません。具体的には単数の取り扱いに問題があり、その部分に証明上の大きな困難があります。

しかしながら、なんと $p$ が正則素数のとき、クンマーの補題という道具を使えば、セカンドケースにおいても証明できてしまったのです。なんということでしょう。

そんなわけで、 $p$ が正則素数のときには $\flt(p)$ は完全に解決してしまったといって良いですね。あまりにすごい結果だったので、当時フェルマーの最終定理に掛けられていたパリ学士院の賞金が、クンマーに贈られてしまったそうです。まだ非正則素数では解決していないのにです。

こうなってくると、正則素数とはいったいどんな数なのか、ということが気になってきますよね。各 $p$ について、 $p$ 次円分体の類数が知りたくなってくるかと思います。

実際、見てみるとこうなります。

素数 $p$	$p$ 次円分体の類数
$3$	$1$
$5$	$1$
$7$	$1$
$11$	$1$
$13$	$1$
$17$	$1$
$19$	$1$
$23$	$3$ （初めて1より大きい！）
$29$	$8$
$31$	$9$
$37$	$37$ （非正則素数！）

$p = 3$ から $p = 19$ までは類数 $1$ であり、 $p = 23$ で初めて類数 $3$ になります。なんか嬉しくなりますね！

そして、 $p = 23, 29, 31$ は類数が $1$ より大きくなるわけですが、どれも $p$ では割り切れないので正則素数になります。

したがって、 $p = 31$ までは正則素数なので、クンマーの方法を使って $\flt(p)$ が証明できてしまうわけですね！

その次にくるのが $p = 37$ です。 $37$ 次円分体の類数は、なんと $37$ です。つまり、類数を $p$ が割り切るので、非正則素数ということになるわけです。

類数という数は興味深いですね。だんだんと愛着が湧いてきたのではないでしょうか。

類数が $1$ 以上だと、素因数分解の一意性が成り立たないので、ちょっと困る数であるという認識を一旦は持ったかもしれません。

しかしながら、クンマーによって、類数が1より大きい場合でも正則素数に限ればうまくいくという方法が見出されました。クンマーの方法でも非正則素数についてはうまくいかないわけですが、実は非正則素数はそれ自体非常に奥深い構造を内包していることが知られています。

フェルマーの最終定理を探求するにあたって、 $p = 23$ で一旦は困難が訪れますが、困難が人類を成長させたのですね。23はその困難の最初のステップであったというわけです。

クンマー以後、円分体をはじめとした「拡張された数の世界」を考えて、そのイデアルや類数などを研究する学問は「代数的整数論」と呼ばれて発展してきました。

フェルマーの最終定理では、最終的には直接的な形で用いられることはありませんでした。しかしながら、たとえば「カタラン予想」など、代数的整数論は数多くの難問を解決する足がかりとなりました。

また、大きな世界で素数がどのように素イデアル分解されるのかを調べた「類体論」や、特定の拡大を考えたときに類数がどのように増えていくのかを調べた「岩澤理論」など、非常に魅力的な理論を生み出したのも代数的整数論です。

その意味でクンマーの創始した理論は、現代数学に計り知れない影響を与えるものとなっています。

6. おわりに

最後に、今日の話をまとめたいと思います。覚えていただきたいのは「23」という数の次の特徴です：

$p$ を3以上の素数としたとき、
$p$ 次円分体の類数が $1$ より大きくなる最小の $p$ は $23$ である

最初に意味不明だった呪文のような主張も、ここまで読んでいただけ方には理解いただけるのではないかと思います。

素数 $p$ についてのフェルマーの最終定理において、1の原始 $p$ 乗根を加えた世界「円分体」で考えることが重要なのでした。そのとき、素因数分解の一意性が成り立たないという事態が発生します。それは類数が $1$ より大きいということを意味します。

そして、類数が1より大きくなる最初の例こそが $p = 23$ だったというわけなのですね。しかしながら、この困難こそが代数的整数論の創始に繋がったというわけです。

今日2/23にみなさんにお伝えしたいのは、23は代数的整数論の歴史のまさに始まりであったということです。23という数の存在が、私たちにその世界の奥深さを教えてくれたのだと思うと、私は感動を覚えずにはいられません。

ぜひ、23を見た時には、このような代数的整数論の深い世界を思い浮かべていただきたいと思います。そして、ぜひ数の性質に興味を持っていただけたら幸いです。

整数論の世界を楽しんでいただけたでしょうか？

それでは、今日はこの辺で！
（よろしければ感想などお待ちしております！）

参考文献

フェルマーの最終定理について書かれたブルーバックスの本です。私がフェルマーの最終定理を勉強し始めたとき、最初に熟読したのがこの本だったかと思います。非常にわかりやすく、面白く書かれているのでぜひご覧になってください。
私の今回の記事も、この本の影響を受けている部分は多いにあるかと思います。

なお、今回の記事執筆にあたって、主に歴史の部分について参考にさせていただきました。

フェルマーの大定理が解けた！　オイラーからワイルズの証明まで (ブルーバックス)

作者:足立恒雄
発売日: 2013/11/08
メディア: Kindle版

tsujimotterのノートブックでは、他にも関連する話題を書いています。今回の話に興味を持ってより詳しく知りたいと思った方は、お時間のあるときにぜひご覧になってください。順番に読む必要はありませんので、気になったものからどうぞ。
tsujimotter.hatenablog.com
tsujimotter.hatenablog.com
tsujimotter.hatenablog.com
tsujimotter.hatenablog.com
tsujimotter.hatenablog.com