（独自研究）素数生成多項式と虚2次体の類数

今回の記事は、素数がたくさん登場する多項式

$f(X) = X^2 + X+ 41$

に関連する話題です。今回は私がこの式について考えているうちに、思いついて実施してみた独自研究について紹介したいと思います。どこかの本に書いてある話ではないので、誤りを含んでいる可能性も大いにあるかと思います。また、十分な調査ができているわけではないので、独自性もはっきりとしていません。その点をご了承の上で読んでください。

今回の記事は発展的な内容になっています。オイラーの素数生成多項式について、より基本的な事項を知りたい方は、まずはこちらの記事を読むのをお勧めします：
tsujimotter.hatenablog.com

今回は論文を意識したフォーマットで書いているため、普段のブログ記事より内容が難しく、堅めの書き振りになっている点をご了承ください。また、虚2次体に関する基本的な知識を前提とします。

追記：2020.01.21
やはりといいますか、当然と言いますか、先行研究として類似のアイデアの研究はありました。勉強も兼ねてブログにまとめていますので、次の記事もぜひご参照ください：
tsujimotter.hatenablog.com

追記：2020.01.22
Proposition 1.の証明におきまして、 $p = 2$ の場合を適切に考慮し忘れていたため、その点を修正しました。Proposition 2. の証明に影響はありません。

1. Introduction

1772年、EulerはBernoulliに宛てた手紙の中で、素数を生成する2次多項式について述べている。すなわち、素数 $q$ に対し、

$f_{q}(X) = X^2 + X + q \tag{1}$

と定義すると、素数 $q = 2, 3, 5, 11, 17, 41$ に対し $f_q(X)$ に整数 $X = 0, \ldots, q-2$ を代入した値がすべて素数になることを発見した。これをオイラーの素数生成多項式という。

Rabinovitch (1913)は $f_q(X)$ が素数生成多項式である条件と、対応する虚2次体の類数が1である条件の間の同値性を示した。すなわち、 $q$ を任意の素数であるとき、 $f_{q}(X)$ が $X = 0, \ldots, q-2$ においてすべて素数になるための必要十分条件は、虚2次体 $\mathbb{Q}(\sqrt{1-4q})$ の類数が1であることである。

さらに、Baker (1966)やStark (1967)により、類数が1である虚2次体が独立に決定されており、その系として上記の条件を満たす $q$ は $q = 2, 3, 5, 11, 17, 41$ のときに限られる。

ここで、任意の素数 $q$ に対し、2次多項式 $f_{q}$ を考えて

$\displaystyle P_1(q) = \frac{\# \{ X \in \mathbb{Z} \mid 0 \leq X\leq q-2 \;\; \text{s.t.}\;\; f_{q}(X)\colon \text{prime} \} }{q-1} \tag{2}$

とする。 $P_1(q)$ を素数生成確率と呼ぶことにする。名前の通り、 $0\leq X\leq q-2$ に対して $f_{q}(X)$ が素数になる割合を表す。

また、虚2次体 $K$ に対しその判別式を $d_K$ としたとき、対応する類数を $h_{d_K}$ と表すことにする。このとき、Rabinovitchの定理は次のように言い換えられる。

Theorem 1 (Rabinovitch, 1913)

$q$ を任意の素数とすると、次が成り立つ：

$P_1(q) = 1 \; \Longleftrightarrow \; h_{1-4q} = 1 \tag{3}$

上記の定理は類数1と $P_1(q) = 1$ が同値という主張であるが、類数が2以上については $P_1(q) < 1$ が成り立つ以上のことは言及されていない。先行研究においても、このような観点に基づく研究はないように思える。

そこで本研究では、計算機により虚2次体 $\mathbb{Q}(1-4q)$ の類数 $h_{1-4q}$ を計算し、特に類数 $2$ 以上のケースにおける $P_1(q)$ の振る舞いを観察する。 $P_1(q)$ が類数 $h_{1-4q}$ に反比例するというヒューリスティックな仮定に基づいて分析したところ、少なくとも $q < 100000$ においては $f_q$ は予想より素数になりやすいという「バイアス」が存在することを発見した。

2. Prime generationg polynomials

素数生成多項式と類数の関係について、関連する研究について述べたい。

[1] によれば、Hardy and Littlewoodは1923年の論文で、2次形式が表現する素数の分布について、次の発見的な公式を予想として与えている。

Conjecture (Hardy and Littlewood, 1923)

$a > 0, b, c$ を $\text{gcd}(a, b, c) = 1, \; b^2 - 4ac$ は平方数ではなく， $a+b, c$ は双方とも偶数ではない整数とする*1．このとき， $am^2 + bm + c$ の形の素数が無限に多く存在し， $x$ より小さな $am^2 + bm + c$ の形の素数の個数 $\pi_{aX^2 + bX + c}(x)$ は漸近的に

$\displaystyle \pi_{aX^2 + bX + c}(x) \sim \frac{\varepsilon C}{\sqrt{a}} \frac{\sqrt{x}}{\log(x)} \prod_{p > 2,\; p \mid \text{gcd}(a, b)} \frac{p}{p-1}$

によって与えられる．ここで

$\displaystyle \varepsilon = \begin{cases} 1 & (a+b\colon \text{odd}), \\ 2 & (a+b\colon \text{even}), \end{cases}$

$\displaystyle C =\prod_{p>2, \; p\not| a} \left(1 - \frac{\left(\frac{b^2 - 4ac}{p}\right)}{p-1}\right) \;\; \left(\frac{\ast}{p}\right)\colon \text{Legendre symbol}$

とする．

この予想を、正の整数 $A$ に対し $f_A(X)$ なる特別な場合に適用したものが、次の予想である：

$f_A(X) = X^2 + X + A$ の $A$ を $1 - 4A$ は平方数ではない整数とする．このとき

$\displaystyle \pi_{f_A(X)}(x) \sim C(A) \frac{2\sqrt{x}}{\log(x)}$

によって与えられる．ここで

$\displaystyle C(A) =\prod_{p>2} \left(1 - \frac{\left(\frac{1 - 4A}{p}\right)}{p-1}\right)$

とする．

Shanksは1975年に $C(41) = 3.3197732$ なることを決定し、FungとWilliamsは1990年にさまざまな $A$ に対して、 $C(A)$ と $f_A(10^6)$ を具体的に計算している。今まで計算された $C(A)$ の値の中で最大のものは、2003年にJacobsonとWilliamsが発表した70桁のある整数 $A$ に対する $C(A) = 5.5338891$ である。

以上の結果は、一般の $X > 0$ なる整数 $X$ についての、 $f_A(X)$ における素数の分布についてである。一方で、 $X$ の範囲を $X = 0, \ldots, p-2$ に限定させたとき、その素数分布がどのようになっているか明らかではない。本研究ではこのような問題を扱いたい。

なお、素数生成多項式としては、Frobenius (1912)とHendy (1974)によってEulerの $f_q(X) = X^2 + X + q$ と異なるものが3つ得られている [1]。 $p, q$ を素数として

$\begin{align} g_{1, q}(X) &= 2X^2 + q \tag{4} \\ g_{2, q}(X) &= 2X^2 + 2X + \frac{q+1}{2}, \; \; q\equiv 1 \pmod{4} \tag{5} \\ g_{3, p, q}(X) &= pX^2 + pX + \frac{p+q}{4}, \;\; p < q, \; pq \equiv 3 \pmod{4} \tag{6} \end{align}$

とする。

また、

$\displaystyle P_2(q) = \frac{\# \{ X \in \mathbb{Z} \mid 0 \leq X\leq q-1 \; \text{s.t.}\; g_{1, q}(X)\colon \text{prime} \}}{q} \tag{7}$

$\displaystyle P_3(q) = \frac{\# \{ X \in \mathbb{Z} \mid 0 \leq X\leq \frac{q-3}{2} \; \text{s.t.}\; g_{2, q}(X)\colon \text{prime} \}}{\frac{q-1}{2}} \tag{8}$

$\displaystyle P_4(p, q) = \frac{\# \{ X \in \mathbb{Z} \mid 0 \leq X\leq \lfloor \frac{p+q}{8}-4 \rfloor \; \text{s.t.}\; g_{3, p, q}(X)\colon \text{prime} \}}{\lfloor \frac{p+q}{8}\rfloor -3} \tag{9}$

を定義する。このとき、次が得られる：

Theorem 2 (Frobenius (1912), Hendy (1974))

$q$ を任意の素数とすると、次が成り立つ：

$P_2(q) = 1 \; \Longleftrightarrow \; h_{-8q} = 2 \tag{10}$

ここで、 $-8q$ は虚2次体 $\mathbb{Q}(\sqrt{-2q})$ の判別式である。

同様に、以下のような事実が示されている。
・ $q$ を $q \equiv 1\pmod{4}$ なる任意の素数とすると、次が成り立つ（Frobenius (1912), Hendy (1974)）：

$P_3(q) = 1 \; \Longleftrightarrow \; h_{-4q} = 2 \tag{11}$

・ $p < q$ を $pq \equiv 3\pmod{4}$ なる任意の素数とすると、次が成り立つ（Frobenius (1912), Hendy (1974)）：

$P_4(p, q) = 1 \; \Longleftrightarrow \; h_{-pq} = 2 \tag{12}$

3. Experimental

代表的な素数生成多項式である $f_q(X) = X^2 + X + q$ と $g_{1, q}(X) = 2X^2 + q$ において、対応する虚2次体の類数 $h_{1-4q}, h_{-8q}$ と素数生成確率 $P_1(q), P_2(q)$ について観察したい。

まず、実験前の簡単な分析として、素数生成多項式の値が素数であることと、その素数を分解した素イデアルの関係について、2つの命題を述べたい。これらの命題の証明は記事末尾で述べる。

Proposition 1.

$q$ と $n$ を整数とする． $f_q(X) = X^2 + X + q$ とし， $d = 1-4q$ は平方因子を持たないとする．

このとき， $p$ が $f_q(n)$ を割り切る素数ならば $p$ は $\mathbb{Z}[\frac{1+\sqrt{d}}{2}]$ で惰性しない．

Proposition 2.

$q$ を素数， $n = 0, 1, \ldots, q-2$ を整数とする． $f_q(X) = X^2 + X + q$ とし， $d = 1-4q$ は平方因子を持たないとする．また， $p$ を $f_q(n)$ を割り切る最小の素数とし， $P$ を $p$ を割り切る $\mathbb{Z}[\frac{1+\sqrt{d}}{2}]$ の素イデアルとする．

このとき，次が成立：

$f_q(n)$ は素数 $\;\;\Longleftrightarrow \;\;$ $P$ は単項イデアル

Proposition 1より、 $f_q(n)$ の素因数 $p$ は

$(p) = PP'$

と素イデアル分解される。 $P'$ は $P$ の共役である。

このときProposition 2は、 $f_q(n)$ が素数であることと、 $P$ が単項イデアルであることが同値であることを主張している。したがって、 $0 \leq n \leq q-2$ に対して $f_q(n)$ が素数になる確率 $P_1(q)$ は、対応する素イデアル $P$ が単項イデアル類に属する確率と一致することになる。すなわち、素数生成確率は $P$ の単項イデアルになりやすさを表しているといえる。

ここで、ヒューリスティックな仮定：「 $P$ がイデアル類群 $C_{\mathbb{Q}(\sqrt{1-4q})}$ の各類に入るのは同様に確からしい」を置く。すなわち

$\displaystyle P_1(q) \approx \frac{1}{h_{1-4q}} \tag{13}$

であると考えたい。

$P$ がどのイデアル類に入りやすいかということについて、特段の性質は知られていないため、このような仮定は一定程度妥当であると予想される。以下では、実際にそのようなヒューリスティックな仮定がどの程度妥当なのかを、実際に虚2次体の類数および素数生成確率を計算することで検証したい。

4. Results & Discussion

$q < 100000$ なる素数 $q$ に対して、 $1-4q$ が平方因子を持たない場合について、虚2次体 $\mathbb{Q}(\sqrt{1-4q})$ の類数 $h_{1-4q}$ と対応する $P_1(q)$ を計算する。その結果を散布図にまとめたものがFig. 1である。横軸は $h_{1-4q}$ 、縦軸は $P_1(q)$ であり、青色の点が実際の実験結果、オレンジ色の点が $1/h_{1-4q}$ を表している：

f:id:tsujimotter:20210119192542p:plain:w600

Fig 1. Relation between prime density of $f_q$ and $h_{1-4q}$

$q < 100000$ のケースにおいては、図からみて分かるように、 $1/h_{1-4q}$ を $P_1(q)$ が大きく上回る傾向があるということがわかる。すなわち、 $f_q(X)$ の最小の素因数 $p$ を分解して得られる素イデアル $P$ は、当初予想していた以上に単項イデアルに入りやすい傾向があるということである。

実際、 $P_1(q) < \frac{1}{h_{1-4q}}$ となったのは、 $q < 100000$ においては $q = 13, 23, 29, 31, 103$ のケースのみであって、残りはすべて $P_1(q) \geq \frac{1}{h_{1-4q}}$ となっている。

また、同様に $2 < q < 50000$ なる素数 $q$ に対して、虚2次体 $\mathbb{Q}(\sqrt{-2q})$ の類数 $h_{-8q}$ と対応する $P_2(q)$ を計算する。その結果を散布図にまとめたものがFig. 2である（横軸は $h_{-8q}$ 、縦軸は $P_2(q)$ ）：

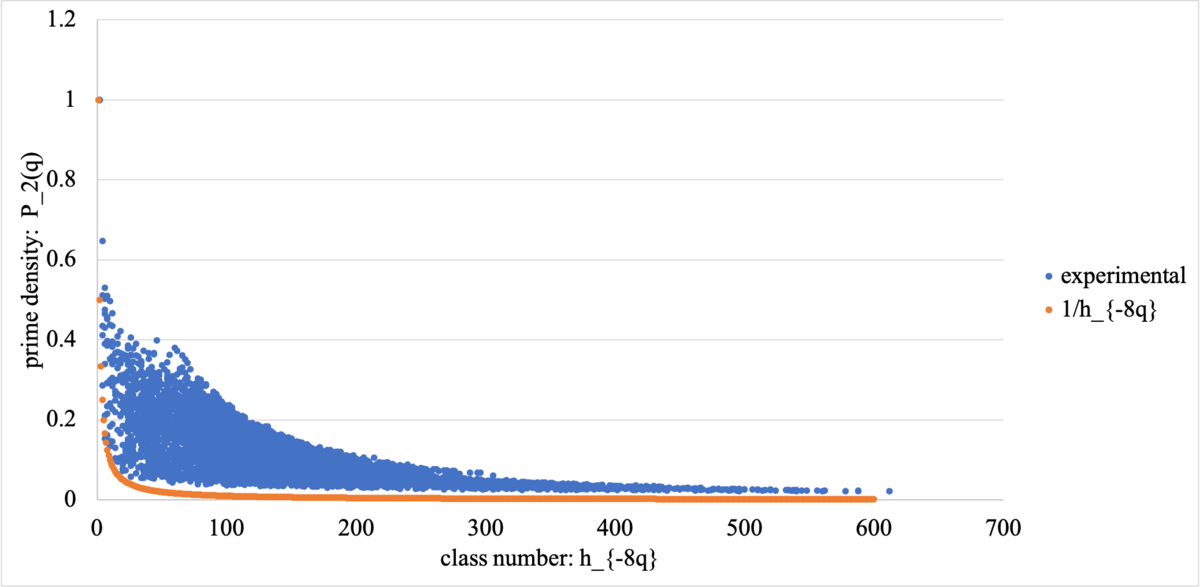
f:id:tsujimotter:20210119192603p:plain:w600

Fig 2. Relation between prime density of $g_{1,q}$ and $h_{-8q}$

Fig 2.のケースにおいても、同様の傾向が見られる。すなわち、 $P_2(q) < \frac{1}{h_{-8q}}$ となったのは、 $q < 50000$ においては $q = 13$ のケースのみであることがわかった。残りはすべて $P_2(q) \geq \frac{1}{h_{-8q}}$ である。

今回の結果およびProposition 2を合わせて考えると、 $0 \leq X \leq q-2$ の範囲で $f_q(X)$ を割る最小の素因数 $p$ は、虚2次体 $\mathbb{Q}(\sqrt{1-4q})$ で分解されたときに単項イデアルになりやすいということである。これは各イデアル類に入る確率が同様に確からしいという予想に反しており、非自明な事実であると考えられる。

ここで議論が必要なのは、単項イデアルは特別入りやすいのか否かという点である。実際、分解された素イデアル $P$ の分布が偏っており、多く入る類とそうでない類が存在し、結果として相対的に単項イデアルに入る確率が上がっているという可能性も考えられる。

これについても、実際、分解された素イデアル $P$ がどの類に入るのかを調べる実験を行った。 $q < 300$ における結果を次に示す：

-7, [1]
-11, [2]
-19, [4]
-43, [10]
-51, [4, 8]
-67, [16]
-91, [10, 12]
-115, [13, 15]
-123, [14, 16]
-163, [40]
-187, [26, 20]
-211, [19, 33/2, 33/2]
-235, [34, 24]
-267, [36, 30]
-283, [28, 21, 21]
-291, [18, 27/2, 27, 27/2]
-331, [34, 24, 24]
-355, [27, 19, 23, 19]
-403, [68, 32]
-411, [16, 17, 15/2, 37, 15/2, 17]
-427, [71, 35]
-435, [30, 42, 14, 22]
-451, [23, 29/2, 49/2, 11, 49/2, 29/2]
-523, [37, 20, 53/2, 53/2, 20]
-547, [67, 69/2, 69/2]
-555, [44, 53, 15, 26]
-595, [54, 40, 25, 29]
-627, [54, 21, 21, 60]
-651, [26, 8, 47/2, 15/2, 10, 56, 47/2, 15/2]
-667, [65, 71/2, 30, 71/2]
-691, [50, 41, 20, 20, 41]
-715, [70, 29, 30, 49]
-723, [68, 23, 66, 23]
-763, [79, 71/2, 40, 71/2]
-771, [43, 61/2, 21/2, 67, 21/2, 61/2]
-787, [60, 57/2, 79/2, 79/2, 57/2]
-795, [70, 75, 19, 34]
-843, [52, 15, 51/2, 77, 51/2, 15]
-907, [132, 47, 47]
-915, [38, 80, 43/2, 25/2, 8, 34, 43/2, 25/2]
-955, [100, 81/2, 57, 81/2]
-1003, [111, 95/2, 44, 95/2]
-1027, [114, 109/2, 33, 109/2]
-1051, [84, 51/2, 127/2, 127/2, 51/2]
-1123, [105, 34, 107/2, 107/2, 34]
-1131, [49, 16, 85/2, 23/2, 11, 98, 85/2, 23/2]
-1171, [67, 68, 41/2, 24, 24, 41/2, 68]

1列目が $d = 1-4q$ を表し、2列目で $0\leq q \leq q-2$ の $q-1$ 個の $f_q(X)$ に対し、その最小の素因数 $p$ を割り切る素イデアル $P$ が、 $h_{1-4q}$ 個のイデアル類に属する回数を表している。 $h_{1-4q}$ 個のうち一番左のデータが単項イデアル類に入った回数である。

1つの $p$ に対し、素イデアルは $(p) = PP'$ と分解されるが、 $P, P'$ が同じイデアル類に入る場合と、異なるイデアル類に入る場合がある。後者の場合、 $P$ を選ぶか $P'$ を選ぶかはまったく任意であるため、恣意的な偏りを作ることができてしまう。そこで、上の結果では、 $P, P'$ が入った類に対して、それぞれ $+1/2$ を加算するようにしている。この場合、 $P, P'$ が同じイデアル類に属する場合は、 $+1$ となる。

結果を見ると、最初の10数個はほとんど偏りがないように見えるが、それ以降の $q$ については分布は確かに偏っているように見える。しかしながら、これはあくまで主観的な判断であり、この偏りを説明するための分析手法が必要である。

5. Conclusion

本研究では、オイラーの素数生成多項式 $f_q(X) = X^2 + X + q$ が $0 \leq X < q-2$ の範囲で素数を生成する確率について、虚2次体 $\mathbb{Q}(\sqrt{1-4q})$ の類数 $h_{1-4q}$ に関連づけて分析を行った。

ヒューリスティックな議論により、素数生成確率 $P_1(q)$ はおよそ類数 $h_{1-4q}$ の逆数に一致すると予想されたが、実際の $P_1(q)$ は $1/h_{1-4q}$ より高い傾向にあることがわかった。特に、　 $q < 100000$ の範囲においては、 $P_1(q) < 1/h_{1-4q}$ となるのは $q = 13, 23, 29, 31, 103$ の場合のみであった。このような $f_q(X)$ が素数を生成しやすいという「バイアス」は従来の研究では知られていないと思われる。

$f_q(X)$ のみならず、 $g_1(X) = 2X^2 + q$ においても同様の傾向は見られており、同様の素数生成多項式についてもこのようなバイアスの存在は示唆される。

本研究においては、このようなバイアスが存在するためのメカニズムを明らかにするには至らなかったが、今後の課題としたい。発見された例外ケース（ $P_1(q) < 1/h_{1-4q}$ なる $q$ ）は小さいものに限られていたため、有限個の $q$ を除いて $P_1(q) \geq 1/h_{1-4q}$ が言えるどうかについても気になるところである。また、 $p \mid f_q(X)$ を割り切る素イデアル $P$ が属するイデアル類に偏りがあるかどうかも今後調査が必要である。今回の評価は例外ケースを除いて下からの評価を与えているように思えるが、上からの評価を与えることはできるかどうかも考えたい。

References

[1] P. Ribenboim著, 吾郷孝視訳編, "素数の世界その探索と発見（第2版）", 共立出版株式会社 (2001).

上記には載せていませんが "partial prime dense" というキーワードの研究があるそうで、本研究に関連しそうですが、著者の調査不足によりまだ把握できておりません。

Acknowledgements

nishimura（@icqk3）さんには、Proposition 2'.の $\Longleftarrow$ （Proposition 2. の $\Longrightarrow$ の対偶）証明のアイデアをいただきました。また、2020年5月30日開催のロマンティック数学ナイト@オンラインにおいて、聴講者の方（@simizut22 さん）から質問をいただき、この質問が本研究の着想のきっかけとなりました。

素数と2次体の整数論の勉強会（#ゆるにじたい）メンバーの皆様にも感謝申し上げます。皆様との議論のおかげで、特にProposition 1, 2の証明について、論理立てて整理することができました。

Appendix: Proof of Proposition 1 & 2

前述したProposition 1およびProposition 2について証明する。命題を次の通り再掲する：

Proposition 1.

$q$ と $n$ を整数とする． $f_q(X) = X^2 + X + q$ とし， $d = 1-4q$ は平方因子を持たないとする．

このとき， $p$ が $f_q(n)$ を割り切る素数ならば $p$ は $\mathbb{Z}[\frac{1+\sqrt{d}}{2}]$ で惰性しない．

(Proof)
$d = 1 - 4q \equiv 1 \pmod{4}$ かつ $d$ は平方因子を持たないことより、 $\mathbb{Z}\left[\frac{1+\sqrt{d}}{2}\right]$ は $\mathbb{Q}(\sqrt{d})$ の整数環である。よって、虚2次体 $\mathbb{Q}(\sqrt{1-4q})$ における、有理素数 $p$ の素イデアル分解法則を考える。

$p = 2$ である場合と $p \neq 2$ である場合に分けて考える。

$p = 2$ の場合：
$f_q(n) = n^2 + n + q = n(n+1) + q \equiv q \pmod{2}$ であるため、 $2 \mid f_q(n)$ であるならば $q$ は偶数である。このとき、 $\mathbb{Q}(\sqrt{1-4q})$ の判別式は $d = 1-4q \equiv 1 \pmod{8}$ である。素イデアル分解法則より、 $2$ は $\mathbb{Z}[\frac{1+\sqrt{d}}{2}]$ で分解する（惰性しない）。

$p \neq 2$ の場合：
仮定より、 $f_q(n) = n^2 + n + p \equiv 0 \pmod{p}$ である。両辺を $4$ 倍して

$4n^2 + 4n + 1 - (1 - 4q) \equiv 0 \pmod{p}$

であるが、移項して

$(2n + 1)^2 \equiv 1 - 4q = d \pmod{p}$

である。ゆえに、 $p \mid d$ または $\left(\frac{d}{p}\right)$ である。

したがって素イデアル分解法則より、 $p$ は $\mathbb{Z}\left[\frac{1+\sqrt{d}}{2}\right]$ で惰性しない。

(End of proof)

また、Proposition 2については、対偶をとった次の命題を示すことにする。

Proposition 2'.

このとき，次が成立：

$f_q(n)$ は合成数 $\;\;\Longleftrightarrow \;\;$ $P$ は非単項イデアル

(Proof)

$(\Longrightarrow)$ の証明：

仮定より、 $f_q(n)$ は合成数であるから $f_q(n) > 1$ より $2$ 以上の整数 $L$ を用いて

$f_q(n) = pL$

と表せる。 $p$ の最小性 $p \leq L$ と $f_q$ の単調性および $n < q-1$ より

$p^2 \leq pL \leq f_q(n) < f_q(q-1) = q^2$

である。すなわち、 $p < q$ が成立する。

一方、 $\mathbb{Z}[\frac{1+\sqrt{d}}{2}]$ において $(p)$ を割り切る素イデアルを $P$ とすると、Proposition 1. より $P$ の共役 $P'$ を用いて $(p) = PP'$ と表せる。もし、 $P$ が単項イデアルだと仮定すると

$P = (\alpha), \;\;\; \alpha = x+y\frac{1+\sqrt{d}}{2}$

なる有理整数 $x, y \in \mathbb{Z}$ が存在する。

もし、 $y = 0$ だとすると、 $(p) = (x)^2 = (x^2)$ となり $p$ が素数であることに反するので不合理。ゆえに $y\neq 0$ である。

このとき

$(p) = PP' = (N(P)) = (N(\alpha))$

であるから、 $p > 0, \; N(\alpha) > 0$ より $p = N(\alpha)$ である。すなわち

$p = N(\alpha) = (x + y\frac{1+\sqrt{d}}{2})(x + y\frac{1-\sqrt{d}}{2}) = x^2 + xy + \frac{1-d}{4}y^2$

が成立する。

これを $4$ 倍して $p < q$ および $q = \frac{1-d}{4}$ を用いると

$4x^2 + 4xy + (1-d)y^2 = 4p < 4q = 1-d$

が得られる。移項して

$\begin{align} 1 &> 4x^2 + 4xy + (1-d)y^2 + d \\ &= (2x+y)^2 + (y^2 - 1)|d| \end{align}$

となるが、 $y\neq 0$ より右辺は $0$ 以上の整数となる。ゆえに

$\begin{cases} 2x + y = 0 \\ y^2 - 1 = 0 \end{cases}$

が成立する。これを満たす $(x, y) \neq (0, 0)$ は存在しない。

したがって、 $P$ が単項イデアルという仮定が誤りであった。

$(\Longleftarrow)$ の証明：

Proposition 1. より $P$ は惰性しない素イデアルだから、 $P$ は原始的イデアル。よって、 $\omega = \frac{1+\sqrt{d}}{2}$ とすると、 $P$ は標準基底を用いて

$P = [a, b+\omega]$

と表せる。ここで、 $a > 0$ であり、整数 $b$ は $b = 0, \ldots, a-1$ の範囲で一意的。

$(p) = PP' = (N(P))$ より $p = N(P)$ であり、一方で標準基底の置き方より $N(P) = a$ でもある。したがって、 $a = p$ である。

また、 $P$ がイデアルであるための必要十分条件は

$a \mid N(b + \omega) = f_q(b)$

であるから、 $a = p < q$ と $b$ の一意性より $b = n$ である。

したがって、 $P = [p, n+\omega]$ と表せることがわかった。また、 $P = (p, n+\omega)$ でもある。

一方で、単項イデアル $Q = (n+\omega)$ は明らかに $Q \subset P$ であるが、 $P$ は単項イデアルではないという仮定より $Q \subsetneq P$ である。

また、 $Q \subset P$ より $N(P) \mid N(Q)$ であるが、特に $Q \subsetneq P$ より $N(P)$ は $N(Q)$ の非自明な約数である。 $N(Q) = N(n + \omega) = f_q(n)$ より、 $f_q(n)$ は合成数であることが示された。

(End of proof)

*1: $a+b$ が偶数になってはいけないなら、 $\varepsilon$ の定義がおかしいのでは？ 2020.01.21追記：これについては、「 $a+b, c$ は双方とも偶数ではない整数とする」を「「 $a+b, c$ は双方とも偶数」ではない整数とする」とすれば問題なさそうだというご指摘をいただきました。つまり、少なくともどちらか一方は奇数である、という仮定です。確かにこれであれば $\varepsilon$ の定義とも整合的です。