眠気と闘うあなたへ：素イデアル分解のすすめ

突然ですが、眠くて眠くてしょうがないときってありますよね。

スマホを開くことができれば、いろいろと目をさますコンテンツにアクセスすることができます。しかしながら、スマホを開くことができないときもありますよね*1。

ここには紙とペンしかない。眠気には耐えなければならない。

そんなときには「素イデアル分解」してみるのはいかがでしょう。

少しだけ前提知識の説明

素数 $p$ を適当に選びます。

これらの素数は、有理数体 $\mathbb{Q}$ 上では有理素数、つまり「分解できない数」というわけですが、 $\mathbb{Q}$ の拡大体 $K$ まで持ち上げると分解してしまうことがあります。

たとえば、 $K = \mathbb{Q}(\sqrt{-1})$ まで持ち上げると、 $p = 13$ の生成するイデアルは

$(13) = (2 - 3\sqrt{-1})(2 + 3\sqrt{-1}) \tag{1}$

のように素イデアル分解されてしまいますね。 $4n+1$ 型の素数は、 $K = \mathbb{Q}(\sqrt{-1})$ で２つの素イデアルに完全分解します。

一般に、代数体 $K$ を考えたときに、有理素数 $p$ の生成するイデアルは

$(p) = \mathfrak{P}_1^{e_1} \cdots \mathfrak{P}_g^{e_g} \tag{2}$

と一意に素イデアル分解されます。ただし、 $\mathfrak{P}_1, \cdots, \mathfrak{P}_g$ は重複を含まない $K$ の素イデアルとしておきます。

ここで、類体論を知っている人は、 $K/\mathbb{Q}$ がアーベル拡大であれば、与えられた $p$ が分解するかどうかは「 $an+b$ 型の素数は $K$ で完全分解する（惰性する・分岐する）」のように法則化されることを知っています。一方で、この法則だけでは、具体的にどのような素イデアルに分解されるかわかりません。

どうやって、計算すればよいのでしょう。

遊び方

ここでは、 $\mathbb{Q}$ に $\alpha$ を添加した代数体 $K = \mathbb{Q}(\alpha)$ を考えて、有理素数 $p$ の $K$ における素イデアル分解を求めたいと思います。

使うのは $\alpha$ の（ $\mathbb{Q}$ 上の）最小多項式 $f(X)$ です。最小多項式とは、 $f(\alpha) = 0$ を満たす $\mathbb{Q}$ 上既約な多項式のことですね。

$f(X)$ は既約なのでこれ以上分解できませんが、 $\bmod{p}$ で考えると、さらに分解できることがあります。

ここで、 $f(X)$ が $\bmod{p}$ で

$f(X) \equiv \varphi_1(X)^{e_1} \cdots \varphi_g(X)^{e_g} \pmod{p} \tag{3}$

と分解できるとしましょう。ここで、 $\varphi_1(X), \cdots, \varphi_g(X)$ は $\bmod{p}$ で（つまり $\mathbb{F}_p$ で）既約とします。

この $\bmod{p}$ で分解された多項式 $\varphi_1(X), \cdots, \varphi_g(X)$ に $\alpha$ を無理やり代入してみましょう。すると、 $K$ の数の組 $\varphi_1(\alpha), \cdots, \varphi_g(\alpha)$ ができます。実は、これを使って $p$ が素イデアル分解できるのです。

こんな風に。

$(p) = (p, \varphi_1(\alpha))^{e_1} \cdots (p, \varphi_g(\alpha))^{e_g} \tag{4}$

これ、すごくないですか！？

ちゃんとそれぞれのイデアル $(p, \varphi_1(\alpha)), \cdots , (p, \varphi_g(\alpha))$ は $K$ の素イデアルになっているのです。

「 $p$ の素イデアル分解」を求めるために、一見直接関係なさそうな「 $f(X)$ の $\bmod{p}$ における分解」を計算しているのが面白いと感じました。

実際、この計算は比較的簡単にできるのです。やってみましょう。

さぁ、計算してみよう

最初の $K = \mathbb{Q}(\sqrt{-1})$ における例を計算してみましょう。

$\alpha = \sqrt{-1}$ の最小多項式は $f(X) = X^2 + 1$ ですね。実際 $f(\alpha) = \alpha^2 + 1 = 0$ を満たします。

ここで、 $p = 13$ として、 $p$ の素イデアル分解を考えましょう。

上の方法によると、まず $f(X) = X^2 + 1$ を $\bmod{p}$ で分解してみる必要があります。

考え方はいろいろあると思うのですが、たとえば $X^2 - Y^2 = (X - Y)(X + Y)$ の形に持っていくとよいかもしれません。

$\bmod{13}$ では、

$\begin{align} X^2 + 1 &\equiv X^2 - 25 \\ &\equiv (X - 5)(X + 5) \pmod{13} \end{align}$

が成り立ちます。私は $13$ をたくさん引いて、定数項が平方数になるパターンを探す方法で考えました*2。

よって、

$f(X) \equiv (X - 5)(X + 5) \pmod{13} \tag{5}$

と分解できることがわかりました。この右辺の $(X - 5), (X + 5)$ が， $\varphi_1(X), \varphi_2(X)$ に相当します。

これらに $\alpha = \sqrt{-1}$ を代入して、 $\sqrt{-1} - 5, \sqrt{-1} + 5$ を得た上で

$(13) = (13, 5 - \sqrt{-1})(13, 5 + \sqrt{-1}) \tag{6}$

としたものが、 $p = 13$ の素イデアル分解です*3。

これで完成です！

f:id:tsujimotter:20171223233353p:plain:w360

実際、式 $(6)$ の右辺を計算すると

$\begin{align} &(13, 5 - \sqrt{-1})(13, 5 + \sqrt{-1}) \\ &= (13^2, 13(5 + \sqrt{-1}), 13(5 - \sqrt{-1}), (5 - \sqrt{-1})(5 + \sqrt{-1}) ) \\ &= (13^2, 13(5 + \sqrt{-1}), 13(5 - \sqrt{-1}), 26 ) \\ &= (13)(13, 5 + \sqrt{-1}, 5 - \sqrt{-1}, 2 ) \\ &= (13) \end{align}$

となり、たしかに左辺に一致していますね。また、素数は２次体において最大２つのイデアルにしか分解されないため、これらがただちに素イデアルとわかります。

こんな風に、素イデアル分解を求めることができるのです。

ちなみに、上は完全分解の例ですが、 $p = 11$ のように惰性する（つまり、 $K$ で分解しない）場合を考えてみましょう。

この場合は、 $\bmod{11}$ で $f(X)$ は分解しません。つまり、 $\bmod{11}$ で $f(X)$ は既約なのです。ということは、 $f(X)$ に $\alpha$ を代入しても $f(\alpha) = 0$ ですから、結局

$\begin{align} (11) &= (11, f(\alpha) ) \\ &= (11, 0 ) \\ &= (11) \end{align}$

となって、たしかに法則は成り立っていますね。あまり面白くないですが。

別の例でも

ほかの例でもやってみましょう。

$K = \mathbb{Q}(\sqrt{-5})$ として、 $p = 23$ の $K$ における素イデアル分解を計算してみましょう。

$\alpha = \sqrt{-5}$ の最小多項式 $f(X) = X^2 + 5$ を $\bmod{23}$ における分解を考えます。 $X^2 + 5$ に $23$ を足したり引いたりして、 $X^2 - Y^2$ の形に持って行きます。実際、 $69$ を引くと

$\begin{align} X^2 + 5 &\equiv X^2 - 64 \\ &\equiv (X - 8)(X + 8) \pmod{23} \end{align} \tag{7}$

が得られます。

少しだけ頭を使わないと見つけられないので、完全に単純作業になるわけではありません。なので、ちょうどいい具合に眠くなりません。

あとは、式 $(7)$ 右辺の $(X - 8), (X + 8)$ に $X = \alpha$ を代入して

$(23) = (23, 8 - \sqrt{-5})(23, 8 + \sqrt{-5}) \tag{8}$

として、 $p = 23$ の素イデアル分解が得られました。

やったね！

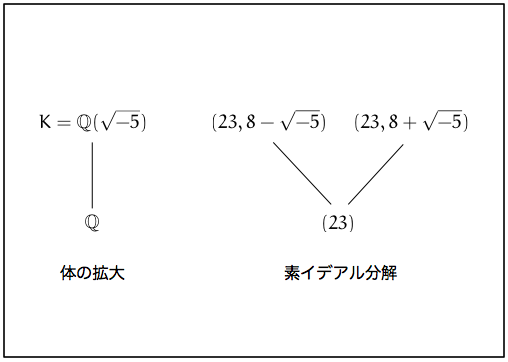
f:id:tsujimotter:20171223233424p:plain:w360

ちなみに、 $p = 23$ は $20n + 3$ 型の素数ですが、一般に $K = \mathbb{Q}(\sqrt{-5})$ においては、 $p = 20n+1, 20n+3, 20n+7, 20n+9$ 型の素数は完全分解します。

こんな感じで、本当に紙とペンさえあれば計算できます。ぜひ、みなさんも試してみてください！

今日はとても眠かったのですが、この素イデアル分解に助けられました。

少しだけ注意

ところで、 $K = \mathbb{Q}(\sqrt{-1})$ の例を思い出してください。

今回の方法では $p = 13$ に対して

$(13) = (13, 5 - \sqrt{-1})(13, 5 + \sqrt{-1}) \tag{6}$

という結果が得られました。一方で、冒頭で挙げた例では

$(13) = (2 - 3\sqrt{-1})(2 + 3\sqrt{-1}) \tag{1}$

となっていました。察しのよい人は気付いているかもしれませんが、これらの素イデアル分解は、少なくとも見た目上は異なって見えます。式 $(1)$ の右辺は単項イデアルの積になっていますが、式 $(6)$ の右辺はどちらも単項イデアルではありません。

実は、どちらも同じ素イデアル分解を与えているのですが、ぱっと見は同じであることはわかりませんね。

今回の方法は、 $\mathfrak{P} = (p, \varphi(\alpha) )$ の形で素イデアルの分解を与えるため、得られた素イデアルは単項イデアルとはなりません。この点には注意が必要です。

背景にある定理

代数的整数論の教科書をめくってみると、だいたいどの本にも、素イデアル分解を具体的に与える Kummer による定理*4が載っています。

定理（Kummer）

$K = \mathbb{Q}(\alpha)$ を代数体とし， $\alpha$ は代数的整数， $\alpha$ の $\mathbb{Q}$ 上の最小多項式を $f(X)$ とする（代数的整数なので最小多項式の係数は整係数）．また， $K$ の整数環が $\mathbb{Z}[\alpha]$ に一致すると仮定する．

$f(X)$ が $\bmod{p}$ で既約な多項式 $\varphi_1(X), \cdots, \varphi_g(X)$ の積に分解されるとする．

$f(X) \equiv \varphi_1(X)^{e_1} \cdots \varphi_g(X)^{e_g} \pmod{p}$

このとき， $p$ の生成するイデアルの素イデアル分解が以下のように与えられる：

$(p) = (p, \varphi_1(\alpha))^{e_1} \cdots (p, \varphi_g(\alpha))^{e_g}$

定理の意味するところは、遊び方のところで解説したので、ここでは細かい注意だけ述べておきます。

上の定理は、小野先生の「数論序説」の定理 2.17 を元に書き直したものです。下線部の仮定があるように、先の方法は任意の代数体に適用できるわけではなく、整数環に条件がついているようです。この条件だと、たとえば円分体 $\mathbb{Q}(\zeta_m)$ や $d \equiv 2, 3 \pmod{4}$ （ $d$ は平方因子を持たない）のときの二次体 $\mathbb{Q}(\sqrt{d})$ であればオーケーです。 $d \equiv 1 \pmod{4}$ のときの二次体 $\mathbb{Q}(\sqrt{d})$ も $\mathbb{Q}(\sqrt{d}) = \mathbb{Q}(\frac{1+\sqrt{d}}{2})$ と生成元を取り直せば $\mathcal{O}_K = \mathbb{Z}[\frac{1+\sqrt{d}}{2}]$ とできて定理が適用できます。

ちなみに、石田先生の「代数的整数論」の定理 13.1 でも、ほぼ同様の定理が述べられていますが、こちらはもう少し条件がゆるくなっています。 $K$ の整数環 $\mathcal{O}_K$ が $\mathbb{Z}[\alpha]$ に一致していなくても良いが「 $p$ が $(\mathcal{O}_K \colon \mathbb{Z}[\alpha])$ を割り切らない」という条件が必要なようです（詳しくは参考文献を参照）。

用法用量を守って正しくお使いください。

それでは今日はこの辺で。

補足

$\mathfrak{P} = (p, \varphi(\alpha))$ が素イデアルになることは割と簡単に証明できそうなので、以下に書いてみます。

まず $K$ が代数体より、（0 でない）素イデアルは極大イデアルになります。したがって

$\mathfrak{P}$ が（0 でない）素イデアル　 $\Longleftrightarrow$ 　 $\mathcal{O}_K/\mathfrak{P}$ が体

が成り立ちます。 $\mathcal{O}_K = \mathbb{Z}[\alpha]$ の仮定より

$\mathbb{Z}[\alpha] / \mathfrak{P}$ が体であれば $\mathfrak{P}$ は素イデアル

が成り立ちます。よって、 $\mathbb{Z}[\alpha] / \mathfrak{P}$ が体であることを確認しましょう。

$\mathfrak{P} = (p, \varphi(\alpha))$ として

$\begin{align} \mathbb{Z}[\alpha] / \mathfrak{P} &= \mathbb{Z}[\alpha] / (p, \varphi(\alpha) ) \\ &\simeq \mathbb{Z}[X] / (p, f(X), \varphi(X) ) \\ &\simeq \mathbb{F}_p[X] / (f(X), \varphi(X) ) \end{align}$