マチンの公式と14個のペル方程式 - tsujimotterのノートブック

今回の記事は「シリーズ：連分数とペル方程式」の３日目（最終日）の記事となっています。関連する記事はこちらからご覧いただけます。

今日のテーマは、円周率のマチンの公式です：

$\displaystyle 4\arctan\frac{1}{5} - \arctan\frac{1}{239} = \frac{\pi}{4} \tag{1}$

この公式を使うと、円周率を高精度で計算できることが知られています。具体的には、左辺の $\arctan$ のテイラー展開

$\displaystyle \arctan\frac{1}{5} = \sum_{n=0}^{\infty} (-1)^n \frac{\left(\frac{1}{5}\right)^{2n+1}}{2n+1}$

$\displaystyle \arctan\frac{1}{239} = \sum_{n=0}^{\infty} (-1)^n \frac{\left(\frac{1}{239}\right)^{2n+1}}{2n+1}$

を用いて、この級数の有限項を計算することで、高速に $\frac{\pi}{4}$ の値を計算できるのだそうです。

今日考えたいのは、マチンの公式はいったいどうやったら求められるのか？ということについてです。

マチンの公式の求め方については、以下の記事で紹介したことがありました。
tsujimotter.hatenablog.com

上の記事の議論はずいぶんと難解なものでしたが、今回はもう少し易しく紹介できるかと思います。

そして、そこには 239 という数の、ある興味深い性質が関わっていたのでした。

実際にマチンの公式の候補を求めるにあたっては、なんと一つ前の記事で投稿したペル方程式が関わってきます。いったいどこにペル方程式が出てくるというのでしょうか？

参考記事
今回の記事を執筆するにあたって、山田智宏さんの次の記事を参考にしています。
http://www41.tok2.com/home/tyamada1093/Stormer-j.htmlwww41.tok2.com

以前からマチンの公式に関心を持って勉強しておりましたが、特にStørmerの1897年論文の詳細が理解できませんでした。こちらの解説を読んでようやく理解することができました。山田さんありがとうございます。

山田さんの記事と重複する部分は多いかと思いますが、大変面白い内容なのでぜひ私の言葉でも紹介したいと思い、今回の記事を執筆しています。

マチン型の公式の作り方

マチンの公式を一般化した次の式を考えたいと思います：

$\displaystyle m\arctan\frac{1}{x} + n\arctan\frac{1}{y} = k\frac{\pi}{4} \tag{2}$

このような公式をマチン型の公式といいます。

特に

$m = 4, \; n = -1, \; x = 5, \; y = 239, \; k = 1$

のときがマチンの公式に一致します。

これから式 $(1)$ を満たす、整数 $m, n, x, y, k$ を見つけたいと思います。

まず、 $\arctan \frac{1}{x}$ ですが、これは2次元平面上の点 $(x, 1)$ が横軸に対してなす角として捉えることができます。図に表すとこうですね：

$\arctan \frac{1}{y}$ も同様に点 $(y, 1)$ のなす角として捉えることができます。

よって式 $(2)$ は、点 $(x, 1)$ のなす角を $m$ 倍して、点 $(y, 1)$ のなす角の $n$ 倍を足すと、 $\frac{\pi}{4}$ （45度）の $k$ 倍になると言っているわけですね。これもやはり図に書いた方がわかりやすそうです。

これまで2次元平面で考えてきましたが、複素数平面で考えるとより議論を進めることができます。

2次元平面で $(x, 1)$ ということは、複素数平面で $x+i$ に対応します。同様に $(y, 1)$ は $y+i$ に対応します。また、 $(x, 1), (y, 1)$ が横軸となす角は、複素数の偏角 $\arg(x+i), \; \arg(y+i)$ にそれぞれ対応します。

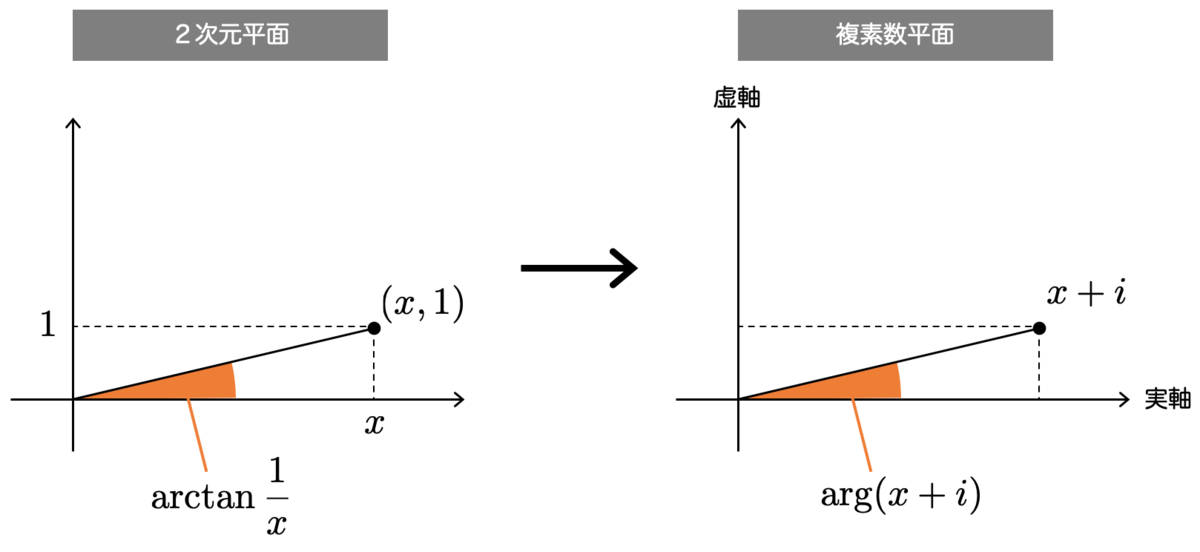
よって、複素数の偏角を使うと式 $(2)$ は

$\displaystyle m\arg(x+i) + n\arg(y+i) = k\arg(1+i) \tag{2}$

と表せますね。ここで、 $\arg(1+i) = \frac{\pi}{4}$ を使いました。

複素数の偏角については、変数の乗法が加法に、べき乗が乗法にそれぞれ置き換わるので、左辺と右辺はそれぞれ

$\displaystyle m\arg(x+i) + n\arg(y+i) = \arg (x+i)^m (y+i)^{n}$

$\displaystyle k\arg(1+i) = \arg (1+i)^k$

ということになります。したがって、式 $(2)$ は

$(x+i)^m (y+i)^{n}$ の偏角 $=$ $(1+i)^k$ の偏角

を意味します。言い換えると、ある正の実数 $r$ を用いて

$\displaystyle (x+i)^m (y+i)^{n} = r(1+i)^k \tag{3}$

が成り立つということと同値ですね。

ここまでマチン型の公式 $(1)$ が得られる条件について、同値な変形を続けてきました。したがって、式 $(3)$ を満たす複素数の積の組み合わせを見つけよう、ということになります。

ここで、複素数 $x+i, \; y+i, \; 1+i$ のそれぞれ共役をとって掛け合わせると $x^2+1, \; y^2+1, \; 2$ となります。

$(x^2+1)^m (y^2 + 1)^n = 2^k \tag{4}$

となるような組み合わせを見つけたら、再度式 $(3)$ に当てはめてうまくいくか確認するという方法が考えられます。

このようにして得られた $x, y, m, n, k$ からマチン型の公式 $(1)$ が得られるというわけです。

効率的に組み合わせを見つけるために、あらかじめ $x^2 + 1$ 型の数の素因数分解の一覧を考えておこうというのがアイデアです。 $x^2 + 1, \; y^2 + 1$ の素因数が差し引き $2^k$ になるような組み合わせを見つければよいわけですね。

まず、 $x^2 + 1$ に $x = 1, 2, 3$ を代入してみると

$1^2 + 1 = 2$
$2^2 + 1 = 5$
$3^2 + 1 = 2\cdot 5$

となりますね。 $(2\cdot 5) \cdot 5^{-1} = 2$ なので、ここからただちに

$(3^2 + 1)^1 (2^2 + 1)^{-1} = (1^2 + 1)^1$

が得られますね。

あとは、これを式 $(3)$ に当てはめて計算します。 $\{x+i, \; x-i\}$ 、 $\{y+i, \; y-i\}$ からそれぞれ１つ選んだ組み合わせが正解となります。実際

$\displaystyle \begin{align} \frac{3+i}{2+i} &= \frac{(3+i)(2-i)}{2^2+1} = \frac{7+i}{5} \\ \frac{3+i}{2-i} &= \frac{(3+i)(2+i)}{2^2+1} = \frac{5+5i}{5} = 1+i \end{align}$

となるので、下の方が正解ですね。よって

$\displaystyle (3+i)(2-i)^{-1} = 1+i$

となります。偏角をとると、 $\arg(2-i)^{-1} = \arg(2+i)$ より

$\displaystyle \arg(3+i)(2+i) = \arg(1+i)$

となります。左辺をばらすと

$\displaystyle \arg(3+i) + \arg(2+i) = \arg(1+i)$

となり、これがマチン型の公式

$\displaystyle \arctan\frac{1}{3} + \arctan\frac{1}{2} = \frac{\pi}{4} \tag{5}$

を導きます。

こんな要領で、どんどんと公式を見つけていくことができます。

$x^2 + 1$ の素因数分解について、他にもいくつか計算してみましょう。

$1^2+1 = 2^1$
$2^2+1 = 5^1$
$3^2+1 = 2^1 \cdot 5^1$
$4^2+1 = 17^1$
$5^2+1 = 2^1 \cdot 13^1$
$6^2+1 = 37^1$
$7^2+1 = 2^1 \cdot 5^2$
$8^2+1 = 5^1 \cdot 13^1$
$9^2+1 = 2^1 \cdot 41^1$
$10^2+1 = 101^1$

$\;\;\;\;\; \vdots$

$239^2+1 = 2^1 \cdot 13^4$

ここで、色をつけたところについて、素因数を揃えて観察します。

$\begin{align} 1^2+1 &= 2^1 & \\ 5^2+1 &= 2^1 \cdot & 13^1 \\ 239^2+1 &= 2^1 \cdot & 13^4 \end{align}$

すると

$\displaystyle (5^2 + 1)^4 (239^2 + 1)^{-1} = (1^2+1)^3$

が成り立つことがわかりますね。

あとは、 $(5+i)$ か $(5-i)$ 、 $(239+i)^{-1}$ か $(239-i)^{-1}$ を掛け算して計算すれば良いでしょう。実際

$(5+i)^4 (239+i)^{-1} = 2 + 2i = 2(1+i)$

が成り立ちますので、これを使えば良さそうです。

ここから偏角をとって $\arctan$ に置き換えれば

$\displaystyle 4\arctan\frac{1}{5} - \arctan \frac{1}{239} = \frac{\pi}{4} \tag{1再掲}$

が得られます。これがマチンの公式だったというわけですね。

以上は、 $\arctan$ の項が2項の場合のマチン型の公式についてのお話でしたが、これは多項バージョンの公式に一般化することができます。

たとえば、 $x^2 + 1, \; y^2 + 1, \; z^2 + 1$ としてうまく成立する組み合わせを作れば、3項バージョンのマチン型の公式を得ることができますね。同様に、変数の数はいくらでも増やすことができます。

x²+1 の素因数分解と 239 の出どころ

結局、マチンの公式のポイントは

$239^2 + 1$ という数が $2, 13$ という小さい素数だけで構成されていた

ことに尽きます。

そこで気になってくるのは、小さい素数だけで構成される $x^2 + 1$ は他にどれぐらいあるのか、という問題です。

まず注目したいポイントとしては、 $x^2 + 1$ の素因数としては、 $2$ か $4n+1$ 型の素数しか現れないということです。これは比較的簡単に証明できます。

（証明）
$x^2 + 1$ の任意の素因数を $p$ とする。このとき

$x^2 + 1 \equiv 0 \pmod{p}$

が成り立つ。移項して

$x^2 \equiv -1 \pmod{p}$

となる。

平方剰余の第１補充則より $p = 4n+3$ 型であれば $-1$ は平方非剰余であり、上の合同式は整数解 $x$ を持たない。

よって $p$ は $2$ または $4n+1$ 型である。

（証明終わり）

以上の議論から、素因数の候補としては $2, 5, 13$ の３つだけに限定して、これ以外に素因数を持たない $x^2 + 1$ を考えてみたいと思います。

プログラムを使って $x < 1000$ の範囲を調べてみましょう。すると、次の $9$ 個が発見されます：

$1^2+1 = 2^1$
$2^2+1 = 5^1$
$3^2+1 = 2^1 \cdot 5^1$
$5^2+1 = 2^1 \cdot 13^1$
$7^2+1 = 2^1 \cdot 5^2$
$8^2+1 = 5^1 \cdot 13^1$
$18^2+1 = 5^2 \cdot 13^1$
$57^2+1 = 2^1 \cdot 5^3 \cdot 13^1$
$239^2+1 = 2^1 \cdot 13^4$

意外と少ないですね！　というか、 $239^2 + 1$ 以降の数が一切登場していませんね！

それもそのはず。なんと、次のようなびっくりする事実が成り立ちます！

定理1

$13$ 以下の素因数しか持たない $x^2 + 1$ の中で最大のものは $239^2 + 1$ である

逆に言えば、 $240$ 以上の $x$ においては、 $x^2 + 1$ の素因数に必ず $17$ 以上の素因数が含まれてしまうというのです。

とても不思議ですね。いったいどうやって証明したら良いでしょうか。

そこで使えるのが、なんとペル方程式なのです！！

ペル方程式に帰着する

ペル方程式の解法を使うので「自信ないよ」という方は一つ前の記事を参照してください：
tsujimotter.hatenablog.com

ただし、全部読まなくても、今回の内容を理解する目的においては、以下の3点を思い出してもらえれば十分です：

① $D$ を平方数でない正の整数としたとき、 $x^2 - Dy^2 = \pm 1$ の形の方程式をペル方程式という。

② $\sqrt{D}$ の連分数展開の周期を $n$ としたとき、 $n-1$ 次近似分数を $P/Q$ とする。このとき、 $(x, y) = (P, Q)$ が $x^2 - Dy^2 = (-1)^n$ の整数解となる。 $n$ が偶数のとき右辺は $+1$ 、 $n$ が奇数のとき右辺は $-1$ 。特に、この解は最小解となっている。

③ペル方程式の解法を実行するのに、下記の連分数を計算するページが便利。
tsujimotter.info

それでは、問題設定をペル方程式の形に近づけていきましょう。

問題を整理すると、3つの素数 $2, 5, 13$ だけで構成されるような $x^2 + 1$ をすべて列挙したいわけですね。この条件を書き直すと、 $x^2 + 1$ という整数が

$x^2 + 1 = 2^{e_1} \cdot 5^{e_2} \cdot 13^{e_3} \tag{6}$

のように素因数分解できる、ということです。ここで $e_1, e_2, e_3$ は $0$ 以上の整数とします。

ここで、指数 $e_i$ を

$e_i = m_i + 2n_i \tag{7}$

という形で表したいと思います。 $m_i, n_i$ の取り方ですが、 $e_i$ の偶奇によって場合分けします：

$e_i$ が奇数の場合は $2$ で割ったあまりが $1$ である。あまりをとって $m_i = 1$ とする
$e_i$ が偶数の場合は $2$ で割ったあまりが $0$ である。もし $e_i = 0$ ならば $m_i = 0$ 、 $e_i > 0$ ならば $m_i = 2$ とする

要するに「 $e_i$ を $2$ で割ったあまり」を $m_i$ としているわけですね。偶数の場合はちょっと変わっていますが、このような処理をしておくことで、

$n_i > 0\;\; \text{ならば} \;\; m_i > 0 \tag{8}$

が常に成立することになります。

対偶をとって $m_i = 0\;\; \text{ならば} \;\; n_i = 0$ と言い換えると、これが成り立つことはすぐわかるかと思います。

実際、 $m_i = 0$ ならば $e_i = 0$ なので、 $2n_i = e_i - m_i = 0$ が成り立ちますね。

このように指数を設定しておいて、次のような変形をします：

$\begin{align} x^2 + 1 &= 2^{e_1} \cdot 5^{e_2} \cdot 13^{e_3} \\ &= 2^{m_1+2n_1} \cdot 5^{m_2+2n_2} \cdot 13^{m_3+2n_3} \\ &= (2^{m_1} \cdot 5^{m_2} \cdot 13^{m_3})\cdot (2^{n_1} \cdot 5^{n_2} \cdot 13^{n_3})^2 \end{align}$

最後の結果を移項すると

$x^2 - (2^{m_1} \cdot 5^{m_2} \cdot 13^{m_3})\cdot (2^{n_1} \cdot 5^{n_2} \cdot 13^{n_3})^2 = -1 \tag{9}$

となりますね。ここで

$D = 2^{m_1} \cdot 5^{m_2} \cdot 13^{m_3}$ 、 $y = 2^{n_1} \cdot 5^{n_2} \cdot 13^{n_3}$

と置けば

$x^2 - D y^2 = -1 \tag{10}$

となり、これはまさにペル方程式（の右辺が $-1$ になったもの）ですね！

また、 $D = 2^{m_1} \cdot 5^{m_2} \cdot 13^{m_3}$ については、指数の取り方から $m_i = 0, 1, 2$ のいずれかにしかならないのでした。

したがって、 $(m_1, m_2, m_3)$ のすべての組に対してペル方程式を考えて、それらを解いた後に、上の議論を逆にたどって $x^2 + 1$ の候補が得られるというわけです。

もちろん、このようにして得られたペル方程式の整数解のすべてが候補というわけではありません。
（ペル方程式は無限に整数解があるので、このままでは全然絞り込めません。）

そこで最小解に着目します。ペル方程式 $x^2 - Dy^2 = -1$ の最小解とは、正の整数の組 $(x, y)$ であって、 $y$ が最小のものを言います。

ここで次のような最小解の判定法を用います：

定理2

$(x, y)$ をペル方程式 $x^2 - Dy^2 = -1$ の正の整数解としたとき、次が成り立つ：

$y$ のすべての素因数が $D$ を割り切る $\; \Longrightarrow \;$ $(x, y)$ は最小解

今回はこれを認めて使います。

たとえば、証明はこちらに載っています（Proof of Theorem 2.）。
https://kam.mff.cuni.cz/~klazar/stormer.pdf

先ほどのペル方程式

$x^2 - (2^{m_1} \cdot 5^{m_2} \cdot 13^{m_3})\cdot (2^{n_1} \cdot 5^{n_2} \cdot 13^{n_3})^2 = -1 \tag{9再掲}$

$x^2 - D y^2 = -1 \tag{10再掲}$

において、 $n_i > 0$ ならば $m_i > 0$ が成り立つのでした。これは $y$ のすべての素因子が $D$ を割り切ることを意味しますね。

よって、我々が求めたい解を得るためには、ペル方程式の最小解を調べれば十分であったということになります。

したがって、次のような手順で $2, 5, 13$ のみを素因数に持つ $x^2 + 1$ がすべて列挙できると分かります：

$(m_1, m_2, m_3)$ のすべての組に対して $D = 2^{m_1} \cdot 5^{m_2} \cdot 13^{m_3}$ を計算する
対応するペル方程式 $x^2 - Dy^2 = -1$ の最小解 $(x, y)$ を求める（解を持たない場合もある）
最小解が得られたら、移項して $x^2 + 1 = Dy^2$ を得る。右辺の素因数が $2, 5, 13$ のみであるかどうか確認する

上記の $(m_1, m_2, m_3)$ の候補はもう少し絞り込むことができます。

たとえば $D$ が平方数である場合は考える必要がありません。それは次の理由からです。

$D = d^2$ としておくと、方程式は

$x^2 - (dy)^2 = -1$

となります。 $dy$ を $x$ 、 $x$ を $y$ と改めて置きなおすと

$x^2 - y^2 = 1$

となります。この解は、左辺を因数分解し、右辺の約数 $\pm 1$ と比較することで、解が $(x, y) = (\pm 1, 0)$ のみであるとわかります。よって、ここから目的の $x^2 + 1$ は得られません。

さらに、 $2$ の指数 $e_1$ については、 $0, 1$ のいずれかにしかならないことも分かります。それは次の理由からです。

平方数を $4$ で割ったあまりは、偶奇を考えることで $0, 1$ のいずれかしかとらないことがわかります。よって

$x^2 + 1 \equiv 1, 2 \pmod{4}$

となります。したがって、 $x^2 + 1$ が $2^2$ で割り切れることはありません。

これでだいぶ候補が絞り込めました。そんなわけで、 $D$ のパターンとしては以下の 14通りを考えればよいことになります：

$D_1 = 2^1 5^0 13^0 = 2$
$D_2 = 2^0 5^1 13^0 = 5$
$D_3 = 2^1 5^1 13^0 = 10$
$D_4 = 2^1 5^2 13^0 = 50$
$D_5 = 2^0 5^0 13^1 = 13$
$D_6 = 2^1 5^0 13^1 = 26$
$D_7 = 2^0 5^1 13^1 = 65$
$D_8 = 2^1 5^1 13^1 = 130$
$D_9 = 2^0 5^2 13^1 = 325$
$D_{10} = 2^1 5^2 13^1 = 650$
$D_{11} = 2^1 5^0 13^2 = 338$
$D_{12} = 2^0 5^1 13^2 = 845$
$D_{13} = 2^1 5^1 13^2 = 1690$
$D_{14} = 2^1 5^2 13^2 = 8450$

14個のペル方程式を解く

前回の記事で述べたように、ペル方程式 $x^2 - D_i y^2 = -1$ の正の整数解は、 $\sqrt{D_i}$ の連分数展開の周期 $n$ が奇数のとき $n-1$ 次近似分数によって得られます。特に、この方法によって得られる解はペル方程式の最小解となっています。

そんなわけで、連分数展開をひたすら計算して、上記のペル方程式14個の最小解を順に計算していきましょう。なお、あとで具体例で述べるように周期が偶数のときは $x^2 - D_i y^2 = -1$ の整数解は存在しませんので、その点は注意する必要があります。

2021.03.03追記　最小解についての言及を追記しました。

$D_1 = 2$ の場合について考えましょう。 $\sqrt{2}$ の連分数展開を計算すると

$\displaystyle \sqrt{2} = 1 + \cfrac{1}{2 + \cfrac{1}{2 + \cfrac{1}{2 + \cfrac{1}{2 + \cfrac{1}{\ddots}}}}}$

となりますね。周期は $1$ なので、 $0$ 次の近似分数を考えると

$\displaystyle 1 = \frac{1}{1}$

となり、 $(x, y) = (1, 1)$ が $x^2 - 2y^2 = -1$ の最小解となります。

連分数展開は、次のアプリで計算すればすぐ求まりますね！
tsujimotter.info

同様に、 $D_2 = 5$ の場合を考えましょう。 $\sqrt{5}$ の連分数展開を計算すると

$\displaystyle \sqrt{5} = 2 + \cfrac{1}{4 + \cfrac{1}{4 + \cfrac{1}{4 + \cfrac{1}{4 + \cfrac{1}{\ddots}}}}}$

となりますね。周期は $1$ なので、 $0$ 次の近似分数を考えると

$\displaystyle 2 = \frac{2}{1}$

となり、 $(x, y) = (2, 1)$ が $x^2 - 5y^2 = -1$ の最小解となります。

どんどんいきましょう。 $D_3 = 10$ の場合です。 $\sqrt{10}$ の連分数展開を計算すると

$\displaystyle \sqrt{10} = 3 + \cfrac{1}{6 + \cfrac{1}{6 + \cfrac{1}{6 + \cfrac{1}{\ddots}}}}$

となりますね。周期は $1$ なので、 $0$ 次の近似分数を考えると

$\displaystyle 3 = \frac{3}{1}$

となり、 $(x, y) = (3, 1)$ が $x^2 - 10y^2 = -1$ の最小解となります。

あんまりおもしろいものが出てこないので、一つ飛ばして $D_{5} = 13$ を考えます。 $\sqrt{13}$ の連分数展開を計算すると

$\displaystyle \sqrt{13} = 3 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{6 + \cfrac{1}{\ddots}}}}}}$

となります。分かりにくいですが、 $1, 1, 1, 1, 6$ までが周期となり、周期の長さは $5$ です。よって、 $4$ 次の近似分数を考えると

$\displaystyle 3 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1}}}} = \frac{18}{5}$

となり、 $(x, y) = (18, 5)$ が $x^2 - 13y^2 = -1$ の最小解となります。

例外的なケースとして $D_{10} = 650$ を考えておきましょう。 $\sqrt{650}$ の連分数展開を計算すると

$\displaystyle \sqrt{650} = 25 + \cfrac{1}{2 + \cfrac{1}{50 + \cfrac{1}{2 + \cfrac{1}{50 + \cfrac{1}{\ddots}}}}}$

となります。周期は $2$ なので今回は偶数です。この場合は、右辺が $-1$ である解を持たないことが知られています。連分数では、 $1$ 次近似分数を計算すると

$\displaystyle 25 + \cfrac{1}{2} = \frac{51}{2}$

となるので、 $(x, y) = (51, 2)$ が右辺が $+1$ となるペル方程式 $x^2 - 650y^2 = 1$ の最小解となります。これ以外を探しても、 $-1$ の解は存在しません。

もう一つだけ、 $D_{11} = 338$ を計算させてください。これだけはどうしても計算したいのです。 $\sqrt{338}$ の連分数展開を計算すると

$\displaystyle \sqrt{338} = 18 + \cfrac{1}{2 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{2 + \cfrac{1}{36 + \cfrac{1}{\ddots}}}}}}$

となります。 $2, 1, 1, 2, 36$ までが周期となり、周期の長さは $5$ です。よって、 $4$ 次の近似分数を考えると

$\displaystyle 18 + \cfrac{1}{2 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{2}}}} = \frac{239}{13}$

となり、 $(x, y) = (239, 13)$ が $x^2 - 338y^2 = -1$ の最小解となります。

さぁ、私がどうしても計算したかった理由がわかったでしょうか。ついに、 $239$ が出てきましたね！！

そんなわけで、同様の方法で $D_1$ から $D_{14}$ の連分数を計算していき、右辺が $-1$ となる最小解を持つもの（周期が奇数のもの）だけを集めると、次のようになります：

$1^2 - 2\cdot 1^2 = -1$ 　（周期 $1$ ）
$2^2 - 5\cdot 1^2 = -1$ 　（周期 $1$ ）
$3^2 - 10\cdot 1^2 = -1$ 　（周期 $1$ ）
$7^2 - 50\cdot 1^2 = -1$ 　（周期 $1$ ）
$18^2 - 13\cdot 5^2 = -1$ 　（周期 $5$ ）
$5^2 - 26\cdot 1^2 = -1$ 　（周期 $1$ ）
$8^2 - 65\cdot 1^2 = -1$ 　（周期 $1$ ）
$57^2 - 130\cdot 5^2 = -1$ 　（周期 $3$ ）
$18^2 - 325\cdot 1^2 = -1$ 　（周期 $1$ ）
$239^2 - 338\cdot 13^2 = -1$ 　（周期 $5$ ）
$12238^2 - 845\cdot 421^2 = -1$ 　（周期 $5$ ）
$54608393^2 - 8450\cdot 594061^2 = -1$ 　（周期 $13$ ）

これらの結果を移項すると、次のようになります。

$1^2 + 1 = 2\cdot 1^2 = 2^1$
$2^2 + 1 = 5\cdot 1^2 = 5^1$
$3^2 + 1 = 10\cdot 1^2 = 2^1 \cdot 5^1$
$7^2 + 1 = 50\cdot 1^2 = 2^1 \cdot 5^2$
$18^2 + 1 = 13\cdot 5^2 = 5^2\cdot 13^1$
$5^2 + 1 = 26\cdot 1^2 = 2^1 \cdot 13^1$
$8^2 + 1 = 65\cdot 1^2 = 5^1 \cdot 13^1$
$57^2 + 1 = 130\cdot 5^2 = 2^1 \cdot 5^3 \cdot 13^1$
$18^2 + 1 = 325\cdot 1^2 = 5^2 \cdot 13^1$
$239^2 + 1 = 338\cdot 13^2 = 2^1 \cdot 13^4$
$12238^2 + 1 = 845\cdot 421^2 = 5^1 \cdot 13^2 \cdot \mathbf{421}^2$
$54608393^2 + 1 = 8450\cdot 594061^2 = 2^1 \cdot 5^2 \cdot 13^3 \cdot \mathbf{45697}^2$

$12238^2 + 1, \; 54608393^2 + 1$ のところに $17$ 以上の素数が出ていますが、これは想定内です。上記の解はペル方程式の最小解ですが、定理1の条件は、

$y$ のすべての素因数が $D_i$ を割り切る $\; \Longrightarrow \;$ $(x, y)$ は最小解

なのでした。逆は必ずしも真ではないというわけですね。

大事なことは、上で挙げた解ですべて尽くされているということです。図で表すとこんな感じになります。

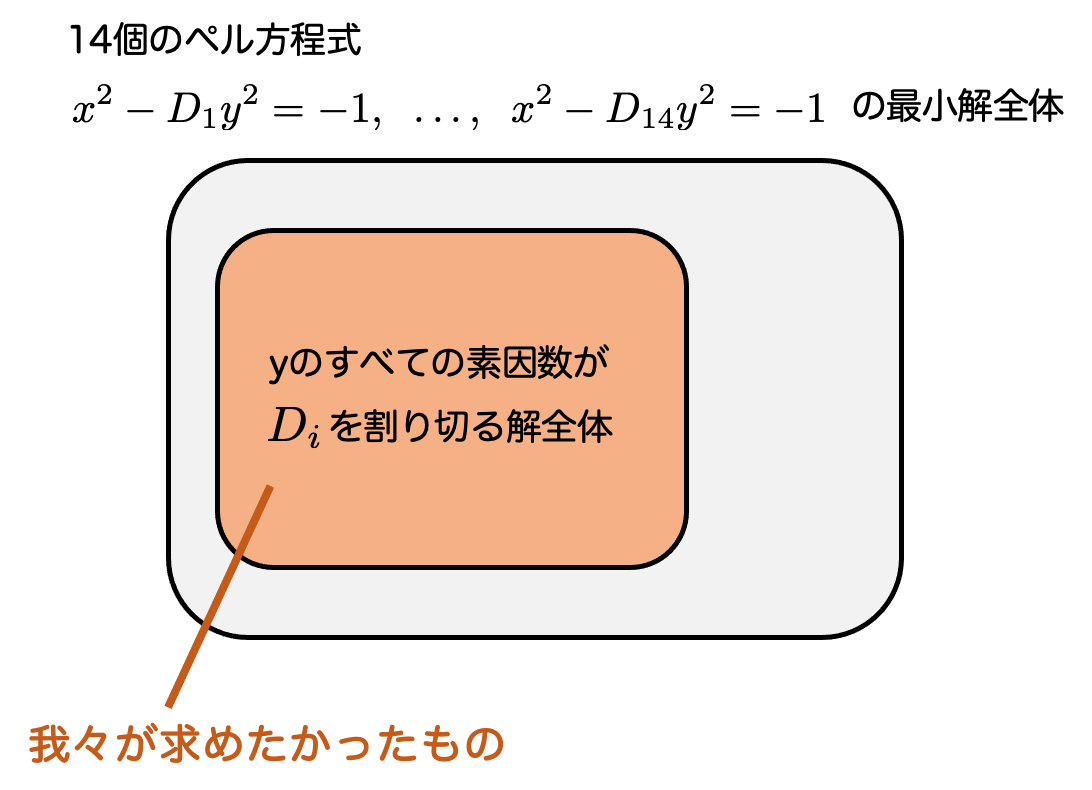
我々が求めたかった解（ $2, 5, 13$ だけを素因数に持つ $x^2 + 1$ のリスト）は、図のオレンジ色の領域であり、上で挙げた14個のペル方程式の最小解のリストの中に含まれているということですね。

よって、 $2, 5, 13$ だけを素因数に持つ $x^2 + 1$ は、上記で挙げたものしか存在しないということが示されました。たしかに、 $18^2 + 1$ の重複を除けば、プログラムで $x < 1000$ まで計算した $9$ 個がすべて列挙されていますね。あれで全部だったというわけです！