リュカのキャノンボール問題 - tsujimotterのノートブック

面白い問題を見つけたので紹介します！

「エドゥアール・リュカ」という名前を聞いたことがあるでしょうか。リュカ数列や，メルセンヌ素数の「リュカ・レーマーテスト」で有名なあの「リュカ」です。
彼は数学にまつわるパズルのような問題をたくさん紹介したことで知られていますね。

「ハノイの塔」というパズルもリュカが最初に紹介したものです。

CC 表示-継承 3.0, https://commons.wikimedia.org/w/index.php?curid=228623

さて，今日お話したいのは，そのリュカが考察したことで知られる

「キャノンボール問題」

です。

キャノンボール問題は，以下の方程式の整数解 $(n, M)$ をすべてみつけよ，というディオファントス問題の一種です。

$\displaystyle \sum_{k=1}^{n} k^2 = M^2 \tag{1}$

キャノンボールとは

「キャノンボール」とは「砲丸」のことですが，その心は何なのでしょうか。

左辺を定義に従って書き直すとこうなりますね。

$\displaystyle 1^2 + 2^2 + 3^2 + \cdots + n^2 = M^2$

$1$ から $n$ までの平方数の和になっています。平方数とは，球体１つを "１" とみたときに，それらを "正方形" に並べてできる数ですね。

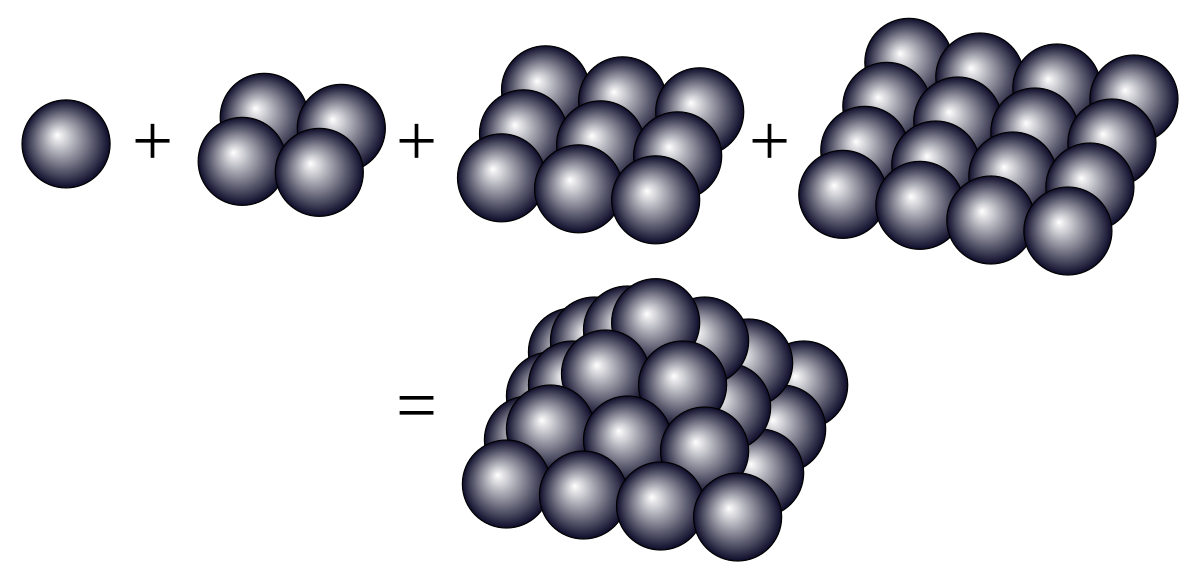
このことを思い浮かべながら以下の図を眺めます。

By David Eppstein at English Wikipedia - Transferred from en.wikipedia to Commons., Public Domain, https://commons.wikimedia.org/w/index.php?curid=2496784

平方数を重ねてできたピラミッドのつくる数が， $M^2$ ，すなわち平方数になるか？というのが元の問題だったというわけです。

ところでこの図形，砲丸をピラミッド状に並べているように見えてきませんか？

実際に，砲丸をならべてみた図も Wikipedia に載っていました。

By Ji-Elle - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=10051683

まさに「キャノンボール問題」ですね。きっとリュカも上のような図を頭に思い浮かべていたのでしょう。

別名「平方ピラミッド問題（Square Pyramid Problem）」とも言われるようです。そのまま過ぎですね。笑

個人的にはキャノンボールの方がセンスがあって好きです。

キャノンボール問題の解

さて，ではキャノンボール問題の解について考えていきましょう。これを読んでいるみなさんも，よかったらどんな解があるか考えてみましょう。

私は，いつものようにプログラム（Ruby）を使います。笑

すべての $n$ について調べるのは不可能なので，とりあえず $n \leq 1000$ の範囲で探索してみましょう。

# search_spn.rb 
# n=1000 以下の平方ピラミッド数(Square Pyramidal Number) を探索する

1000.times do |n|

    sum = 0
    (1..n).each do |k|
        sum += k*k
    end

    sqrt       = Math.sqrt(sum)
    sqrt_floor = Math.sqrt(sum).floor


    if sqrt == sqrt_floor then
        # sum is square number

        m = sqrt.to_i
        puts "n = #{n}, M = #{m}"
    end

end

このプログラムを実行すると， $\sum_{k=1}^{n} k^2 = M^2$ を満たすような，整数解 $(n, M)$ の組が $0\leq n \leq 1000$ の範囲で見つかります。

実行結果は次の通りです。

$ ruby search_spn.rb 
n = 0, M = 0
n = 1, M = 1
n = 24, M = 70

３組見つかりました！

$n = 0, 1$ のときは自明ですね。

面白いのは $n = 24$ のときです。

$1^2 + 2^2 + 3^2 + \cdots + 24^2 = 4900 = 70^2$

となって，たしかにキャノンボール問題の解になることがわかりますね。

今回は $n \leq 1000$ の範囲で探索しましたが，他に解は存在しないのでしょうか。

$n \leq 10000$ としても解は見つかりません。私はやっていませんが，実はこの先ずっと探しても見つからないのです。

プログラムの便利なところは，ある程度の範囲までは力づくで解を見つけてくれることです。その反面，解がもう存在しないことを示すことは難しいです。
これ以上解がないことを，いったいどうやって示せば良いのでしょうか。

歴史的なことを話すと，リュカは 1875 年にこの問題を発案し，非自明な解として $(24, 70)$ を見つけていました。この他に非自明な解が存在しないことを示唆していたようですが，証明には至りませんでした。

1918 年に Watson *1 がこの問題に完全な解を与えました。すなわち，これ以上非自明な解が存在しないことを示したのです。その方法は modulus が $1/\sqrt{2}$ である楕円関数を用いた非常に複雑な証明とのことです。なかなか興味を惹かれる内容ですが，私は彼の文献を見つけることができませんでした。