一昨日の RSA 暗号の記事で、オイラー関数 という関数が登場しました。暗号理論に限らず、整数論においてとても大事な関数となっていますので、ちょっと補足したいなと思いました。
特に、関数の引数が「２つの素数の積」となる場合の説明をまったくしていなかったので、それについてまとめたいと思います。
まずは、何はともあれ定義から再掲しましょう。
オイラー関数の定義：
より小さい正の整数で
と書いて，これをオイラー関数と呼ぶ．
に具体的な数字を入れて考えてみましょう。
のとき
この例は、前の記事にも書きましたが、おさらいとしてもう一度書きましょう。
より小さい正の整数は次の
個です。
ここで、 は
と素因数分解されますから、素因数である
と
を約数に持つかどうか考えれば良いですね。
を約数に持つ数は
の
個、一方
を約数に持つ数は
の
個だけです。したがって、これらを引いた残りの
個が
と互いに素な数となります。一応列挙すると、
結局、 ですね。
これを図にするとこんな感じになります。
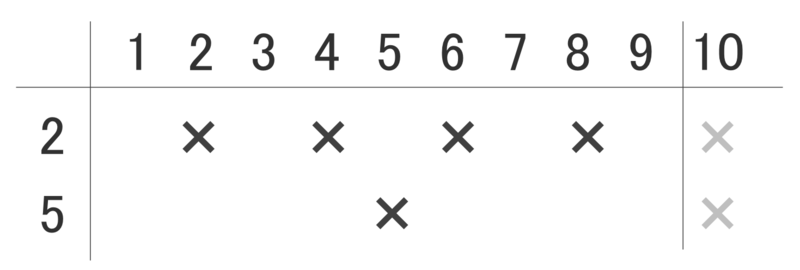
ちなみに、重要なポイントですが、 と
に対して、それぞれの×の位置が重ならないことに注意してください。
が素数のとき
より小さい数は
の
個です。
さぁ、ここで問題です。これらの数の中で、素数 と互いに素な数はどれでしょう？
・・・
もちろん、すべてですね。笑
と互いに素、すなわち、
と
以外の公約数を持つためには、（
が素数より）
の倍数にならなければいけませんが、そうなるためには
より大きくなければいけません。上に挙げた数はすべて
より小さい数なので、それはありえませんね。したがって、すべて互いに素な数になります。
よって、 となります。
一昨日の記事で述べた通り、 が素数であるときは、フェルマーの小定理と関連しますから、この結果は非常に重要です。
が２つの素数の積で表される数のとき
さて、最後です。 が
という２つの素数の積で表される数のときを考えましょう。すなわち、
この状況は、RSA 暗号で重要な役割を果たしましたね。
さて、先ほどと同様に より小さい数を考えると、それは
ここで、 より、上で挙げた数が素因数
と
を約数に持つかを考えます。
を素因数に持たない数が、私たちが求める
と互いに素な数です。
イメージしやすいように ,
としたときの例を図にしてみましょう。
です。
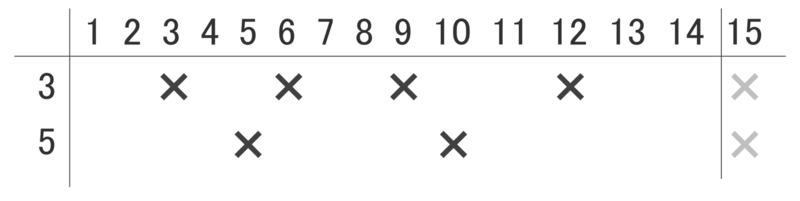
を素因数に持つ数は
の倍数です。したがって、
より小さい
の倍数は、
となります。これは、全部で 個です。（図の例では
となってたしかに合っていますね。）
一方で、 を素因数に持つ数は
の倍数です。したがって、
より小さい
の倍数は、
の 個です。（同様に、図の例では
となって、ちゃんと合致しています。）
ここでポイントとなるのは、それぞれの約数が重ならない、という点です。もし重なる数が存在するとしたら「 の倍数，かつ，
の倍数」ということになります。したがって、こういった数は 「
の最小公倍数の倍数」となるはずです。
の最小公倍数は
ですが、
より小さい数のリストにそのような数は存在しません。
したがって、結局 以下の数で
と互いに素になる数の個数は、全体の個数
から
,
を引いた数になりますね。よって
となります。つまり
となって目的の式が得られました。
一応、,
を入れて確かめてみると、
となります。図のリストの中から、×がついていない数を並べると、
の 個ですから、ちゃんと一致していますね。あーよかった。
めでたし、めでたし。ということで、簡単ですが今日の記事を終わりたいと思います。それでは。
謝辞
のときの計算式の導出は、例の「RSA暗号について質問してきた知人」に教えてもらった方法です。オイラー関数の定義について tsujimotter が教えていると、「じゃあ合成数だったらこうなるね」と図を使って説明してくれたのでした。その導出方法があまりに美しかったので、そのインスピレーションをいただいて今回の記事となりました。知人に感謝です。
関連記事
一昨日のRSA 暗号に関する記事です。本記事はこちらの補足として書きました。
RSA 暗号がようやく分かった気がしたのでまとめてみる - tsujimotterのノートブック
