mod mのべき乗余が何通りの値を取るかという話

１つ前の記事に関連して「 $a^{k} \pmod{m}$ がどんな値をとるのか」という問題が気になりました。
tsujimotter.hatenablog.com

上の記事では

$k = \varphi(m)+1$ のとき $a^{\varphi(m)+1} \equiv a \pmod{m}$
$k = \lambda(m)+1$ のとき $a^{\lambda(m)+1} \equiv a \pmod{m}$

となる、つまり $a = 0, \ldots, m-1$ の全ての値を取ることを示しました。鯵坂もっちょさんの可視化の方法を用いるならば、右肩上がりの階段状になります。

f:id:tsujimotter:20210122201425p:plain:w400

（横軸が $a$ で、縦軸が $a^7 \pmod{42}$ となっています）

「 $a$ が $m$ と互いに素であるかどうかに関わらず」このようになるというのが面白かったわけですね。

一方で、 $k = \varphi(m)$ 乗した場合については、特に法則はなさそうに見えました。何か法則はあるのでしょうか。

そんなことを考えているうちに、青山学院大学の中川貴仁さんの卒論研究を見つけました。

整数のべき乗とオイラーの定理について
中川貴仁（西山研究室）
http://www.gem.aoyama.ac.jp/~kyo/sotsuken/2014/nakagawa_sotsuron_2014.pdf

中川さんの論文によると、 $m$ が相異なる $r$ 個の素数の積で表されるとき、すなわち

$m = p_1 p_2 \cdots p_r$

のとき、 $a^{\varphi(m)} \pmod{m}$ の値は $2^r$ 個通りの数をとるそうなのです。

$a$ が $m$ と互いに素のときは、オイラーの定理により $a^{\varphi(m)} \equiv 1 \pmod{m}$ ですから、常に $1$ の値をとります。上の話は、 $a$ が $m$ と互いに素とは限らないときも含めて、何パターンの値を取りうるかを教えてくれます。

そんなことが証明できるのですね。大変面白かったので、証明を紹介したいと思います。

証明

$m$ を相異なる2つの素数の積 $m = pq$ とします。（ $m = p_1 p_2 \cdots p_r$ のときも、まったく同じ流れで証明できますので、前回同様 $r = 2$ の場合だけ紹介します。）

$p \mid a$ かつ $q \mid a$ の場合を考えます。この場合 $a \equiv 0 \pmod{p}$ かつ $a \equiv 0 \pmod{q}$ なので

$\begin{cases} a^{\varphi(m)} \equiv 0 \pmod{p} \\ a^{\varphi(m)} \equiv 0 \pmod{q} \end{cases}$

が成り立ちます。つまり、 $X = a^{\varphi(m)}$ とおくと

$\begin{cases} X \equiv 0 \pmod{p} \\ X \equiv 0 \pmod{q} \end{cases}$

次に、 $p \not\mid a$ かつ $q \mid a$ の場合を考えます。この場合は、フェルマーの小定理より

$a^{p-1} \equiv 1 \pmod{p}$

が成り立ちます。これを両辺 $q-1$ 乗すると、指数が $\varphi(m) = (p-1)(q-1)$ になります。 $\bmod{q}$ の場合は、一個前と同様なので $X = a^{\varphi(m)}$ とおくと

$\begin{cases} X \equiv 1 \pmod{p} \\ X \equiv 0 \pmod{q} \end{cases}$

同様に、 $p \mid a$ かつ $q \not\mid a$ の場合は、 $X = a^{\varphi(m)}$ とおくと

$\begin{cases} X \equiv 0 \pmod{p} \\ X \equiv 1 \pmod{q} \end{cases}$

となり、 $p \not\mid a$ かつ $q \not\mid a$ の場合は、 $X = a^{\varphi(m)}$ とおくと

$\begin{cases} X \equiv 1 \pmod{p} \\ X \equiv 1 \pmod{q} \end{cases}$

が成り立ちます。

結局、 $a$ を $p, q$ が割り切るかどうかのパターンに応じて

$(X \bmod{p}, \; X \bmod{q}) \equiv (0, 0), \; (1, 0), \; (0, 1), \; (1, 1)$

の4通りの値を取ることになります。

ここで、中国剰余定理により、以上の4通りそれぞれに対して、 $X \pmod{pq}$ が一意的に定まり、しかも相異なる数となります。したがって、 $m = pq$ より $a^{\varphi} \pmod{m}$ は4通りの値を取る事が示されました。
（素因数の個数が $r$ 個の場合は $2^r$ 通り。）

（証明終わり）

なお、以上の4番目のケースが、 $a$ が $m = pq$ と互いに素な条件になっています。したがって、4通りの中に $1\pmod{m}$ は含まれるわけですね。

カーマイケルの定理に拡張

上の証明を見てみると、どうやらまたカーマイケルの定理に拡張ができそうです。
tsujimotter.hatenablog.com

カーマイケルの定理と $\lambda(m)$ については上の記事を読んでいただきたいと思います。今回の記事の証明中で、 $\varphi(m) = (p-1)(q-1)$ となっているところをすべて $\lambda(m) = \operatorname{LCM}(p-1, q-1)$ としてしまえば、 $\varphi(m)$ を $\lambda(m)$ にそのまま置き換えた定理が示されるわけですね。よって、次の事実が成り立ちます：

カーマイケル版 $a^{\lambda(m)}\bmod{m}$ の値の個数

$m$ が相異なる $r$ 個の素数の積で表されるとき、すなわち

$m = p_1 p_2 \cdots p_r$

のとき、 $a^{\lambda(m)} \pmod{m}$ の値は $2^r$ 個通りの数をとる

これを使うと、 $m = 42 = 2\cdot 3 \cdot 7$ で素因数の個数は $3$ です。 $\lambda(42) = 6$ であることから、 $a^6 \bmod{42}$ は $2^3 = 8$ 通りのパターンを取ることになります。

実際やってみると

$\{a^6 \pmod{42} \mid 0 \leq a \leq 41\} = \{0, 1, 22, 15, 36, 7, 28, 21\}$

となりました。たしかに8通りになっていますね！

鯵坂もっちょさんの可視化方法を使って確認してみるとこんな感じになります。

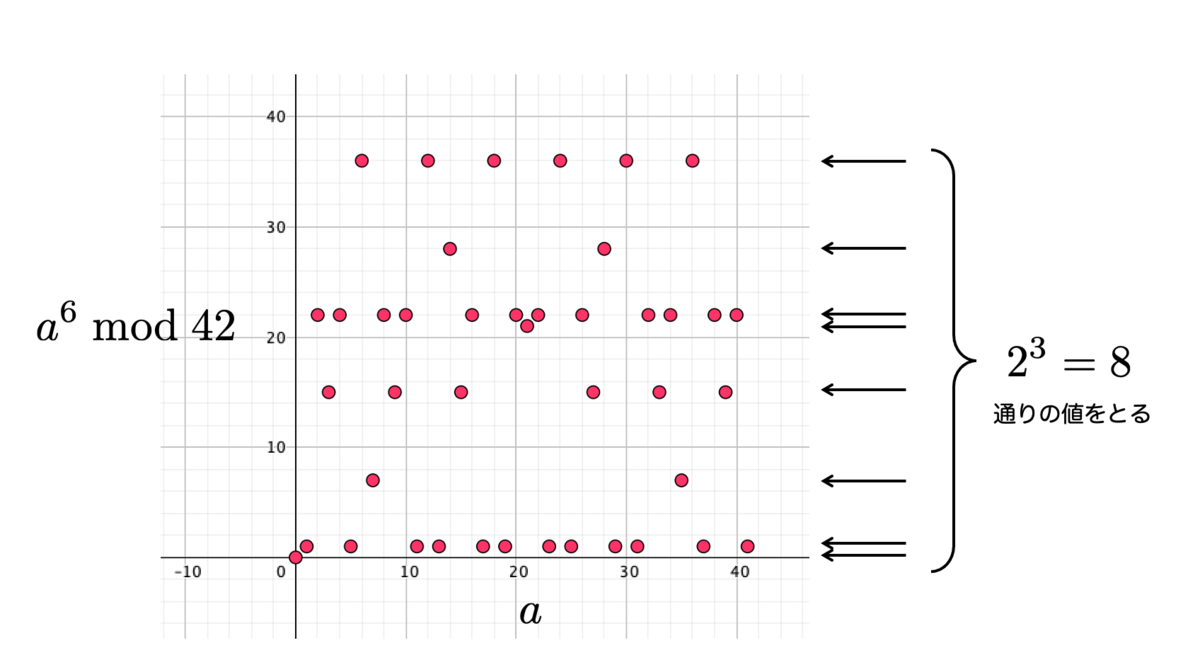
f:id:tsujimotter:20210122200945p:plain:w600

横軸は $a = 0, 1, \ldots, 41$ を取っていて、縦軸に $a^6\pmod{42}$ の値をとっています。たしかに、縦方向を数えると 8 通りの数が出ている事が確認できます。

これにさらにもう一回 $a$ をかけるだけで、

こんな風に直線になってしまうのだから mod の世界は面白いですね。これが互いに素とは限らない場合も含んだオイラーの定理の結果です。

それでは今日はこの辺で！

追記：一般の $m$ についての一般化

上では、 $m = p_1 p_2 \cdots p_r$ という特殊な形の $\bmod{m}$ について考えました。しかしながら、このような形に限定せずとも、一般の $m$ に対して拡張できる事に気づきました。

定理

$m$ を任意の2以上の整数とし、 $r$ を $m$ の相異なる素因数の個数とする。すなわち

$m = p_1^{e_1} p_2^{e_2} \cdots p_r^{e_r}$

のとき、 $a^{\varphi(m)} \pmod{m}$ （あるいは、 $a^{\lambda(m)} \pmod{m}$ ）の値は $2^r$ 個通りの数をとる

証明もほとんど同じです。例によって、素因数の個数が2個のパターン $m = p^e q^f$ だけで議論します。

（証明）
$m = p^e q^f$ とする。

$p \mid a$ かつ $q \mid a$ の場合を考えます。この場合 $a \equiv 0 \pmod{p}$ かつ $a \equiv 0 \pmod{q}$ です。

このとき $a = a' p$ とおき、 $\varphi(p^e) = p^{e-1}(p-1)$ を使う。すると

$\begin{align} a^{\varphi(p^e)} &= (a' p)^{\varphi(p^e)} \\ &= (a')^{\varphi(p^e)} \cdot p^{\varphi(p^e)} \end{align}$

ここで、 $e \geq 1$ であれば $e \leq p^{e-1}(p-1)$ ですから、全体は $p^e$ で割り切れます。したがって、

$a^{\varphi(p^e)} \equiv 0 \pmod{p^e}$

両辺を $\varphi(q^e)$ 乗すると $\varphi(m) = \varphi(p^e)\varphi(q^f)$ より

$a^{\varphi(m)} \equiv 0 \pmod{p^e}$

が成り立ちます。 $\bmod{q^f}$ のときも同様に考えると

$\begin{cases} a^{\varphi(m)} \equiv 0 \pmod{p^e} \\ a^{\varphi(m)} \equiv 0 \pmod{q^f} \end{cases}$

が成り立ちます。つまり、 $X = a^{\varphi(m)}$ とおくと

$\begin{cases} X \equiv 0 \pmod{p^e} \\ X \equiv 0 \pmod{q^f} \end{cases}$

次に、 $p \not\mid a$ かつ $q \mid a$ の場合を考えます。この場合は、オイラーの定理より

$a^{\varphi(p^e)} \equiv 1 \pmod{p^e}$

が成り立ちます。これを両辺 $\varphi(q^f)$ 乗すると、指数が $\varphi(m) = \varphi(p^e)\varphi(q^f)$ になります。 $\bmod{q^f}$ の場合は、一個前と同様なので $X = a^{\varphi(m)}$ とおくと

$\begin{cases} X \equiv 1 \pmod{p^e} \\ X \equiv 0 \pmod{q^f} \end{cases}$

同様に、 $p \mid a$ かつ $q \not\mid a$ の場合は、 $X = a^{\varphi(m)}$ とおくと

$\begin{cases} X \equiv 0 \pmod{p^e} \\ X \equiv 1 \pmod{q^f} \end{cases}$

となり、 $p \not\mid a$ かつ $q \not\mid a$ の場合は、 $X = a^{\varphi(m)}$ とおくと

$\begin{cases} X \equiv 1 \pmod{p^e} \\ X \equiv 1 \pmod{q^f} \end{cases}$

が成り立ちます。

結局、 $a$ を $p, q$ が割り切るかどうかのパターンに応じて

$(X \bmod{p^e}, \; X \bmod{q^f}) \equiv (0, 0), \; (1, 0), \; (0, 1), \; (1, 1)$

の4通りの値を取ることになります。

ここで、中国剰余定理により、以上の4通りそれぞれに対して、 $X \pmod{p^e q^f}$ が一意的に定まり、しかも相異なる数となります。したがって、 $m = p^e q^f$ より $a^{\varphi} \pmod{m}$ は4通りの値を取る事が示されました。
（相異なる素因数の個数が $r$ 個の場合は $2^r$ 通り。）

（証明終わり）

追記2：中国剰余定理

$m = p_1^{e_1} p_2^{e_2} \cdots p_r^{e_r}$ としたとき、環 $\mathbb{Z}/m\mathbb{Z}$ には次のような準同型写像があります：

$\begin{align} f\colon \mathbb{Z}/m\mathbb{Z} &\longrightarrow \mathbb{Z}/p_1^{e_1}\mathbb{Z} \times \mathbb{Z}/p_2^{e_2}\mathbb{Z} \times \cdots \times \mathbb{Z}/p_r^{e_r}\mathbb{Z}, \\ a\bmod{m} &\longmapsto (a\bmod{p_1^{e_1}}, \; a\bmod{p_2^{e_2}}, \; \ldots, \; a\bmod{p_r^{e_r}}) \end{align}$

これが環同型になっているというのが、中国剰余定理の言い換えになっています。

さて、本日数学デーに参加したときに「今回の問題はこの環同型を通して考えれば良い」ということを龍孫江さんに教えていただきました。

左側の $k$ 乗は、右側の環における $k$ 乗にそのまま対応します。したがって、 $\mathbb{Z}/p_i^{e_i}\mathbb{Z}$ の中で

$a^k \equiv 0, 1$

になることが言えれば、 $f$ による $A = \{a^k\bmod{m} \mid a \in \mathbb{Z}/m\mathbb{Z}\}$ の像が $\{0, 1\}^r$ になることがわかります。上の同型を逆に使って $\mathbb{Z}/m\mathbb{Z}$ に戻してくれば、 $\#A = 2^r$ 個になることがわかるというわけですね。