tsujimotterのノートブック

日曜数学者 tsujimotter の「趣味で数学」実践ノート

素イデアル分解法則を考える（ヒルベルトの理論とフロベニウス自己同型）

素数 数学 整数論 類体論

今日は私がまさに今現在勉強している「素イデアルの分解法則」についてお話ししたいと思います。

素イデアルの分解については，これまでの記事でも「フェルマーの二平方定理」やその関連する法則について触れてきましたので，ずっと興味はあったのです。しかしながら，個別ケースの調査にとどまっており，一般論にはいたっていませんでした。

一般的には「類体論」とよばれる理論があって，その系として上記の話は示されるそうです。「類体論までは踏み込まずとも，その手前ぐらい（具体的には「ヒルベルトの理論」くらいまで）は理解したい」そう思って，今まで斜め読みしかしていなかった専門書に本腰入れて取り組むことに決めました。*1

ようやくその正体がわかってきて，先日は「フロベニウス自己同型」の素晴らしさに感動しました。今日は，その感動を文章として残すべく（そして，自分の理解度を試すべく）記事をかきたいと思います。

「ガロア理論」や「イデアル論」を前提とした議論が続くので，これまでの記事と比べてレベルはぐーんと跳ね上がると思います。そのため，ある程度勉強したことがある人向けの記事となってしまいますが，ご了承ください。

でも，理解できたら面白い話だと思います！
（そのうち，ここで話した内容の前提となる知識について，もう少し易しくまとめたいですね。）


\newcommand{\Pee}{\mathfrak{P}} \newcommand{\pee}{\mathfrak{p}}

今日の目標

フェルマーの二平方定理（せきゅーんさんによると「フェルマーのクリスマス定理」）から話をはじめましょう。フェルマーの二平方定理とは，以下の定理です。

分解法則１：フェルマーの二平方定理
p \neq 2 なる素数のとき，次が成り立つ：
p \equiv 1 \pmod{4} \;\; \Longleftrightarrow \;\; (p) = (a+b\sqrt{-1})(a-b\sqrt{-1}) \tag{1}

ただし， (a+b\sqrt{-1}), (a-b\sqrt{-1}) は \mathbb{Z}\left[\sqrt{-1}\right] の相異なる素イデアル。

例：
(17) = (4 + \sqrt{-1})(4 - \sqrt{-1})
(29) = (5 + 2\sqrt{-1})(5 - 2\sqrt{-1})


この法則は要するに，ある条件を満たす \mathbb{Q} の整数環 \mathbb{Z} の素イデアル (p) が， \mathbb{Q}(\sqrt{-1}) の整数環 \mathbb{Z}\left[\sqrt{-1}\right] においては素イデアルでなくなってしまう，という素イデアルの分解法則を表しています。


理解を深めるために，もう１つ例を扱います。先ほどは \mathbb{Q}(\sqrt{-1}) を扱いましたが \mathbb{Q}(\zeta_5) においては，以下の法則が成り立ちます。

分解法則２：
p \neq 5 なる素数のとき，次が成り立つ：
p \equiv 1 \pmod{5} \;\; \Longleftrightarrow \;\; (p) = \mathfrak{p}_1 \mathfrak{p}_2 \mathfrak{p}_3 \mathfrak{p}_4 \tag{2}
ただし， \mathfrak{p}_1, \mathfrak{p}_2, \mathfrak{p}_3, \mathfrak{p}_4 は \mathbb{Z}\left[\zeta_5\right] の相異なる素イデアル。

例：
(11) = (2 + \zeta_5)(2 + \zeta_5^2)(2 + \zeta_5^3)(2 + \zeta_5^4)
(31) = (2 - \zeta_5)(2 - \zeta_5^2)(2 - \zeta_5^3)(2 - \zeta_5^4)


こちらの法則も，ある条件を満たす \mathbb{Q} の整数環 \mathbb{Z} の素イデアル (p) が， \mathbb{Q}(\zeta_5) の整数環 \mathbb{Z}\left[\zeta_5\right] においては素イデアルでなくなってしまう，というやはり素イデアルの分解法則を表しています。


これらに共通するのは「代数体を拡大すると，元の体で素イデアルだったものが上の体では分解してしまう」という現象です。「果たしてその分解はいつ起こるのか？」という疑問に答えるのが左辺の条件です。
面白いのは，条件が p \equiv k \mod{m} の形になっているということです。これがなぜなのかを理解したい。


今日の目標は，これらの法則をヒルベルトの理論や円分体の理論を通して理解することです。

大枠だけ述べると，ヒルベルトの理論と円分体の理論の２段構えで説明されます。ヒルベルトの理論は，分解法則はガロア群によってわかる，というものです。円分体の理論では，そのガロア群は (\mathbb{Z}/m\mathbb{Z})^\times に同型だということを教えてくれます。 (\mathbb{Z}/m\mathbb{Z})^\times とは \mod m の世界ですから，なるほど分解法則はたしかに \mod m で説明できるよね，というのが結論です。


最初は何を言っているかわからないかもしれませんが，読んでいけばだんだんわかってくるはずです。

今回の話では，まとめとして以下の図がでてきます。


素イデアル分解の一意性

一般の環においては，素因数分解の一意性は一般には成り立ちません。たとえば， \mathbb{Q}(\sqrt{-5}) においては， 6 という数は以下のように２通りに素因数分解されてしまいます。

6 = 2\cdot 3 = (1+\sqrt{-5})(1-\sqrt{-5})

一方，デデキント環 A においては， A の任意の 0 でないイデアル \mathfrak{a} に対して，以下が成り立ちます。

定理：素イデアル分解の一意性
\mathfrak{a} = \mathfrak{p}_1^{e_1}\mathfrak{p}_2^{e_2}\cdots \mathfrak{p}_g^{e_g} \tag{3}

\mathfrak{p}_1, \mathfrak{p}_2, \cdots, \mathfrak{p}_g は A の相異なる素イデアル

デデキント環においては，素イデアル分解の一意性が保証される。これこそが代数体でイデアルを考える素朴なモチベーションです。「数」より基本的な対象である「イデアル」を考えた方がよいということです。

デデキント環とわざわざ条件がついていますが，一般の代数体（ \mathbb{Q} 上の有限次拡大体）の整数環はデデキント環で，今回は代数体しか扱わないので，デデキント環かどうか確認する必要はありません。

余談ですが，この素イデアル分解の式は，東ドイツで発行された記念切手のデザインに使われました。Wikipediaのこのページ でもみることができます。こんなマニアックな式が切手に採用されたのは後にも先にもこれが最後でしょう。とてもおしゃれなデザインで私は大好きです。この切手が欲しくて欲しくてたまらないのですが，どなたか手に入れる方法を知っている人はいませんか？


以降では「 K の整数環 \mathcal{O}_K の 0 でない素イデアル」のことを単に「 K の素イデアル」ということにします。これは常套句みたいなもので，この手の教科書のどこかに必ずこの一文があります。いちいち「 K の整数環 \mathcal{O}_K の 0 でない素イデアル」なんて言っていたらまどろっこしいですからね。

分岐・不分岐・完全分解

ここから，我々は２つの体の間でおきる分解法則を考えます。一般化のためにそれらを記号で表記しましょう。下の体を K，上の体を L とおき， L/K という代数拡大を考えます。 K, L のいずれも代数体，すなわち \mathbb{Q} の有限次拡大体です。また， K の整数環を \mathcal{O}_K， L の整数環を \mathcal{O}_L と表記します。

最初の具体例で言うと，以下の表のように対応させるといいでしょう。

記号意味分解法則１分解法則２
K代数体（下） \mathbb{Q} \mathbb{Q}
\mathcal{O}_K K の整数環 \mathbb{Z} \mathbb{Z}
L代数体（上） \mathbb{Q}(\sqrt{-1}) \mathbb{Q}(\zeta_5)
\mathcal{O}_L L の整数環 \mathbb{Z}\left[\sqrt{-1}\right] \mathbb{Z}\left[\zeta_5\right]

なぜこんなことをくどくど書くかというと，私が勉強中に混乱したからです。


さてこのとき， K の素イデアル \mathfrak{p} が上の体 L でどのように分解されるかを考えます。その前に，まず \mathfrak{p} が \mathcal{O}_L でイデアルになっていなければなりません。このままだと \mathcal{O}_L のイデアルではないので， \mathfrak{p}\mathcal{O}_L とします。これで， \mathfrak{p} を L の世界に持ち上げることができました。

\mathfrak{p}\mathcal{O}_L の分解は，素イデアル分解の一意性より，以下のように表せます。

\mathfrak{p}\mathcal{O}_L = \mathfrak{P}_1^{e_1}\mathfrak{P}_2^{e_2} \cdots \mathfrak{P}_g^{e_g} \tag{4}

いかつい記号をしていますが， \mathfrak{P}_1, \mathfrak{P}_2, \cdots, \mathfrak{P}_g は L の素イデアルです。 g を \pee の分解指数と呼びます。

ヒルベルトの理論では，ドイツ文字（フラクトゥーア）を頻繁に用いるので，ドイツ文字に慣れていない人はびっくりしてしまいますね。 \mathfrak{P} は大文字の P（ペー） をドイツ文字（フラクトゥーア）で表しています。ちなみに， \mathfrak{p} は小文字の p（ペー） のドイツ文字です。習慣的に，下の体 K の素イデアルを \mathfrak{p} で，上の体 L の素イデアルを \mathfrak{P} で表記します。これは覚えておくとよいかと思います。


ここで， \mathfrak{P}_i \mid \mathfrak{p} です。また，

\mathfrak{P}_i \cap \mathcal{O}_K = \mathfrak{p} \tag{5}

であることに注意しましょう。


いくつか重要な用語を定義しましょう。

まず， e_i を \mathfrak{P}_i の L/K における分岐指数と呼びます。 e_i = 1 のとき， \mathfrak{P}_i は L/K で不分岐といいます。

次に，相対次数を定義するために，こんなものを考えます。

\kappa_{\mathfrak{p}} := \mathcal{O}_K/\mathfrak{p}

環 \mathcal{O}_K をその素イデアル \mathfrak{p} で割っているので \kappa_{\mathfrak{p}} は体になります。元の数は有限なので有限体です。

\kappa_{\mathfrak{P}_i} := \mathcal{O}_L/\mathfrak{P}_i

こちらも有限体です。

さらに， \kappa_{\mathfrak{p}} \subset \kappa_{\mathfrak{P}_i} は有限次拡大体となっています。この拡大次数 [\kappa_{ \mathfrak{P}_i}\colon\kappa_{\mathfrak{p}}] を， \mathfrak{P}_i の L/K における相対次数と呼び， f_i で表します。

f_i = [\kappa_{ \mathfrak{P}_i}\colon\kappa_{\mathfrak{p}}] \tag{6}


すると，以下の等式が成り立ちます。

\displaystyle [L\colon K] = n = \sum_{i=1}^{g} e_i f_i \tag{7}


ここまで説明すると，分岐・不分岐・完全分解・惰性という重要な用語が定義できます。

e_1, e_2, \cdots e_g のいずれか１つでも 1 より大きいとき， \pee は L で分岐する，といいます。

また，すべての e_1, e_2, \cdots, e_g が 1 であるとき， \pee は L で不分岐である，といいます。

今回は簡単のため不分岐のケースを中心に考えることになります。

不分岐で，かつ，すべての相対次数 f_1, f_2, \cdots, f_g が 1 であるとき， \pee は L で完全分解する，といいます。このとき，式 (7) により， g = [L\colon K] となりますから， \pee は L で拡大次数いっぱいの素イデアルに分解することになります。

逆に，不分岐かつ相対次数が [L\colon K] に一致している状況，すなわち，分解せず 1 つの素イデアルのままであるとき， \pee は L で惰性する，といいます。

これらの用語は以下で頻繁に使いますので，覚えておいてください。


これも例をまとめておきましょう。

分解法則１について：

素数の分類分解の状況例
p = 2 \pee は \mathbb{Q}(\sqrt{-1}) で分岐する (2) = (1+\sqrt{-1})^2
p \equiv 1 \pmod 4 \pee は \mathbb{Q}(\sqrt{-1}) で完全分解する (13) = (3+2\sqrt{-1})(3-2\sqrt{-1})
p \equiv 3 \pmod 4 \pee は \mathbb{Q}(\sqrt{-1}) で惰性する (7) は \mathbb{Q}(\sqrt{-1}) の素イデアル

分解法則２について：

素数の分類分解の状況例
p = 5 \pee は \mathbb{Q}(\zeta_5) で分岐する (5) = (1-\zeta_5)^4
p \equiv 1 \pmod 5 \pee は \mathbb{Q}(\zeta_5) で完全分解する (11) = (2 + \zeta_5)(2 + \zeta_5^2)(2 + \zeta_5^3)(2 + \zeta_5^4)
p \equiv 4 \pmod 5 \pee は \mathbb{Q}(\zeta_5) で２つの相異なる素イデアルの積に分解する \begin{eqnarray*} (19) &=& (8 + 3\zeta_5-3\zeta_5^2-3\zeta_5^3+3\zeta_5^4) \\ &\times& (8 - 3\zeta_5+3\zeta_5^2+3\zeta_5^3-3\zeta_5^4) \end{eqnarray*}
p \equiv 2, 3 \pmod 5 \pee は \mathbb{Q}(\zeta_5) で惰性する (17) は \mathbb{Q}(\zeta_5) の素イデアル

ガロア拡大の場合

我々が知りたいことは，上で述べたような分解がどのような法則によって起こるか，ということです。これから紹介するヒルベルトの理論では，分解法則はガロア群によってわかる，ということを教えてくれます。そう，あの「ガロア理論」が武器となるのです。

私は最初にこの話を聞いたとき「素イデアルの分解法則とガロア理論にいったいどんな関係があるのか」と驚きました。でも，とても理にかなった話なのです。実に気持ちのいい理論です。

以降では， L/K をガロア拡大とします。すると，ガロア群が定義できて，

G := \text{Gal}(L/K) \tag{8}

と書くことができます。このガロア群をより深く理解することが，ヒルベルトの理論の目指すところです。

まずは，基本となる体の拡大と群の分解の塔を書きましょう。この図をベースに，これからより詳細な情報が加わっていきます。

分解群

さて，ガロア拡大においては，以下の素イデアルの分解はより簡明になります。

\mathfrak{p}\mathcal{O}_L = \mathfrak{P}_1^{e_1}\mathfrak{P}_2^{e_2} \cdots \mathfrak{P}_g^{e_g} \tag{4}

まず， \sigma \in G を１つ取ってきて， \mathfrak{P}_i へと作用させると \sigma(\mathfrak{P}_i) = \mathfrak{P}_j となり， \mathfrak{p} を割り切る共役な素イデアルへと移ります。 i\neq j とは限りません。

特定の \mathfrak{P} に対して \sigma \in G のすべての元を作用させると， \mathfrak{p}\mathcal{O}_L を割るすべての \mathfrak{P}_i （すなわち， \mathfrak{P} に共役なすべての素イデアル）に移り変わることが示せます。このような状況を「 G は \mathfrak{P}_i 上に推移的に作用する」と言います。

\left\{\sigma(\mathfrak{P}) \;\middle|\; \sigma \in G \right\} = \left\{ \mathfrak{P}_1, \mathfrak{P}_2, \cdots, \mathfrak{P}_g \right\}

ここで， \sigma \in G の中でも特に \sigma(\mathfrak{P}) = \mathfrak{P} となるものだけ集めてくると，これらは G の部分群をなします。これを Z_{\mathfrak{P}} とおいて， L/K における \mathfrak{P} の分解群と呼びましょう。

定義：分解群
Z_{\mathfrak{P}} := \left\{ \sigma \in G \;\middle| \; \sigma(\mathfrak{P}) = \mathfrak{P} \right\} \tag{9}

この Z_{\mathfrak{P}} を， L/K における \mathfrak{P} の分解群と呼ぶ.

分解群 Z_{\mathfrak{P}} の元に対しては， \mathfrak{P} は不変です。一方， Z_{\mathfrak{P}} のあとに \sigma \in G を作用させた \sigma Z_{\mathfrak{P}} は， \mathfrak{P} を共役な素イデアルへと推移させます。

したがって，

G/Z_{\Pee} = \{ \sigma_1 Z_{\mathfrak{P}}, \sigma_2 Z_{\mathfrak{P}}, \cdots, \sigma_g Z_{\mathfrak{P}} \}

のそれぞれの元に対して， \Pee は相異なる共役な素イデアル \Pee_1, \Pee_2, \cdots, \Pee_g へと移されることになります。よって，

\#(G/Z_{\Pee}) = g

が成り立ちます。まさに， Z_{\Pee} は素イデアルの分解を司る部分群ということになりますね。


また，式 (4) の両辺に \sigma \in G を作用させると，

\sigma(\mathfrak{p}\mathcal{O}_L) = \sigma(\Pee_1)^{e_1}\sigma(\Pee_2)^{e_2} \cdots \sigma(\Pee_g)^{e_g}

となるわけですが， \pee は K の元なので \sigma(\pee\mathcal{O}_L) = \pee\mathcal{O}_L です。また， \Pee_i は \sigma(\Pee_i) = \Pee_j と異なる元に移されます。このときに，もし e_i \neq e_j であれば，素イデアル分解の一意性に反します。したがって， \pee について，すべての分岐指数は等しくなります。これを e とおくと，

e = e_1 = e_2 = \cdots = e_g

が成り立ちます。

また，ここでは示さないですが，ガロア拡大においては相対次数 f_i もすべて等しくなります。これを f とおくと

f = f_1 = f_2 = \cdots = f_g

です。


以上より，ガロア拡大においては，式 (7) は以下のように非常に簡単になります。

\displaystyle [L\colon K] = n = e f g \tag{7'}

結局， \Pee \mid \pee を１つとってきたときに，

\displaystyle \#(G / Z_\Pee) = g
\displaystyle \#Z_\Pee = ef

が成り立ちます。

体の拡大と群の分解の塔を作ると，次のような図が得られます。

あくまで， \Pee \mid \pee についての図を作っていることに注意してください。固定している \pee, \; \Pee が変わると，この図も変わってしまいます。

惰性群

まだまだ続きます。分解群 Z_\Pee を使って，有限体 \kappa_\Pee / \kappa_\pee の拡大を理解します。

\kappa_\Pee = \mathcal{O}_L/\Pee の元は， x + \Pee と表せます。ここで x \in \mathcal{O}_L です。この元に分解群 Z_\Pee の元 \sigma を作用させると，

x + \Pee \mapsto \sigma(x+ \Pee) = \sigma(x) + \Pee

となります。すなわち， \kappa_\Pee から \kappa_\Pee への自己同型写像になっています。

また， \sigma は \mathcal{O}_K の元を固定するので， \kappa_{\pee} = \mathcal{O}_K/\pee の元も固定します。このことは，すなわち \sigma は \kappa_\Pee / \kappa_\pee の自己同型写像 \overline{\sigma} を誘導することを意味します。

具体的には，

という対応を考えることになります。

この \pi は全射であることが示せます。また，単射ではありません。 \#Z_\Pee = ef と \#\text{Gal}(\kappa_\Pee / \kappa_\pee) = f が合っていないからです。実際， \overline{\sigma} \in Z_\Pee に対し

\sigma'(x) \equiv \overline{\sigma}(x) \pmod{\Pee}

を満たすような \sigma' は \mod{\Pee} において複数存在します。この重複を潰すために，惰性群とよばれる Z_\Pee の部分群を定義します。

定義：惰性群
T_{\mathfrak{P}} := \left\{ \sigma \in Z_\Pee \;\middle| \; \alpha \in \mathcal{O}_L, \; \sigma(\alpha) \equiv \alpha \pmod\Pee \right\} \tag{10}

この T_\Pee を L/K における \Pee の惰性群と呼びます。

T_\Pee は定義より，

T_\Pee = \text{ker}(\pi)

です。この惰性群によって分解群を潰してあげると，

\overline{\pi} \colon Z_\Pee/T_\Pee \longrightarrow \text{Gal}(\kappa_\Pee / \kappa_\pee)

という対応により，両者は同型になります。

\# Z_\Pee = ef かつ \# (Z_\Pee/T_\Pee) = f なので， \# T_\Pee = e となります。




図で表しましょう。


さぁ，これで代数体のガロア群と有限体のガロア群が結びつきました！

e = 1 のとき，すなわち \pee が不分岐のときですが，このときは惰性群 T_\Pee がつぶれるので，分解群 Z_\Pee が有限体のガロア群と完全に一致します。

以上のことから， \pee の分解法則が有限体を通してわかります。ようやく本題に戻ってきた感じがしますね！笑

[ L\colon K] = efg より， e = 1 のときは，

g = [ L\colon K] \big/ f

が成り立ちます。

f = 1 すなわち \text{Gal}(\kappa_\Pee / \kappa_\pee) が単位群に潰れているときは， g = [ L\colon K] となり \pee は完全分解します。

有限体の拡大次数 f によって，分解法則がわかるのです。

有限体とフロベニウス自己同型

以上の議論により，ようやくこの有限体の拡大を調べたいというモチベーションが湧いたわけなのですが，この有限体はいったいどんなやつなんでしょうか。

実は，非常にありがたいことに，有限体の拡大にはわかりやすい法則があります。


有限体のフロベニウス自己同型
E を有限体とし位数を q = \#E とおく．また， F/E を標数 p の有限体の d 次拡大とする．このとき， F の E 上の自己同型群 \text{Gal}(F/E) は位数 d の巡回群である．さらに，

\mathrm{Frob}_{q} \colon F \to F, \; x \mapsto x^{q}

は \text{Gal}(F/E) の生成元である．すなわち，

\text{Gal}(F/E) = \langle \mathrm{Frob}_{q} \rangle

が成り立つ．この自己同型 \mathrm{Frob}_{q} をフロベニウス自己同型という．


なんと，有限体のガロア群は巡回群で，なおかつその生成元は具体的にわかっているというんです。これはやばいですね。「フロベニウスやばい！」と叫んでしまいたくなります。

今回の問題においては，

\text{Gal}(\kappa_\Pee/\kappa_\pee)

を考えているわけですが，

\mathrm{Frob}_{\#\kappa_{\pee}}(x) = x^{\#\kappa_\pee}

で定義される \mathrm{Frob}_{\#\kappa_{\pee}} によって，

\text{Gal}(\kappa_\Pee/\kappa_\pee) = \langle \mathrm{Frob}_{\#\kappa_\pee} \rangle

のように生成できるのだそうです。

ところで， \mathrm{Frob}_{\#\kappa_\pee} が，ちゃんと \kappa_\pee を固定する自己同型になっていることがわかりますか？

\kappa_\pee は有限体なので， 0 を除く元は乗法に対して群をなします。これを \kappa_\pee^{\times} とおきます。群論のフェルマーの小定理より，

x^{\#\kappa_\pee-1} = 1

両辺に x をかけて，

x^{\#\kappa_\pee} = x

が成り立ちます。したがって \kappa_\pee^{\times} の元は \mathrm{Frob}_{\#\kappa_\pee} によって不変です。また， 0 は明らかに不変なので， \mathrm{Frob}_{\#\kappa_\pee} が \kappa_\pee を固定することがわかりました。


話を代数体に戻すと， \overline{\pi} によって Z_\Pee/T_\Pee と \text{Gal}(\kappa_\Pee/\kappa_\pee) = \langle \mathrm{Frob}_{\#\kappa_\pee} \rangle が同型です。したがって， Z_\Pee/T_\Pee も

\overline{\pi}^{-1}(\mathrm{Frob}_{\#\kappa_\pee})

によって生成される巡回群になります。


いやぁ，すごいですね！


群の対応関係のイメージはこのような感じでしょうか。



ここから不分岐に限定した話をします。

不分岐の場合は T_\Pee がつぶれるので， \mathrm{Frob}_{\#\kappa_\pee}に対応する Z_\Pee の元がただ１つ定まります。この元ただ１つによって分解群 Z_\Pee が生成されます。要するに，分解のすべてがわかるのです。

こんな特別な元には名前をつけておきましょう。このようなを L/K における \Pee に関するフロベニウス自己同型と呼び \left[ \frac{L/K}{\;\Pee\;}\right] と表記します。

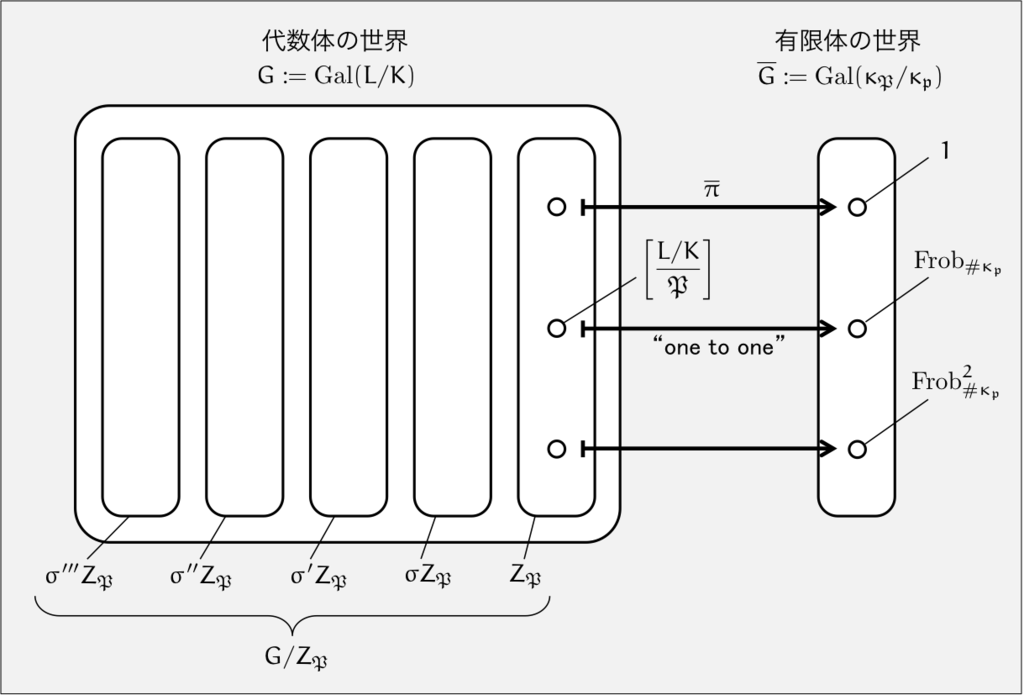
このフロベニウス自己同型 \left[ \frac{L/K}{\;\Pee\;}\right] は有限体 \kappa_\Pee 上に制限すると \mathrm{Frob}_{\#\kappa_\pee} として振舞うので，

\displaystyle \left[ \frac{L/K}{\;\Pee\;}\right](\alpha) \equiv \mathrm{Frob}_{\#\kappa_{\pee}}(\alpha) \pmod \Pee, \;\; \alpha \in \kappa_\Pee \tag{11}

を満たす G の元として定めることができます。


この \left[ \frac{L/K}{\;\Pee\;}\right] により，不分岐の場合は Z_\Pee は以下のように生成されます。

\displaystyle Z_\Pee = \left\langle \left[ \frac{L/K}{\;\Pee\;}\right] \right\rangle \tag{12}

フロベニウス自己同型の Z_\Pee 上の位数がわかれば， Z_\Pee の大きさ，すなわち相対次数 f がわかり，分解指数 g もわかります。


これにて最初の問題の１つは解決しました。

ヒルベルトの理論は，分解法則はガロア群によってわかる，というものです。

この意味は， \pee の分解法則が分解群 Z_\Pee によってわかるということと，その Z_\Pee は不分岐の場合，有限体のフロベニウス自己同型というわかりやすい対象によってかけるということです。

もはや，もうだいぶ満足してきたので，このへんで終わりにしていいくらいですが。笑


もう１つの問題は「分解法則がなぜ \mod m でかけるのか」でしたね。これについては，円分体の理論を用いて簡単に説明しましょう。

円分体の理論

これまで L/K は，抽象的な代数体を扱ってきましたが，ここでは今回の目的に合わせて具体的な体を考えます。

まず， K = \mathbb{Q} です。有理数体上の拡大を考えます。さらに， L = \mathbb{Q}(\zeta_m) です。ここで， \zeta_m は１の原始 m 乗根です。

\displaystyle \zeta_m := \exp\left(\frac{2\pi i}{m} \right)

L = \mathbb{Q}(\zeta_m) は円分体と呼ばれており，円分体の理論により \mathbb{Q}(\zeta_m)/\mathbb{Q} のガロア群に対し，以下のような同型が知られています。

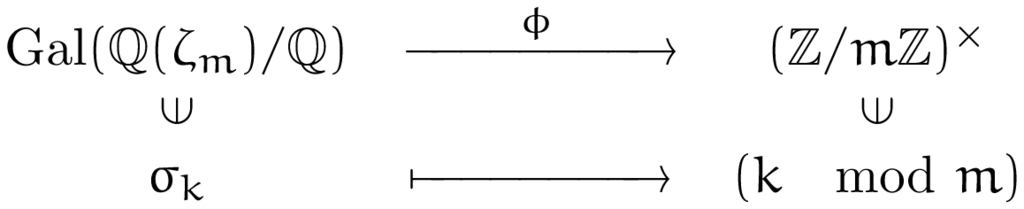
ここで， \sigma_k \in \text{Gal}(\mathbb{Q}(\zeta_m)/\mathbb{Q}) は，

\sigma_k(\zeta_m) = \zeta^k_m

で定義されます。

上記の事実は，円分体のガロア群の情報が \mod m の世界で表現できることを意味しています。我々の目的としては，フロベニウス自己同型の位数を知りたいわけです．その目的は，対応する \mod m を考えることにより達成されます。


具体的に考えるために，フロベニウス自己同型をみつけましょう。 \pee = p\mathbb{Z}, \; \Pee \mid \pee として，有限体 \kappa_\pee = \mathbb{Z}/\pee を考えます。 \#\kappa_\pee = p より，フロベニウス自己同型 \mathrm{Frob}_p は，

\mathrm{Frob}_p(x) = x^p

で与えられます。

\mathbb{Q}(\zeta_m)/ \mathbb{Q} における \Pee に関するフロベニウス自己同型は，

\displaystyle \sigma(\alpha) \equiv \alpha^{p} \pmod \Pee, \;\; \alpha \in \kappa_\Pee

を満たすような \sigma \in G ですが，これは以下の法則で与えられます。

円分体のフロベニウス自己同型
\Pee \mid \pee, \; \pee = p\mathbb{Z} とし， \pee が \mathbb{Q}(\zeta_m)/\mathbb{Q} において不分岐であるとき， \mathbb{Q}(\zeta_m)/\mathbb{Q} における \Pee に関するフロベニウス自己同型 \left[\frac{\mathbb{Q}(\zeta_m)/\mathbb{Q}}{\;\Pee\;}\right] が定義できて，具体的に以下で与えられる．
\displaystyle \left[\frac{\mathbb{Q}(\zeta_m)/\mathbb{Q}}{\;\Pee\;}\right] = \sigma_p

ただし， \sigma_p は \sigma_p \colon \zeta_m \longrightarrow \zeta_m^p であるような \text{Gal}(\mathbb{Q}(\zeta_m)/\mathbb{Q}) の元．

あとは， \sigma_p の G における位数を考えれば良いわけです。つまり， \sigma_p^f = e となる f を見つければよいのです。

一方で， G は (\mathbb{Z}/m\mathbb{Z})^\times に同型であるという事実がありました。その対応は具体的に与えられていて，

\sigma_p \; \mapsto \; \overline{p}

となります。したがって， \sigma_p の位数 f は \overline{p} \in (\mathbb{Z}/m\mathbb{Z})^\times の位数と一致します。結果として，以下の分解法則が成り立ちます。

円分体の素イデアル分解法則
(\mathbb{Z}/m\mathbb{Z})^\times 上の \overline{p} の位数を f としたとき，すなわち
p^f \equiv 1 \pmod m

を満たす最小の f を考えたとき，素数 p は \mathbb{Q}(\zeta_m) において g 個の素イデアルの積に分解される． g は以下で定まる．

g = [\mathbb{Q}(\zeta_m)\colon \mathbb{Q}] \big/ f = \varphi(m) \big/ f \tag{13}


これらの法則については，具体的に計算して確認していきましょう。

最初の問題を解こう

K = \mathbb{Q}, L = \mathbb{Q}(\sqrt{-1}) の場合：

まず， L = \mathbb{Q}(\sqrt{-1}) = \mathbb{Q}(\zeta_4) であることに注意しましょう。これも円分体です。

不分岐のときを考えたいので， p\neq 2 とします。

円分体の相互法則により， \mathbb{Q}(\zeta_4)/ \mathbb{Q} における \Pee に関するフロベニウス自己同型 \left[ \frac{\mathbb{Q}(\zeta_4)/ \mathbb{Q}}{\;\Pee\;}\right] は，以下で与えられる。

\displaystyle \left[ \frac{\mathbb{Q}(\zeta_4)/ \mathbb{Q}}{\;\Pee\;}\right] = \sigma_p

ただし， \sigma_p \colon \zeta_4 \mapsto \zeta_4^p である。この \sigma_p の位数によって，相対次数 f が得られ，分解法則が明らかになる。

p \equiv 1 \pmod 4 のとき：

\sigma_p \colon \zeta_4 \mapsto \zeta_4^p = \zeta_4^1

となり，フロベニウス自己同型は恒等写像である。よって，その位数は 1 であり， f= 1 である。

したがって，

[\mathbb{Q}(\sqrt{-1})\colon \mathbb{Q}] = fg

より，

g = [\mathbb{Q}(\sqrt{-1})\colon \mathbb{Q}] = 2

すなわち， p は \mathbb{Q}(\sqrt{-1}) で完全分解する。

p \equiv 3 \pmod 4 のとき：

\sigma_p \colon \zeta_4 \mapsto \zeta_4^p = \zeta_4^3

となる。

\sigma_p^2(\zeta_4) = \sigma_p(\sigma_p(\zeta_4)) = \zeta_4^9 = \zeta_4^1

より， \sigma_p の位数は 2 であり， f= 2 である。

したがって，

[\mathbb{Q}(\sqrt{-1})\colon \mathbb{Q}] = fg

より，

g = [\mathbb{Q}(\sqrt{-1})\colon \mathbb{Q}] \big/ 2 = 1

すなわち， p は \mathbb{Q}(\sqrt{-1}) で惰性する。

別の見方：

上では，ある条件の p が完全分解するかどうかを見ていましたが，逆に完全分解する p の条件を見つけることはできないでしょうか。これまで述べたように， p が完全分解するのは，フロベニウス自己同型が恒等写像になるときでした。

以下の同型，

により， \sigma_p が恒等写像ということは p が \mod{m} で 1 に合同ということです。よって， p \equiv 1 \pmod m のとき， p は完全分解するということになりますね。

K = \mathbb{Q}, L = \mathbb{Q}(\zeta_5) の場合：

ほぼ同様に進める。

不分岐のときを考えたいので， p\neq 5 とします。

円分体の相互法則により， \mathbb{Q}(\zeta_5)/ \mathbb{Q} における \Pee に関するフロベニウス自己同型 \left[ \frac{\mathbb{Q}(\zeta_5)/ \mathbb{Q}}{\;\Pee\;}\right] は以下で与えられる．

\displaystyle \left[ \frac{\mathbb{Q}(\zeta_5)/ \mathbb{Q}}{\;\Pee\;}\right] = \sigma_p

ただし， \sigma_p \colon \zeta_5 \mapsto \zeta_5^pである。この \sigma_p の位数によって，相対次数 f が得られ，分解法則が明らかになる。

p \equiv 1 \pmod 5 のとき：

\sigma_p \colon \zeta_5 \mapsto \zeta_5^p = \zeta_5^1

となり，フロベニウス自己同型は恒等写像である。よって，その位数は 1 であり， f= 1 である。

したがって，

[\mathbb{Q}(\zeta_5)\colon \mathbb{Q}] = fg

より，

g = [\mathbb{Q}(\zeta_5)\colon \mathbb{Q}] = 4

すなわち， p は \mathbb{Q}(\zeta_5) で完全分解する。

p \equiv 4 \pmod 5 のとき：

\sigma_p \colon \zeta_5 \mapsto \zeta_5^p = \zeta_5^4

となる。

\sigma_p^2(\zeta_5) = \sigma_p(\sigma_p(\zeta_5)) = \zeta_5^{16} = \zeta_5^1

より， \sigma_p の位数は 2 であり， f = 2 である。
（「 (\mathbb{Z}/5\mathbb{Z})^{\times} において 4 の位数が 2 である。ゆえに f= 2 」としてもよい。）

したがって，

[\mathbb{Q}(\zeta_5)\colon \mathbb{Q}] = fg

より，

g = [\mathbb{Q}(\zeta_5)\colon \mathbb{Q}] \big/ 2 = 2

すなわち， p は \mathbb{Q}(\zeta_5) で２つの相異なる素イデアルの積に分解する。


p \equiv 2 \pmod 5 のとき：

\sigma_p \colon \zeta_5 \mapsto \zeta_5^p = \zeta_5^2

となる。

\sigma_p^2(\zeta_5) = \sigma_p(\sigma_p(\zeta_5)) = \zeta_5^{4}

よって，

\sigma_p^4(\zeta_5) = \zeta_5^{1}

より， \sigma_p の位数は 4 であり， f = 4 である。
（「 (\mathbb{Z}/5\mathbb{Z})^{\times} において 2 の位数が 4 である。ゆえに f= 4 」としてもよい。）


したがって，

[\mathbb{Q}(\zeta_5)\colon \mathbb{Q}] = fg

より，

g = [\mathbb{Q}(\zeta_5)\colon \mathbb{Q}] \big/ 4 = 1

すなわち， p は \mathbb{Q}(\zeta_5) で惰性する。


p \equiv 3 \pmod 5 のとき：

\sigma_p \colon \zeta_5 \mapsto \zeta_5^p = \zeta_5^3

となる。

\sigma_p^2(\zeta_5) = \sigma_p(\sigma_p(\zeta_5)) = \zeta_5^{4}

よって，

\sigma_p^4(\zeta_5) = \zeta_5^{1}

より， \sigma_p の位数は 4 であり， f = 4 である。
（「 (\mathbb{Z}/5\mathbb{Z})^{\times} において 2 の位数が 4 である。ゆえに f= 4 」としてもよい。）


したがって，

[\mathbb{Q}(\zeta_5)\colon \mathbb{Q}] = fg

より，

g = [\mathbb{Q}(\zeta_5)\colon \mathbb{Q}] \big/ 4 = 1

すなわち， p は \mathbb{Q}(\zeta_5) で惰性する。

まとめ

この図に尽きます。

代数体の分解をつかさどる「分解群」が，有限体の拡大についてのガロア群と同型になって結びつくというのがポイントでした。さらにそのガロア群は「フロベニウス自己同型」というわかりやすい自己同型写像によって生成されるわけですね。

「フロベニウス自己同型すごい！」

と叫びたくなります。あとは，フロベニウス自己同型の位数を調べることで，素数の分解法則がよくわかる，ということでした。

最後の位数を調べるときには，代数体の具体的な性質（円分体のガロア群は，既約剰余類群 (\mathbb{Z}/m\mathbb{Z})^\times に同型）を使いました。こうやって考えると円分体ってとても扱いやすいんですね。

参考文献

まだまだ全然理解できていないのですが，ひとまず以下の本をとっかえひっかえ見ながら，ちょっとずつ勉強しています。ようやく最近，相互の文献における記号の対応関係がわかってきました。

代数的整数論 第2版

代数的整数論 第2版

Amazon

数論序説

数論序説

Amazon

数論I: Fermatの夢と類体論

数論I: Fermatの夢と類体論

Amazon


尾崎学先生の「ガロアからの見た現代数学」という連載が大変参考になりました。この記事のおかげで，分解群のイメージが得ることができました。

現代数学 2015年 09 月号 [雑誌]

現代数学 2015年 09 月号 [雑誌]

  • 現代数学社
Amazon

*1:正直なところ，不勉強ゆえに「類体論」や「ヒルベルトの理論」が差す範囲をよくわかっていなかったりします。間違ったことを言っていればご指摘ください。