一時期話題になった素数のスモールギャップに関するプレプリントについて

この記事は明日話したくなる数学豆知識アドベントカレンダーの 3日目の記事です。（2 日目：統計学における自由度）

一時期、こんなニュースが飛び交って話題になったことを覚えていますでしょうか。

http://www.47news.jp/CN/201402/CN2014022601001180.html
http://www.sponichi.co.jp/society/news/2014/02/26/kiji/K20140226007668140.html

ジェームズ・メイナード博士とテレンス・タオ博士という２人の博士によって、素数についての興味深い定理が発見されて、それが『教科書を書き換える』ほどの大発見だそうです。
いったいどんな定理なのか気になりますね。

この記事では、「その定理が意味するところは何なのか？」「何がすごいのか？」解説したいと思います。

かなり長いので気を付けてください。笑

まずはニュースの中身を読んでみよう

ところで、このニュースに書いてある定理の意味するところについてですが、何を書いてあるのかわかりますか？
以下のように一部引用します。少し時間をあげますので読んでみてください。

数が大きくなると、素数はまばらにしか見つからない。１～１００の１００個の中には２、３、５など素数は２５個あるが、同じ１００個でも、１０万１～１０万１００には素数は６個しかない。では数が大きくなると、素数の間隔は際限なく離れていくのか。新定理は「そんなことはない」と否定する結果を示した。
（中略）
例えば、ある素数と次に大きい素数の２個を考える。１９なら次は２３で、１９～２３の５個の中に２個の素数がある。だが数が大きくなっても、５個の自然数が並んだ中に素数が２個あるかは分からない。
　新定理では、どんな大きな数でも、６００個ごとに区切ると素数が２個含まれる場合があると分かった。必ず２個あるわけではないが、２個の素数が含まれる６００個ごとの区間は無限に存在する。今後の研究で、区間の幅はもっと狭まる可能性があるが、現時点では６００が最小の幅という。
　次のようなイメージだ。ある大きな数ｎを例に考える。ｎ、ｎ＋１、ｎ＋２…、ｎ＋１０００…、ｎ＋２０００…と順番に大きくなる数字を書いた札を作り、６００個ずつ同じ箱に入れる。すると、全ての箱に２個の素数が入るとは限らないが、素数２個が入った箱は無限にあることになる。

47NEWS（よんななニュース）
「素数の間隔で新定理発見　極端な偏りなく分布、米英数学者」より一部引用

・・・

ありがとうございます。

読んでもらって悪いですが、私にはなんのことやらわかりません。笑
まず、文章の意味が分からないのです。素数の分布が関係してること、６００という数字が関係していること、あたりはなんとかわかります。

ニュースを見ていても埒があきませんから、原文をみて、もとの意味するところを考えていきたいと思います。
ただし、原文をそのまま読んでもわからないかと思うので、前提となる知識を軽く紹介しておいてから、ポイントをかいつまんで説明しましょう。

この問題は、《双子素数予想》という古くからある未解決問題を解くための、途中過程と考えるとわかりやすいです。

双子素数予想とは

双子素数予想とは次のような予想のことです。

《双子素数予想》
差が 2 であるような連続する素数の組（双子素数）は無限に存在する

素数は、その数と 1 以外でしか割り切ることができない数のことですね。
列挙していくと、

2, 3, 5, 7, 11, 13, 17, 19, ...

と無限に続いています。

ここで双子素数とは、

(3, 5), (5, 7), (11, 13), (17, 19), ...

というように、差が2であるような連続する素数の組のことです。これが無限に存在することを主張するのが双子素数予想です。

「予想」とついているわけですから、まだ証明されているわけではありません。
最初のほうには、結構な頻度で双子素数が登場しますから、このままずっと存在するような気もします。

ところが、素数の頻度は、数が大きくなればなるほど下がってきます。それに合わせて双子素数の頻度も下がっていきます。したがって、双子素数が無限に存在することは自明ではありません。

メイナード博士らの結果

さて、最初の問題がどのように双子素数予想に結びつくのでしょう。ニュースによると、今回の結果はジェームズ・メイナード博士とテレンス・タオ博士が独立に発見したそうです。博士の発表した原文を見てみましょう。

ジェームズ・メイナード博士の書いた原文はこちら（リンク先右上の「PDF」をクリック）
[1311.4600v2] Small gaps between primes

論文のPDFはarXivというサイトに上がっています。正確にいうと、この段階ではまだ論文ではないのですが（これについては後で述べます）。

ジェームズ・メイナード博士が解いた定理（の中でニュースで触れられている定理）に相当するものは、原文2ページの下のほうにある Theorem 1.3. にあたるものです。（「Theorem」は英語で「定理」のことです。）

Theorem 1.3.
$\displaystyle \liminf_{n \to \infty}(p_{n+1}-p_{n}) \leq 600$

さて、 $p_n, p_{n+1}$ は連続する $n$ 番目, $n+1$ 番目の素数を表します。
右辺の $600$ はニュースにも登場した数値ですね。
ここで、lim inf という記号が何を意味するのかが分かれば、定理の意味はつかめそうです。これが非常に曲者でわかりにくいのですが・・・。以下で、丁寧に追っていきましょう。

lim inf とは

lim inf は「下極限」を表す記号です。limとinfを組み合わせた複合的な記号になっています。Wikipedia にも定義は書いてありますが、これがどうにもわかりづらい。素数の話は一旦置いておいて、この記号の意味するところを理解することから始めましょう。
（このセクションの説明が一番長いので、分かる方は次のセクションまで飛ばしてもらってかまいません。）

上極限と下極限 - Wikipedia

lim inf は次の式で定義されます。

$\displaystyle \liminf_{n \to \infty} a_n = \lim_{n \to \infty} \left(\inf_{k>n} a_k\right)$

ここで、 $a_n$ は数列です。lim と inf の組み合わせで表現されていますね。最終的に得られる値は数列ではなく数値になります。後ろに来る数列に対して、何らかの方法で極限を取った値が得られる訳です。

分かりづらいので一個ずついきましょう。まずは $b_n$ という数列を以下のように定義しておきましょう。元の式の右辺の一部分ですね。

$\displaystyle b_n = \inf_{k>n} a_k$

さて、ここで inf という謎の記号が登場します。この記号は「下限」を表す記号で、英語では「inferior」です。（読み方はたぶん「インフェリア」とそのまま読むのがいいかと思いますが、よくわかりません。）

inf はその後ろにくる数列の「下限」をとります。この「下限」をとる数列の範囲を inf の下に不等式で書いています。この場合だと、ある特定の $n$ に対して $k>n$ を満たすような範囲で $a_k$ を考えて、その「下限」を取るのです。

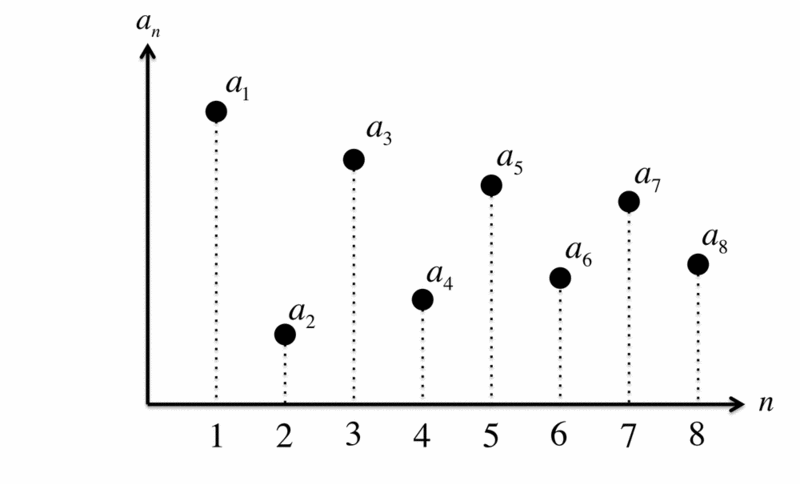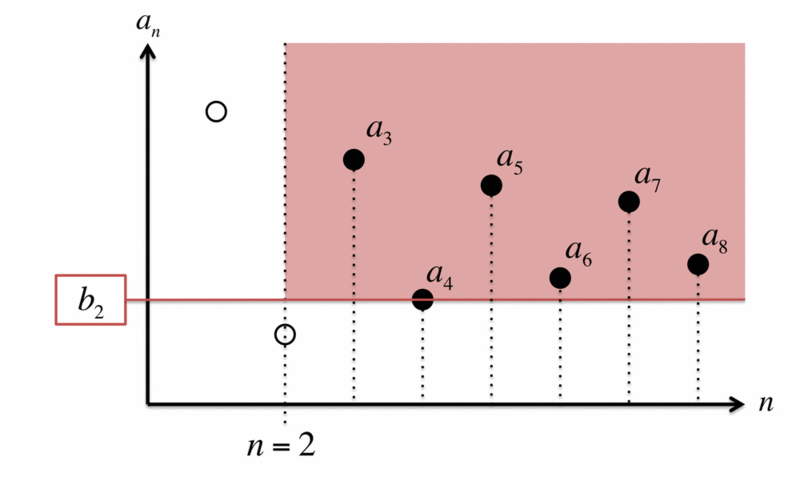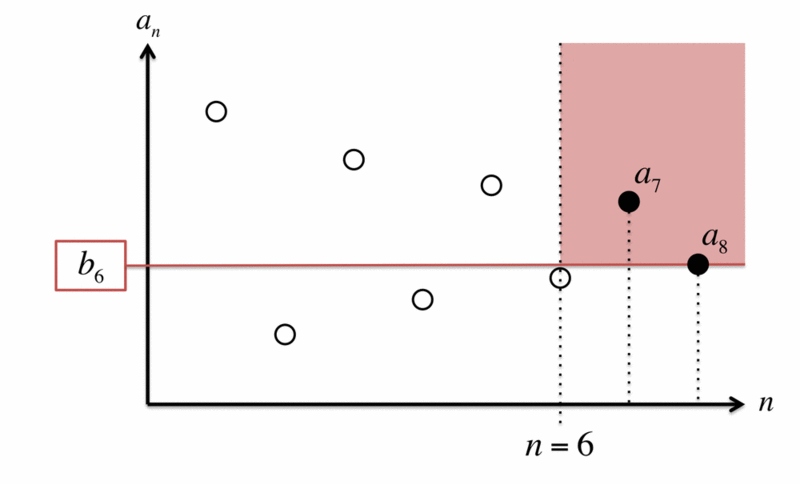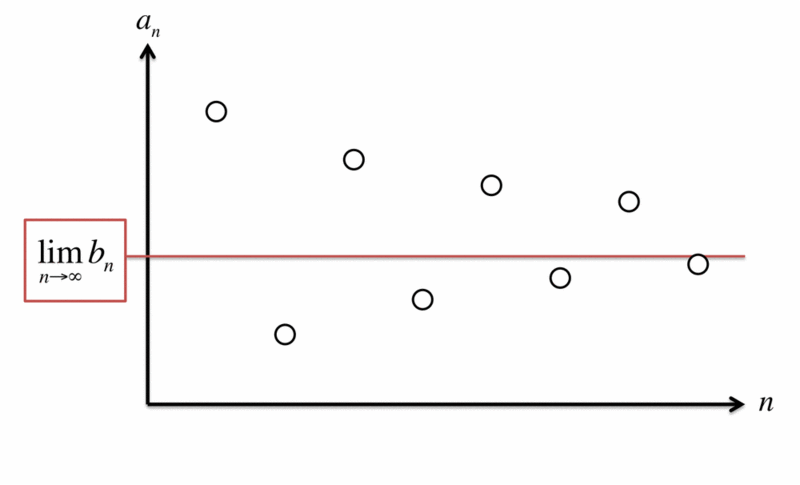
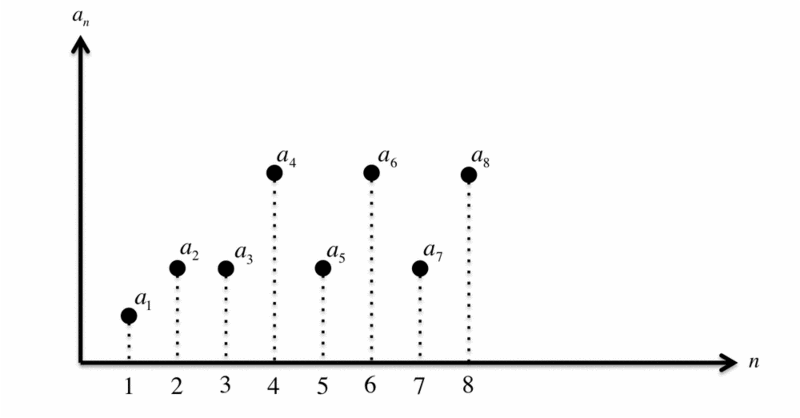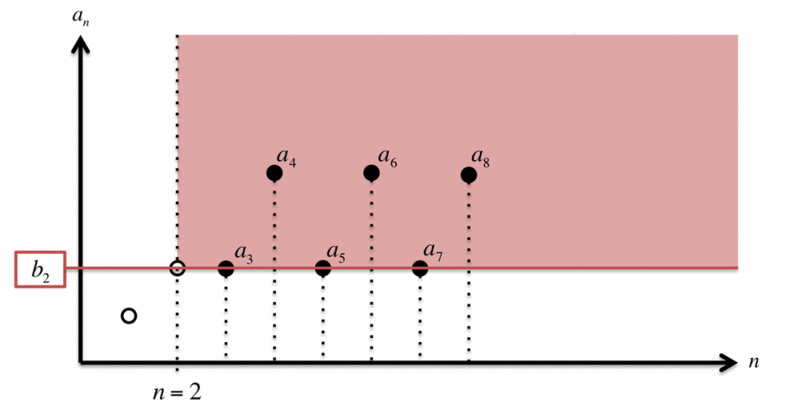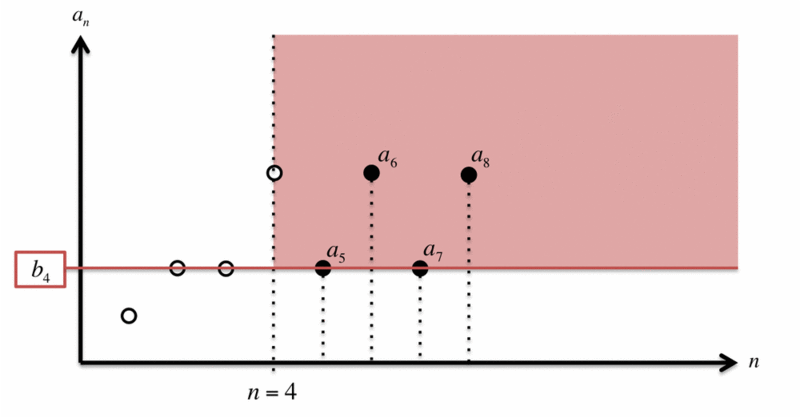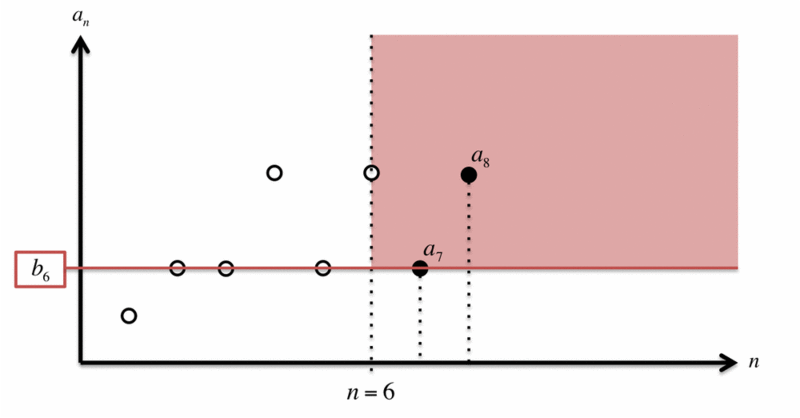
具体例を示しましょう。数列 $a_n$ を考えて、次のようにグラフに示します。横軸を $n$ , 縦軸を $a_n$ とします。

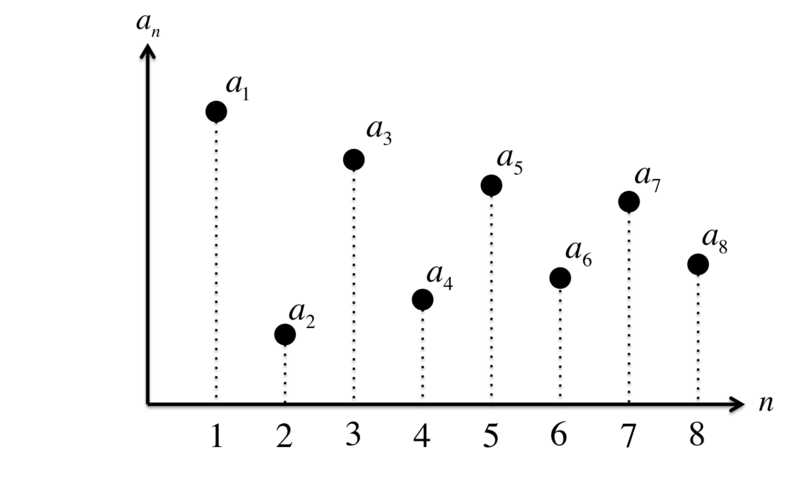
f:id:tsujimotter:20141202230841p:plain:w400

ここで、 $n=1$ のときの「下限」 $\displaystyle b_1=\inf_{k>1} a_k$ を考えます。これは、緑色に示すような $k > 1$ の領域の $a_k$ を考えて、その領域内の $a_k$ の「下限」である $b_1$ （赤線）を求めれば良いわけです。
f:id:tsujimotter:20141202234653p:plain:w270 f:id:tsujimotter:20141202234709p:plain:w270
$k>1$ のすべての $a_k$ が「下限」 $b_1$ より上、すなわち、赤色の領域に含まれていることを確認してください。

同様に $n=2$ のときは、次の図のように $b_2$ が決まります。

f:id:tsujimotter:20141202231129p:plain:w400

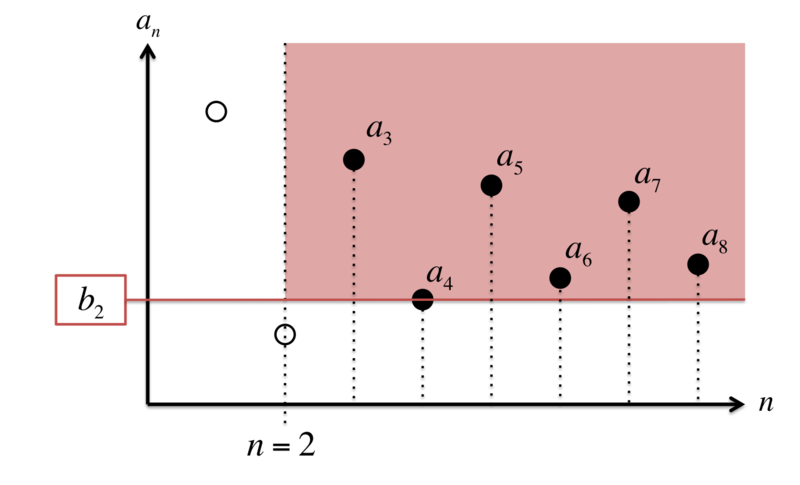
今回の記事の内容に限っては、「下限」は「最小値」と同じものだと思ってもらってかまいません。

ただし、一般には数列が最小値を持たない場合があります。たとえば、 $a_n = 1/n$ の場合は、 $n > 0$ で限りなく $0$ に近づくような数列になっていますが、 $a_n$ がちょうどぴったり $0$ にならないですよね。この場合でも「下限」は $0$ なのです。

また、発散して最小値が存在しない場合もあります。その場合も「下限」なら $\displaystyle \inf_{k>n}{a_k}=-\infty$ のように表現することが出来ます。意味としては「下限なし」といったところでしょう。

さて、inf が分かったので、今度は lim inf を考えましょう。元の式に下限 $b_n$ を代入したものが、次の式です。

$\displaystyle \liminf_{n \to \infty} a_n = \lim_{n \to \infty} \left(\inf_{k>n} a_k\right) = \lim_{n \to \infty} b_n$

先ほどの流れで、 $b_n$ を計算していって、 $n$ の値をどんどん大きくしていくと、一定の値に収束するはずです。
f:id:tsujimotter:20141202231129p:plain:w180 f:id:tsujimotter:20141202233524p:plain:w180 f:id:tsujimotter:20141202233532p:plain:w180

その値が $\displaystyle \lim_{n\to \infty} b_n$ です。

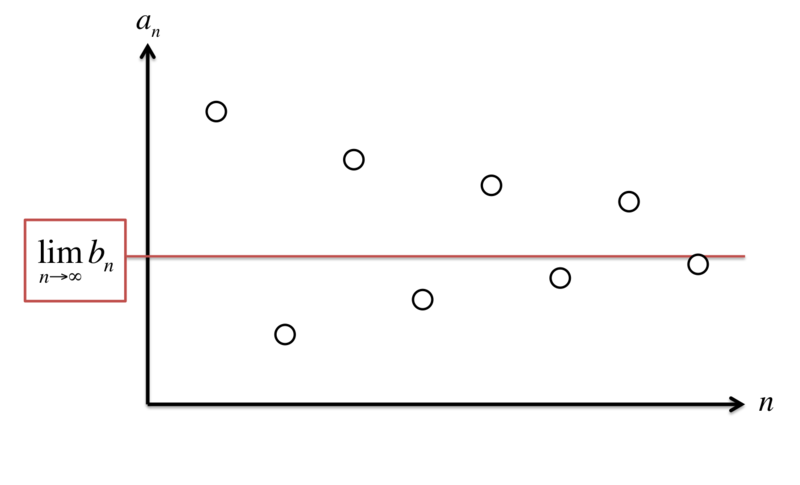
f:id:tsujimotter:20141202233926p:plain:w400

そして、この値こそが $\displaystyle \liminf_{n\to\infty} a_n$ だったのです。

極限に近づいていくさまを、GIFアニメでも表してみました。

f:id:tsujimotter:20141202230728g:plain:w400

数式のイメージはつかめましたでしょうか？

双子素数予想との関連は

lim inf に慣れてもらったところで、素数の話に戻りましょう。元の式の左辺は、lim inf を使って次のように表されるのでした。

$\displaystyle \liminf_{n\to\infty} \left(p_{n+1} - p_n\right)$

ここで、

$a_n = p_{n+1} - p_n$

とおけば、先ほどの $a_n$ と対応づけて同じような図を書くことが出来ますね。

順番に素数を並べ、その差をとっていって、 $a_n$ を計算していきましょう。

$a_1 = p_2 - p_1 = 3 - 2 = 1$
$a_2 = p_3 - p_2 = 5 - 3 = 2$ （双子素数）
$a_3 = p_4 - p_3 = 7 - 5 = 2$ （双子素数）
$a_4 = p_5 - p_4 = 11 - 7 = 4$
$a_5 = p_6 - p_5 = 13 - 11 = 2$ （双子素数）
$a_6 = p_7 - p_6 = 17 - 13 = 4$
$a_7 = p_8 - p_7 = 19 - 17 = 2$ （双子素数）
$a_8 = p_9 - p_8 = 23 - 19 = 4$

すると、こんなグラフになるはずです。

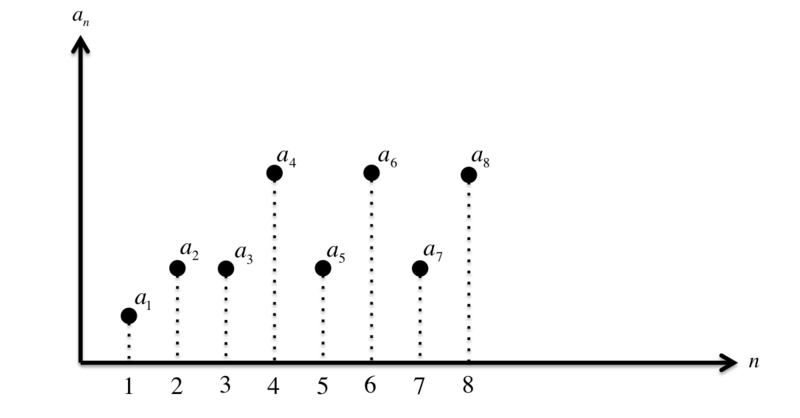
f:id:tsujimotter:20141203005902p:plain:w400

これを使って、順に $\displaystyle b_n = \inf_{k>n} a_k$ を計算していきましょう。先ほど丁寧に説明しましたので、今度は結果だけをGIFアニメで紹介します。

f:id:tsujimotter:20141203005941g:plain:w400

$b_1$ から $b_6$ までは簡単に計算できて、すべて 2 でした。双子素数が先に存在する以上は $b_n$ の値は常に 2 になることは明らかです。

しかし、次の $b_7$ を計算するときに、問題が生じます。

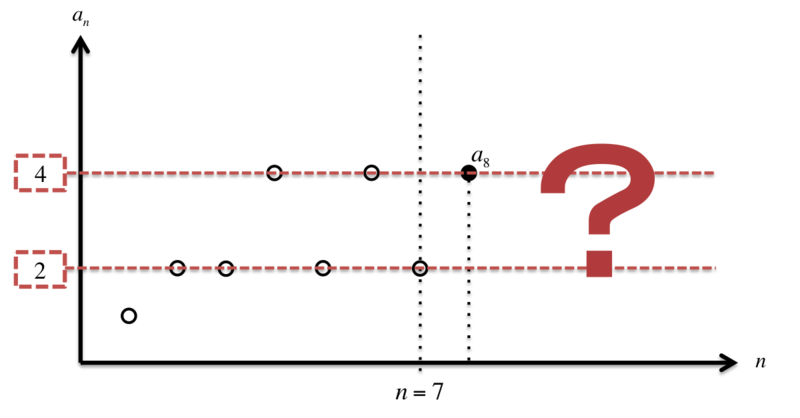
f:id:tsujimotter:20141203011119p:plain:w400

$b_7$ は 2 でしょうか。それとも 4 なのでしょうか。
もし、双子素数が有限で、かつ、これ以降登場しないのであれば、 $a_8 = 4$ が下限ですから $b_7 = 4$ です。一方、この先も双子素数が存在するのであれば $b_7 = 2$ となります。

少し先まで計算すると、

$a_{10} = p_{11} - p_{10} = 31 - 29 = 2$ （双子素数）

となって、双子素数は存在しますから、めでたく $b_7 = 2$ と決まりました。

一般に、 $n$ 番目以降の素数がどのように分布しているかがわからないと、 $b_n$ の値は決まりません。当然 $n$ が無限に大きくなったとき $b_n$ が収束する値もわかりません。

双子素数予想の話に戻って考えると、双子素数が無限に存在するのであれば（すなわち、終わりがなければ）、 $b_n$ はいつまでも 2 のままです。

すなわち双子素数予想は、次の式で言い換えることが出来ます。

《双子素数予想の言い換え》

$\displaystyle \liminf_{n\to\infty} \left(p_{n+1} - p_n\right) = 2$

右辺の値は、素数の分布に対してどの程度情報を持っているかの指標とも言えるでしょう。

結局、定理の意味するところは

現在、人類は双子素数予想を証明できていません。したがって、右辺はまだ 2 であると言い切れないわけです。

もしかすると、2 でないかもしれないのです。
この状況を説明するために、この式を使って考えを拡張しましょう。

たとえば双子素数は有限だったとして、差が 4 になるような連続する素数の組は無限に存在したとすると、

$\displaystyle \liminf_{n\to\infty} \left(p_{n+1} - p_n\right) = 4$

が成立します。

たとえば、双子素数は有限で、さらに差が 4 になるような連続する素数の組も有限個しか存在せず、一方で差が 6 になるような連続する素数の組は無限個存在するとしたら、

$\displaystyle \liminf_{n\to\infty} \left(p_{n+1} - p_n\right) = 6$

です。

ここで最初のメイナード博士の定理は次の式でした。

$\displaystyle \liminf_{n\to\infty} \left(p_{n+1} - p_n\right) \leq 600$

右辺が 600 で左辺がそれ以下になっているということは、すなわち、「差が $N$ となるような連続する素数の組が無限個存在する」が成り立つような $N$ が少なくとも 600 以下に１つは存在する、というわけです。

その $N$ がどんな値を取るか分かりませんが、少なくとも $N$ が 600 以下であることがわかりました！もし 2 だったとしたら双子素数予想の成立です！

何がすごいのか？

少し背景を説明しましょう。

双子素数予想の目標は右辺は 2 に一致することを示すことでした。しかしながら、つい最近まで右辺が有限で押さえられるかどうかすらわかっていなかったのです。

2013年4月17日に、ニューハンプシャー大学の張益唐博士が、この式が有限で押さえられることを示しました。そのときの評価式は、

$\displaystyle \liminf_{n\to\infty} \left(p_{n+1} - p_n\right) \leq 70,000,000$

とかなり雑多な見積もりでしたが、それでも大きな一歩でした。

ジェームズ・メイナード、テレンス・タオの両博士は、そのわずか半年後、右辺の評価式を 600 にまで減らしてみせたのです。メイナード博士によると、さらに Elliott-Halberstam 予想を仮定すると、右辺を 12 まで減らすことが出来るようです。

今まさに、ぐんぐん精度が上がっています。このままいけば、右辺を 2 にして双子素数予想が解けるかもしれない！そんな期待があるわけです。

双子素数予想は、ギリシア時代から知られている予想ですが、二千年たった今も解かれていない超難問です。難問と言えば、フェルマー予想が1995年、ポアンカレ予想が2003年に解決されましたが、双子素数予想は、このどちらの問題とは比べ物にならないぐらい難しい問題であると言われています。

ドラマの影響かわかりませんが、素数に関するニュースが出ると、すぐ暗号と結び付けて、実生活で役に立つかどうかで判断されがちです。しかし今回のように、純粋に数学的価値が存在するような問題もあるのです。
（もちろん暗号と無関係とまではいいませんが。）

ところで「プレプリント」って何？

以上で話の大枠は終わりですが、最後にタイトルの回収をして終わりたいと思います。

今回のジェームズ・メイナード博士の原稿ですが、（最初に触れた通り）これは論文ではありません。通常《論文》とは「《論文誌》に投稿され、その論文誌の《査読者》によって内容が正しいものと認められたもの」のことを言います。今回の原稿は、論文誌に投稿されたものではありませんから、論文ではないのです。

今回のものは一般に「プレプリント」と呼ばれるものです。プレプリントは、論文投稿前にインターネット上に事前公開された論文原稿のコピーのことをいいます。
論文誌に投稿して査読されるプロセスは、一般にかなり時間がかかります。短いもので数ヶ月、長いもので２年以上かかるものもあります。最近の傾向として、論文誌への投稿を準備しつつ、プレプリントとしてコピーをインターネット上に公開することが増えています。そうすることで、自分の成果をいち早く全世界に公開することが出来ます。また、その研究内容がインパクトのあるものであれば、その投稿した内容は全世界の研究者の目で正しいかどうかチェックされるわけです。

今回のメイナード博士の原稿をダウンロードした「arXiv」は、こうしたプレプリントを公開するためのウェブサイトです。過去にも、多くの重要な論文がこのarXiv上で事前公開されています。ポアンカレ予想を解いたペレルマンの論文もarXivで公開されました。（彼は結局論文誌に投稿しませんでしたが。。。）

というわけで、今回のメイナード博士のプレプリントはまだ論文になっていませんから、まだ正しいとは言い切れません。その点だけご注意を。調べた限りでは、まだ論文になっていないようなので、論文として公開されるのを楽しみに待ちましょう。

追記：2020/10/08
2015年1月のAnnals of Mathematics誌に論文として掲載されていたみたいですね。
https://annals.math.princeton.edu/2015/181-1/p07

それでは、ずいぶんと長くなってしまいましたがこの辺で終わりにしたいと思います。
読んでくださってありがとうございました。

「明日話したくなる数学豆知識」は明日も続きます〜♪

参考文献

プレプリントに対する反応が togetter にまとまっています。

素数の新定理発見！！極端な偏りなく分布？ - Togetter

実は 2ch 的なところではかなり話題になっていました。

【科学】米英数学者が素数に関する新定理発見！「素数はある間隔で極端な偏りなく分布している」・・・素数の法則が解明されれば暗号システム崩壊の危機も！？ : 旬話速報
 【科学】素数の間隔で新定理発見極端な偏りなく分布、米英数学者
 【数学】「素数」がどのような間隔で分布するかに関する新たな定理を発見、数学者からは「教科書を書き換える」との声も
 http://nanik.blog.jp/archives/37335923.html

ブログ記事ですが、ここも詳しいです。