久しぶりに整数論の調べものをしていたら,思った以上に捗って理解が深まったので,さっそく記事にしてみました。
約一年ぶりに「フェルマーの二平方定理」の記事の続きをお話ししたいと思います。
フェルマーの二平方定理 - tsujimotterのノートブック
目標
上の記事では,以下の証明を行いました。
ただし, は奇素数,
は正の整数です。この証明は高校レベルの簡単な整数論で証明できましたね。
一方,逆が成り立つことは,まだ証明していませんでした。フェルマーの二平方定理は,この両方が成り立つことを主張している定理です。
すなわち,今回の記事で証明したいことは,こういうことです。
つまり, 型の素数であれば,必ず2つの平方数の和に分解できる,という主張です。分解できないような
型の素数は存在しない,とも言えます。
ただし,完全な証明はせず,以下の法則が成り立つことを仮定します。
平方剰余の第一補充則:
右辺の記号は,ルジャンドル記号と呼ばれる記号ですが,この定理を仮定している訳ですから,平方剰余は知っているものとして進めます。
この仮定を置く理由は,フェルマーの二平方定理は,まさに平方剰余の補充則と同値である,ということを明確に示すためです。この仮定が成り立ちさえすれば,フェルマーの二平方定理も成り立つ,そういうことをこの記事では主張したいのです。
早速いきましょう。
平方剰余と  の平方根
の平方根
と,上で言ったばかりですが,やっぱり少しだけ仮定の意味について触れておきましょう。
上の命題の右側に関してですが,
この意味は「 は
の平方剰余である」ということでした。すなわち,
となるような が少なくとも1つ存在する,ということです。
そのような関係を満たす のうち,1つを
と置くことにしましょう。記号は本当のところ何でもよいのですが,
と置くことでまるで「虚数単位」のように見えて,都合が良いのです。
は上の式を満たすので,
となります。ね,まるで虚数単位でしょう。もちろん,虚数単位そのものではないので,複素数になったなんて思わないでください。 は,何度もいうように
のいずれかです。
たとえば, の場合,
ですから, または
が
の候補です。
と置いた場合は,
となります。
結局のところ,ここで言いたいことは,
は,
と同値である,ということです。
証明
さぁ,ようやく準備は整いました。証明に移りましょう。
目的は が存在するならば,
となるような
の組が存在する,ということです。
前段階として,まず以下の補題を証明します。
が存在するならば,

となるような
の組が存在する。ただし,
,
である。
まず, ,
の範囲において,
の組を全探索して考えます。「
以下」という範囲にした理由は,後々【伏線】として明かされます。
を横軸,
を縦軸として図にすると,このような範囲を探索していることが分かります。
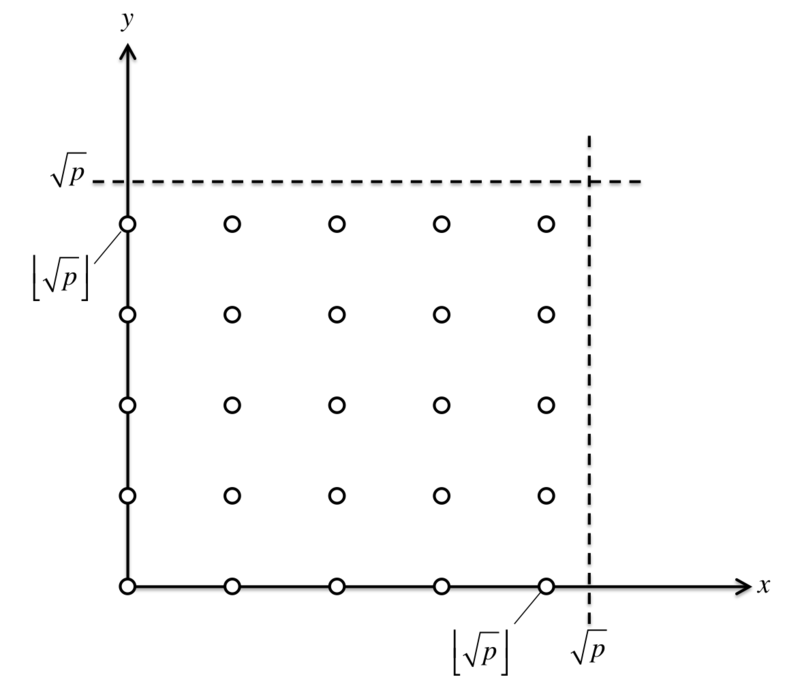
図のそれぞれ格子点が「該当する の組」を表しています。
さて,この格子点の個数は ですから,この数は
より大きい数です。つまり,
より大きい数の格子点が存在します。
一方で, という数を考えます。この
は法
において,
から
までの数の
個のうち,いずれかの値をとります。
ここで「鳩ノ巣原理」が活躍します。
より大きい数だけ存在する
の組を,
個の値のいずれかに割り当てるわけですから,少なくともいずれか2つの組は
を法として合同になるはずです。
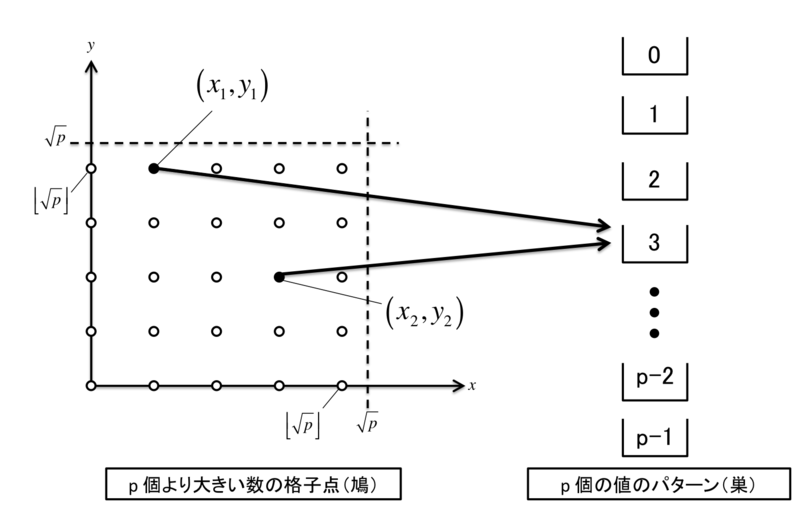
したがって,その組を と
とします。すると,これらで作った
と
は
を法として合同ですから,
となります。移項すると,
です。改めて ,
とおくと,
となる。ここで, は異なる格子点より,
であるから,補題が示せた。
いやー,見事な論法ですね。tsujimotter はこういう証明が大好きです。具体的に数を示さないのにも関わらず,そういう数が存在することだけは証明できてしまう。まさに,鳩ノ巣原理がうまくはまった例ですね。
さて,続きを証明してしまいましょう。
先の補題の両辺に, をかけます。すると,
が成り立ちます。
展開すると,
仮定 より
一方, かつ
より,
したがって,
ただし, である。
あとは「 が
以上ではないこと」を示せば,証明完了です。このためには,冒頭から温めてきた【伏線】が使えます。
かつ
より,
である。
同様に, かつ
より,
したがって,
よって は
以上ではありえない。すなわち,
であることが示せた。
まとめ
いかがだったでしょうか。
平方剰余の第一補充則だけを仮定して, 型の素数
が,平方数の和
で表せることを示しました。このことから,フェルマーの二平方定理は,まさに平方剰余の第一補充則に依存した定理であることが分かるでしょう。
証明の流れも面白かったですね。「鳩ノ巣原理」を使って,具体的な数を構成することなく,都合のよい数の組が存在することだけを示したり。あとは, をまるで,虚数単位のように使って,複素数の積のように数を分解したり。
の条件付けも見事でした。
ちなみに,今回はやらなかったですが, を具体的に構成する方法もあります。「フェルマーの無限降下法」をベースとした方法ですが,これも気が向いたらやってみたいと思います。もっとも,tsujimotter は今回の記事を書けたことで,だいぶ満足してしまっていますが。笑
それでは,今日はこの辺で。
参考文献
今回の証明は,以下の小山信也先生の文献を参考に構成しました。この文章は,冒頭のエピソードがとても素敵です。たとえ中身がわからなくても,冒頭だけでも読む価値はあります。