ラマヌジャンの円周率近似式と連分数展開

シュリニバーサ・ラマヌジャンといえば、インドの魔術師の異名を取る数学者で、魔術的な数式をたくさん発見していることで知られています。

ラマヌジャンは円周率 $\pi$ についても多様な式を発見しています。その発見の一つとして

$\displaystyle \pi \fallingdotseq \sqrt[4]{\frac{2143}{22}} \tag{1}$

という近似式をご存知の方は多いと思います。

この近似式の精度は驚くほどよいのですが、右辺を計算してみると

$\displaystyle \sqrt[4]{\frac{2143}{22}} = \underline{3.14159265}258\ldots$

となります。下線部が円周率と一致していますが、なんと小数点以下8桁まで一致しています。

有名な円周率の近似式として

$\displaystyle \pi \fallingdotseq\frac{22}{7} = \underline{3.14}2857\ldots$ （約率）

$\displaystyle \pi \fallingdotseq\frac{355}{113} = \underline{3.141592}92\ldots$ （密率）

などの式がありますが、これらと比べてもかなり精度が高いことが分かります。
（前者は「約率」、後者は「密率」という名前がついています。）

約率・密率については以前紹介したことがありました：
tsujimotter.hatenablog.com

この $22/7$ や $355/113$ については、後で述べるように連分数展開がその背景にあります。

一方で、ラマヌジャンの円周率近似式については特に数学的な背景もなさそうで、単なる偶然の産物だろうと思っていました。
（ラマヌジャンは偶然の産物を見つけるのも得意です。）

ところがなんと、ラマヌジャンの円周率近似式にも数学的な背景があったようなのです。しかも、（ $22/7$ や $355/113$ と同じく）連分数展開が背景にあったようなのです。これが今日のメインテーマです。

また、記事の最後には、今回の方法を応用した類似の近似式を見つける方法についても書いています。

とても面白いのでぜひ最後まで読んでいただければと思います！

目次：

1. 連分数展開とは

2. 【宣伝】小数の連分数展開を計算するプログラム

3. 約率 22/7 と密率 355/113 の秘密

4. 連分数展開の近似分数が高精度なわけ

5. ラマヌジャンの近似式の秘密

6. 他にも作れる？（自由研究）

追記：近似値ルート10

謝辞と関連書籍

関連記事

1. 連分数展開とは

連分数展開とは、正の実数 $\alpha$ があったときに、正の整数列 $a_0, \; a_1, \; a_2, \; a_3, \; \ldots$ を用いて

$\displaystyle \alpha = a_0 + \cfrac{1}{a_1 + \cfrac{1}{a_2 + \cfrac{1}{a_3 + \cfrac{1}{\ddots}}}} \tag{2}$

のように表すことをいいます。繰り返し分数で表すことから、連分数展開といいます。ただし、この展開は必ずしも無限回続かなくても、有限回で止まって

$\displaystyle \alpha = a_0 + \cfrac{1}{a_1 + \cfrac{1}{a_2 + \cfrac{1}{a_3 + \cfrac{1}{\ddots + \cfrac{1}{a_n}}}}}$

のようになってもよいものとします。

正確にいえば

$\displaystyle \alpha = a_0 + \cfrac{b_1}{a_1 + \cfrac{b_2}{a_2 + \cfrac{b_3}{a_3 + \cfrac{b_4}{\ddots}}}}$

のように表すことを連分数展開といいます。

今回の連分数展開は、分子の $b_1, b_2, b_3, \ldots$ がすべて $1$ であるものを考えています。これを正則連分数展開といいます。

連分数展開は、紙面（ページ画面？）を大きく使うので、式 $(2)$ のような連分数展開を簡単に

$[a_0; a_1, a_2, a_3, \ldots]$

のように表すことも多いです。今回もこの記法を用います。すなわち

$[a_0; a_1, a_2, a_3, \ldots] = a_0 + \cfrac{1}{a_1 + \cfrac{1}{a_2 + \cfrac{1}{a_3 + \cfrac{1}{\ddots}}}}$

ということですね。

さて、任意の正の実数はこのように連分数展開で表すことができます。今回のテーマである円周率 $\pi$ を例に、その計算方法を紹介しましょう。

まず、円周率 $\pi$ を次のように小数展開しておきます：

$\pi \fallingdotseq 3.141592653589793$

①整数部分を $a_0$ とします：

$a_0 = 3$

整数部分を引いた残りの逆数を取ります。

$\displaystyle \frac{1}{3.141592653589793 - a_0} = \frac{1}{0.141592653589793} \fallingdotseq 7.062513305931052$

②再び整数部分を $a_1$ とします：

$a_1 = 7$

整数部分を引いた残りの逆数を取ります。

$\displaystyle \frac{1}{7.062513305931052 - a_1} = \frac{1}{0.0625133059310529} \fallingdotseq 15.996594406684103$

③再び整数部分を $a_2$ とします：

$a_2 = 15$

整数部分を引いた残りの逆数を取ります。

$\displaystyle \frac{1}{15.996594406684103 - a_2} = \frac{1}{0.996594406684103} \fallingdotseq 1.0034172310150002$

以下同様に
「整数部分を $a_n$ とし、小数部分の逆数を取る」
という操作をひたすら繰り返すことで、 $a_3, a_4, a_5, \ldots$ を順次得ることができます。

実際、円周率 $\pi$ について $a_0$ から $a_{10}$ まで計算を繰り返すと

$\pi = [3; 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, \ldots] \tag{3}$

という連分数展開が得られます。

実際に連分数の形にすると、次のようになります：

$\displaystyle \pi =3 + \cfrac{1}{7 + \cfrac{1}{15 + \cfrac{1}{1 + \cfrac{1}{292 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{2 + \cfrac{1}{1 + \cfrac{1}{3 + \cfrac{1}{\ddots}}}}}}}}}}}$

今回は有効数字が有限桁の小数展開を用いて計算しているので、無限項の連分数展開を厳密に求めることはできません。

より項数の大きな連分数展開を求めようとするならば、元々の小数展開の有効数字の桁数を大きくする必要があります。

また、 $\alpha$ が有理数の場合は、その連分数展開は有限回で止まります。逆に無理数の場合は、有限回では止まらず、無限に続くことになります。

2. 【宣伝】小数の連分数展開を計算するプログラム

さて、今回の連分数展開の計算を実行したり、近似分数の計算をするのは少し骨が折れますね。

そこで、小数の連分数展開を計算するプログラムを作って公開しました。
tsujimotter.info

正の小数 $\alpha$ と、連分数展開により近似したい項数 $n$ を入力すると、その計算結果を表示してくれます。

今回の記事の内容の検証や、皆様方の自由研究にぜひお使いください！

3. 約率 22/7 と密率 355/113 の秘密

さて、円周率の連分数展開

$\pi = [3; 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, \ldots] \tag{3再掲}$

が得られました。

ここから円周率の有名な近似式である

$\displaystyle \pi \fallingdotseq\frac{22}{7} = \underline{3.14}2857\ldots$ （約率）

$\displaystyle \pi \fallingdotseq\frac{355}{113} = \underline{3.141592}92\ldots$ （密率）

を導出してみましょう。

(a) 約率
$\pi$ の連分数

$\pi = [\underline{3; 7}, 15, 1, 292, 1, 1, 1, 2, 1, 3, \ldots]$

について、下線部のところだけ残したものが、約率に一致します：

$\displaystyle \begin{align*} [3; 7] &= 3 + \cfrac{1}{7} \\ &= \frac{22}{7} \end{align*}$

(b) 密率
$\pi$ の連分数

$\pi = [\underline{3; 7, 15, 1}, 292, 1, 1, 1, 2, 1, 3, \ldots]$

について、下線部のところだけ残したものが、今度は密率に一致します：

$\displaystyle \begin{align*} [3; 7, 15, 1] &= 3 + \cfrac{1}{7 + \cfrac{1}{15 + \cfrac{1}{1}}} \\ &= 3 + \cfrac{1}{7 + \cfrac{1}{16}} \\ &= 3 + \cfrac{16}{113} \\ &= \frac{355}{113} \end{align*}$

こんなわけで、連分数展開を途中までで止めた連分数を計算すると、円周率の近似式ができるのです。面白いですね。

4. 連分数展開の近似分数が高精度なわけ

ところで約率や密率などの近似式は、単なる近似式ではなく、特に精度の良い近似式なのでした。実は、これらの近似式の精度が高い理由も連分数展開の持つ性質によって説明できます。

一般に、正の無理数 $\alpha$ の連分数展開

$\alpha = [a_0; a_1, a_2, a_3, \ldots ]$

を $n$ 項目で打ち切って得られる既約分数の分子・分母をそれぞれ $p_n, \; q_n$ とします。すなわち

$\displaystyle [a_0; a_1, a_2, a_3, \ldots , a_n ] = \frac{p_n}{q_n} \tag{4}$

とすると、元の数 $\alpha$ と近似分数 $p_n / q_n$ の誤差

$\displaystyle \left|\alpha - \frac{p_n}{q_n}\right|$

を考えたときに、これが「ある意味で最も小さく」なるような「最良の」近似分数になるのです。

具体的には、次の事実が成り立ちます：

定理1（連分数展開の近似分数の最良性）

$\alpha$ を無理数とし、 $\alpha$ の連分数展開の第 $n$ 近似分数を $p_n / q_n$ とする。このとき、任意の $\displaystyle \frac{p_n}{q_n} \neq \frac{p}{q}$ かつ $q \leq q_n$ なる分数 $p/q$ に対して

$\displaystyle \left| \alpha - \frac{p_n}{q_n}\right| < \left| \alpha - \frac{p}{q}\right|$

が成り立つ。

つまり、元の誤差が最も小さい近似になっているというわけです。このような性質を(第1種)最良近似といいます。分母を大きくすれば、いくらでも近似精度を上げることは原理的に可能なので、 $q < q_n$ なる条件は必要ですね。

連分数展開による近似分数は(第1種)最良近似という性質を持っています。

円周率 $\pi$ の連分数展開 $\pi = [3; 7, 15, 1, 292, \ldots]$ について、第0〜第4近似分数を以下に示します：

$\displaystyle [3] = \underline{3}$
$\displaystyle [3; 7] = 3 + \cfrac{1}{7} = \frac{22}{7} = \underline{3.14}2857\ldots$
$\displaystyle [3; 7, 15] = 3 + \cfrac{1}{7 + \cfrac{1}{15}} = \frac{333}{106} = \underline{3.1415}094339\ldots$
$\displaystyle [3; 7, 15, 1] = 3 + \cfrac{1}{7 + \cfrac{1}{15 + \cfrac{1}{1}}} = \frac{355}{113} = \underline{3.141592}9203\ldots$
$\displaystyle [3; 7, 15, 1, 292] = 3 + \cfrac{1}{7 + \cfrac{1}{15 + \cfrac{1}{1 + \cfrac{1}{292}}}} = \frac{103993}{33102} = \underline{3.141592653}0\ldots$

ところで、連分数展開の精度が高いのであれば、約率や密率でなくても用は足りそうです。しかしながら、最良近似分数の中にも精度の良し悪しはありそうです。

ここで注目したいのは、連分数展開の数列の各項の大きさです。

$\require{color} \displaystyle \pi = 3 + \cfrac{1}{7 + \cfrac{1}{15 + \cfrac{1}{1 + \color{red} \cfrac{1}{292 + \cfrac{1}{\ddots} \color{black} }}}}$

たとえば、 $[3; 7, 15, 1]$ で打ち切ると、赤色以降が無視されるわけですね。すると $\frac{1}{292 + \ddots}$ の部分がなくなるわけです。 $292$ という項は比較的大きな数なので、 $1/292$ は小さい数になります。したがって、 $\alpha$ と $p_n/q_n$ の差は小さくなる（精度がよくなる）わけです。

つまり、連分数展開の数列において、大きい数が出た直前で打ち切った近似分数を作ると、精度がよくなるというわけです。

以上のことは直感的にも明らかな気がしますが、これを裏付けるのが次の定理2です：

定理2（近似分数の質）

$\alpha$ を正の実数とし、 $\alpha$ の連分数展開 $[a_0; a_1, a_2, a_3, \ldots ]$ の第 $n$ 近似分数を $p_n / q_n$ とする。このとき

$\displaystyle \left|\alpha - \frac{p_n}{q_n}\right| = \frac{1}{q_n^2 \lambda_n} \tag{5}$

が成り立つ。ここで、 $\lambda_n$ は

$\displaystyle \lambda_n = a_{n+1} + \cfrac{1}{a_{n+2} + \cfrac{1}{a_{n+3} + \cfrac{1}{\ddots}}} + \cfrac{1}{a_n + \cfrac{1}{a_{n-1} + \cfrac{\ddots}{\ddots + \cfrac{1}{a_1}}}}$

である。

$\lambda_n$ が複雑な形をしていますが、3項の和になっていて、先頭の項が $a_{n+1}$ で残り2項が1より小さいことが分かれば十分です。したがって、 $\lambda_n$ はだいたい $a_n$ になります。

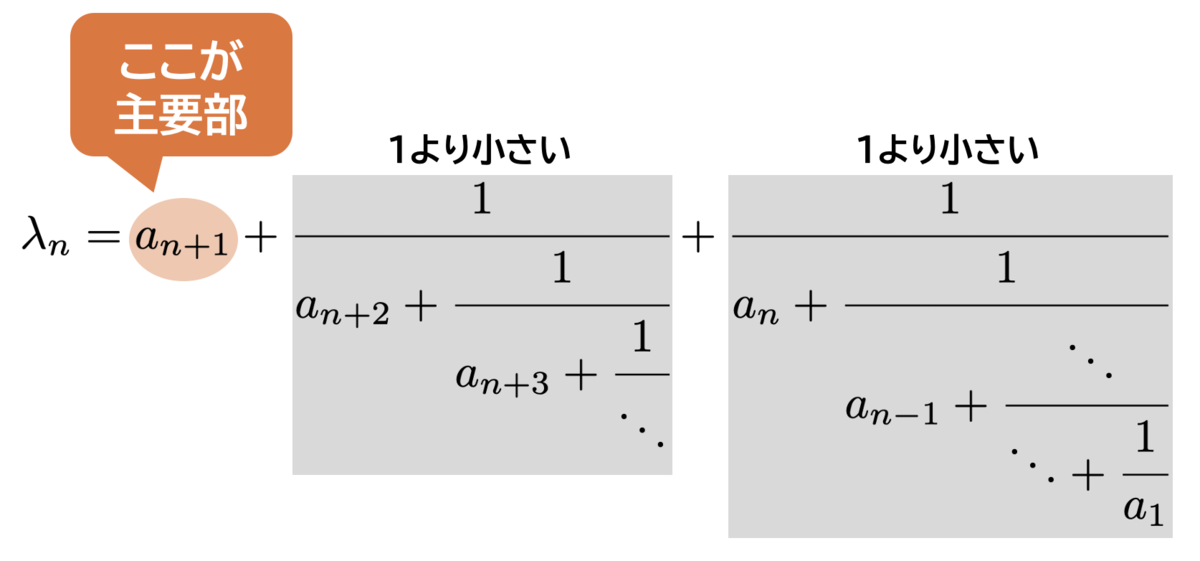
より正確には

$\lambda_n > a_{n+1}$

が成り立ちます。よって、式 $(5)$ より

$\displaystyle \left|\alpha - \frac{p_n}{q_n}\right| = \frac{1}{q_n^2 \lambda_n} < \frac{1}{a_{n+1} q_n^2}$

が成り立ちます。この式から、 $a_{n+1}$ が大きければ大きいほど、 $p_n / q_n$ の精度が良くなることが分かりますね。

以上のことから、約率や密率の精度の良さが説明できます。

$[\underline{3; 7}, \color{red}{\bf 15}, \ldots \color{black}]$ （約率は下線部までで近似）
$[\underline{3; 7, 15, 1}, \color{red}{\bf 292}, \ldots\color{black}]$ （密率は下線部までで近似）

約率は $a_2 = 15$ の直前で、 $a_4 = 292$ の直前で打ち切っているので、精度が高いというわけです。

5. ラマヌジャンの近似式 $\sqrt[4]{\frac{2143}{22}}$ の秘密

さぁ、いよいよ本題のラマヌジャンの近似式の秘密について解説したいと思います。

$\displaystyle \pi \fallingdotseq \sqrt[4]{\frac{2143}{22}} \tag{1再掲}$

ところで、この式の右辺は純粋な分数の形をしていませんので、そのままでは連分数展開は使えないように思えます。

ここで一捻りが必要なのですが、両辺を4乗して考えれば良いのです。つまり、 $\pi^4$ の連分数展開を計算して、その近似分数を求めれば良いわけですね。

実際、 $\pi^4$ の連分数展開は次のようになります：

$\pi^4 = [97; 2, 2, 3, 1, {\bf 16539}, 1, 6, 3, 2, 3, \ldots ]$

分かりやすく連分数の形に表示すると次のようになります：

$\displaystyle \pi^4 = 97 + \cfrac{1}{2 + \cfrac{1}{2 + \cfrac{1}{3 + \cfrac{1}{1 + \cfrac{1}{{\bf 16539} + \cfrac{1}{1 + \cfrac{1}{6 + \cfrac{1}{3 + \cfrac{1}{2 + \cfrac{1}{3 + \cfrac{1}{\ddots}}}}}}}}}}}$

さて、ここで目を引かれるのは 16539 という項ですね。これが他の項と比べて圧倒的に大きいので、（前節の理屈より）この前の項で打ち切った近似分数を作りたくなります。

そこで、次のような連分数を計算すると

$\displaystyle \begin{align*} [97; 2, 2, 3, 1] &= 97 + \cfrac{1}{2 + \cfrac{1}{2 + \cfrac{1}{3 + \cfrac{1}{1}}}} \\ &= \frac{2143}{22} \end{align*}$

となり、確かに $\displaystyle \frac{2143}{22}$ が得られました！

近似分数 $\displaystyle \frac{2143}{22}$ の精度を確認するために、 $\pi^4$ の小数展開を比較してみましょう。

$\displaystyle \begin{align*} \pi^4 &= \underline{97.40909}1034\ldots \\ \frac{2143}{22} &= \underline{97.40909}0909\ldots \end{align*}$

小数第5位まで一致していますね。さらにいうと、その下の桁も $10$ と $09$ なので、小数第7位程度の精度であることが分かります。

$1/22$ は循環節が2桁の小数なので、これが $\pi^4$ を近似するというのは少し不思議な感じがしますね。

これは4乗根をとる前なので、 $\frac{2143}{22}$ の4乗根をとると次のようになります：

$\displaystyle \sqrt[4]{\frac{2143}{22}} = \underline{3.14159265}258\ldots \tag{再掲}$

そんなわけで、ラマヌジャンの発見した近似式を自然な発想で導くことができたというわけですね。

ラマヌジャンは理屈の説明を残していないそうなので実際の考えは分かりませんが、ラマヌジャンの発想を追体験できた気分になって嬉しく思っています。

ところで、元の近似精度がよくても、4乗根をとったら精度が下がったりしないかと思う方もいるかもしれません。実際は、4乗根をとることで精度は上がるのですが、それは次の理由からです。

まず、 $\pi^4$ と近似分数 $p/q$ の差を $\varepsilon$ とおいて、 $\varepsilon$ は十分小さいものとします：

$\displaystyle \frac{p}{q} - \pi^4 = \varepsilon$

両辺の4乗根をとり、右辺を二項展開すると次のようになります：

$\displaystyle \begin{align*} \sqrt[4]{\frac{p}{q}} &= (\pi^4 + \varepsilon)^{\frac{1}{4}} \\ &= (\pi^4)^{\frac{1}{4}} + \frac{1}{4}(\pi^4)^{\frac{1}{4} - 1} \varepsilon + \cdots \\ &= \pi + \frac{1}{4\pi^3} \varepsilon + \cdots \end{align*}$

よって

$\displaystyle \sqrt[4]{\frac{p}{q}} - \pi = \frac{1}{4\pi^3} \varepsilon + \cdots$

となりますが、 $\cdots$ の部分は $\varepsilon$ の2次以上の項であり十分小さいため、誤差は $\frac{1}{4\pi^3} \varepsilon$ 程度になります。

ちなみにですが、今回の近似式 $\sqrt[4]{\frac{2143}{22}}$ には面白い応用があります。ルートと四則演算しか計算には必要としないので、定規とコンパスを使って作図できるのです。
intergers_blogのこちらの記事でその点が紹介されています。
integers.hatenablog.com

これはラマヌジャンによる「円積問題」への近似的アプローチとして知られています。