楕円曲線とは(細かいことを抜きにして言えば *1)
という式で表される曲線のことです。上の方程式のことを、楕円曲線の定義方程式といいます。
時と場合によって微妙に定義式の書き方が異なったりますが、左辺の の指数はいつも 2乗 になっていて、右辺の式はいつも決まって 3乗 になっています。
楕円曲線について勉強した人は、一度くらい、このような疑問を持つのではないでしょうか。
ところで、楕円曲線の定義として、以下のものを思い浮かべた方もいるかもしれません。
種数1の非特異射影代数曲線を楕円曲線という
上記の定義には、定義方程式の形が一切出てきませんが、冒頭の定義と一致するのでしょうか。
ここでは、種数1 という情報がポイントです。ほぼこの情報だけから、楕円曲線の定義方程式の形状が決定されるのです。
代数曲線の理論には、リーマン・ロッホの定理 という重要な定理があって、楕円曲線の上で定義される関数の空間の次元を、種数を用いて特定することができます。特定した関数の空間における関係式を用いて、定義方程式を決定することができるのです。
ざっくりと流れを説明しましたが、以降で詳しく解説します。
関数体とは
まずは 関数体 という概念を導入したいと思います。
代数幾何学という分野では、曲線とその上の関数という概念がセットで重要です。今回の記事の話が理解できると「曲線のことを知りたかったら、その上の関数を考えよう」というアプローチが自然であることが実感できるでしょう。
勿体振りましたが、関数体の説明をします。関数体とは、要するに「曲線の点に対して何か値を定める関数全体」のなす体のことです。
イメージしやすいように具体的な曲線を設定して説明することにしましょう。楕円曲線 を
とします。このとき、座標 としては複素数
の値をとるか、無限遠点をとるか、のいずれかとします。
(複素数を表すのは困難なので)実数の点に限った図を表すと、こんな感じになりますね。
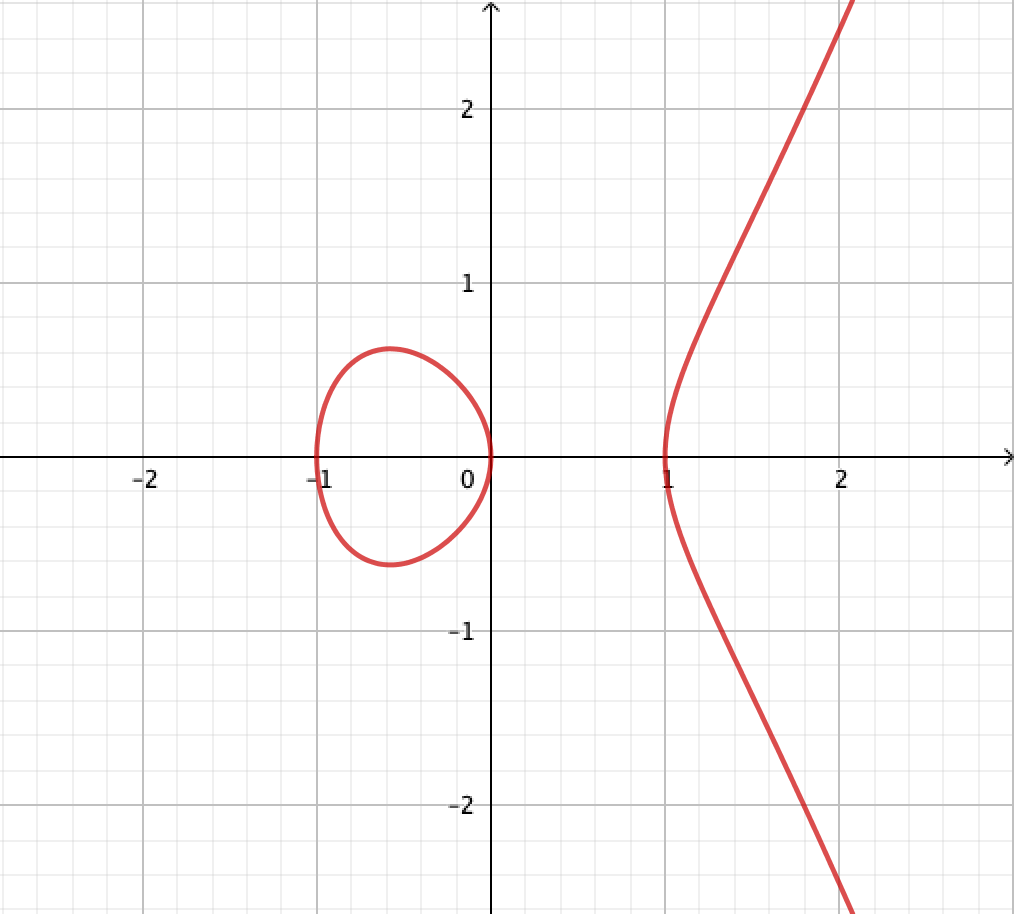
さて、この楕円曲線は、右辺が3次式になっています。因数分解すると
となります。したがって、 のとき、
となります。
ここで、 の点に名前をつけることにします。
座標の値が
であるような点を
とします。といっても、一般には2通りありますから、
座標が正の点を
として、
座標が負の点を
とします。つまり、こういうことです。

ここで、 のときは
となります。
となるような点のことを分岐点といいます。
なお、楕円曲線には無限遠点がありますが、これを と表記すると、
も分岐点となります。
次に、楕円曲線 の任意の点
に対して、その
座標を取り出す関数
を考えましょう。関数
は、
の点
に対して、複素数
を割り当てる関数だと思えます。
同様に、楕円曲線 の任意の点
に対して、その
座標を取り出す関数
を考えます。
この や
というのは、
の関数の一例です。「座標を取り出すという操作は
の関数である」という見方が重要です。
関数 を手に入れたら、これを組み合わせてさまざまな関数を作ることができます。
を変数とする
上の多項式
も の関数です。つまり、
上の任意の点
に対して、
として関数の値を定めることができます。
一方で、 は独立ではないことに注意します。
には
なる関係があるので、多項式関数に対してこれらを同一視するような関係を入れて、多項式環 を割ってあげる必要があります。
そこで、 の 座標環 を
と定義することにしましょう。これは、 の関係式を踏まえた、
の多項式関数全体を表す環だと思うことができます。
たとえば、 という関数は
と合同になります。
ということは、 の 2 次以上の項はすべて
の多項式で表せることになります。
つまり
と表せるということですね。
座標環の任意の元に対する(分母が0にならない)有理式、すなわち有理関数全体
も
の関数体
について、これから調べていくことにしましょう。
零点・極の位数
先ほど定義した の関数に、零点と極という概念を導入します。
関数 の 零点 とは、
となる点
のことです。また、
となる点
を
の 極 と言います。
たとえば、 という関数の零点を求めましょう。すなわち、
となる点を探します。先ほどの楕円曲線の図で
との交点を考えると、
でした。すなわち
です。このとき、関数 は
は 1位の零点 を持つといいます。
同様に、関数 の零点を求めましょう。すなわち、
となる点を探します。これは明らかに
ですね。すなわち
です。このとき、関数 は
で 2位の零点 を持つといいます。これは、
であり、重なった2つの点で零点を持つと言うことで、合わせて 2 位というような計算です。
(こんな感じで、関数が分岐点に零点を持つ場合は、位数は2以上となります。)
また、 の極を求めたいのですが、関数
は
で極を持ちます。これはつまり、無限遠点では
は 0 になるということですね。そのときの位数は(天下り的ですが)
となります。
の極も同様に
に極を持ち、(結論だけを言うと)その位数は
となります。*2
重要な結論なので、以上をまとめておきましょう。
- 関数
は
で
位の零点を持ち、
で
位の極を持つ。
- 関数
は
で
位の零点を持ち、
で
位の極を持つ。
ここで重要な観察事実として、どちらの関数でも
となっていることに注意します。これは今回の記事で直接関係しませんが、続編の記事ではこのことを使う予定です。
また、関数 を考えましたが、
と
を組み合わせた多項式や有理関数も同様に位数を計算できます。
たとえば、 は
にそれぞれ位数
の極を持ちます。このとき
という関数は、 に位数
の極を持ちます。
商を考えると
位数 の極を持つ関数ができます。
また、和や差をとると、位数が大きい方になります。
この場合、極の位数は となります。
こんな要領で、 の有理関数、すなわち関数体の任意の元の位数を決定することができます。
ベクトル空間 
位数の説明ができたので、 に特定の位数の極を持つような関数全体の空間を考えたいと思います。
自然数 に対して
を
とします。たとえば、 には、
において位数 0 か 1 か 2 か 3 を持つ関数が入るというわけです。
ここで という空間は、単なる関数の集合なだけでなく、
ベクトル空間 でもあります。これが極めて重要です。ベクトル空間なので次元という量が定義できます。次元が定義できると、ベクトル空間についてのかなりの情報がわかるのです。
ベクトル空間 の次元
を計算できるのが、リーマン・ロッホの定理 です。
リーマン・ロッホの定理は、曲線の 種数 と、標準因子という概念を使って、上記のベクトル空間の次元を決定する公式を与えます。なお種数は、今回は楕円曲線を考えているので、 であると考えてください。
残念ながら、今回の記事では「因子」という概念を定義できないので、リーマン・ロッホの定理のフルステートメントを書くことができません。
以下では、今回のケースに特化した限定的なリーマン・ロッホの定理の系を紹介したいと思います。今回の目的では、限定的な主張でも十分だからです。
それでは、リーマン・ロッホの定理の威力をお見せしましょう。まず、今回のケースでは なので
とかけることに注意します。
のときはリーマン・ロッホより
です。したがって、基底は1つです。 また、明らかに定数関数は極を持たないので、
の元になります。したがって
であることがわかります。
たったこれだけで決定できてしまうのです!
次に のときはリーマン・ロッホより
です。したがって、基底は2つです。ここで、明らかに定数関数は
の元です。よって、基底の一つは
です。もう一つの基底ですが、我々は「
で位数2の極を持つ関数」を一つ知っています。関数
ですね!よってこれがもう一つの基底となって
が言えます。
同様に のときを考えましょう。リーマン・ロッホより
であり、3つのうち2つの基底は
です。もう一つの基底ですが、これは「
で位数3の極を持つ関数」ですから、すなわち関数
です!よって
が言えます。
いやーすごいですね!
ベクトル空間の性質により、次元が決定できれば空間の構造が決定できてしまいます。その次元を決定できるのがリーマン・ロッホなわけですから「リーマン・ロッホすごい!」というわけですね。
さらに続きます。
のとき、リーマン・ロッホより
です。ここで新しい基底ですが、
を考えましょう。
は、極の位数が 2 ですが、かけ合わせると位数が
となります。よって
が言えます。
同様に のとき、リーマン・ロッホより
です。
を考えると、これは
が位数となります。よって
が言えます。
最後に で終わりにしましょう。リーマン・ロッホより
です。
を考えると、これは
が位数となります。よって
が言えます。
楕円曲線はなぜ3次曲線で表せるのか?
さてここで、この記事でもっとも重要な帰結が得られました。
定義を思い出すと、 の定義は
でした。
ところで、 という関数を考えると
より、位数 の極を持ちます。つまり
というわけです。
ということは、 という関数は、右辺の6つの基底を使って
(ここで、
と表せるはずです!おおっ、これは右辺が の3次式になって、左辺が
の2次式になっていますから、定義方程式の形にかなり近いですね!
の係数
が
でないことが気になるかもしれませんが、その場合は
と変換することで、 とできます。他の係数も適当な変数変換で消すことができるので、冒頭の楕円曲線の定義方程式が得られます!すごい!!
係数の消し方の方法はこちらに乗っていました。
http://wasmath.la.coocan.jp/weierstrass_form.pdf
楕円曲線が、 が 2 次で、
が 3 次だったわけは
という式にあったというわけです!
面白いですね!
見方を変える
この辺で話を終わりにしたいところですが、一つ気になる点があります。
今回の話は、種数1である曲線からスタートして、リーマン・ロッホの定理を使って の各次元を決定しました。そこから
の基底を具体的に決定することで、元々の曲線の定義方程式を得ることができました。
以上によって
ところがです。ここでよーく手順を思い出していただきたいのですが、 を決定する手順で、少しまずい点があるのです。
関数 の位数の情報を使ってしまっている点です。あらかじめ計算した
の位数は、あらかじめ定義方程式を与えた上で計算した結果でした。
つまりこういうことです。
という流れになってしまって、今回の「定義方程式を与える」という目的からすると、循環論法になっています。
循環論法になってしまいました。これじゃあダメだ、と諦めてしまいそうですが、回避する方法があります。それは、 という関数を一切使わない という方法です。
議論の流れを思い出します。リーマン・ロッホを使って、 が計算できるところまではオーケーです。
ですが、リーマン・ロッホより
が得られるまではいいでしょう。ここで、定数関数
は
に属するのもオーケーです。
問題はこの次です。関数 を使ったのがまずかった点です。次のように考えましょう。
は次元の比較により
より真に大きいので、
の元
をとることができます。この元は、(
に入ってないので)極の位数が 2 でなければなりません。よって
が成り立ちます。
同様に、 を考えます。この場合も、
は次元の比較により
より真に大きいので、
の元
をとれます。この元は、極の位数が 3 でなければなりません。よって
が成り立ちます。
次以降の議論は、先ほどのものと同様で、以下のように計算できます。
これによって
から
(ここで、
という式を立てることができます。
ここで、関数 をそれぞれ座標とみなせば、上の式は楕円曲線の定義方程式を与えていると思うことができるでしょう。
以上の流れで、先ほどの循環論法の問題を回避することができました。
今回の記事を書くにあたって、循環論法についてずいぶん悩みました。曲線の座標は「曲線上の点に対して値を返す関数である」という理解ができたことが大きくて、個人的なブレイクスルーでした。
まとめと次回予告
今回は楕円曲線の定義方程式を求める問題を扱いました。これまでの議論によって、楕円曲線の定義方程式における次数の謎が理解できました。今回の例を通して、「関数の性質から代数曲線の性質がわかる」という感覚も伝えられたんじゃないかなと思います。
具体的な流れとしては、まず関数体の部分ベクトル空間 を計算して、
における代数的な関係式を得ることができました。これによって定義方程式が得られるという話でした。次元の計算には、リーマン・ロッホの定理がその威力を発揮しましたね。
基底を計算する際には
というような素朴な式が現れた、というのも面白かったですね。
楕円曲線についての謎が一つ解けたわけですが、まだ謎が残っています。
たとえば、「加法」についてです。楕円曲線には、加法、つまり足し算が定義できることはよく知られています。一方で、あの加法の意味ってわかりますか?かなり不思議な定義をしていますよね。
次回は、楕円曲線の加法が「なぜあのような形で定義されるのか」について話したいと思います。そこでは、「因子」という概念が導入されますが、これは今回の関数体の議論の延長線上にあるものです。お楽しみに。
それでは今日はこの辺で。
参考文献
今回の記事は、以下の本の「超楕円曲線とヤコビ多様体」という章を参考にしました。

数論入門【現代数学への入門8】 (岩波オンデマンドブックス)
- 作者: 山本芳彦
- 出版社/メーカー: 岩波書店
- 発売日: 2018/04/10
- メディア: オンデマンド (ペーパーバック)
- この商品を含むブログを見る
以下のPDFも勉強したいと思っていて、ブログのいくつかの記述はこちらを参考にしています。
小川裕之 : 代数曲線の Riemann-Roch の定理 - 第 15 回 整数論サマースクール 《種数の高い代数曲線と Abel 多様体》報告書
http://www2.meijo-u.ac.jp/~yonishi/research/pub/ss2007/02ogawa.pdf
謝辞
この話に興味を持った最初のきっかけはmattyuuさんのこの発表です。素敵な発表をありがとうございます。
www.nicovideo.jp
続きを公開しました(2019/07/04追記)
*1:楕円曲線の定義としては、正確に言えば以下のものです。
楕円曲線とは、
①非特異な射影曲線であって
②上の式に双有理同値な曲線のこと
です。
さらに言えば、係数体の標数が2でも3でもない場合はこれでよいのですが、標数が2や3の場合には ではなく
という式に双有理同値な曲線を楕円曲線といいます。
が、今回は細かいところを抜きにして、標数 0 のものだけを考えます。その上で、
で表された曲線のことを楕円曲線ということにしましょう。
*2:関数体の零点や極の位数について、少し歯切れの悪い説明になっているのは、私が定義を理解できていないためです。
実際、位数は次のように定義されるそうです。座標環 の「点
における局所環
」を考えると、これが離散付値環になります。
の付値から誘導される関数体
の付値を
とします。
に対して、
のとき
は
で位数
の零点を持つといい、
のとき
は
で位数
の極を持つと定義されるようです。
この辺の意味するところを、私自身が解説できるほど理解していないため、今回はこの部分の解説を避けることにします。
の位数については、結果的には、本文の通り計算できることを認めた上で進めたいと思います。