今回は「循環小数」の奥深い世界にご招待します。
これまでtsujimotterのノートブックでも何度か取り上げてきたテーマですが、循環小数は一見高校生にも馴染みのある素朴な存在です。しかし、その背後には大学数学の群論という、抽象でありながらも美しい理論が広がっています。
実は、群論の知識をひとたび手にすると、循環小数の見え方が劇的に変わり、より深い魅力に気づくことができるのです。題して
というわけです。
本記事では、巡回群や 、剰余群といった群論の用語が登場します。これらに少しでも触れたことがある方なら、より一層楽しんでいただけるでしょう。もちろん、群論に不慣れな方でも、循環小数という身近な題材を通じて「数学ってこんな風に深いんだ」と感じるきっかけになれば幸いです。
具体的には、
といった循環小数の計算例からスタートし、その魅力をひも解いていきます。
こういう図や

こういう図

が登場します。
ぜひ最後までご覧になってください。
目次:
0. 今回の記事で出てくる群論の基礎事項
本記事を読む上でおさえておきたい群論の基礎事項をいくつか紹介します。
この段階で理解する必要はないので、必要なときに戻ってきてください。
- 群の位数・元の位数
を群としたとき、
の要素数を群
の位数といい、
で表す
の元
について、
(単位元)となる最小の正の指数
を元
の位数という
- 巡回群
- 群
が
の元
を用いて
と表される
の部分群
を、
と表す。このとき、
は
で生成されるといい、
を
の生成元と呼ぶ。
となるような
が存在するとき、
は巡回群であるという。
- 群
1. 循環節の長さと群の位数(1/7を例に)
まず、基本的なところからおさらいしたいと思います。
が
や
以外の素因数を持つとき、
の小数展開は循環します。
たとえば、 とすると
となり、以降も が繰り返されます。
このように同じ並びが繰り返される単位のことを循環節といいます。

今回の記事を通して、 を素数として、
について考えたいと思います。
の循環節についていくつか例を挙げたいと思います(下線部が循環節です)。
(長さ1)
(長さ6)
(長さ2)
(長さ6)
(長さ16)
(長さ18)
(長さ22)
(長さ28)
(長さ15)
循環節の長さは分母の数によってまちまちです。
循環する桁数を考えるには、割り算の筆算を考えると分かりやすいです。

上の筆算は次の手順で計算されています:
- (小数第1位の計算)元の数
を
倍して
とし、これを
で割り算する(
あまり
を得る)。商の
を小数第1位とし、あまり
を次の桁の計算に用いる。
- (小数第2位の計算)あまり
を
倍して
とし、これを
で割り算する(
あまり
を得る)。商の
を小数第2位し、あまり
を次の桁の計算に用いる。
(以下、繰り返し)
小数第6位の計算結果にあまり が出ているのが注目ポイントです。
小数第7位の計算の際に、再び を実行することになり、以下、小数第1位と同じ結果が繰り返されます。したがって循環するというわけです。
以上の考察から、 が循環する仕組みは「
の筆算の計算の中で、あまりとして再び元の数
が登場すること」にあると分かります。
が登場するタイミングで循環節が終わることも同時に分かります。
ところで、筆算の途中過程をすっ飛ばすと、次のように見ることもできます:

これは、 を
で割ったあまりが
であることを意味します。
より一般に、 を
で割ったあまりが
であるときに、
は
桁で循環することになります。循環節の長さは、そのような
の中で最小のものとなります。
これは群論を使って言い換えることができます。
まず、
を考えます。
また、 の乗法群(逆元を持つ元全体のなす群)を
とします。
となります。
ここで、 の位数(べき乗して
になる最小の指数)が
の循環節の長さとなります。これは定義から明らかですね。
これらの関係を「循環小数の基本原則 *1」としてまとめておきましょう。
の循環節の長さ
「
を
で割ったあまりが
」である最小の素数
における
の位数
2. すべてのあまりを巡回する
の筆算を見ていると、もう少し面白いことが起きています。筆算の各桁を計算する際には、
を
で割ったあまりを順に計算することになります。
ここであまりの計算結果として のすべての元
が現れることがポイントです。

群論的には、 が生成する
の部分群が全体に一致することが分かります。すなわち
が成り立つということです。
が
で生成されることを図示するために、正七角形を用意してみました。

には
は入っていないので、一番上の
にバツ印をつけておきます。

からスタートして、頂点を繋いでいきます。

なので、
から
へと線を結びます。
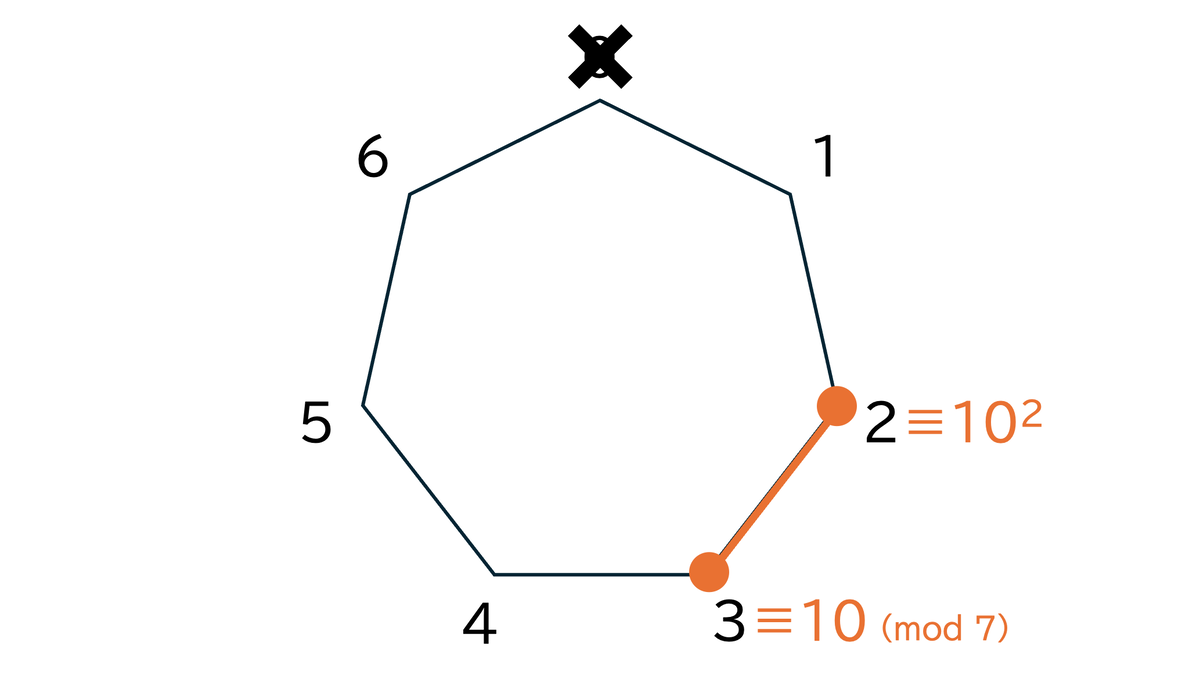
なので、
から
へと線を結びます。

と同様に繰り返して、次の図を得ます。

もう一度 を掛けると、
に一致するので、ぐるっと一周します。

これにて、 をひたすら掛けるだけで、
の元がすべて生成されることが確認できました。
一般に、 は巡回群です(ある1つの元
によって生成される)。これは数論的には原始根定理と呼ばれます。この定理は「体の乗法群の有限部分群が巡回群であること」から導かれます。
一方、原始根定理は生成元の存在だけが分かる定理なので、どのような元が生成元になるかは明らかではありません。
今回 のときに、たまたま
が生成元になりましたが、後で紹介する
のときは
は生成元にはなりません。
一般に、 が
の生成元であるときに限り、
の循環節の長さは
となります(「循環小数の基本原則」より)。
のとき、
が
の生成元であることから、
の循環節の長さが
となるわけです。
3. ダイヤル数が生まれる仕組み
上で述べた の循環節の長さが
であるという事実から、ダイヤル数 という興味深い性質が導かれます。
という「どこかで見たことある数」はダイヤル数と呼ばれる数の一種です(ダイヤル数の定義は後ほど)。
さて、この数に対して という数を掛けると、次のようになります:
このままでは少し分かりづらいので、順番を変えてみましょう:
色をつけるとより分かりやすくなります:
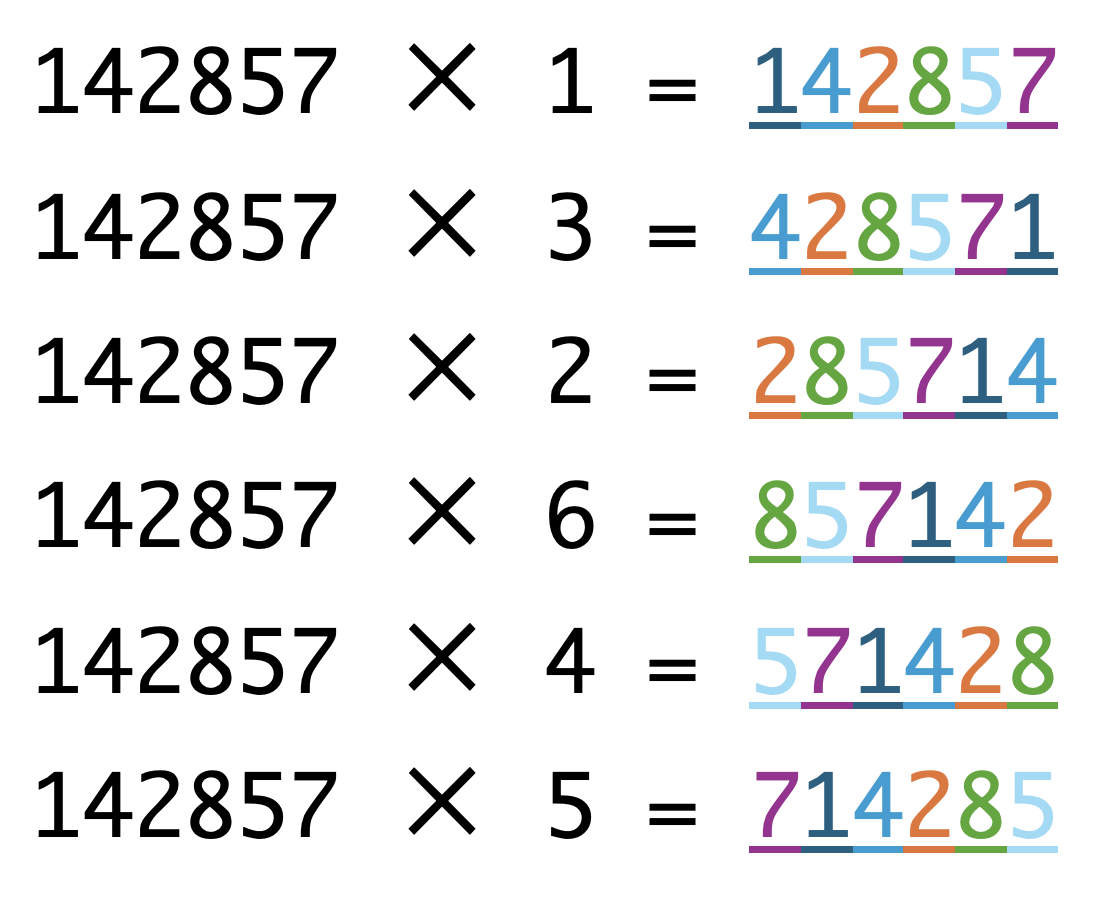
という数に、1 〜 6を掛けることによって1桁ずつ左にスライドしていることが分かります。面白いですね!
どうしてこんな現象が起きるのでしょうか。
わざとらしく「どこかで見たことある数」であると言いましたが、実は は
の循環節の数そのものですね。当然、「数を掛けると1桁ずつ左にスライドする」仕組みも
から導くことができます。
実際、上で紹介した左スライド現象は、 に1 〜 6の数を掛けることで再現されます:

問題は、なぜ に
を掛けることで循環節が左スライドするのか、という点ですが、このことは
の筆算と
の筆算を同時に見比べると分かります:

の筆算では
あまり
あまり
あまり
あまり
あまり
あまり
の計算が行われるわけですが、 の筆算では
あまり
が最初に計算されます。
つまり、 の計算では
において「あまり3が降ろされた桁(小数第2位)」から計算がスタートするのと同じことになります。だから小数展開の結果も、1個先の桁が登場することになるのです。
同様に の計算では、
において「あまり2が降ろされた桁(小数第3位)」から計算がスタートするのと同じことなので、小数点解の結果に2個先の桁が登場することになります。
以上が「数を掛けると1桁ずつ左にスライドする」仕組みです。
のときの
のような状況は、一般の素数
にも考えることができます。
の循環節の数を
としたとき、
が「
を巡回させた数」になるとき、
をダイヤル数といいます。
実は、
と、
は同値なのですが、このことはこれまでの議論をよくよく考えると分かります。以下で証明してみましょう。
「循環小数の基本原則」より②と
は同値なので、以下では①と③の同値性を示します。
(③ ① の証明)
の循環節を1桁左にスライドさせた小数は、
を
倍した数と等しくなります。同様に
桁左にスライドさせた数は
倍した数と等しくなります。

また、 の
倍した数の小数部分は、
である数
(
)に対する
と等しくなります。
(小数部分をとることは、分子を することに対応することに注意。)
したがって、集合としての等号
が成立するならば、 に対して
の循環節が
の循環節をスライドさせたものと(小数部分が)一致することになります(すなわち①が成立する)。
この等号が成立する条件は「③ 」と言い換えることができます。
したがって③が成立するならば、①が成立することが示されました。
(① ③ の証明)
対偶をとって「③ではない ①ではない」を考えます。
より、
を満たすような
(
)をとると
を満たす
が存在しません。
すなわち、この の循環節は、
の循環節をスライドさせた数になりません。
以上により「③ではない ①ではない」が示されました。
4. 剰余群から見る循環小数のクラス分け(1/13を例に)
ここまで の循環節がダイヤル数になる場合を考えてきましたが、ダイヤル数にならない場合はどうなるでしょうか。実はこの場合もとても面白いことが起きるのです。
として
の例を考えましょう。
ダイヤル数のときと同じように、 に
を掛けてみましょう。
このままだと分かりづらいので、2列に分けてみましょう。

色も付けてみると、より分かりやすくなります。

便宜上、左側を「 のクラス」、右側を「
のクラス」と呼ぶことにします。
は
を掛けると「
のクラス」の循環節に一致します。
(より強く「 のクラス」に属する循環小数に、
を掛けると「
のクラス」の循環節に一致します。)
一方で、 に
を掛けると、今度は「
のクラス」の循環節に一致します。
(より強く「 のクラス」に属する循環小数に、
を掛けると「
のクラス」の循環節に一致します。)
とても面白い現象ですが、裏にある背景を説明しましょう。
これを説明するためには の乗法群
が必要なので、
のときと同様、「正十三角形」を用意したいと思います。

上の頂点から時計回りに を配置します。

さて、 の筆算を計算して、登場するあまりを分析してみましょう。

図のように があまりとして出てきています。したがって、(
と同様に)
に
を掛けると
の循環節をスライドさせたものが得られることが分かります。
また、 は
を並べたものだと考えることができます。
つまり、群論的には
において、 が生成する部分群
を考えていることになります。
の元
を
に掛けると、「
のクラス」に属する循環小数ができるわけですね。
一方で、 の部分群
は、
の全体には一致しません。そのため、
を全てかけたときに、必ずしも「
のクラス」の循環小数は得られないということになります。つまり
はダイヤル数ではないというわけです。
の元ではない
を掛けたときはどのようになるのでしょうか。
の筆算を考えると分かります。
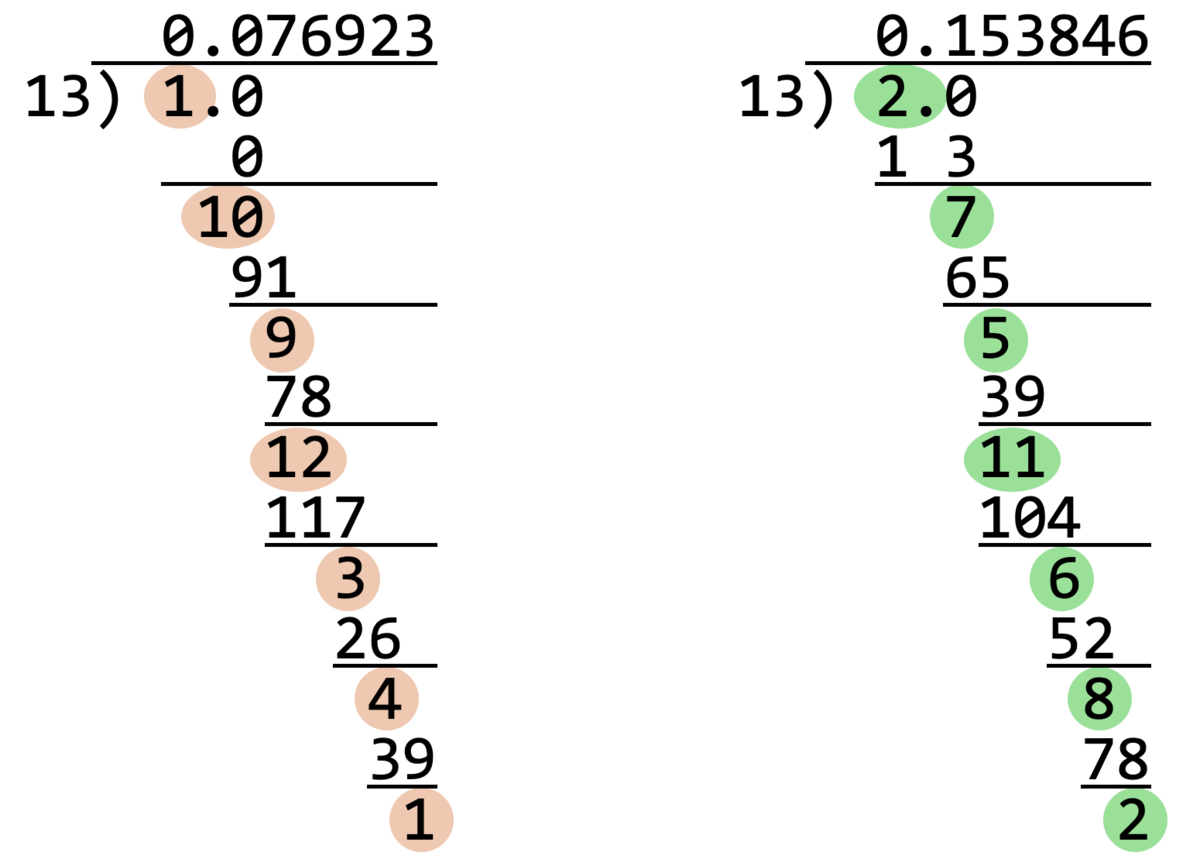
あまりに着目すると、 の筆算に出てくるあまりは
であり、ちょうど
から
を除いたものがすべて出てきています。

は
をちょうど2倍したものなので、
の筆算に出てくるあまりは、
の筆算に出てくるあまりのすべてを2倍して
とったものに等しくなります。

の筆算に出てくるあまりは
の元なので、これを
倍したものは
です。これは群論的には剰余類として捉えることができます。
つまり、群 の部分群
を考えて、
を
で割って得られる剰余群
の各剰余類 はそれぞれ「
のクラス」と「
のクラス」に対応していたというわけです。
(類は英語で "class" なので、まさに「クラス」という言い方がぴったりです。)
なお、剰余類の個数を の指数といい、
で表しますが、
が成り立つというのが、群論におけるラグランジュの定理でした。
今回の場合、、
、
であり、ラグランジュの定理はもちろん成り立っています。
循環小数側で考えると、 は循環節の長さで、
は循環小数のクラス分けの個数に対応するというわけです。群論の基本定理がこんなところにも現れるというのは面白いですね。
5. 他の循環小数ではどうなっているのか?
と
を例に議論してきましたが、もっと他の例も考えたくなりますね。
たとえば、
の場合を考えてみましょう。この場合の循環節の長さは でした。
を含む
という10個の循環小数を考えると、これらは循環節に出てくる数によって、5つのクラスに分類されます。

これもやはり群論によって説明できます。
の
が生成する部分群
に対して、 を
で割った剰余群
を考えればよいでしょう。剰余群の各剰余類が、上で挙げた循環小数の各クラスに対応しています。
の剰余類を図示すると次のようになります:
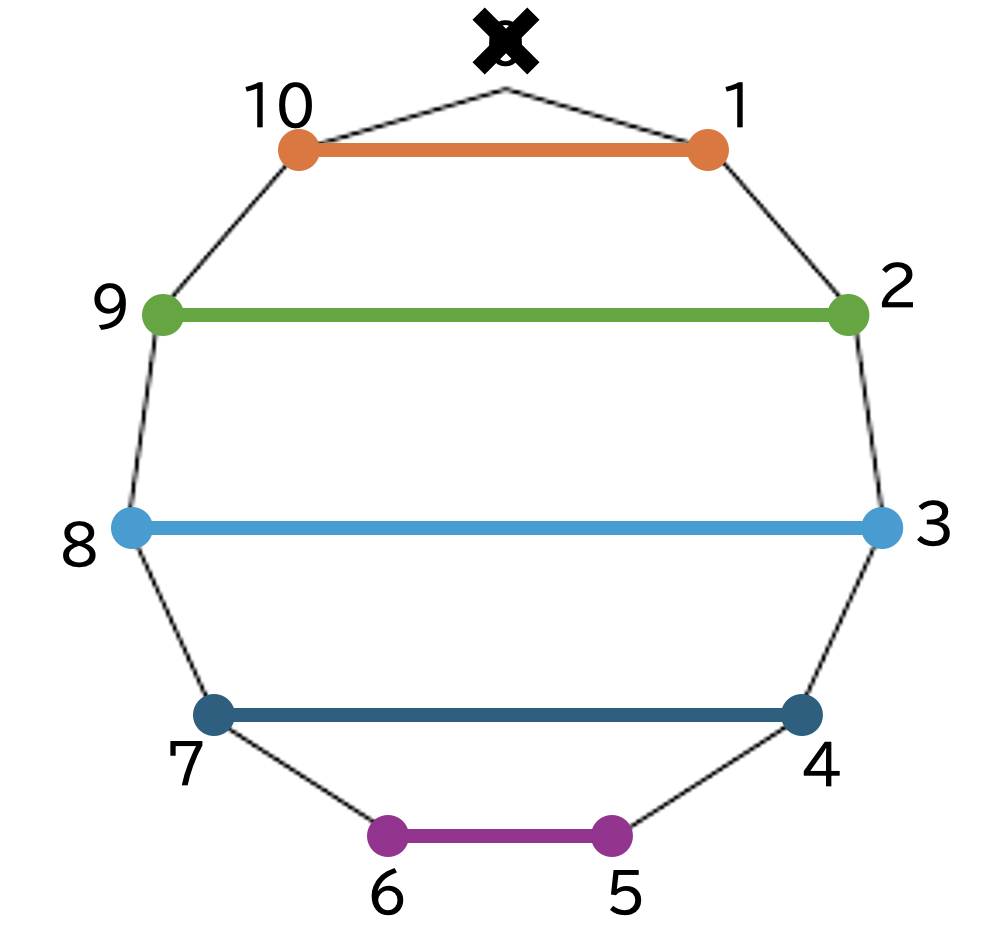
他にも、 なる素数
に対して、
の剰余群として
形循環小数のクラス分けを行うことができます。ぜひやってみてください。
6. まとめ
今回の記事では、一見単純に見える循環小数の世界に、群論という深遠な数学の視点から迫りました。
の例では、
の筆算に出てくるあまりにおいて
から
のすべてが登場するという事実が、
が
で生成されるという群論的な性質に対応することが分かりました。ここから自然に「
はダイヤル数」という性質が導かれるのでした。
また、 の例では、
の部分群とその剰余類に着目することで、
の循環節が自然にクラス分けされることが分かりました。
ラグランジュの定理をはじめとする群論の基本定理が、こうしたクラス分けの背景にある数学的な秩序を支えていることを実感できます。
そんなわけで、群論の視点を取り入れることで、循環小数に新しい見方を提供でき、とても面白いということが今回伝えたかったことです。楽しんでいただけましたでしょうか。
それでは今日はこの辺で!
*1:「循環小数の基本原則」という呼び方は、tsujimotterの独自のものなので、他では使わない方が無難です。