本記事は日曜数学 Advent Calendar 2024の1日目の記事です。
ご無沙汰しています。日曜数学者のtsujimotterです。
2024年も日曜数学アドベントカレンダーを立ち上げまして、今日の記事はその1日目の記事となります。
adventar.org
明日話したくなる数学豆知識 (2014)から数えると、なんと 11年目(素数) です。
おかげさまで既に全日25件が埋まっております。ありがたいことですね。記事が投稿されるのを楽しみにしています!
今日はバーコフのダイヤモンドの話がしたい
日曜数学アドベントカレンダーは、自分が好きなトピックについて熱く語るのが主旨です。
今日は、私の現在一番のお気に入り概念である
について、熱く語りたいと思います。
知り合ったきっかけは、YouTubeの下記動画を作るために、四色問題について勉強していたときでした。
www.youtube.com
バーコフのダイヤモンドとは、四色問題で扱われる地図の一部分を表す図形のことで、こんな形をしています。

「四色問題の最小の反例に出てこない配置」という大変魅力的な性質を持っています。
現時点ではなんのこっちゃ分からなくても、後々説明していきますのでご安心ください。
先走ってしまいましたが、まずは四色問題(四色定理)について順を追って説明したいと思います。
四色問題とは
四色問題は、地図の色の塗り分けに関する数学的な問題です。
「隣り合う国同士は異なる色で塗り分けるというルールで平面地図を塗ったときに、どんな平面地図であっても4色あれば塗り分けられることを証明せよ」
という問題です。

日本地図はもちろん4色で塗り分けられます。

「どんな平面地図であっても」とあるので、日本地図や世界地図などの現存する地図が塗り分けられたからよいというわけではないのがミソです。考え得るありとあらゆる地図 に対して4色で塗り分けられることを確認しないと、四色定理を証明できたことになりません。
現実のことを考えなければ、地図なんて無限に考えられるわけで、こんな問題をいったいどうやって証明するのだろうと思うのが自然です。
なんと四色問題は現在では解決しており、四色定理と呼ばれています。
1976年に、アッペルとハーケンと彼らの「助手」によって解決されました。
四色問題を提唱したのは1852年のガスリーなので、実に 124年間も未解決 だったことがわかります。相当な難問ですね。
この問題は単なる難問なだけでなく、物議をかもした問題でもあります。
実は四色定理の証明は、当時登場したばかりの コンピュータ によってなされた証明なのです。先ほど「助手」と書いたのは、コンピュータだったわけです。
現在でも、コンピュータを用いない四色定理の証明は実現されていません。四色定理の証明は「数学の証明は人間が行うものだ」という数学者の価値観を破壊するような証明でした。
もちろん、コンピュータを使ったからと言って、数学的な要素が全くないというわけでもありません。
コンピュータが得意なのは有限の範囲の探索なので、1個1個の地図を素朴に塗り分けるだけでは、いくら待ってもプログラムが停止しません。地図は無限にあるので。
無限にある地図の可能性を、いかにして有限の範囲に押し込んで議論できるようにするか。
そこに数学者の技量があったわけで、いったいどのようなアイデアがそこにあったのか興味が惹かれるところと思います。
その点を次の節で明らかにしていきましょう。
四色問題への4つのキーアイデア(前半)
四色問題はいかなる方法で解決されたのでしょうか。そこにバーコフのダイヤモンドを紐解くヒントがあります。
四色問題の証明に向けた、4つの重要なキーアイデアを紹介しましょう。
まず1つめのキーアイデアは、地図を グラフ で表すことです。
グラフとは、簡単に言ってしまえば点と線によって表された図形のことです。
「x軸y軸を引いて一次関数のグラフ〜」のようなグラフのことではありません。
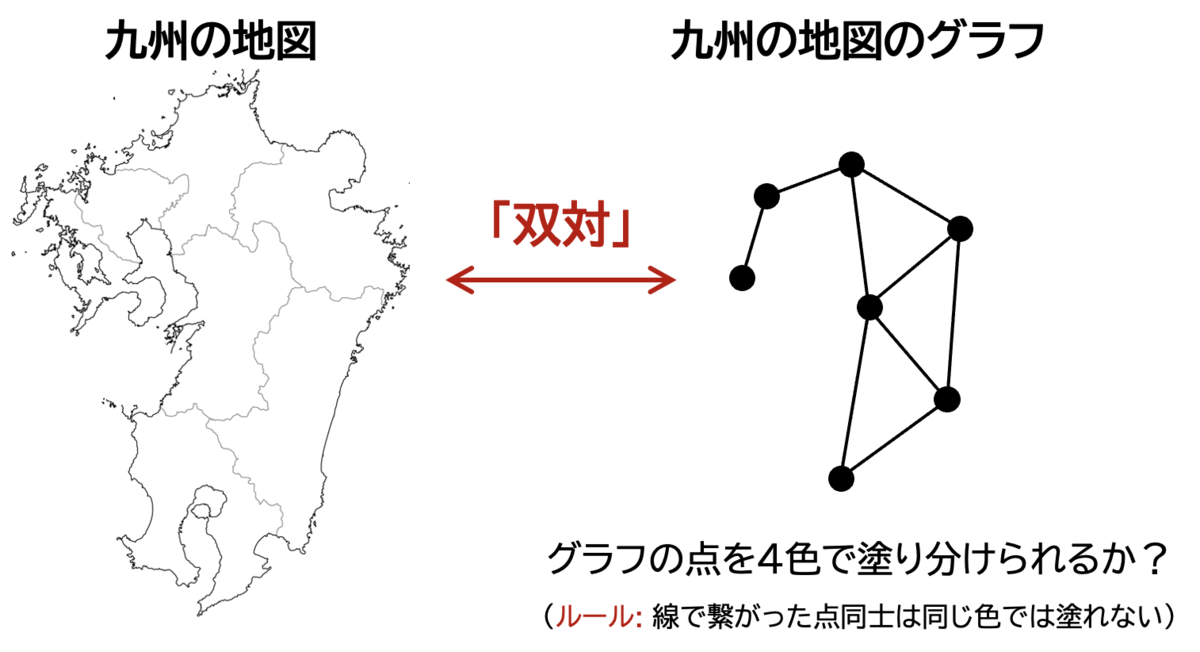
たとえば、以下の九州の地図は、各県の真ん中に点を置いて、隣接する県同士の点を結ぶというルールによって、グラフで表現できます。

これを地図のグラフということにしましょう。
四色問題は「線で結ばれた点同士は異なる色で塗り分けるというルールで地図のグラフの点を塗ったときに、どんな地図のグラフであっても4色あれば塗り分けられることを証明せよ」という問題に、言い換えることができます。
このようにすることで、純粋に国同士の隣接関係のみに注目することができるようになり、見通しがよくなります。
なお、地図と地図のグラフの関係は、双対 の関係にあるとも言われます。
グラフを扱う数学の分野を「グラフ理論」といいます。
グラフ理論においては、特に「次数」という概念が重要です。点の次数とは、その点に接続されている線の本数のことです。
たとえば、先ほどの九州のグラフにおいて、それぞれの点の次数は次の図のようになります:

熊本県は4つの県に隣接していますので、次数が4ということになります。
2つめのキーアイデアは、背理法 を使うことです。
背理法により「四色問題は成り立たない」と仮定します。すると、四色で塗れない地図が存在することになります。
これらはいくつかあるかもしれないですが、特に四色で塗れない「最小」の反例があるはずです。これを最小反例ということにしましょう。
ここでいう最小とは、地図のグラフにおける「点の数」と「線の数」の合計が最小であるということです。
最小反例より「点の数」と「線の数」の合計が小さい地図は、必ず4色で塗り分けられることが保証されている。そんな存在です。
四色問題への4つのキーアイデア(後半)
3つめと4つめのキーアイデアは、不可避集合 と 可約配置 を考えることなのですが、これらは素晴らしいアイデアです。
まとめて紹介しますが、定義は次の画像のとおりです:

画像に書いたとおり、もし仮に可約配置だけを要素に持つ不可避集合が作れたとすると、四色定理が証明できたことになります。実際、次のように証明できます。
まず、背理法により四色問題が誤りである、すなわち最小反例が存在すると仮定します。
最小反例というのは(定義より)可約配置を含みません。一方で、不可避集合の要素は必ず1つは含むはずですが、今考えている不可避集合の要素はすべて可約配置であるので、矛盾します。
したがって、反例が存在するという仮定が誤り、すなわち四色定理が証明できたことになります。
「可約配置だけを要素に持つ不可避集合」という有限の存在を作ることが四色定理の証明のキーというわけです。
不可避集合とは、どんな地図も必ず不可避集合を避けては通れない配置の集合ということになりますが、そんなもの作ることができるのでしょうか?
たとえば、次のような集合が不可避集合です。

実際、オイラーの多面体定理を用いると、任意の地図のグラフは次数5以下の点を必ず持つことが示せます。したがって、どんな地図であっても、上記の不可避集合の要素のいずれかは避けることができないというわけです。
こんなことに(「世界で二番目に美しい数式」で有名な)オイラーの多面体定理が使えるというのは驚きですし、結果も非自明で面白いですね。こんなふうに不可避集合を作ることができます。
しかしながら、上記の不可避集合では四色定理の証明はできません。
次数0〜4までは可約配置であることが示せます。
つまり、次数0〜4の点を が最小反例に含まれるとしましょう。このとき、点
を除いてできる地図は最小反例より小さい地図なので4色で塗り分けられます。
この状態で を戻したとき、次数0〜3の点の場合は周りの色と異なる色を塗れば良いですし、次数4の場合も周りをうまく塗り直すことで全体を4色で塗り分けることができます。
こんな具合で元の地図が4色で塗り分けられることが分かり、元の地図が反例であるという仮定に反します。
しかしながら、次数5の点に関しては、残念ながら可約ではありません。つまり、最小反例が次数5の点を含むとき、 を除く周りは4色で塗り分けられるわけですが、この状態で
を戻して再度4色で塗り直すということができないのです。

このような不可避集合によって四色問題の解決に挑んだのが ケンぺ という数学者です。彼自身は、本当にこの方法で四色定理を証明できたと思い込んでいたようです。
残念ながらその証明(次数5が可約配置であることの証明)が誤りであることが後の数学者によって明らかになり、ケンぺの試みは失敗に終わりました。
そんなわけでケンぺの不可避集合では失敗したわけですが、すべての要素が可約配置であるような不可避集合が見つかりさえすれば四色定理が証明できます。実際、そんなうまい不可避集合を見つけることができるのでしょうか。
改めてバーコフのダイヤモンドとは
キーアイデア3と4を改めて再掲します。

私はこのアイデアを聞いたとき、感動しました。なるほど、こんな天才的な方法で、無限に思える四色問題を有限に押し込めることができるのかと。
実は上記の枠組みによって四色定理を証明できることを最初に提示したのが バーコフ という数学者です。
そしてそのバーコフが見つけた、(次数0〜4の点以外の)最初の可約配置が バーコフのダイヤモンド というわけです。
改めてバーコフのダイヤモンドを見てみましょう。

左側が地図上の形を表していて、右側がその地図のグラフを表しています。これらは双対の関係にあります。
バーコフのダイヤモンドは次数5の点が4つ組み合わさって構成されています。実際には地図の中に配置されているわけですが、周囲には6つの点と接しています。

バーコフのダイヤモンドは可約配置なので、つまりこの配置は最小反例には含まれないということです。
これがとても重要な性質なわけですが、これを示すためにはバーコフのダイヤモンドが最小反例に含まれると仮定して矛盾を導く必要があります。
実際、最小反例に含まれると仮定すると、それより小さな地図は4色で塗り分けられることが保証されるわけです。
そこで、バーコフのダイヤモンドの部分を除いて、より小さな地図(下の図の右)を作ります。すると、4色で塗り分けることができます。

バーコフのダイヤモンドを元の地図に戻して、改めてバーコフのダイヤモンドの部分を4色で塗り分けられるか検討します。
実際には、バーコフのダイヤモンドの部分以外の部分も改めて塗り直す必要があり、塗り直して4色で塗り分けられることが示せます。
したがって、バーコフのダイヤモンドを含む最小反例が、実は4色で塗り分けられてしまったということが示されます(矛盾)。このことより、バーコフのダイヤモンドが最小反例には含まれない(可約配置であること)が証明されると言う寸法です。
しかしながら、ここで完全な証明をするためにはやや込み入った話になってしまいますので、またいつか別の記事で紹介したいと思います。
ここで伝えたいのは、バーコフのダイヤモンドは最初に見つかった非自明な可約配置であるということです。
実は四色定理の証明にも登場するバーコフのダイヤモンド
バーコフのダイヤモンドは、四色定理の証明に向けたアプローチの中で証明された最初の可約配置というわけですが、実は最終的な四色定理の証明にも関わっています。
最終的に、1976年のアッペルとハーケンによって構成されたものは、1936個 の可約配置からなる不可避集合でした。とんでもない数ですね。
このような不可避集合を探索するのに、そしてそれぞれが可約であることを示すのにコンピュータが用いられました。
最終的に得られたリストは、アッペルとハーケンの論文2報のうち、2報目の "Every planar map is four colorable. Part II: Reducibility" に図として掲載されています。

今回、特に強調したいのが、この左上の図こそがバーコフのダイヤモンドだという点です。
つまり、最終的に四色問題の解決に用いられたアッペルとハーケンの不可避集合のリストに、バーコフのダイヤモンドが載っているというのです。
しかも実はリストの1番目です。
アッペルとハーケンの「バーコフのダイヤモンドへの敬意」が感じ取れる気がするのは、私だけでしょうか。笑
まとめると、バーコフのダイヤモンドは四色問題へのアプローチの提唱時に登場したというだけではなく、四色問題の解決にも一役買っているということですね。
バーコフのダイヤモンドすごい!!!!!
バーコフのダイヤモンドリングを作ってみた
そんなわけで、四色問題の勉強をしていくうちに、バーコフのダイヤモンドという超絶面白概念と出会うことができました。
ところで、ダイヤモンドと言って僕の頭に浮かぶものといえば、ダイヤモンドリング です。
考えてみると、地図のグラフにおける 「双対」 のイメージはペアリングにぴったりかも。
そんなアイデアを妻に話したところ、「ダイヤモンドの無いダイヤモンドリング、おもしろい!」とノリノリ。なるほど、それは面白いぞ!
そんなわけで、バーコフのダイヤモンドリングを作ってみました!!!

ネットで検索をしまして、家から通える範囲にあった「ケイウノ」さんに相談にいくことに。
デザイナーさんに我々夫婦の希望や、四色定理やバーコフのダイヤモンドへの愛を伝えると、デザイナーさんがその場でデザインを描いてくれました。

なにこれめっちゃかっこいいんだが!!!
バーコフのダイヤモンドのモチーフを入れつつ、指輪としても成立するデザインにまとめ上げてくれました。ちゃんと、夫婦で双対(ペアリング)になっています。
ここから一ヶ月程度かけて製作いただきまして、先日実物の指輪が届きました!
それがこちらです!!!

いやー、ほんと感激ですね。まさかほんとにバーコフのダイヤモンドがダイヤモンドリングになってしまうなんて。
お気に入りの概念と共に過ごす日々は格別だと思います。
これからは四色問題の歴史の重みを毎日感じながら過ごすことができそうです。
(日々の過ごし方それでいいのか?)
最後に、デザイン画と一緒にパシャリ。

最後まで読んでくださってありがとうございます!
それでは今日はこの辺で!!

