カタラン予想とマチンの公式 - tsujimotterのノートブック

カタラン予想は、次のような有名な数論の予想です。

$X^u - Y^v = 1 \tag{1}$

を満たす正の整数 $X, \; Y, \; u > 1, \; v > 1$ の組は $(X, Y, u, v) = (3, 2, 2, 3)$ に限る．

「予想」とはいっても、実はもう既に解決されている問題です。

カタラン予想は、2002年にミハイレスクという数学者によって解決されました。このことについては、以前のブログ記事でも紹介したことがありました。

さて、今日お話したいのは

カタラン予想に「円周率の公式」が関係している

というお話です。円周率の公式に「マチンの公式」と呼ばれるものがあり、マチンの公式に関連する研究成果が、カタラン予想の部分的な問題の解決に貢献しているというのです。非常に興味深いお話なので、このブログの読者にも気に入ってもらえるのではないかと思います。

実は、今回のテーマについては、１月２７日に開催の「関西日曜数学友の会」というイベントで、Tomohiro Yamada さんが発表されるそうです。tsujimotter もこのイベントや Yamada さんの発表をとても楽しみにしているのですが、実は自分としても思い入れのある話であり *1、今日はこのテーマで書かせていただきます。

イベントに参加される方は、ネタバレを含む可能性もありますので、ぜひそちらの講演を楽しみにしていただければと思います。

1. カタラン予想の歴史

カタラン予想は、1844年に問題提起されてから、ミハイレスクによって2002年に解決されるまで、実に 158 年を要した数論の難問の一つでした。

150年以上もの間、何も進展がなかったかというと、そうではありません。数多くの数学者によって、カタラン予想は挑まれていたのです。

数学者たちとった戦略は、変数を固定して問題を簡単化するということでした。

たとえば、オイラーによって、 $u = 2, v = 3$ を固定した問題

$X^2 - Y^3 = 1$

については解決されています。

オイラーによって変数２つを固定した問題が解決されたわけですが、その後の研究者によって、 $u, v$ のいずれか一方だけを固定した問題が取り組まれるようになりました。

主に研究されたのが

$X^u - Y^2 = 1 \tag{2}$

$X^2 - Y^v = 1 \tag{3}$

という形の方程式です。

一見すると、どちらも似たような問題に見えますが、実際は難易度がまったく異なります。

みなさんは、どちらの方が難しいと思いますか？

＊　＊　＊　少し考えてみてください　＊　＊　＊

正解は「下の方が難しい」です。

上の問題 $X^u - Y^2 = 1$ は、Lebesgue *2 によって1850年に解決されています。この結果は、後でまた登場しますので覚えていてください。

一方で、下の問題 $X^2 - Y^v = 1$ はそう簡単ではありませんでした。実際、100年以上経った1960年・1964年の Chao Ko の研究まで未解決だったようです。

今回の記事では、 $X^2 - Y^v = 1$ に対する挑戦の過程で得られた、Selberg *3 による結果を紹介したいと思います。Selberg によって、 $X^2 - Y^v = 1$ の問題が次のように部分的に解決されました *4。

本日の主定理（Selberg, 1932）

$v \geq 2$ のとき，方程式

$X^4 - Y^v = 1 \tag{4}$

の整数解は，自明な解（ $X = \pm 1, Y = 0$ ）しか存在しない．

移項させると $X^4 = Y^v + 1$ となりますから「 $Y^v + 1$ という形の数は 4 乗数にはなりえない」という風に解釈できますね。

Selberg の定理の証明には、Størmer という数学者の研究結果が用いられました。関連するのは 1899 年に発表された次の論文です。

Solution complete en nombres entiers de l'equation $m \arctan \frac{1}{x} + n \arctan \frac{1}{y} = k\frac{\pi}{4}$

フランス語で書かれた論文ですが、なんとなくタイトルはわかりますね。日本語訳すると

方程式 $m \arctan \frac{1}{x} + n \arctan \frac{1}{y} = k\frac{\pi}{4}$ の整数における完全な解

という感じになるでしょうか。

あれ？ぜんぜんカタラン予想っぽくない・・・

と思いませんでしたか。

ところがどっこい、これがカタラン予想と密接に繋がってくるのです。

2. 円周率を計算する Machin-like formula

Størmer が研究していたのは、カタラン予想ではなく「円周率の公式」についてでした。

円周率にはマチンの公式と呼ばれるよく知られた公式があります。

$\displaystyle 4\arctan \frac{1}{5} - \arctan \frac{1}{239} = \frac{\pi}{4} \tag{5}$

マチンの公式の左辺の $\arctan$ を展開することで、非常に速く収束する級数を作ることが出来ます。この公式によって「円周率の計算が大幅に改善した」というお話は有名かと思います。

マチンの公式に類する公式はほかにも知られていて、総称して Machin-like formula と呼ばれています。たとえば、こんな式も成り立ちます。

$\displaystyle \arctan \frac{1}{2} + \arctan \frac{1}{3} = \frac{\pi}{4}$

$\displaystyle 2\arctan \frac{1}{2} - \arctan \frac{1}{7} = \frac{\pi}{4}$

$\displaystyle 2\arctan \frac{1}{3} + \arctan \frac{1}{7} = \frac{\pi}{4}$

以上の式の $\arctan$ の項数は 2 つだけですが、もっと多くの項を扱った公式も知られていて、それらも Machin-like formula と呼ばれています。

参考：
Machin-like formula - Wikipedia

先ほどの Størmer の結果は、Machin-like formula についての研究でした。特に

$\displaystyle m \arctan \frac{1}{x} + n \arctan \frac{1}{y} = k\frac{\pi}{4} \tag{6}$

という形のものに対して、Machin-like formula をすべて求めようとしたのです。

3. Gravé の問題の解析

「式 $(6)$ の形の式をすべて求めよ」という問題は、Gravé の問題と呼ばれています。Størmer 以前に Gravé という数学者によって研究されていたそうです。

Størmer のすごいところは、Gravé の問題を完全解決したことです。

Gravé の問題を整理すると、以下のようになります。

Gravé の問題

$\displaystyle m \arctan \frac{1}{x} + n \arctan \frac{1}{y} = k\frac{\pi}{4} \tag{6再掲}$

を満たす $0$ でない整数 $m, n, k, x, y$ （ただし， $k, x, y \geq 1$ ）をすべて列挙せよ

ここで、整数 $m, n$ は互いに素と仮定しても一般性を失わないことに注意します。

Gravé の問題を理解するための第一歩は、図形的に考えることです。まずは、例題として

$\displaystyle 2\arctan{\frac{1}{3}} + \arctan{\frac{1}{7}} = \frac{\pi}{4}$

という式を分析してみましょう。

まず、 $\arctan$ の定義より、底辺 $x$ 高さ $1$ の直角三角形の角は $\arctan{\frac{1}{x}}$ と表せます。

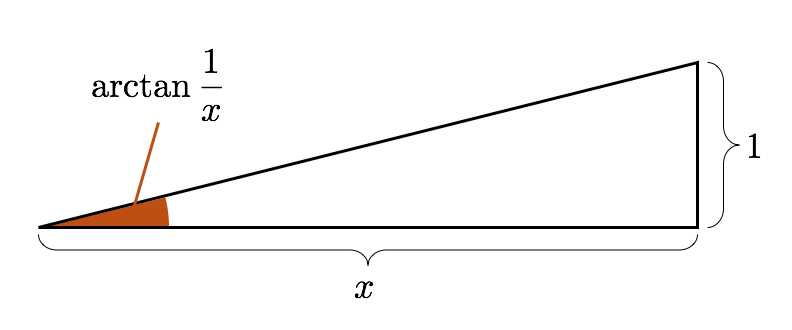
したがって、左辺の最初の項 $2\arctan{\frac{1}{3}}$ は、底辺 $3$ 高さ $1$ の直角三角形を考えて、そのなす角の 2 倍ということになります。

次に、この直角三角形を複素数平面上で考えます。先の直角三角形は、複素数 $3 + i$ で表せます。この複素数に対して、２乗 $(3 + i)^2$ を考えると、実軸とのなす角はド・モルガンの定理より 2 倍になります。したがって、 $(3+i)^2$ のなす角が $2\arctan{\frac{1}{3}}$ となります。

同様に $7 + i$ を考えると、そのなす角が $\arctan{\frac{1}{7}}$ となります。

したがって、これらの角を足し合わせると左辺に一致します。これはつまり、複素数 $(3+i)^2, (7+i)$ の積を取ることに相当します。 $(3+i)^2 (7+i)$ をプロットしたのが次の図です。

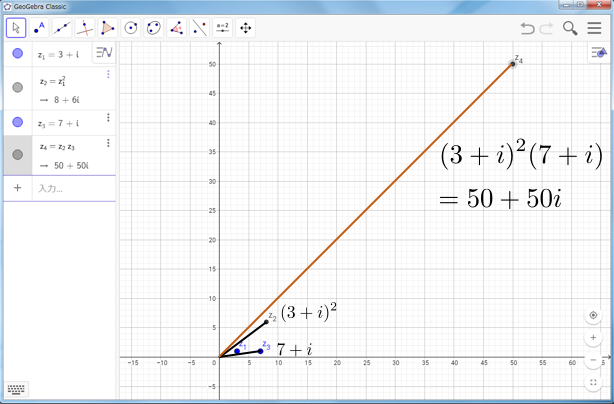
すると

$(3+i)^2 (7+i) = 50 + 50i$

となり、得られた複素数のなす角は $\frac{\pi}{4}$ に一致しますので、両辺が一致することが確認できるというわけです。

一般化に備えて少し見方を変えましょう。得られた複素数 $50 + 50i$ に $1 - i$ を掛けてあげれば、 $-\frac{\pi}{4}$ 回転させて実軸に戻ります。よって、 $(1-i)(3+i)^2 (7+i)$ が実数である、ということを確かめれば Gravé の問題の解であることが確認できます。

さて、一般のケースに話を戻しましょう。以上の議論を一般化すると、Gravé の問題における式 $(4)$ を満たす整数 $x, y, m, n, k$ は

$(1 - i)^k(x + i)^m(y + i)^n$ は実数

という条件を満たすとわかります。

あとは、この条件に合致する整数の組を列挙すればよいわけですね。

さて、次に思い出してもらいたいのは「複素数 $z$ が実数である」という条件の考え方です。高校数学でも習う以下の基本的な事実を使います。

$z$ が実数　 $\Longleftrightarrow$ 　 $\overline{z} = z$

「複素共役が元の数と等しければ、その数は実数である」ということですね *5。

複素共役を考えると

$(1 - i)^k(x + i)^m(y + i)^n = (1 + i)^k(x - i)^m(y - i)^n \tag{7}$

という式が得られます。ずいぶんと扱いやすそうな形に変形されました。

4. Størmer の定理に帰着させる

この節では、式 $(7)$ の条件をさらに変形し、「Størmer の定理」 に帰着させたいと思います。Størmer は、ある方程式の整数解を求める問題に帰着させ、その問題を解決することで（これが Størmer の定理）Gravé の問題を解いたのです。

以下では、 $\mathbb{Z}[i]$ における整数論を用いた「技術的に難しい議論」が続きます。難しいなと感じたらこの節の議論は飛ばして、最終的な結果である「Størmer の定理」を読んで、次の節に進んでみてください。

まず

$\begin{align} x + i &= (1+i)^\nu (a + ib) \\ y + i &= (1+i)^\mu (c + id) \end{align} \tag{8}$

とおきます。

$(1+i)$ をかけて回転させると $x + i$ に一致するような $a + ib$ を考えるということです。 $y + i$ も同様です。

ここで、 $\nu = 0$ または $\nu = 1$ としておきます。 $\mu$ も同様です。

$\nu$ が $1$ 以下である理由は、それぞれの式の共役をとってみるとわかります。

$\begin{align} 1 + x^2 &= 2^\nu (a^2 + b^2) \\ 1 + y^2 &= 2^\mu (c^2 + d^2) \end{align}$

ここで、左辺の $1 + x^2$ を $\bmod{4}$ で考えると

$1 + 0^2 \equiv 1$

$1 + 1^2 \equiv 2$

$1 + 2^2 \equiv 1$

$1 + 3^2 \equiv 2$

となって、4 で割り切れないことがわかります。したがって、 $1+x^2$ は 2 で「最大 1 回」しか割り切れませんので、 $\nu = 0$ または $\nu = 1$ となるわけです。 $1 + x^2$ が偶数になれば $\nu = 1$ となり、奇数になれば $\nu = 0$ となります。

また、最大１回分の $(1+i)$ はすべて $(1+i)^\nu$ が請け負うので、 $a + ib, c + id$ は $1 + i$ で割り切れないとすることができます。

式 $(8)$ を式 $(7)$ の条件に代入すると

$\mathrm{l.h.s \; of \;} (7) = (1-i)^k (1+i)^{m\nu} (a+ib)^{m} (1+i)^{n\mu}(c+id)^n$

$\mathrm{r.h.s \; of \;} (7) = (1+i)^k (1-i)^{m\nu} (a-ib)^{m} (1-i)^{n\mu}(c-id)^n$

となり、 $1 + i = i(1 - i)$ を考慮して $(1+i), (1-i)$ を消去すると

$(a + ib)^m (c + id)^n = i^\rho (a - ib)^m (c - id)^n$

が得られます。

両辺を見比べると、 $(a + ib)$ と $(a - ib)$ は互いに素なので、単数 $\varepsilon$ を用いて

$(a + ib)^m = \varepsilon (c - id)^n$

となります。

また、 $m, n$ は互いに素なので、 $a + ib$ は $\mathbb{Z}[i]$ の $n$ 乗数に単数をかけたものになります。 $c + id$ も $\mathbb{Z}[i]$ の $m$ 乗数に単数をかけたものになります。したがって、共通の $\mathbb{Z}[i]$ の元 $\alpha + i \beta$ を用いて

$\begin{align} a + ib &= \varepsilon_1 (\alpha + i \beta)^n \\ c - id &= \varepsilon_2 (\alpha + i \beta)^m \end{align}$

と表せることになります。

これを式 $(8)$ に代入すると

$\begin{align} x + i &= \varepsilon_1 (1+i)^\nu (\alpha + i \beta)^n \\ y + i &= \varepsilon_2 (1+i)^\mu (\alpha - i \beta)^m \end{align} \tag{9}$

が得られます。

両式の複素共役をとって、それぞれ元の式と掛け合わせると

$\begin{align} 1 + x^2 &= 2^\nu (\alpha ^2+ \beta^2)^n \\ 1 + y^2 &= 2^\mu (\alpha^2 + \beta^2)^m \end{align} \tag{10}$

が得られます。

$A = \alpha^2 + \beta^2$ とおくと以下の条件が得られます。

$\begin{align} 1 + x^2 &= 2^\nu A^n \\ 1 + y^2 &= 2^\mu A^m \\ x + y &\equiv 0 \pmod{A} \end{align}$

今回の話ではあまり本質的ではないのですが、最後の合同条件は以下のように得られます。

まず、式 $(10)$ に $A = \alpha^2 + \beta^2$ と置いた上で両式を引き算すると

$(1 + x^2) - (1 + y^2) = 2^\nu A^n - 2^\mu A^m$

となりますが、右辺は $A$ で割り切れます。左辺は $x^2 - y^2 = (x - y)(x + y)$ と因数分解出来ますが、 $(x - y)$ は式 $(9)$ の引き算より

$x - y = \varepsilon_1 (1+i)^\nu (\alpha + i \beta)^n - \varepsilon_2 (1+i)^\mu (\alpha - i \beta)^m$

となり、 $A$ では割り切れません。よって $x + y$ が $A$ で割り切れることになります。

以上の議論により、問題は

$1 + X^2 = Z^n \tag{11}$

$1 + X^2 = 2Z^n \tag{12}$

という形の方程式の整数解を求める問題に帰着されました。長かったですが、これが得たかった結論です。

式 $(11)$ は移行すると

$Z^n - X^2 = 1$

という形の方程式になり、これは冒頭で述べた Lebesgue の定理が適用できます。したがって、式 $(11)$ には自明な解 $Z = \pm 1, X = 0$ しか存在しません。

残りは式 $(12)$ です。これについては、Størmer が次の重要な結果を示しています。

定理（Størmer, 1897）

$n > 1$ が $2$ のべき乗でないとき，

$1 + X^2 = 2Z^n$

の解は $(X, Z) = (\pm 1, \pm 1)$ のみである．

※ 2017.12.29 訂正：「定理（Størmer, 1899）」と記載していましたが、実際に Størmer がこの結果を示したのは 1897 年の論文だったそうです。訂正させていただきます。

Størmer の定理こそが、今回のお話の最大のキーとなる定理です。

この定理と $n$ が $2$ のべきのケースを考えると、Gravé の問題が完全に解決することがわかります。たとえば、 $n = 4$ のときには

$1 + X^2 = 2Z^4$

が解 $(X, Z) = (\pm 239, \pm 13)$ を持つことが示されています。（これはStørmerの後、Ljunggren（1942）で示された結果です。）

ここからマチンの公式

$\displaystyle 4\arctan \frac{1}{5} - \arctan \frac{1}{239} = \frac{\pi}{4} \tag{5再掲}$

も得られます。

以上の結果によって、Gravé の問題の解は、上の具体例で述べた Machin-like formula ですべてだとわかるのです。すごいですね！

5. Selbergの定理の証明

ここまでMachin-like-formulaの話をしてきましたが、いよいよ本題のカタラン予想の話をしたいと思います。ずいぶん長い道のりを経てきたので、もう一度 Selberg の定理の主張を思い出しておきます。

本日の主定理（Selberg, 1932）（再掲）

$v \geq 2$ のとき，方程式

$X^4 - Y^v = 1 \tag{4再掲}$

の整数解は，自明な解（ $X = \pm 1, Y = 0$ ）しか存在しない．

$n$ が奇数のときの Størmer の定理を使うことで、Selberg の定理、すなわちカタラン予想の部分的な解決ができるのです。やってみましょう。

（証明）
$v$ が偶数のケースと奇数のケースで場合分けします。

$(i)$ まず、 $v$ が偶数のケースを考える。 $v$ は偶数より、 $v = 2m$ とおきます。

すると

$X^4 - Y^{2m} = (X^2 - Y^m)(X^2 + Y^m) = 1$

となります。掛けて $1$ になる２つの整数の組は、 $(1, 1)$ か $(-1, -1)$ の２組だけです。いずれのケースからも

$X^2 - Y^m = X^2 + Y^m$

が得られます。したがって $Y = 0$ がわかり、元の式に代入すると $X = \pm 1$ が得られます。したがって、 $v$ が偶数のときは、自明な解しか得られないことがわかりました。

$(ii)$ 次に、 $v$ が奇数のケースを考えます。さらに、 $Y$ が偶数と奇数で場合分けします。

$(a)$ $Y$ が奇数のとき：

$Y^n = X^4 - 1 = (X^2 + 1)(X^2 - 1)$

とかけます。 $X^2 + 1, X^2 - 1$ は「差が $2$ である整数組」なので、 $3$ 以上の共通の素因数を持ちません。一方で、左辺の $Y$ は奇数より、 $2$ も共通の素因数として持たないことがわかります。したがって、 $X^2 + 1, X^2 - 1$ は互いに素です。

よって

$X^2 + 1 = a^n$

$X^2 - 1 = b^n$

なる自然数 $a, b$ が存在します。一方で、差をとると $a^n - b^n = 2$ となって、これを満たすような $a, b$ は存在しません *6。したがって、 $Y$ が奇数のときは解が存在しないことがわかります。

$(b)$ $Y$ が偶数のとき：
$\bmod{4}$ で考えると、 $X^2 + 1, X^2 - 1$ はそれぞれ

$0^2 + 1 \equiv 1$ かつ $0^2 - 1 \equiv 3$
$1^2 + 1 \equiv 2$ かつ $1^2 - 1 \equiv 0$
$2^2 + 1 \equiv 1$ かつ $2^2 - 1 \equiv 3$
$3^2 + 1 \equiv 2$ かつ $3^2 - 1 \equiv 0$

のいずれかとなります。

ここで、 $Y$ は偶数より、 $Y^n$ の因数である $2^n$ を $X^2 + 1, X^2 - 1$ に分け与えることになります。 $X \equiv 0, 2$ のときは、 $X^2 + 1, X^2 - 1$ のどちらも $2$ で割り切れず不合理です。したがって、 $X \equiv 1, 3$ のケース、すなわち

$X^2 + 1$ がちょうど 1 回 $2$ で割り切れて
$X^2 - 1$ が $2^{n-1}$ で割り切れる

ケースを考えれば良いとわかります。したがって

$X^2 + 1 = 2a^n$

$X^2 - 1 = 2^{n-1}b^n$

とおくことができます。

ここで Størmer の定理より

$1 + X^2 = 2a^n$

は、 $n > 1$ が奇数のときには自明な解しかもたないとわかるので、 $X = \pm 1$ が得られます。 $X = \pm 1$ を $Y^n = X^4 - 1$ に代入すると、 $Y = 0$ が得られます。

したがって、 $v$ が奇数のときも、自明な解しか得られないことがわかりました。

以上の議論から、すべてのケースにおいて、 $X^4 - Y^n = 1$ は自明な解しかもたないことが示されました。

（証明終わり）

まとめ

今日は、円周率の公式を求めるための Størmer の結果が、カタラン予想の Selberg の結果に使われる、というお話を紹介しました。異なる分野が結びつくというのは、数学の醍醐味の一つで、魅力的だなと常々思っています。今回もまさにそのようなお話でした。

まとめとして、今回登場したキーワードの関連性を図でまとめてみましょう。

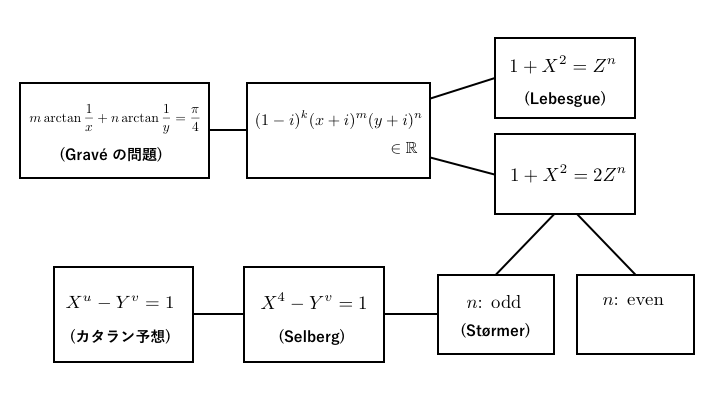
私自身は、これまで「マチンの公式」自体は知っていたものの、その意義をよく理解しておりませんでした。単に計算上便利なだけで、数学的に面白いものではないだろうと（勝手に）思い込んでいたのですが、このような形で数論の重要な問題に関連しているというのは本当に衝撃的でした。調べてみてよかったなと思いました。

読んでくださった皆さま、ありがとうございました。

それでは、今日はこの辺で。

参考文献

Størmer (1899) の論文です。フランス語の文献で苦戦しましたが、Google 翻訳に助けらながら読み進めました。今回紹介したのは、主に第２章の後半です。第４章では、Machin-like formula をすべて導出しています。

Solution complète en nombres entiers de l’équation $m\arctan \frac{1}{x}+n\arctan \frac{1}{y}=k\frac{\pi }{4}$

今回のテーマは、リーベンボイム先生のこちらの本で知りました。該当箇所は「７章　連続する巾乗数」です。

我が数、我が友よ: 数論への招待

作者:パウロリーベンボイム
共立出版

Amazon

難しいですが、非常に面白い内容に富んだ本で、tsujmotter のお気に入りの本です。まるで「行きつけの寿司屋」みたいに「簡単には人にお勧めしたくないな」と思ってしまうくらいお気に入りの本です。

時々誤植があるので、じっくり読む際は気をつけてください。

*1:実を言うと、tsujimotterも来年の日曜数学会で発表しようと思って、ちょうど勉強していたテーマでした。 12/12 ごろリーベンボイム先生の本をパラパラめくっていてこのテーマに出会ったのですが、読めば読むほど面白くて、その日のうちに真剣に取り組もうと決めたのです。本では詳細まで立ち入っていなかったので、Størmer の結果を理解するために慣れないフランス語の論文に挑戦したりもしました。そんな折、つい先日のインテジャーズアドベントカレンダー25日目の記事で、 Tomohiro Yamada さんがほぼ同様のテーマで発表されるということを知りました。なかなか日本語の文献のないテーマなので、知っている人はいないだろうと思っていたので、発表テーマが被ってしまったのには非常に驚きました。とはいえ、自分なりには結構しっかり勉強したので、Yamadaさんの発表を聞いて今回の内容を知ったと思われてしまうのは少し悲しいという気持ちもあり。また、自分が面白いと思って勉強したことをこのまま封印してしまうのも勿体無いと思い、どうしても公開したいと思ってこのような形とさせていただきました。

*2:ルベーグ積分の人とは別人です

*3:有名なアトル・セルバーグとは別人です

*4:Selberg の結果は「 $X$ が平方数」という条件においては $X^2 - Y^v = 1$ の問題を解決していると見ることができて、この意味で部分的な解決となっています。