一昨日にこんなツイートをしてみたら、思った以上に多くの方に面白がってもらえました。せっかくなので、この記事を通して「種明かし(?)」をしたいと思います。
√pの作り方 pic.twitter.com/qy2gzay6EW
— tsujimotter (@tsujimotter) 2020年3月31日
今回は3日連続で投稿する「ガウス和シリーズ」の第1回の記事となっています。よかったら続きもぜひご覧になってください:
tsujimotter.hatenablog.com
平方剰余/平方非剰余
今回の記事全体を通して、 を奇数の素数とします。
で割り切れない整数
に対して、次のような合同式を考えます:
解 が整数の範囲に存在するとき、
は
の平方剰余といいます。逆に、そうでないとき
は
の平方非剰余といいます。
このことを記号であらわすために、 は
の平方剰余のとき
は
の平方非剰余のとき
と表すことにします。
(これは平方剰余を表す形式的な記号であって、 に分数としての意味はないことに注意。)
たとえば、 のとき
が成り立つので、 は
の平方剰余です。逆に
を満たす整数 は存在しないため、
は
の平方非剰余です。
上の記号を使って表すと
ということになりますね。
整数論においてこの平方剰余はたいへん重要視されていて、とても興味深い性質がたくさん調べられています。
その一つが、今回のネタである 「ガウス和」 という量の持つ次の性質です。
ガウス和とその性質
ガウス和は、平方剰余の記号を用いて、次のように定義されます:
たとえば、 のときは
となります。平方剰余の記号を具体的に計算すると
となります。だんだんとツイートの式に近づいてきました。
さてこのガウス和ですが、次の「とてもきれいな性質」が成り立ちます。
ガウス和の元々の定義は複雑そうなのに、その計算結果はとてもきれいなものになるのです!
tsujimotterはいつ見てもこの式は面白いなと思ってしまいます。
この定理1を証明したのはあのカール・フリードリヒ・ガウスです。だから「ガウス和」と呼ばれるんですね。
証明はやや込み入っているので、次回の記事で改めて紹介したいと思いますが、今回は定理1が成り立つことを受け入れて、計算してみましょう。
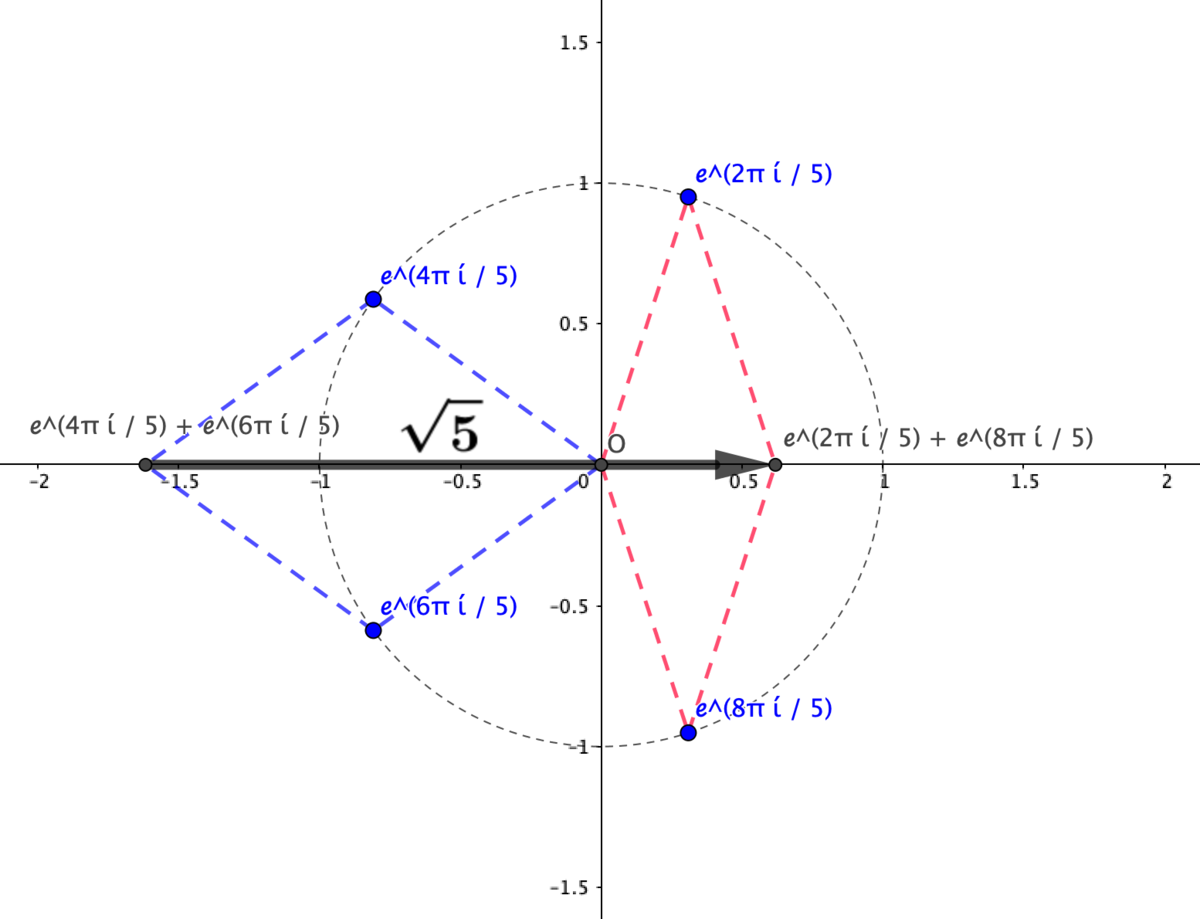
例1: の作り方
の作り方
やはり のときに考えると、
なので、定理1より
が成り立ちます。ガウス和の定義を展開した結果と比較すると
となります。目的の式まであと少しです。
ここで有名なオイラーの公式
を使うと
となります。
ところで、右辺を見ると実数ですので、左辺も実数でなければなりません。すなわち、虚部はすべて打ち消されるということです。
一方で、左辺の虚部は の項しかないので、
だけ考えればよいことになります。したがって
となります。
これが冒頭のツイートの式の一つだったというわけですね。
複素数平面で表すと、黒い太矢印の長さが になります。
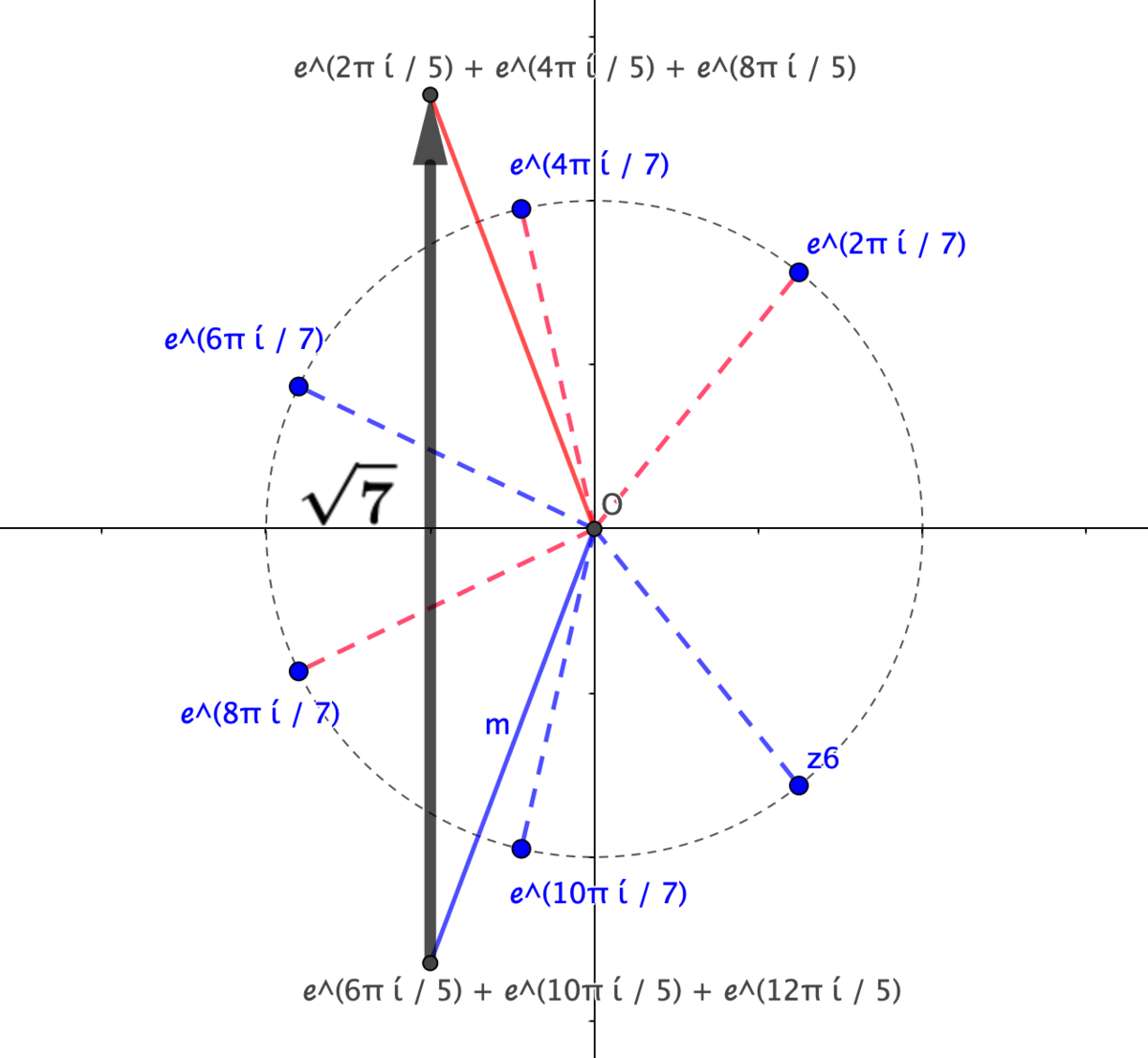
例2: の作り方
の作り方
のときも同様に計算できます。
が
の平方剰余であるような
は
の3つです。逆に、平方非剰余のリストは
となります。
(余談ですが、一般に平方剰余/平方非剰余の個数は一致します。)
また、 なので、定理1より
が得られるというわけです。
さて今度は で純虚数です。したがって、左辺は虚部、すなわち
の項だけ見ればよく
が得られることになります。
のときと同様に、複素数平面上で図形的に表現するとこんな感じになります。
ほかにも
以下同様に、任意の奇素数 に対して
を計算することで cos, sinを使って「
を作る式」をいくらでも作ることができます。
興味を持った方は、ぜひ自分でも計算してみてください!
それでは今日はこの辺で。
