(a○+b)×(a△+b)=(a□+b)になるa,bの条件と中国剰余定理

数学ファンの鯵坂もっちょさんがツイートしていた問題が面白かったので、今日はその問題について考えてみたいと思います。

あれ、もしかしてan+b(a,b,nは自然数、a,bは互いに素)型の数が積で閉じてるのってb=1のときだけか
— 鯵坂もっちょ🐟『つれづれなる数学日記』発売中 (@motcho_tw) 2021年5月31日

もっちょさんの問題は、任意の $a\text{○}+b, \; a\text{△}+b$ という形の数の積

$(a\text{○}+b) \times (a\text{△}+b)$

が再び

$a\text{□}+b$

と表せるような整数 $a, b$ の条件は？という問題ですね。

この問題、見た目以上に広がりがある問題だと思います。「中国剰余定理」や「天に向かって続く数」にもつながったりします。お楽しみに！

元の問題を解く

たとえば、 $7 = 3\cdot 2 + {\bf 1}$ 、 $13 = 3\cdot 4 + {\bf 1}$ とすると、どちらも $3n + {\bf 1}$ の形の数ですが、その積をとると

$7 \times 13 = 91$

となり、 $91 = 3 \cdot 10 + {\bf 1}$ なので $3n+{\bf 1}$ 型の数となっています。

一方で、 $3n+{\bf 2}$ 型の数では同じことにはなりません。

$11 \times 14 = (3\cdot 3 + {\bf 2}) \times (3\cdot 4 + {\bf 2}) = 154 = 3\cdot 50 + {\bf 4}$

どうも、 $an + b$ 型の数の $b$ の部分は $1$ でないとうまくいかないようです。

より正確に定式化すると、次の命題になるかと思います。

命題

$a, b \in \mathbb{Z}$ を整数とし、 $a, b$ を互いに素とする。このとき、次が成り立つ：

$\newcommand{\HLNO}{\unicode[\sans-serif,STIXGeneral]{x306E}}\begin{align*}&\text{任意}\HLNO{整数}\; n_1, n_2 \; \text{に対して整数} \; n_3 \; \text{が存在し}\; (an_1 + b)(an_2 + b)=an_3 + b \\ &\Longleftrightarrow \;\; b \equiv 1 \pmod{a} \end{align*}$

証明には初等整数論の基本的な事項を使います。

まず $an_1 + b$ と $an_2 + b$ の積は

$\begin{align*} (an_1 + b)(an_2 + b) &= a^2 n_1 n_2 + abn_1 + abn_2 + b^2 \\ &= a(a n_1 n_2 + bn_1 + bn_2) + b^2 \end{align*}$

と表せますので、 $a n_1 n_2 + bn_1 + bn_2 = n'$ とおくと

$(an_1 + b)(an_2 + b) = an' + b^2$

となります。

これがある整数 $n_3$ を用いて $an_3 + b$ と表せる必要十分条件は、 $\bmod{a}$ における合同式

$b^2 \equiv b \pmod{a} \tag{1}$

が成立することです。

あとは、 $(1)$ の必要十分条件が $b \equiv 1 \bmod{a}$ であることを示せばよいわけですね。

$b$ が $a$ と互いに素であるという条件を思い出すと、 $\bmod{a}$ における $b$ の逆元 $b^{-1}$ が存在します。したがって、 $b^{-1}$ を両辺にかけて

$b \equiv 1 \pmod{a} \tag{2}$

となり、目的の関係が得られます。逆に、式 $(2)$ の両辺に $b$ を掛ければ $(1)$ が得られるので、 $(1)$ と $(2)$ は同値です。

以上で命題の証明が完了したわけですが、面白いのは証明の途中に出てきた

$b^2 \equiv b \pmod{a} \tag{1再掲}$

という式です。

環 $\mathbb{Z}/a\mathbb{Z}$ で考えると、 $b$ は $b^2 = b$ を満たす元ということになりますね。このような元を冪等元といいます。つまり今回の問題は、 $\mathbb{Z}/a\mathbb{Z}$ の冪等元 $b$ の条件は？という問題だったわけですね。

今は、 $b$ は $a$ と互いに素、すなわち $b \in (\mathbb{Z}/a\mathbb{Z})^\times$ （ $\mathbb{Z}/a\mathbb{Z}$ の乗法群）の元に限定して考えています。そのような条件下では、 $\mathbb{Z}/a\mathbb{Z}$ の冪等元は $b = 1$ （乗法の単位元）しかないわけです。

せっかく $\mathbb{Z}/a\mathbb{Z}$ という環を考えたわけなので、今度は乗法群に限らない冪等元を探してみたいです。

$\mathbb{Z}/a\mathbb{Z}$ における冪等元、すなわち

$b^2 = b$

なる $b \in \mathbb{Z}/a\mathbb{Z}$ をすべて見つけられるでしょうか。

ここで使えるのが中国剰余定理です。

中国剰余定理（環論ver.）

中国剰余定理とは、互いに素な法 $m_1, m_2, \ldots, m_r$ における連立１次合同式に対し、その解を保証する定理です。

任意の $r$ 個の整数 $a_1, a_2, \ldots, a_r$ に対して、　

$\begin{cases} x \equiv a_1 \pmod{m_1} \\ x \equiv a_2 \pmod{m_2} \\ \vdots \\ x \equiv a_r \pmod{m_r} \end{cases} \tag{3}$

を満たす整数 $x$ の存在が保証されるわけですね。さらにその解は $\bmod{m_1 m_2 \cdots m_r}$ で一意的です。

具体的には、たとえば $3$ で割ってあまり $2$ で、 $5$ で割ってあまり $4$ 、 $7$ で割ってあまり $2$ であるような数はあるか、という問題を考えてみましょう。つまり、連立合同式

$\begin{cases} x \equiv 2 \pmod{3} \\ x \equiv 4 \pmod{5} \\ x \equiv 2 \pmod{7} \end{cases} \tag{4}$

の解 $x$ は存在するか、という問題ですね。

実際、 $x = 44$ とすると上記の合同式をすべて満たすことがわかります。このような解があることを保証するのが中国剰余定理というわけですね。

さらにいえば、 $x = 44 + 105n$ （ $n$ は整数）という形の一般解があるわけですが、 $\bmod{105}$ で考えれば $x \equiv 44 \pmod{105}$ となり、一意的に解が定まるというわけです。

中国剰余定理については、もっちょさんによる大変分かりやすい解説がありますので、参考に置いておきます。
www.ajimatics.com

さて、今日考えたいのは、もう少し洗練されたバージョンの中国剰余定理です。

連立合同式 $(4)$ の条件は、 $\mathbb{Z}/3\mathbb{Z}$ 、 $\mathbb{Z}/5\mathbb{Z}$ 、 $\mathbb{Z}/7\mathbb{Z}$ という３つの集合の直積の元

$(2, 4, 2) \in \mathbb{Z}/3\mathbb{Z} \times \mathbb{Z}/5\mathbb{Z} \times \mathbb{Z}/7\mathbb{Z}$

だと思うことができます。これに対して $\mathbb{Z}/105\mathbb{Z}$ の元 $x$ が定まるというのが中国剰余定理の主張でした。

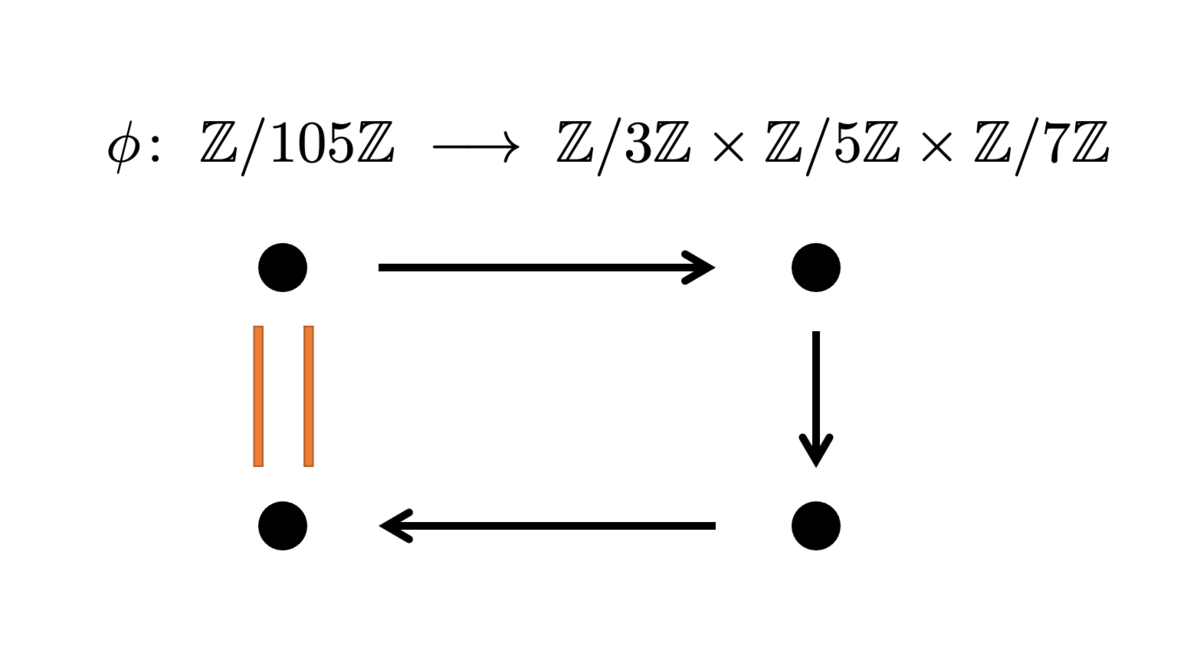
これはすなわちこういうことです。写像

$\phi\colon \; \mathbb{Z}/105\mathbb{Z} \; \longrightarrow \; \mathbb{Z}/3\mathbb{Z} \times \mathbb{Z}/5\mathbb{Z} \times \mathbb{Z}/7\mathbb{Z}$

を考えます。ただし、これは $x \in \mathbb{Z}/105\mathbb{Z}$ に対して

$\phi(x) = ( x\bmod{3}, \; x\bmod{5}, \; x\bmod{7} )$

を対応させる写像です。

中国剰余定理が主張するのは、行き先の任意の組み合わせに対して、そこに向かう $x$ が存在すると言っているわけですから、つまり $\phi$ が全射だといっているわけです。このように言い換えられるのは面白いですね。

また、 $\bmod{105}$ で一意的ということは、これは単射でもあるということを言っています。つまり、 $\phi$ は全単射というわけですね。

ここまでは古典的な中国剰余定理と何も変わらない（単に言い換えただけ）ですが、ここからさらに話を進めましょう。

$\phi$ という写像は、 $\mathbb{Z}/105\mathbb{Z}$ という集合から、 $\mathbb{Z}/3\mathbb{Z} \times \mathbb{Z}/5\mathbb{Z} \times \mathbb{Z}/7\mathbb{Z}$ という集合への写像として定義されたのですが、これを環から環への写像であると考えましょう。

さらに、この $\phi$ という写像は環準同型写像になっているのです。環準同型とは、環の演算をそのまま保つような写像というわけです。特に、環準同型かつ全単射なので、環同型写像にもなっています。

環準同型写像とは、具体的には定義域の元 $x, y \in \mathbb{Z}/105\mathbb{Z}$ に対して、次のようなことが成り立つものを指します：

$\begin{align*} \phi(x + y) &= ( x + y\bmod{3}, \; x + y\bmod{5}, \; x + y\bmod{7} ) \\ &= ( x\bmod{3}, \; x\bmod{5}, \; x\bmod{7} ) + ( y\bmod{3}, \; y\bmod{5}, \; y\bmod{7} ) \\ &= \phi(x) + \phi(y) \end{align*}$

$\begin{align*} \phi(xy) &= ( xy\bmod{3}, \; xy\bmod{5}, \; xy\bmod{7} ) \\ &= ( x\bmod{3}, \; x\bmod{5}, \; x\bmod{7} ) \cdot ( y\bmod{3}, \; y\bmod{5}, \; y\bmod{7} ) \\ &= \phi(x) \phi(y) \end{align*}$

これは一見すると「当たり前じゃん」と思われてしまいそうな性質ですが、これがとても大事です。

というのも、この性質によって、 $\mathbb{Z}/105\mathbb{Z}$ と $\mathbb{Z}/3\mathbb{Z} \times \mathbb{Z}/5\mathbb{Z} \times \mathbb{Z}/7\mathbb{Z}$ が自在に行き来できるからです。

① $\mathbb{Z}/105\mathbb{Z}$ で計算した結果と、②一旦 $\phi$ で $\mathbb{Z}/3\mathbb{Z} \times \mathbb{Z}/5\mathbb{Z} \times \mathbb{Z}/7\mathbb{Z}$ に移して計算した結果を $\phi^{-1}$ で戻してきたものは、一般に等しくなります。

たとえば、① $\mathbb{Z}/105\mathbb{Z}$ で計算した $b^2 = b$ の解 $b$ と、② $\bmod{3}, \bmod{5}, \bmod{7}$ でそれぞれ求めた $b^2 = b$ の解 $(b_1, b_2, b_3)$ を $\mathbb{Z}/105\mathbb{Z}$ に戻してきて得られた $b$ が一致するわけです。

実際、 $\mathbb{Z}/105\mathbb{Z}$ において $b$ が

$b^2 = b$

を満たすとします。ここで、両辺を $\phi$ を使って写すと、等号

$\phi(b^2) = \phi(b)$

が成り立ちます。（同じ元からの写像の行き先は等しい $x = y \; \Longrightarrow \; \phi(x) = \phi(y)$ を使った。）

$\phi$ は環準同型なので、左辺は $\phi(b^2) = \phi(b)^2$ より

$\phi(b)^2 = \phi(b)$

と表せます。この式は環 $\mathbb{Z}/3\mathbb{Z} \times \mathbb{Z}/5\mathbb{Z} \times \mathbb{Z}/7\mathbb{Z}$ における $x^2 = x$ の解が $\phi(b)$ であることを表していますね。

このようにして得られた解 $\phi(b)$ を $\phi^{-1}$ によって戻してくれば $\phi^{-1}( \phi(b) ) = b$ となり、元々の $b^2 = b$ を満たす $b \in \mathbb{Z}/105\mathbb{Z}$ が得られると言うわけです。（ $\phi$ は全単射なので $\phi^{-1}$ が存在することを使った。）

この議論のイメージは以下の通りです：

だんだんやりたいことがわかってきましたか？

中国剰余定理を使って冪等元を求める

元々、求めたかったのは

$b^2 \equiv b \pmod{a}$

の整数解 $b$ でした。

つまり環 $\mathbb{Z}/a\mathbb{Z}$ の言葉で言うと

$b^2 = b \tag{5}$

を満たす $b \in \mathbb{Z}/a\mathbb{Z}$ を求めよという問題ですね。これを中国剰余定理を使って考えてみましょう。

まず、 $a$ を素因数分解します。

$a = p_1^{e_1} p_2^{e^2} \cdots p_r^{e_r} \tag{6}$

$p_1, p_2, \ldots, p_r$ は相異なる $a$ の素因数として、その個数を $r$ としています。

さて、ここで $p_1^{e_1}, \; p_2^{e^2}, \; \ldots , \; p_r^{e_r}$ はそれぞれ互いに素であることに注意しましょう。中国剰余定理が適用できて、環同型

$\mathbb{Z}/a\mathbb{Z} \simeq \mathbb{Z}/p_1^{e_1}\mathbb{Z} \times \mathbb{Z}/p_2^{e^2}\mathbb{Z} \times \cdots \times \mathbb{Z}/ p_r^{e_r}\mathbb{Z} \tag{7}$

が得られます。

これによって、 $\bmod{a}$ の問題を $\bmod{p_1^{e_1}}, \; \bmod{p_2^{e_2}}, \; \ldots, \; \bmod{p_r^{e_r}}$ に帰着できるわけです。

あとは、 $\mathbb{Z}/p^e \mathbb{Z}$ （素数冪）において

$b^2 = b$

の解を求めればよいことになります。

実は、法が素数冪のときにおいては、次が成り立ちます：

素数 $p$ と正の整数 $e$ に対して、整数 $b$ が

$b^2 \equiv b \pmod{p^e}$

を満たすならば、 $b \equiv 0\pmod{p^e}$ または $b \equiv 1\pmod{p^e}$ である。

これは証明すべきことなので、証明しましょう。

（証明）
整数 $b$ が $b^2 \equiv b \pmod{p^e}$ を満たすとします。

すると

$b(b-1) \equiv 0\pmod{p^e}$

より、 $b$ または $b-1$ が $p$ で割り切れることになります。

(i) $b$ が $p$ で割り切れるとき：
$b-1$ も $p$ で割り切れるとすると、 $b - (b-1) = 1$ も $p$ で割り切れることになるため、 $b-1$ は $p$ で割り切れません。

したがって、 $b$ が $p^e$ で割り切れることになり、 $b \equiv 0 \pmod{p^e}$ が成り立ちます。

(ii) $b-1$ が $p$ で割り切れるとき：
$b$ も $p$ で割り切れるとすると、 $b - (b-1) = 1$ も $p$ で割り切れることになるため、 $b$ は $p$ で割り切れません。

したがって、 $b-1$ が $p^e$ で割り切れることになり、 $b \equiv 1 \pmod{p^e}$ が成り立ちます。

（証明おわり）

以上により、 $\bmod{p^e}$ における $b^2 \equiv b$ の解は $0, 1$ のいずれかであることが分かりました。

したがって、環の直積

$\mathbb{Z}/p_1^{e_1}\mathbb{Z} \times \mathbb{Z}/p_2^{e^2}\mathbb{Z} \times \cdots \times \mathbb{Z}/ p_r^{e_r}\mathbb{Z}$

における $b^2 = b$ の解は、それぞれの因子における $0, 1$ のすべての組み合わせとなります。

すなわち

$(b_1, b_2, \ldots, b_r) = (0, 0, \ldots, 0), \; (0, 0, \ldots, 1), \; \ldots, \; (1, 1, \ldots, 0), \; (1, 1, \ldots, 1)$

の $2^r$ 個が解となります。

ここまでが環の直積の方の解となるわけですが、これを $\mathbb{Z}/a\mathbb{Z}$ に戻してくれば問題解決です。

環同型は特に全単射なので、全射性より $(b_1, b_2, \ldots, b_r)$ に対応する $\mathbb{Z}/a\mathbb{Z}$ の元が存在します。さらに単射性より、その関係は１対１なので、先ほどの $2^r$ 個の解に対応する解が $\mathbb{Z}/a\mathbb{Z}$ にそれぞれ存在します。

したがって $\mathbb{Z}/a\mathbb{Z}$ における

$b^2 = b$

の解（すなわち、冪等元）の個数は $2^r$ 個というわけですね。

具体例１

一般論としてはここまでですが、 $a$ に適当な整数を入れると、具体的な冪等元が計算できます。やってみましょう。

$a = 105 = 3\times 5 \times 7$ とし、 $\mathbb{Z}/105\mathbb{Z}$ における

$b^2 = b$

の解を求めましょう。

中国剰余定理によって、環の同型

$\phi\colon \; \mathbb{Z}/105\mathbb{Z} \; \simeq \; \mathbb{Z}/3\mathbb{Z} \times \mathbb{Z}/5\mathbb{Z} \times \mathbb{Z}/7\mathbb{Z}$

がありますので、右辺で考えます。

実際

$b_1^2 \equiv b_1 \pmod{3}$

$b_2^2 \equiv b_2 \pmod{5}$

$b_3^2 \equiv b_3 \pmod{7}$

の解の組み合わせとしては

$\begin{align*} (b_1, b_2, b_3) \equiv \; &(0, 0, 0), \; (0, 0, 1), \; (0, 1, 0), \; (0, 1, 1), \\ &(1, 0, 0), \; (1, 0, 1), \; (1, 1, 0), \; (1, 1, 1) \end{align*}$

の $2^3$ 通りです。

上の環同型によって、これらに対応する元がそれぞれ一つずつ存在します。実際

$\phi(0) = (0, 0, 0)$

$\phi(1) = (1, 1, 1)$

$\phi(15) = (0, 0, 1)$

$\phi(21) = (0, 1, 0)$

$\phi(36) = (0, 1, 1)$

$\phi(70) = (1, 0, 0)$

$\phi(85) = (1, 0, 1)$

$\phi(91) = (1, 1, 0)$

となります。（これは素朴に計算するほかありません。）

よって

$b = 0, 1, 15, 21, 36, 70, 85, 91$

の $8$ 個が $\mathbb{Z}/105\mathbb{Z}$ において $b^2 = b$ を満たす元、すなわち冪等元ということになるわけですね。
（確認してみると、確かにそうなっています。）

$a = 105$ に対して、 $b = 21$ を選び、元々の問題

$(105n_1 + 21)\times (105n_2 + 21)$

を計算してみましょう。

式変形すると

$\begin{align*} (105n_1 + 21)\times (105n_2 + 21) = 105(105n_1n_2 + 21n_1 + 21n_2) + 21^2 \end{align*}$

となります。ここで、先ほどの議論により

$21^2 \equiv 21 \pmod{105}$

となっているはずですが、実際

$21^2 = 441 = 21 + 105\cdot 4$

となります。したがって

$\begin{align*} (105n_1 + 21)\times (105n_2 + 21) = 105\;\underline{(105n_1n_2 + 21n_1 + 21n_2 + 4)} + 21 \end{align*}$

が成り立つというわけですね。よって、下線部を $n_3$ とすれば

$\begin{align*} (105n_1 + 21)\times (105n_2 + 21) = 105n_3 + 21 \end{align*}$

が成り立つというわけです。

具体例２

他にも $a = 36 = 2^2 \times 3^2$ を考えてみましょう。

中国剰余定理によって、環の同型

$\phi\colon \; \mathbb{Z}/36\mathbb{Z} \; \simeq \; \mathbb{Z}/2^2\mathbb{Z} \times \mathbb{Z}/3^2\mathbb{Z}$

がありますので、右辺で考えます。

中国剰余定理による各因子は互いに素でなければいけませんので

$\mathbb{Z}/2\mathbb{Z} \times \mathbb{Z}/2\mathbb{Z} \times \mathbb{Z}/3\mathbb{Z} \times \mathbb{Z}/3\mathbb{Z}$

のようにはできないことに注意。

実際

$b_1^2 \equiv b_1 \pmod{2^2}$

$b_2^2 \equiv b_2 \pmod{3^2}$

の解の組み合わせとしては

$\begin{align*} (b_1, b_2) \equiv (0, 0), \; (0, 1), \; (1, 0), \; (1, 1) \end{align*}$

の $2^2$ 通りです。

上の環同型によって、これらに対応する元がそれぞれ一つずつ存在します。実際

$\phi(0) = (0, 0)$

$\phi(1) = (1, 1)$

$\phi(9) = (1, 0)$

$\phi(28) = (0, 1)$

となります。（これも素朴に計算するほかありません。）

よって

$b = 0, 1, 9, 28$

の $4$ 個が $\mathbb{Z}/36\mathbb{Z}$ において $b^2 = b$ を満たす元、すなわち冪等元ということになるわけですね。
（確認してみると、確かにそうなっています。）

「天に向かって続く数」との関係

今回の話を見て、加藤文元先生・中井保行先生の「天に向かって続く数」の話を思い出した方もいるかもしれません。

天に向かって続く数

作者:加藤文元,中井保行
日本評論社

Amazon

ペレルマン数という数がありまして

$\begin{align*} 5^2 &\equiv 5 \pmod{10} \\ 25^2 &\equiv 25 \pmod{100} \\ 625^2 &\equiv 625 \pmod{1000} \\ 625^2 &\equiv 625 \pmod{10000} \\ 90625^2 &\equiv 90625 \pmod{100000} \\ 890625^2 &\equiv 890625 \pmod{1000000} \\ &\vdots \end{align*}$

という無限に続く合同式が得られるというものです。これを単に

$b_1 = \ldots 890625$

と表しましょう。

他の系列としては

$\begin{align*} 6^2 &\equiv 6 \pmod{10} \\ 76^2 &\equiv 76 \pmod{100} \\ 376^2 &\equiv 376 \pmod{1000} \\ 9376^2 &\equiv 9376 \pmod{10000} \\ 9376^2 &\equiv 9376 \pmod{100000} \\ 109376^2 &\equiv 109376 \pmod{1000000} \\ &\vdots \end{align*}$

というものもあります。

これも

$b_2 = \ldots 109376$

のように表記しましょう。

もう少し自明なものだと

$\begin{align*} 0^2 &\equiv 0 \pmod{10} \\ 0^2 &\equiv 0 \pmod{100} \\ 0^2 &\equiv 0 \pmod{1000} \\ 0^2 &\equiv 0 \pmod{10000} \\ 0^2 &\equiv 0 \pmod{100000} \\ 0^2 &\equiv 0 \pmod{1000000} \\ &\vdots \end{align*}$

というものや

$\begin{align*} 1^2 &\equiv 1 \pmod{10} \\ 1^2 &\equiv 1 \pmod{100} \\ 1^2 &\equiv 1 \pmod{1000} \\ 1^2 &\equiv 1 \pmod{10000} \\ 1^2 &\equiv 1 \pmod{100000} \\ 1^2 &\equiv 1 \pmod{1000000} \\ &\vdots \end{align*}$