小数展開にフィボナッチ数列 etc. が出てくる分数（前編）

日曜数学 Advent Calendar 2021 の1日目の記事です。

アドベントカレンダーの季節がやってまいりました。今年も日曜数学アドベントカレンダーを立てまして、この記事はその1日目の記事となっています。
adventar.org

日曜数学アドベントカレンダーは、今年で 7年目になります。なかなか続いていますね。

まだまだ空きはありますので、よろしければご参加お待ちしています。みなさまの記事を楽しみにしています！

トップバッターのこの記事では

$\displaystyle \frac{100}{9899} \tag{1}$

という分数について考えてみましょう。

実際に計算して、小数展開を求めてみるとこうなります：

$\displaystyle \require{color} \frac{100}{9899} = {\color[rgb]{1.000000,0.000000,0.200000}0.01010203050813213455}90463\ldots \tag{2}$

小数部分を2桁ずつ区切ってみると

$\displaystyle {\color[rgb]{1.000000,0.000000,0.200000}0.\;01\;01\;02\;03\;05\;08\;13\;21\;34\;55}\;90\;46\;3\ldots$

となりますが、ここから

$\displaystyle {\color[rgb]{1.000000,0.000000,0.200000}0, \; 1, \;1, \;2, \;3, \;5, \;8, \;13, \;21, \;34, \;55}$

という数列が得られますね。

この数列、なんとフィボナッチ数列になっているのです！　面白いですよね！

f:id:tsujimotter:20211130174416p:plain:w480

いったいどういう仕組みでフィボナッチ数列が出てくるのでしょうか。今日はその理屈を解説したいと思います。

フィボナッチ数列以外にも、同様の仕組みで数列の値が小数展開に出てくる分数を作ることができます。これについても紹介したいと思います。（後編の記事で紹介します。）

それでは、最後までぜひご覧ください！

なお、今回の記事では、分数の小数展開を計算することが必要になります。電卓で計算する際は、桁数に限界があり不便です。

そこで以下のページで、小数展開を任意の計算精度で出せるようにしてみました！　自分で計算してみると楽しいので、よろしければご活用ください。
tsujimotter.info

母関数

今回のキーワードは数列の母関数です。

数列 $a_n$ が何か一つ与えられたとしましょう。このとき

$\displaystyle \sum_{n=0}^{\infty} a_n X^n = a_0 + a_1 X + a_2 X^2 + a_3 X^3 + \cdots \tag{3}$

を $a_n$ の母関数といいます。

要するに、 $X^n$ の係数に $a_n$ が出てくるような関数を考えるというわけですね。定数項の部分には、 $X^0$ の係数だと思って $a_0$ を置くことにします。

上の母関数は、無限級数の形で表されていますが、もしこの関数を閉じた式で表すことができたとしましょう。それを $f(X)$ とおきます。

ここで、 $X = 1/10$ を代入すると

$\displaystyle f(1/10) = a_0 + a_1 10^{-1} + a_2 10^{-2} + a_3 10^{-3} + \cdots \tag{4}$

と表すことができます。もし、 $a_1, a_2, a_3, a_4$ が1桁の数列であれば、 $f(1/10)$ の小数点以下3桁までに $a_0.a_1a_2a_3\ldots$ のように数列の値が出てくるという寸法です。これが今回の話のトリックです。

同じように、 $X = 1/100$ を代入すると小数展開に2桁ずつ、 $X = 1/1000$ を代入すると小数展開に3桁ずつ数列が出てくることになります。

実際に、わかりやすい例として、初項 $a_0 = 1$ で、公比が $r$ であるような等比数列を考えることにしましょう。

$\begin{align} a_0 &= 1, \\ a_1 &= r, \\ a_2 &= r^2 \\ a_3 &= r^3 \\ a_4 &= r^4 \\ &\vdots \end{align}$

を考えます。この数列の母関数を考えると

$\displaystyle \sum_{n=0}^{\infty} a_n X^n = 1 + rX + r^2 X^2 + r^3 X^3 + \cdots \tag{5}$

となります。これは、公比が $rX$ の等比数列だと思うことができます。

したがって、無限等比数列の和公式を用いて

$\displaystyle 1 + rX + r^2 X^2 + r^3 X^3 + \cdots = \frac{1}{1-rX} \tag{6}$

と表すことができますね。

ここで、 $f(X) = \frac{1}{1-rX}$ とおけば、母関数の閉じた形が得られたことになります。

たとえば公比を $r = 2$ とすると、

$\displaystyle f(X) = \frac{1}{1-2X} \tag{7}$

と置けるわけですが、 $X = 1/100$ を代入すると

$\displaystyle f(1/100) = \frac{1}{1-\frac{2}{100}} = \frac{50}{49} \tag{8}$

したがって、 $50/49$ の小数展開を計算して2桁ずつに区切ると、 $a_n = 2^n$ が出てくるというわけです。

実際

$\displaystyle \frac{50}{49} = 1.02040816326530 \tag{9}$

となり、ちゃんと $1, 2, 4, 8, 16, 32$ が出ていることがわかりますね。

その後の $65, 30$ が例外っぽく見えていますが、これは繰り上がりのせいです。実際、本来続く数列は $64, 128$ のはずなのですが、 $128$ に3桁目があるせいで、 $64$ の1桁目にこれが足されてしまって $65$ になっているわけです。 $30$ の方も同様で、続く $256$ の3桁目が $28$ の1桁目に加算されてしまっています。

というわけで、完全にすべての数列を出し続けるのは不可能なのですが、途中までは数列をきれいに出力することができます。

また、正確に出力できる桁数をコントロールするためには、 $X = 1/100$ のところを $X = 1/1000$ にしたり、 $X = 1/10000$ にしたり、 $X$ の桁数を調整すればよいことになります。

逆に、 $X = 1/10$ とするとどうなるでしょうか。

計算すると

$\displaystyle f(1/10) = \frac{1}{1-\frac{2}{10}} = \frac{5}{4}$

となり、かなり綺麗な分数になってしまいました。

これを小数展開すると

$\displaystyle \frac{5}{4} = 1.25$

となるわけですが、いったいどこに等比数列 $2^n$ があるというのでしょうか。

これについては

$\displaystyle \frac{5}{4} = 1.249999\ldots$

と考えるといいかもしれません。

つまり、繰り上がりも含めて考えればよくて、等比数列 $2^n$ を1桁ずつずらしながら足していくと

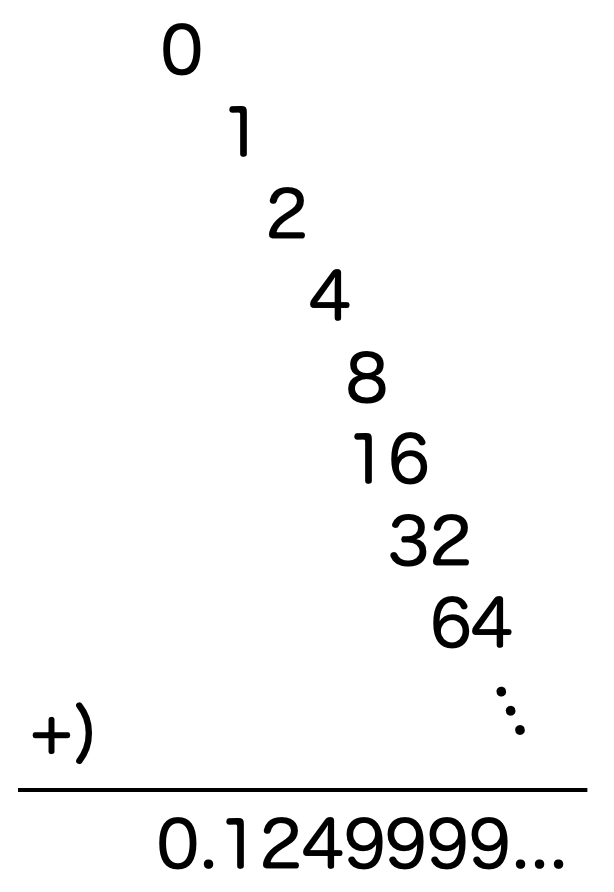
f:id:tsujimotter:20211130193622p:plain:w180

のように、和がちょうど 9999... になるというわけなんですね。等比数列が互いに協力して 9999... を作っているような・・・！

なんというか、数学ってうまいことできていますね！

フィボナッチ数列が出てくる仕組み

ここまで考えると、冒頭に出てくる式も、フィボナッチ数列 $F_n$ の母関数を考えれば良いと気づくでしょう。

$\displaystyle \sum_{n=0}^\infty F_n X^n = F_0 + F_1 X + F_2 X^2 + F_3 X^3 + \cdots \tag{10}$

念のため書いておくと、ここでのフィボナッチ数列は

$F_0 = 0, \; F_1 = 1, \; F_2 = 1, \; F_3 = 2, \; F_4 = 3, \; F_5 = 5, \; \ldots \tag{11}$

のように続く数列のことで、 $n \geq 2$ について

$F_n = F_{n-1} + F_{n-2} \tag{12}$

なる漸化式によって帰納的に定義されます。

このとき、フィボナッチ数列の母関数は、次のような閉じた式で表すことができます：

$\displaystyle \sum_{n=0}^\infty F_n X^n = \frac{X}{1-X-X^2} \tag{13}$

これを証明したいと思います。

ちなみに文献によっては、フィボナッチ数列の母関数を

$\displaystyle \sum_{n=0}^\infty F_n X^n = \frac{1}{1-X-X^2} \tag{14}$

のように書いているものもあります。ここで混乱した人もいるかもしれません。

式 $(14)$ の場合は、フィボナッチ数の定義が異なっていて、

$F_0 = 1, \; F_1 = 1, \; F_2 = 2, \; F_3 = 3, \; \ldots$

のようになっているかと思います。つまり、フィボナッチ数列のインデックスが１個ずれているわけですね。

あるいは、母関数の和のインデックスが $n = 0$ からではなく $n = 1$ からになっているかもしれません。この辺に注意をすると良いかと思います。

さて、式 $(13)$ を証明するにあたっては、両辺に $1-X-X^2$ をかけた

$\displaystyle (1-X-X^2) \sum_{n=0}^\infty F_n X^n = X \tag{15}$

を示せば良いことになります。

左辺を変形すると、次のように右辺の式が得られることになります。

$\displaystyle \begin{align} (\text{左辺}) &= (1-X-X^2) \sum_{n=0}^\infty F_n X^n \\ &= \sum_{n=0}^\infty F_n X^n - X\sum_{n=0}^\infty F_n X^n - X^2\sum_{n=0}^\infty F_n X^n \\ &= \sum_{n=0}^\infty F_n X^n - \sum_{n=0}^\infty F_n X^{n+1} - \sum_{n=0}^\infty F_n X^{n+2} \\ &= \sum_{n=0}^\infty F_n X^n - \sum_{n=1}^\infty F_{n-1} X^{n} - \sum_{n=2}^\infty F_{n-2} X^{n} \\ &= F_0 + F_1 X - F_0X + \sum_{n=2}^\infty F_n X^n - \sum_{n=2}^\infty F_{n-1} X^{n} - \sum_{n=2}^\infty F_{n-2} X^{n} \\ &= F_0 + F_1 X - F_0X + \sum_{n=2}^\infty (F_n - F_{n-1} - F_{n-2}) X^n \\ &= 0 + 1\cdot X - 0\cdot X + \sum_{n=2}^\infty 0\cdot X^n \\ &= X \\ &= (\text{右辺}) \end{align}$

これにて証明完了です。

そんなわけで、フィボナッチ数列の母関数の閉じた式

$\displaystyle f(X) = \frac{X}{1-X-X^2} \tag{16}$

が得られました。

あとは、これに $X = 1/100$ を代入すると

$\displaystyle f(1/100) = \frac{\frac{1}{100}}{1-\frac{1}{100}-\left(\frac{1}{100}\right)^2} = \frac{100}{10000 - 100 - 1} = \frac{100}{9899} \tag{17}$