日曜化学(2)：3次元空間における電子雲の計算（Python/matplotlib）

２日前に公開した量子力学に関する記事なのですが、たくさんの方に見ていただいて嬉しいです。Twitter上でもたくさんの嬉しいコメントをいただきました。
tsujimotter.hatenablog.com

今日は続きとして、電子雲の可視化をしたいと思います。

前回の記事では、水素原子におけるシュレディンガー方程式

$\displaystyle \hat{H}\Psi = E \Psi \tag{1}$

を考えました。 $\Psi$ は波動関数で $E$ はエネルギー。 $\hat{H}$ はハミルトニアンという演算子で、定義は次の通りです：

$\displaystyle \newcommand{\d}{\partial}\displaystyle \hat{H} = -\frac{\hbar}{2m_e}\left(\frac{\d^2}{\d x^2} + \frac{\d^2}{\d y^2} + \frac{\d^2}{\d z^2} \right) + V({\bf r}) \tag{2}$

この方程式をデカルト座標 $(x, y, z)$ から球面座標系 $(r, \theta, \phi)$ に直して、変数分離によって解を求めるという方法を紹介しました。

変数分離

$\Psi(r, \theta, \phi) = R(r) \, Y(\theta, \phi) \tag{3}$

によって、動径波動関数 $R(r)$ と球面調和関数 $Y(\theta, \phi)$ に分けられるわけですが、前回の記事では特に球面調和関数 $Y(\theta, \phi)$ について可視化を行いました。

しかしながら、球面調和関数が教えてくれるのは「どの方向に電子が多く分布しているか」という情報です。これだけだと「３次元の中でどの辺に電子が分布しているのか」という情報はわかりません。この情報を知るためには「動径方向」の分布を調べる必要があり、したがって $R(r)$ を計算する必要があります。

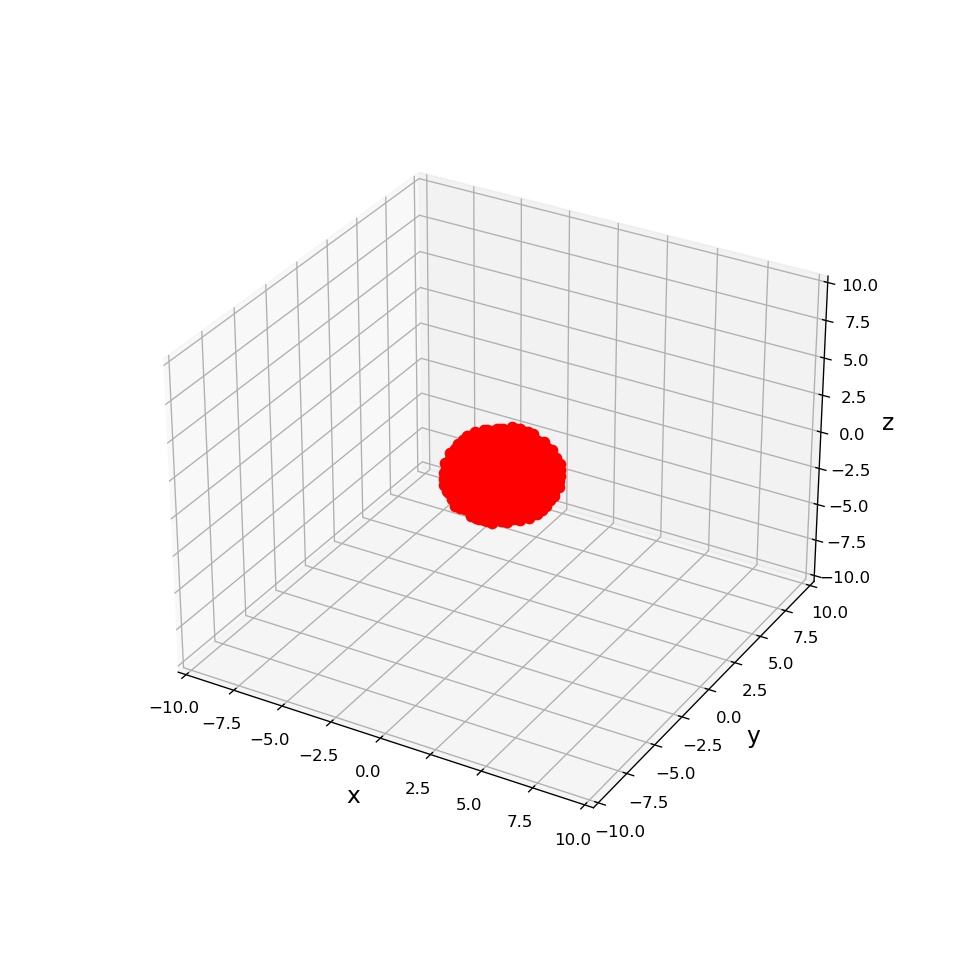
そこで、今日は動径方向の分布を考慮に入れて、実際に電子雲の計算をしてみようと思います。最終的には、Pythonのmatplotlibを用いて次のような図を描くのを目標としたいと思います。

f:id:tsujimotter:20210704033300j:plain:w300

実際、3次元での電子分布を考えるにあたっては、それなりに工夫が必要です。上記の図では「確率密度関数の積分値が90%になる領域をプロットするテクニック」を使っているのですが、なかなか実装するのが難しいのでそれについても解説したいと思います。

前回同様、Pythonのmatplotlibを使ったプログラムも掲載しますので、よかったら遊んでみてください。

GIF画像も作ってみました！　楽しいですね！

f:id:tsujimotter:20210704131328g:plain:w400

目次：

1. 動径波動関数の計算

2. 三次元空間における電子雲をいかに計算するか？

方法１：次元を落とす

方法２：散布図としてプロット

方法３：確率90%となるような領域を可視化

3. 補足：有効核電荷とスレーター則

次回予告

参考文献

追記（Plotlyを使用した可視化）：

1. 動径波動関数の計算

まずは、動径波動関数 $R(r)$ を計算したいと思います。

前回の記事を思い出すと、 $R(r)$ が満たす微分方程式は次のものでした：

$\displaystyle \frac{\d}{\d r}\left( r^2 \frac{\d}{\d r} \right) R(r) + \frac{2m_e r^2}{\hbar}(E - V(r) ) R(r) = l(l+1) R(r) \tag{4}$

また、水素原子のポテンシャルは

$\displaystyle V(r) = -\frac{a}{r}$

と表されるのでした。今回は定数 $a$ の部分も具体的に必要になりますので

$\displaystyle V(r) = -\frac{Ze^2}{4\pi \varepsilon_0 r}$

としておきましょう。ここで、 $Z$ は原子核の電荷です。水素原子を考える場合は $Z = 1$ でいいわけですが、一般化しやすいように最初から電荷は $Z$ としておきます。

残りの定数の定義は次の通り：

$e$ 素電荷量（電子の電荷量）
$\varepsilon_0$ 真空の誘電率
$\pi$ 円周率

あとは、これは解けば良い・・・のですが、やはり簡単では無いようです。今回はおとなしく解を持ってきたいと思います。

動径波動関数 $R(r)$ は、主量子数 $n$ と方位量子数 $l$ を用いて $R_{n,l}(r)$ と表されるものだけが解となります。具体的には次のようになります：

動径波動関数 $R(r)$

$\displaystyle R_{n,l} = N_{n,l} \, e^{-\rho_n(r) / 2} \, ( \rho_n(r) )^l \, L_{n+l}^{2l+1}( \rho_n(r) ) \tag{6}$

注意2022.02.07：式 $(6)$ のラゲール陪多項式 $L_{n+l}^{2l+1}( \rho_n(r) )$ の添字は正しくは $L_{n-l-1}^{2l+1}( \rho_n(r) )$ なのでは、というご指摘を受けています。私自身、まだ真偽を確かめてられておりません。
確認にしばらく時間がかかりそうなので、一旦注意喚起としてこちらに記載させていただきます。

注意2022.02.16：上記の注意ですが、元のままでも問題ないことが分かりました。問題はラゲール陪多項式の種類が2種類あることで、その違いに起因するものでした。余裕があるときに、これについて補足したいと思います。

かなり複雑な式となっていますが、１つ１つ見ていきましょう。

$N_{n, l}$ ：

規格化定数。これについては後で考えますが、積分値が $1$ になるように辻褄を合わせるための、単なる定数なのであまり気にしなくてよいです。

$\rho_n(r)$ ：

半径 $r$ に対して定まる関数であり、定義は次の通り。

$\displaystyle \rho_n(r) = \frac{2Z}{na_0} r$

要するに、 $r$ に比例定数をつけただけのものです。 $a_0$ はボーア半径と呼ばれるもので、その意味はだいたい水素原子の原子核のサイズを表す定数です。（物理的な意味はあとで説明します。）
ボーア定数の定義は

$\displaystyle a_0 = \frac{4\pi \varepsilon_0 \hbar^2}{m_e e^2}$

です。計算すると、だいたい 52.9 [pm] となります。

$L_{n+l}^{2l+1}(x)$ ：

ラゲールの倍多項式と呼ばれる関数です。前回のルジャンドルの倍多項式と同じように、微分方程式を解くために出てくる多項式です。この多項式に $x = \rho_n(r)$ を代入するわけですね。

定義はやはり複雑なので、具体的な式を知りたい方はEmanさんのページをご覧になってください：
eman-physics.net
（すぐあとで具体的な計算結果だけは出しますので、今回の記事の中ではとりあえずは中身を知らなくても大丈夫です。）

そんなわけで、ラゲールの倍多項式に指数関数がかかったような形をしているわけですね。

とはいえ、このままでは掴み所がないので、具体的な計算結果を見た方がいいかもしれません。以下では、 $n = 1, 2, 3$ のときの結果を紹介します。

$n = 1$ のとき	$\displaystyle R_{1,0}(r) = \left(\frac{Z}{a_0}\right)^{\frac{3}{2}} e^{-\rho_1(r) / 2} \cdot 2$ 　（1s軌道）
$n = 2$ のとき	$\displaystyle R_{2,0}(r) = \left(\frac{Z}{a_0}\right)^{\frac{3}{2}} e^{-\rho_2(r) / 2} \cdot \frac{1}{2\sqrt{2}} (2 - \rho_2(r) )$ 　（2s軌道） $\displaystyle R_{2,1}(r) = \left(\frac{Z}{a_0}\right)^{\frac{3}{2}} e^{-\rho_2(r) / 2} \cdot \frac{1}{2\sqrt{6}} \rho_2(r)$ 　（2p軌道）
$n = 3$ のとき	$\displaystyle R_{3,0}(r) = \left(\frac{Z}{a_0}\right)^{\frac{3}{2}} e^{-\rho_3(r) / 2} \cdot \frac{1}{9\sqrt{3}} (6 - 6\rho_3(r) + (\rho_3(r) )^2 )$ 　（3s軌道） $\displaystyle R_{3,1}(r) = \left(\frac{Z}{a_0}\right)^{\frac{3}{2}} e^{-\rho_3(r) / 2} \cdot \frac{1}{9\sqrt{6}} (4 - \rho_3(r) ) \rho_3(r)$ 　（3p軌道） $\displaystyle R_{3,2}(r) = \left(\frac{Z}{a_0}\right)^{\frac{3}{2}} e^{-\rho_3(r) / 2} \cdot \frac{1}{9\sqrt{30}} (\rho_3(r) )^2$ 　（3d軌道）

思ったほど難しくはないなという気がしてきませんか？

なお、これは規格化定数の部分も計算した結果となっています。ここで、規格化定数の計算の仕方について説明します。

規格化定数を考える上では波動関数全体を考えた方がいいかもしれません。波動関数全体としては、三重積分

$\displaystyle \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} |\Psi_{n,l,m}(x,y,z)|^2 \, dx\,dy\,dz$

を計算した結果が $1$ になるというのが規格化の条件です。

今は、変数として球面座標系 $(r, \theta, \phi)$ を考えているので、変数変換して

$\displaystyle \int_{0}^{\infty} \int_{0}^{\pi} \int_{0}^{2\pi} |R_{n,l}(r)|^2 |Y_{l,m}(\theta, \phi)|^2 \, r^2 dr \sin\theta \,d\theta\, d\phi = 1$

が成り立つように規格化すれば良いでしょう。

変数を分離して

$\displaystyle \int_{0}^{\infty} |R_{n,l}(r)|^2 r^2 dr \cdot \int_{0}^{\pi} \int_{0}^{2\pi} |Y_{l,m}(\theta, \phi)|^2 \, \sin\theta \,d\theta \,d\phi = 1$

とします。

ここから、球面調和関数 $Y_{l,m}(\theta, \phi)$ は

$\displaystyle \int_{0}^{\pi} \int_{0}^{2\pi} |Y_{l,m}(\theta, \phi)|^2 \, \sin\theta \,d\theta \,d\phi = 1 \tag{7}$

によって規格化し、動径波動関数 $R(r)$ は

$\displaystyle \int_{0}^{\infty} |R_{n,l}(r)|^2 r^2 dr = 1 \tag{8}$

によって規格化すると考えるわけです。

本当のことを言うと、最終的に積をとった波動関数で定数の辻褄が合っていればよいわけで、どちらに規格化定数があっても大して問題はないのですが、こうしておくのが一般的だということですね。

式 $(8)$ の被積分関数を動径分布関数といいます。つまり、 $D(r) = r^2 |R_{n,l}(r)|^2$ というわけです。（これが前回私が動径波動関数と混同したものですね。）

半径 $r$ の球殻を考えたときに、その表面積は $4\pi r^2$ となります。したがって、半径 $r$ が大きくなればなるほど、電子がいる確率が高くなるわけです。それを加味した確率分布が $D(r)$ となっています。

$n = 1, \; l = 0$ のケースで、実際に規格化定数を求めてみましょう。

$\displaystyle R_{1,0}(r) = N_{1,0} e^{-\rho_n(r) / 2}$

とおいて、 $N_{1,0}$ を求めたいと思います。

積分

$\displaystyle \int R_{1,0}(r)^2 \,r^2\,dr$

を考えて、これが $1$ になるように $N_{1,0}$ を決めれば良いわけですね。

展開すると

$\displaystyle N_{1,0}^2 \int_{0}^{\infty} e^{-\rho_n(r)} \,r^2\,dr$

となるわけですが、これは高校の時にやった

$\displaystyle \int e^{-ax} \,x^2\,dx$

というタイプの積分ですね。

実際の計算はご自身でやっていただきたいですが、これは部分積分を繰り返し実行するタイプのものですね。あぁ、高校のときにやった積分は、こんなところでも役に立つのか。

計算すると

$\displaystyle \int e^{-ax} \,x^2\,dx = \frac{2}{a^3}$

となります。したがって、求めたかった積分は

$\displaystyle N_{1,0}^2 \int_{0}^{\infty} e^{-\rho_n(r)} \,r^2\,dr = N_{1,0}^2 \frac{a_0^3}{2^2 Z^3}$

となります。これが $1$ になるわけですから

$\displaystyle N_{1,0} = 2\left(\frac{Z}{a_0}\right)^{\frac{3}{2}}$

となって、係数がちゃんと求まるわけですね。

今考えた $n = 1, \; l = 0$ のケースは、1s軌道に相当する部分ですが、試しに $R(r)$ と $D(r)$ をグラフに書いてみましょう。とりあえず今回は水素原子を考えたいので、 $Z = 1$ としています。

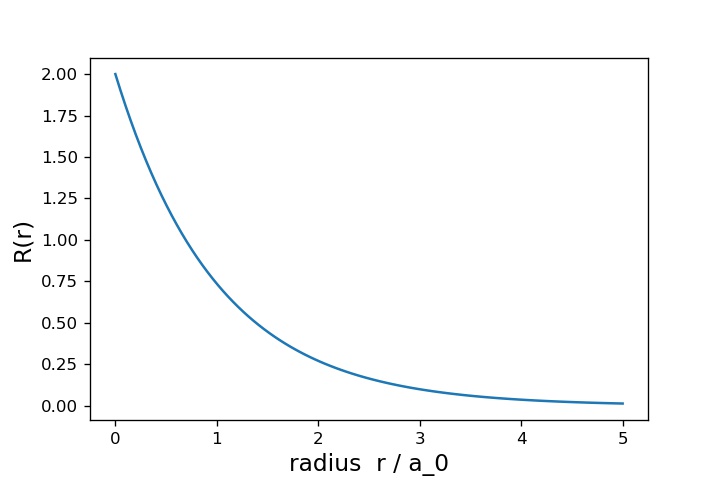
f:id:tsujimotter:20210704031208j:plain:w320

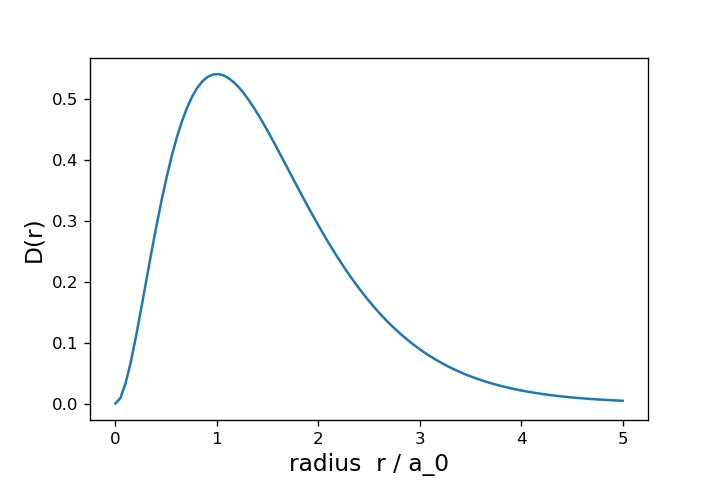
f:id:tsujimotter:20210704031224j:plain:w320

上が $R(r)$ で下が $D(r)$ です。横軸は $r/a_0$ として、縦軸でそれぞれの関数値を表示しています。

グラフを見ると、 $R(r)$ の方は原子核からの距離 $r$ が大きくなるほど、単調に小さくなっています。

一方、 $D(r)$ については、 $r$ が大きくなるほど球殻の面積自体は大きくなる効果があるので、それも加味して $r$ が小さいところでは確率が大きくなります。一方、 $r$
が十分大きい場合は、 $R(r)$ が指数的に小さくなる効果の方が強くなるので、単調に減少するようになります。結果的に、 $D(r)$ にピークができるわけですね。

$D(r)$ のピークの位置 $r$ を計算すると、実はこれがボーア半径 $a_0$ になっています。1s軌道にいる電子は、原子核からの距離がボーア半径の位置に最も多く分布するということになりそうです。ある意味では、これが水素原子における「1s軌道の大きさ」だと思うことができるでしょう。

これはあくまで「球殻全体の確率を寄せ集めたような確率分布を考えると、距離 $r$ がピークになる」と言っているに過ぎなくて、空間全体で見ると原点付近が最も高い確率で分布することになります。ややこしいですね。

ところで、電子の分布は大変小さいので、適切なスケールを設定しないと数値計算がすぐに破綻します。

そこで、何かしらのスケールの基準を考える必要が出てくるのですが、その基準としてボーア半径 $a_0$ が使えるのです。つまり、水素原子の1s軌道の大きさを基準に、そこからの相対的な大きさでものごとを測ることにするわけです。

実際にプログラムする上では、 $a_0 = 1$ とするだけでOKです。

これを踏まえて、動径波動関数とその描画部分を次のように実装します。

import numpy as np
import matplotlib.pyplot as plt

# 動径波動関数（ボーア半径を a_0 = 1 になるようなスケールを考える）
def radial_wave_function(r, n, l):
    Z = 1        # 水素原始を想定しているので Z = 1
    rho = 2.0 * Z * r / n
    if n == 1 and l == 0:
        return (Z ** 1.5) * np.exp(-rho/2.0) * 2.0
    elif n == 2 and l == 0:
        return (Z ** 1.5) * np.exp(-rho/2.0) * (2.0 - rho) / (2.0*np.sqrt(2.0))
    elif n == 2 and l == 1:
        return (Z ** 1.5) * np.exp(-rho/2.0) * rho / (2.0*np.sqrt(6.0))
    elif n == 3 and l == 0:
        return (Z ** 1.5) * np.exp(-rho/2.0) * (6.0 - 6.0*rho + rho**2) / (9.0*np.sqrt(3.0))
    elif n == 3 and l == 1:
        return (Z ** 1.5) * np.exp(-rho/2.0) * (4.0 - rho) * rho / (9.0*np.sqrt(6.0))
    elif n == 3 and l == 2:
        return (Z ** 1.5) * np.exp(-rho/2.0) * (rho**2) / (9.0*np.sqrt(30.0))
    
    
# 量子数の設定
n = 1
l = 0

# グラフの描画部分
r = np.linspace(0, 5, 100)

plt.figure()
plt.plot(r, radial_wave_function(r, n, l))  # 動径波動関数
plt.xlabel("radius  r / a_0", fontsize=14)
plt.ylabel("R(r)", fontsize=14)
plt.savefig("R_r_1s.jpg", dpi=120)
plt.show()

plt.figure()
plt.plot(r, (radial_wave_function(r, n, l)**2) * (r**2))  # 動径分布関数
plt.xlabel("radius  r / a_0", fontsize=14)
plt.ylabel("D(r)", fontsize=14)
plt.savefig("D_r_1s.jpg", dpi=120)
plt.show()

2. 三次元空間における電子雲をいかに計算するか？

さて、動径波動関数が計算できたので、本題の電子雲の計算です。

波動関数は

$\Psi_{n,l,m}(x, y, z) = R_{n,l}(r)\, Y_{l,m}(\theta, \phi)$

となり、後ろの二つの関数は既に計算できていますので、あとは

$|\Psi_{n,l,m}(x, y, z)|^2$

を計算するだけだと思うかもしれません。ところが、これを可視化するというのは、それほど簡単なことではありません。

というのも、変数自体が $(x, y, z)$ の３変数であり、結果の確率密度関数は１変数だと考えると、描画のためには４次元必要です。我々の頭はせいぜい３次元しか認識できないので、そのまま可視化するのは難しそうです。

方法１：次元を落とす

どうしたらよいでしょうか。1つの方法として、1次元情報を落とすという手があるでしょう。

実際、 $z = 0$ の平面だけを考えて、その上にある電子 $(x, y, 0)$ の確率密度関数 $|\Psi(x, y, 0)|^2$ を３次元でプロットすることができます。

たとえば、2p軌道（x軸方向）をプロットしてみるとこうなります：

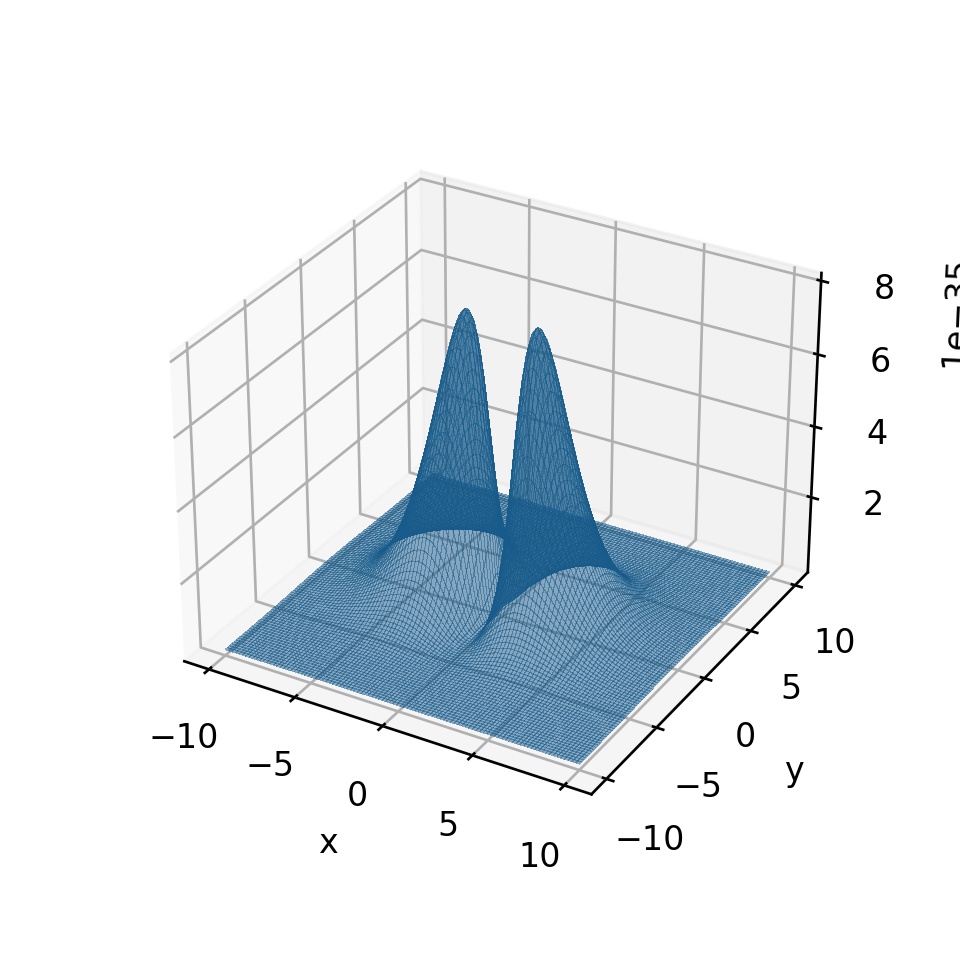
f:id:tsujimotter:20210704032501j:plain:w340

これも使えないことはないのですが、 $z \neq 0$ の様子は分かりませんし、どうも味気ないですね。もう少し空間的な分布の情報が知りたいですね。

方法２：散布図としてプロット

もう一つの方法は、３次元の散布図としてプロットするという方法です。

電子は確率分布 $|\Psi(x, y, z)|^2$ に従って、ランダムに空間上に存在しています。この確率分布で電子をサンプリングして、それを散布図にプロットすれば良いわけですね。

しかし、この方法には一つ大きな問題があります。この方法にトライするためには、 $|\Psi(x, y, z)|^2$ に従う乱数を生成する必要があります。 $|\Psi(x, y, z)|^2$ なんていう「ヘンテコな確率分布」に従う乱数なんて、どうやって生成することができるのでしょう？

方法はないわけではありません。たとえば、棄却サンプリングという方法があります。

サンプルを生成したいターゲット分布（今回であれば、 $|\Psi(x, y, z)|^2$ ）を覆うような、別の確率分布（たとえば、一様乱数）を考えます。後者から生成されたサンプル $y$ を用いて、両者の分布の比を元に、サンプル $y$ を採用するか棄却するか決める。この方法によりターゲット分布を再現する乱数を生成する方法です。詳しい方法を説明するのは難しいので、どこかのサイトをご覧いただきたいと思います。

実際、棄却サンプリングによって得られた結果は次のようになります：

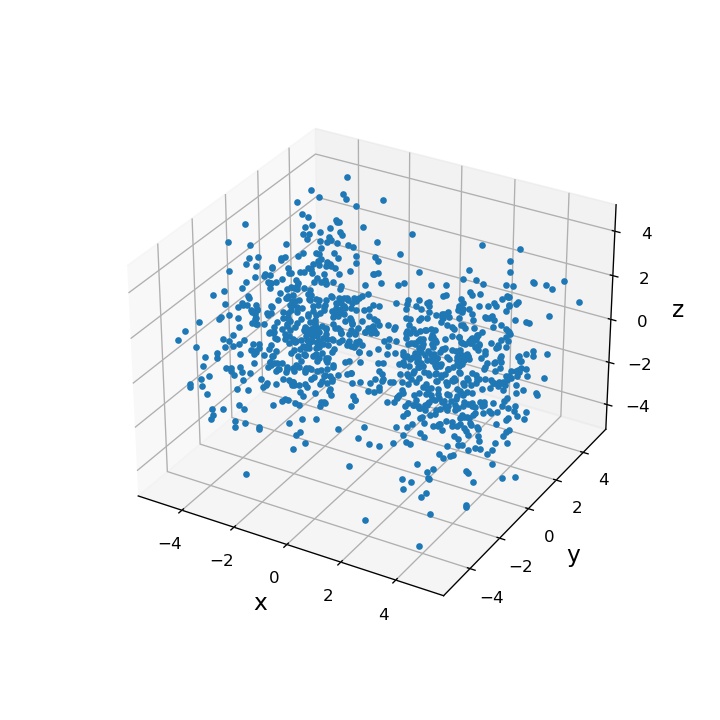
f:id:tsujimotter:20210704031955j:plain:w400

なかなかいい感じに見えますね！　これは2p軌道の（特に $x$ 方向のもの）をサンプリングしたのですが、 $x$ 方向に「マラカスのような図形」があって、その周りに電子が局在していることがよくわかると思います。

この方法、一見よい感じに見えるのですが、時間がかかり過ぎるという難点があります。というのも、ターゲット分布（今回は $|\Psi(x, y, z)|^2$ ）と、サンプル生成に使う分布（今回は一様分布）が似ていれば問題ないのですが、両者の分布が遠ければ遠いほど、棄却する確率が上ってしまうからです。

私のプログラムはあまり洗練されたプログラムではないですが、上記の結果（1000サンプル）を出すのに１時間近くかかってしまいました。あまりに遅いので、C言語のプログラムに書き直したのですが、それでもこれぐらいかかってしまいました。

棄却サンプリングのような素朴な方法では、上記のような問題によってうまくいかないことが多いです。

そこでもう少し洗練されたサンプリング方法が提案されています。有名なものだと、マルコフ連鎖モンテカルロ法（MCMC法）というものがあります。

しかしながら、私はこういう方法に精通していないので、今回はチャレンジしませんでした。いつか理解できればと思っています。

追記（2021.07.24）：
・・・と書いていたのですが、マルコフ連鎖モンテカルロ法の一種であるメトロポリス・ヘイスティングス法が、思いの外簡単に実装できました。

せっかくなので、こちらに記事にしていますので、この方法に興味をお持ちの方はご覧になってください：
tsujimotter.hatenablog.com

方法３：確率90%となるような領域を可視化

そんなわけで、第３の方法を考えたいと思います。それが「確率90%となるような領域を可視化する」という方法です。

たとえば教科書にあるようなs軌道とかp軌道の図は、この方法によって可視化されているようです。

この方法は「おそらく」以下のような方法だと思います。

まず確率密度関数 $|\Psi(x, y, z)|^2$ のピークの値 $P = P_{MAX}$ を探します。この $P_{MAX}$ からスタートして、 $P$ を少しずつ小さくしていくのです。

$P$ に対応して、 $|\Psi(x, y, z)|^2 < P$ を満たす $(x, y, z)$ 全体の領域 $A(P)$ を考えます。この $A(P)$ 上で積分 $I(P) = \int_{A(P)} |\Psi(x, y, z)|^2 dxdydz$ を考えます。

$I(P) \geq 0.9$ を満たす最大の $P$ を求めて、このときの $A(P)$ を可視化してあげれば良いというわけです。

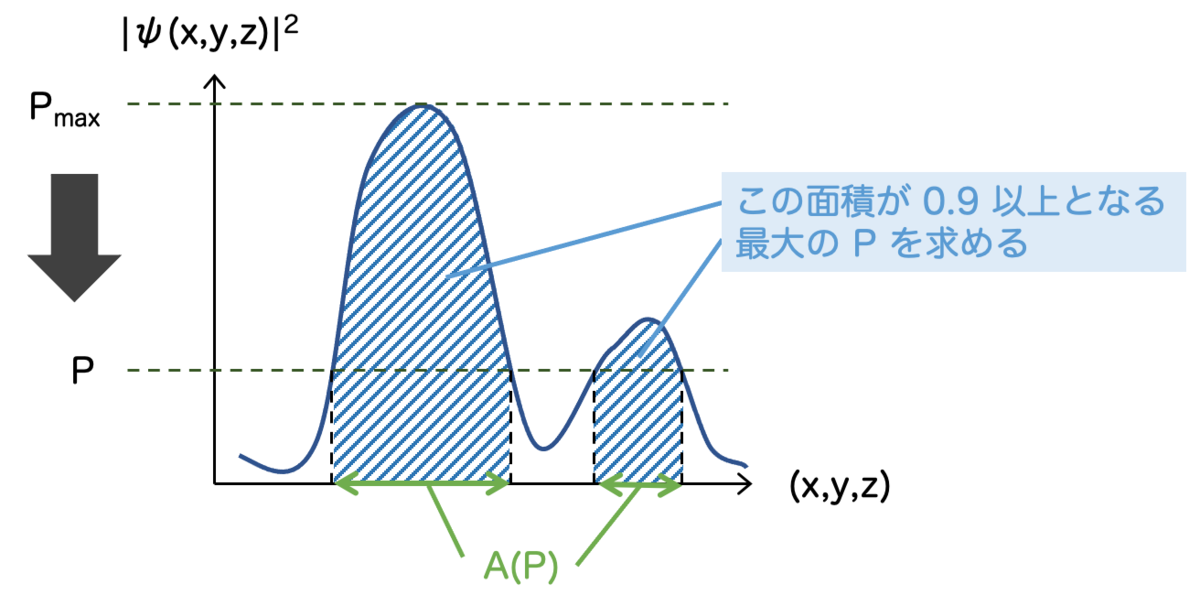
f:id:tsujimotter:20210704201616p:plain:w500

私をこの方法を考えているときにルベーグ積分を思い浮かべました。

リーマン積分は縦に切る、ルベーグ積分は横に切るとよく言いますが、上記はまさにルベーグ積分的な計算を実行しているわけです。

難しく聞こえるかもしれませんが、アイデアは直感的です。確率密度関数を上下ひっくり返して水浸しにしていき、全体の90%が注がれた段階でストップします。水が入っている領域を可視化する、それだけです。

私は今、まるで「上記の方法が一般によく知られている」かのように説明しました。しかしながら、実際は私のオリジナルの方法です。

正確に言えば、「確率90%となるような領域を可視化する」というアイデアはありました。アイデアだけは色々なところで聞くのですが、実際にどうやって実装したら良いか書かれたものを私は見たことがありません。

「みんな簡単に90%っていうけど、実際どうやって可視化したらええんや」

そんな風にひとしきり悩んだ結果、上の方法を思いついたに過ぎません。そのため、これが正当な方法ではないかもしれません。とりあえず、この方法でやってみたらそこそこうまくいきましたので、今回はこの方法でいきたいと思います。

上の説明で

「 $A(P)$ 上で積分 $I(P) = \int_{A(P)} |\Psi(x, y, z)|^2 dxdydz$ を考えます」

と書いた部分が、いかにも難しそうだと思った方もいるかもしれません。私も実装する前は、ここが一番難しそうだと考えていました。

私の解決方法は、空間をグリッド状に離散化することです。体積が $\Delta V = \Delta x \Delta y \Delta z$ であるような均等なグリッドによって空間を分割し、各グリッドに番号をつけます。

番号 $i$ のグリッドを代表する座標を $(x_i, y_i, z_i)$ とし、その点上の確率密度関数 $|\Psi(x_i, y_i, z_i)|^2$ を計算します。

すると、電子がグリッド $i$ に存在する確率は

$\displaystyle P_i = |\Psi(x_i, y_i, z_i)|^2 \Delta V$

と表せるわけです。あくまで近似的には。

あとは、各グリッドの存在確率 $P_i$ を並べたリストを用意して、降順にソートします。上から順にグリッドの確率を足し合わせていき、合計が $0.9$ 以上になるまで続けます。

終了した時点で、確率を足し合わせるのに使ったグリッドを、すべて描画してあげれば良いわけですね。グリッドを描画するので少しカクツクかもしれませんが、十分に $\Delta V$ を小さく取れば、それなりには綺麗に見えそうです。

そんなわけで、上記の方針によって、水素原子の電子雲を描画したのが次の図です。

f:id:tsujimotter:20210704033602j:plain:w300

1s軌道 $(n,l,m) = (1,0,0)$

f:id:tsujimotter:20210704033628j:plain:w300

2s軌道 $(n,l,m) = (2,0,0)$

f:id:tsujimotter:20210704033647j:plain:w300

$2p_z$ 軌道 $(n,l,m) = (2,1,0)$

f:id:tsujimotter:20210704033725j:plain:w300

$2p_y$ 軌道 $(n,l,m) = (2,1,-1)$

f:id:tsujimotter:20210704033710j:plain:w300

$2p_x$ 軌道 $(n,l,m) = (2,1, 1)$

プログラムは以下の通りです。プログラム内の量子数を適当にいじってあげれば、いろいろな軌道が見れますので、遊んでみてください。

# 「90%サンプリング法」による水素原子の軌道（電子雲）の可視化

import numpy as np
import matplotlib.pyplot as plt
import mpl_toolkits.mplot3d.axes3d as axes3d

import math


# 動径波動関数（ボーア半径を a_0 = 1 に正規化）
def radial_wave_function(r, n, l):
    Z = 1        # 水素原始を想定しているので Z = 1
    rho = 2.0 * Z * r / n
    if n == 1 and l == 0:
        return (Z ** 1.5) * np.exp(-rho/2.0) * 2.0
    elif n == 2 and l == 0:
        return (Z ** 1.5) * np.exp(-rho/2.0) * (2.0 - rho) / (2.0*np.sqrt(2.0))
    elif n == 2 and l == 1:
        return (Z ** 1.5) * np.exp(-rho/2.0) * rho / (2.0*np.sqrt(6.0))
    elif n == 3 and l == 0:
        return (Z ** 1.5) * np.exp(-rho/2.0) * (6.0 - 6.0*rho + rho**2) / (9.0*np.sqrt(3.0))
    elif n == 3 and l == 1:
        return (Z ** 1.5) * np.exp(-rho/2.0) * (4.0 - rho) * rho / (9.0*np.sqrt(6.0))
    elif n == 3 and l == 2:
        return (Z ** 1.5) * np.exp(-rho/2.0) * (rho**2) / (9.0*np.sqrt(30.0))

# 球面調和関数（ただし、実関数表示したもの）
def spherical_harmonics(theta, phi, l, m):
    if l == 0:
        if m == 0:
            # l=0, m=0
            return np.sqrt(1.0/(4*np.pi))
    if l == 1:
        if m == 0:
            # l=1, m=0
            return np.sqrt(3.0/(4.0*np.pi)) * np.cos(theta)
        if m == 1:
            # l=1, m=+1
            return np.sqrt(3.0/(4.0*np.pi)) * np.sin(theta) * np.cos(phi)
        if m == -1:
            # l=1, m=+1
            return np.sqrt(3.0/(4.0*np.pi)) * np.sin(theta) * np.sin(phi)
    if l == 2:
        if m == 0:
            return np.sqrt(5.0/(16.0*np.pi)) * (3.0*(np.cos(theta)**2) - 1.0)
        if m == 1:
            return np.sqrt(15.0/(4.0*np.pi)) * np.cos(theta) * np.sin(theta) * np.cos(phi)
        if m == -1:
            return np.sqrt(15.0/(4.0*np.pi)) * np.cos(theta) * np.sin(theta) * np.sin(phi)
        if m == 2:
            return np.sqrt(15.0/(16.0*np.pi)) * (np.sin(theta)**2) * np.cos(2*phi)
        if m == -2:
            return np.sqrt(15.0/(16.0*np.pi)) * (np.sin(theta)**2) * np.sin(2*phi)

        
# 水素原子の波動関数 Ψ_{n,l,m}(x, y, z)
def f(x, y, z, n, l, m):
    # 座標系を (x,y,z) -> (r,θ,φ) に変換
    r = np.sqrt(x*x + y*y + z*z)
    
    theta = 0.0
    phi = 0.0
    if r > 0:
        theta = np.arccos( z / r )
    if y == 0:
        if x < 0:
            phi = np.pi
    elif x*x+y*y > 0:
        phi = np.sign(y) * np.arccos(x/np.sqrt(x*x+y*y))
        
    # 動径波動関数と球面調和関数の積を計算して出力
    return (radial_wave_function(r, n, l) * spherical_harmonics(theta, phi, l, m))




# 量子数（好きな量子数を選んでください）
n = 2
l = 1
m = 0


# サンプリングの設定
N = 30                    # サンプリング数（x,y,zをそれぞれ N 等分する）
x_range = 10              # 計算したい全体領域の範囲 (-x_range <= x,y,z <= x_range)
delta = 2.0*x_range / N   # サンプリング間隔


# 3次元空間を格子状にして、各グリッドの確率密度関数をサンプリング（間隔 delta, グリッド数 N^3 個）
data_list = []
for i in range(N):
    for j in range(N):
        for k in range(N):
            # 各グリッドの点 (x,y,z) を計算
            x = i*delta - x_range
            y = j*delta - x_range
            z = k*delta - x_range
            
            # グリッドの代表点の座標 (x,y,z) における波動関数 Ψ(x,y,z) を計算
            psi = f(x,y,z,n,l,m)
            
            # 波動関数の2乗によって電子の確率密度関数 |Ψ(x,y,z)|^2 を計算
            pdf = psi**2
            
            # 確率密度(|Ψ(x,y,z)|^2, p.d.f), x, y, z, 波動関数の生の値 Ψ(x,y,z) の順にデータを格納
            data_list.append([pdf, x, y, z, psi])


# 確率密度が高い順にグリッドをソートする
sorted_list = sorted(data_list, key=lambda data: data[0], reverse=True)  # 確率密度(p.d.f)でソート



# 波動関数が正のデータを格納する変数
x1_list = []
y1_list = []
z1_list = []

# 波動関数が負のデータを格納する変数
x2_list = []
y2_list = []
z2_list = []


# |Ψ|^2 ΔV の総和( total )が 0.9 以上になるまで足し合わせる（totalが0.9以上になったらwhileを抜ける）
total = 0.0
i = 0
while total < 0.9:
    pdf = sorted_list[i][0]  # 確率密度関数 |Ψ(x,y,z)|^2
    x = sorted_list[i][1]
    y = sorted_list[i][2]
    z = sorted_list[i][3]
    psi = sorted_list[i][4]
    
    # 現在考えているグリッドの |Ψ(x,y,z)|^2 ΔV の計算
    grid_probability = pdf * delta**3
    total += grid_probability
    
    if psi > 0:
        x1_list.append(x)
        y1_list.append(y)
        z1_list.append(z)
    else:
        x2_list.append(x)
        y2_list.append(y)
        z2_list.append(z)   
    i += 1


# データを ndarray に変換
X1 = np.array(x1_list)
Y1 = np.array(y1_list)
Z1 = np.array(z1_list)

X2 = np.array(x2_list)
Y2 = np.array(y2_list)
Z2 = np.array(z2_list)


# figureを生成する
fig = plt.figure(figsize=(8.0, 8.0))
ax = fig.add_subplot(1,1,1, projection='3d')

ax.set_xlim3d(-x_range, x_range)
ax.set_ylim3d(-x_range, x_range)
ax.set_zlim3d(-x_range, x_range)

# 軸の設定
ax.set_xlabel("x", size = 14)
ax.set_ylabel("y", size = 14)
ax.set_zlabel("z", size = 14)

ax.plot(X2,Y2,Z2,color='b',marker="o",linestyle='None')
ax.plot(X1,Y1,Z1,color='r',marker="o",linestyle='None')

plt.show()

注意点がいくつかあるので補足します。

ボーア半径 $a_0$ が $a_0 = 1$ になるように、各座標のスケールをとっている。すなわち、図の "1" という大きさは "1 ボーア半径"（つまり 52.9 [pm]）。

分布を計算するときには、デカルト座標に対する波動関数 $\Psi(x,y,z)$ を計算する必要があるが、実際は $(x, y, z) \mapsto (r, \theta, \phi)$ と変換する必要がある（プログラム内の $f(x,y,z,n,l,m)$ 関数の実装部分）。このときの変換は次のように行う：

$\begin{cases} r = \sqrt{x^2 + y^2 + z^2} \\ \theta = \arccos \frac{z}{\sqrt{x^2+y^2+z^2}} \\ \phi = \text{sign}(y) \, \arccos \frac{x}{\sqrt{x^2+y^2}}\end{cases}$

ここで、 $\text{sign}(y)$ は $y > 0$ のとき $1$ 、 $y < 0$ のとき $-1$ を返す関数
ただし、 $x,y,z$ が $0$ になるとき想定外の挙動が発生する場合があるので、適切に場合分けして処理する必要がある。

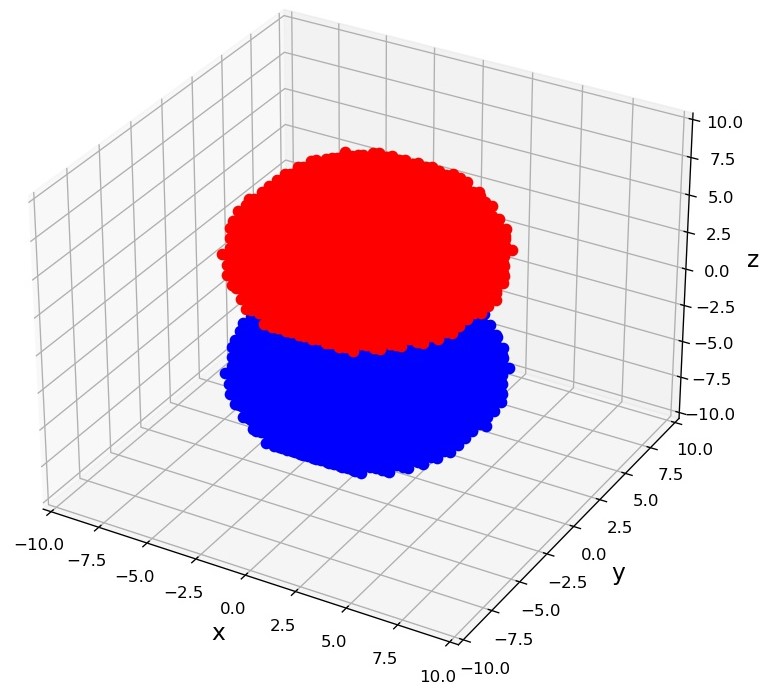
色分けについて。赤色が波動関数 $\Psi(x,y,z)$ の（絶対値を取る前の）値が正（赤色）か負（青色）かで色分けしている。

matplotlibの仕様上、後から書いたプロット点が、図の上のレイヤーに来るようにプロットされてしまう（下図のように）。したがって、 $p_z$ 軌道を $z$ 軸の下側から眺める、青ではなく赤い方が手前に来るように見える。これは大変不自然な挙動であるが、matplotlibの仕様なので諦めてほしい。（さもなくば、違うプロットツールを使う。）

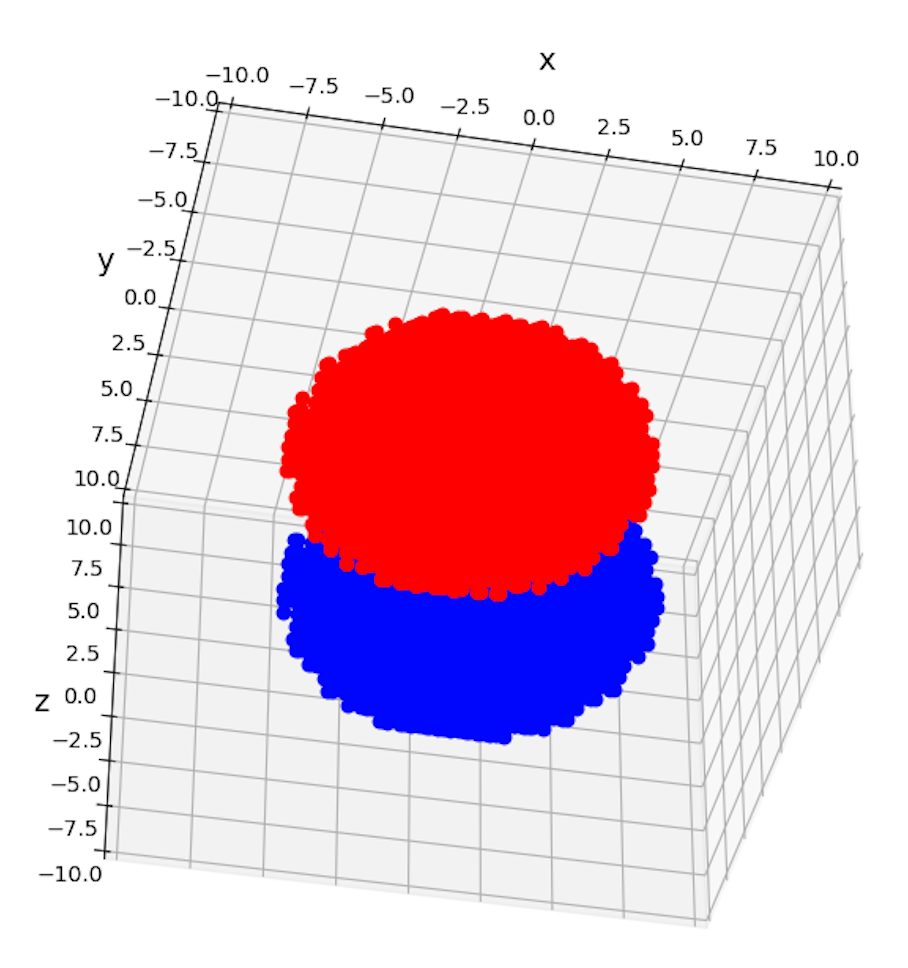
f:id:tsujimotter:20210704143308p:plain:w260

このプログラムに至るまでにかなり試行錯誤をしたのですが、おかげで思った通りの図が作れてとても楽しいです。

3. 補足：有効核電荷とスレーター則

ここまでは、水素原子の軌道を考えてきたので、原子核の電荷としては $Z = 1$ だけを考えればよかったのでした。

より大きな原子核を扱う場合は、 $Z$ を陽子の個数（つまり原子番号）に変えてあげればよいでしょう。有機化学でよく使う炭素原子 ${}_6C$ については、 $Z = 6$ とすればよいわけです。

ここで $Z$ の値を変えたときに影響が出るのは、動径波動関数 $R(r)$ です。実際、1s軌道において $Z$ を大きくしていくと、以下の図のように電子のサイズが変わります：

f:id:tsujimotter:20210704123434j:plain:w600

$Z$ が大きくなるにつれて電子軌道が小さくなることが観察できますね。物理的には、原子核のクーロン力が強くなるので、電子がより原子核に引き寄せられるようになるから、と解釈ができます。

$Z$ によって大きさがかなり違うので、化学結合を考える際にはこの辺をきちんと考慮する必要が出てきそうです。

もう一つ、水素以外の原子を考えるときに気をつける必要があるのは、他の電子の影響です。

たとえば、炭素を考えるときには、1s軌道に2個、2s・2p軌道に4個で、計6個の電子があります。これらが互いに相互作用する影響を踏まえる必要があるわけです。

2p軌道にある電子からすると、その内側に1s軌道の電子があり、クーロン力による斥力が働きます。この効果は、原子核によって引き寄せられる力を弱める方向に働くと考えられます。

一般に、多電子原子（電子が１個以上の原子）を考えるときには、シュレーディンガー方程式を厳密に解くのは難しいです。その代わりに、多電子の影響を原子核電荷 $Z$ に押し付けるという方法があります。 $Z$ を

$Z_{\text{eff}} = Z - \sigma$

のように補正することで、電子の斥力が原子核の引力を弱めていると考えるわけですね。 $Z_{\text{eff}}$ のことを有効核電荷といい、 $\sigma$ を遮蔽定数といいます。遮蔽定数は正の値を取ります。

遮蔽定数 $\sigma$ はどうやって決めるのかということですが、基本的には実験的に決めていくしかないでしょう。しかしながら、経験的にうまくいく計算法則があります。それがスレーター則です。

スレーター則では、まず軌道を以下のようにグループ分けします。

グループ	1	2	3	4
軌道	1s	2s, 2p	3s, 3p	3d

炭素原子における2p軌道の電子からすると、内側のグループにある電子は1sの2個だけなので、その効果は1個につき $0.85$ だと考えます。また、同じグループの残りの電子は $2s, 2p$ の3個であり、この影響は1個につき $0.35$ です。よって、 $\sigma$ は

$\sigma = 2\times 0.85 + 3\times 0.35 = 1.7 + 1.05 = 2.75$

と計算されます。したがって、炭素原子における2p軌道の電子についての有効核電荷は

$Z_{\text{eff}} = Z - \sigma = 6 - 2.75 = 3.25$

と計算されるわけですね。結構大きな影響になりますね。

プログラムに反映させると、次のようになります。

# 動径波動関数（ボーア半径を a_0 = 1 になるようなスケールを考える、有効核電荷を考慮）
def radial_wave_function(r, n, l):
    Z = 6        # 炭素原子を考える
    Z_eff = Z - (2 * 0.85 + 3 * 0.35)   # 2p電子の有効核電荷をスレーター則で求める
    rho = 2.0 * Z_eff * r / n
    if n == 1 and l == 0:
        return (Z_eff ** 1.5) * np.exp(-rho/2.0) * 2.0
    elif n == 2 and l == 0:
        return (Z_eff ** 1.5) * np.exp(-rho/2.0) * (2.0 - rho) / (2.0*np.sqrt(2.0))
    elif n == 2 and l == 1:
        return (Z_eff ** 1.5) * np.exp(-rho/2.0) * rho / (2.0*np.sqrt(6.0))
    elif n == 3 and l == 0:
        return (Z_eff ** 1.5) * np.exp(-rho/2.0) * (6.0 - 6.0*rho + rho**2) / (9.0*np.sqrt(3.0))
    elif n == 3 and l == 1:
        return (Z_eff ** 1.5) * np.exp(-rho/2.0) * (4.0 - rho) * rho / (9.0*np.sqrt(6.0))
    elif n == 3 and l == 2:
        return (Z_eff ** 1.5) * np.exp(-rho/2.0) * (rho**2) / (9.0*np.sqrt(30.0))

注意したいのは、 $Z_{\text{eff}}$ は各電子ごとに個別に計算する必要があるということです。すなわち、 $1s$ 軌道の電子を計算するときは、また別の計算をする必要があるということですね。

なお、今は炭素原子の2p軌道についてのみ計算しましたが、スレーター則の一般的な計算方法についてはここでは紹介しません。
（このシリーズの記事では炭素しか扱わない予定なので、炭素原子以外は計算する必要がありません。）

結構細かいルールがあってややこしいのですが、興味がある方は調べてみてください。参考文献の本にも載っています。

次回予告

ここまで水素原子などの１つの原子を扱ってきました。

次回はいよいよ、分子を扱いたいと思います。今回の記事はそのための布石でした。分子の電子軌道は、いったいどうやったら計算できるのか。σ結合・π結合とは何なのか。

そういった話をできればと思っています。お楽しみに！

参考文献

量子化学　基礎から応用まで

作者:金折賢二
講談社

Amazon

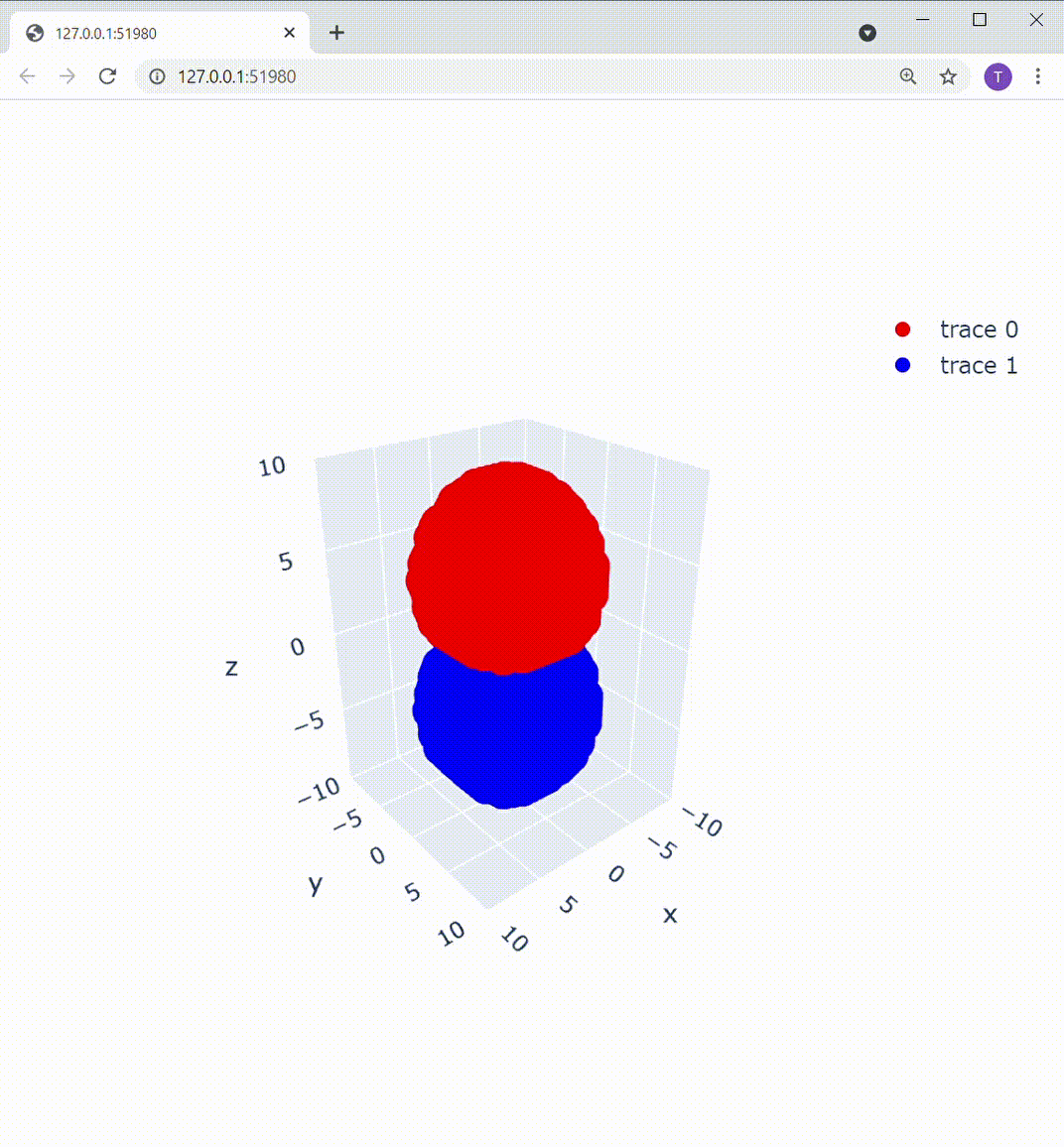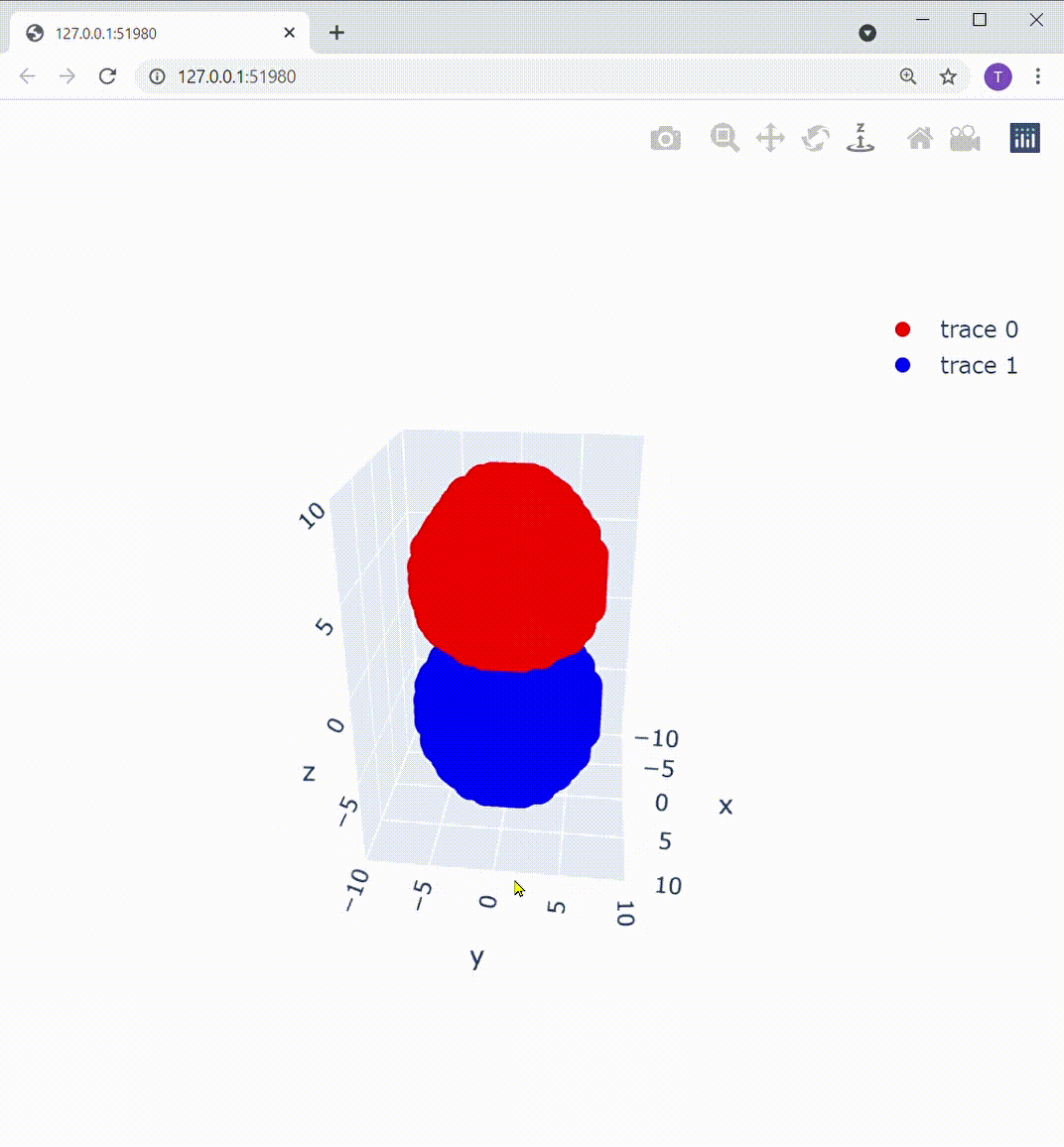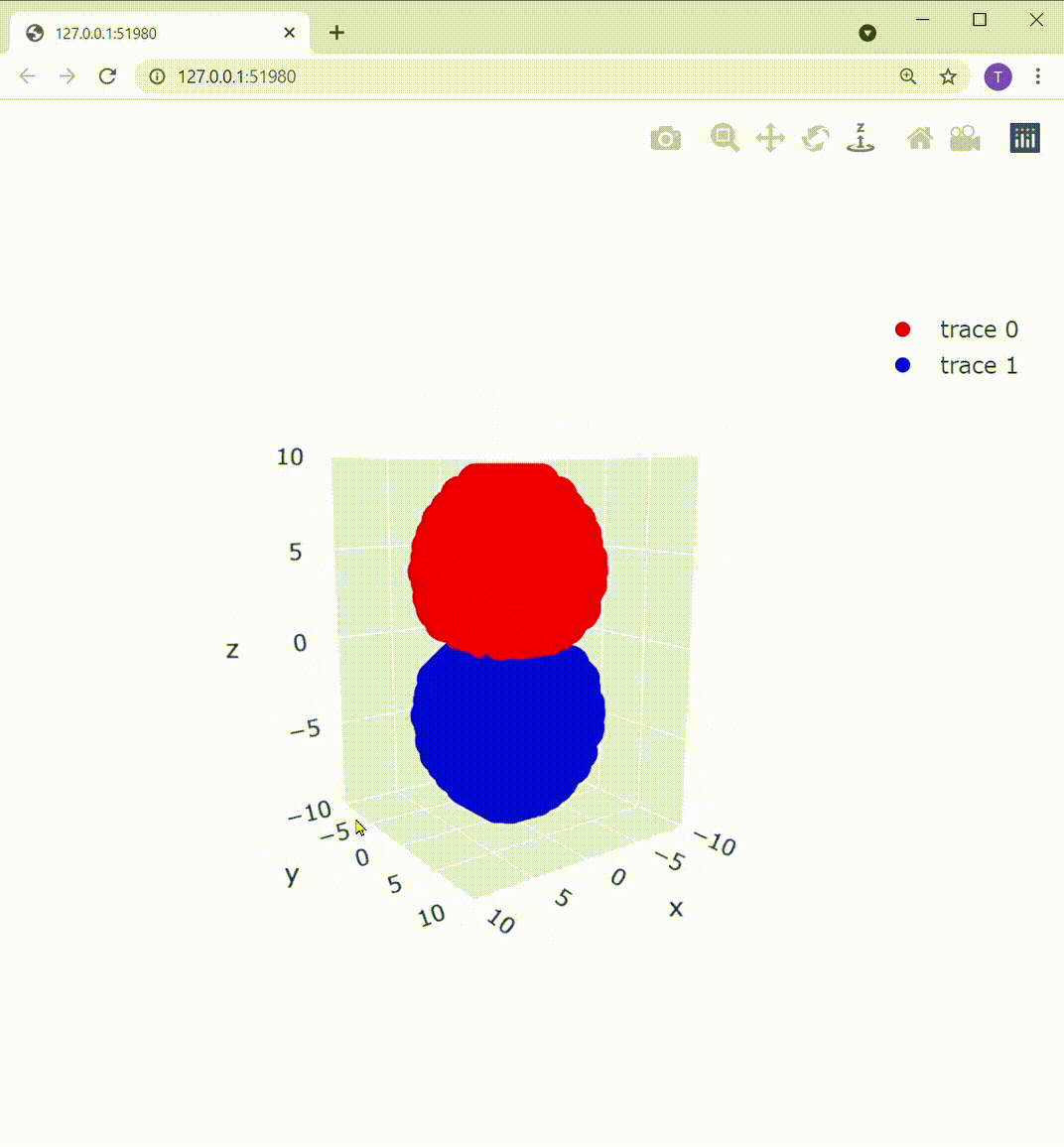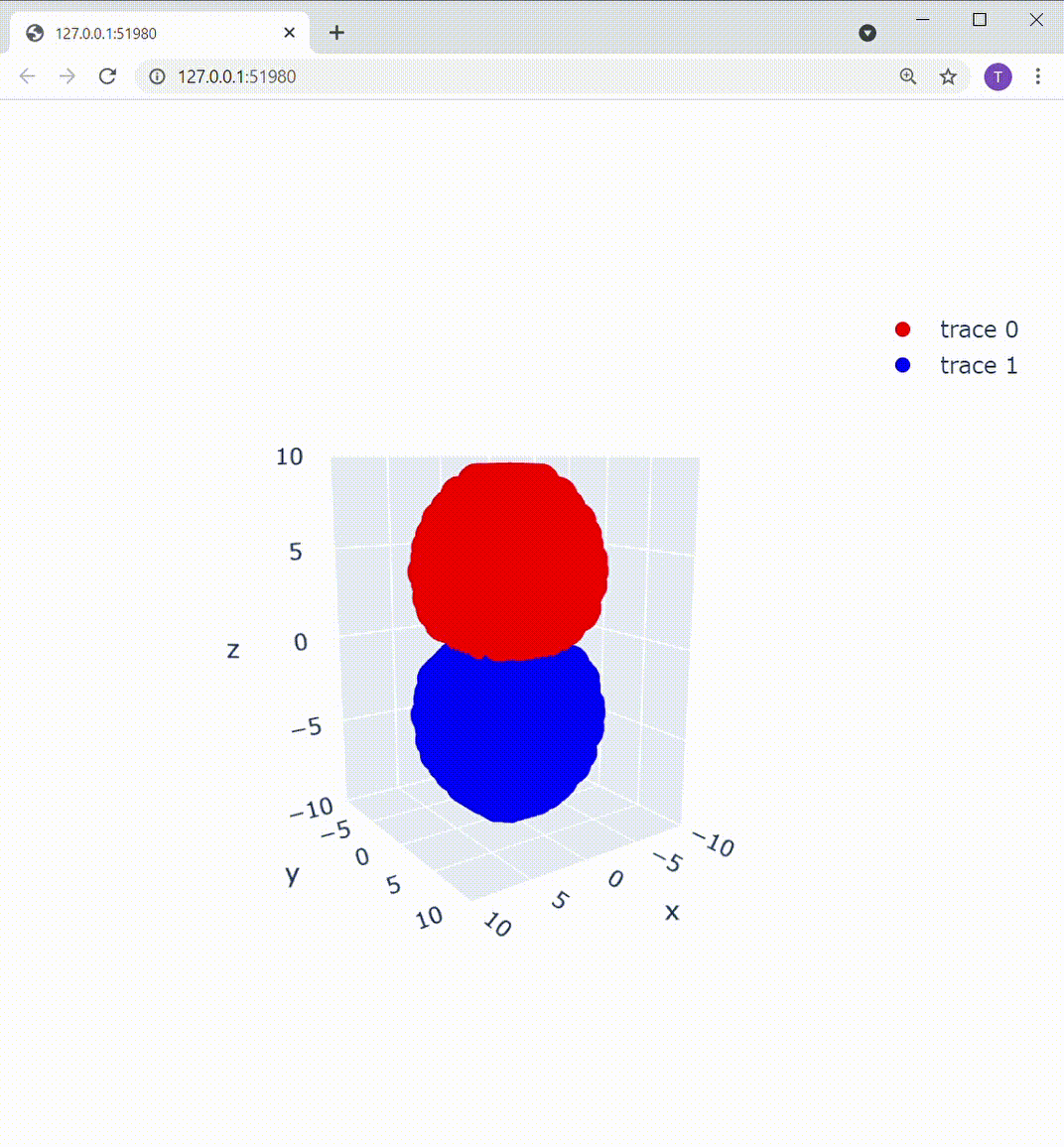
追記（Plotlyを使用した可視化）：

matplotlibのUIの不満を書いていたら、いちかわけんとさん（ @kentosho ）よりPlotlyというおしゃれなツールをご紹介いただきました。早速使ってみたのですが、これ非常にいいですね！

これによって描画部分を置き換えてあげると、こうなります：

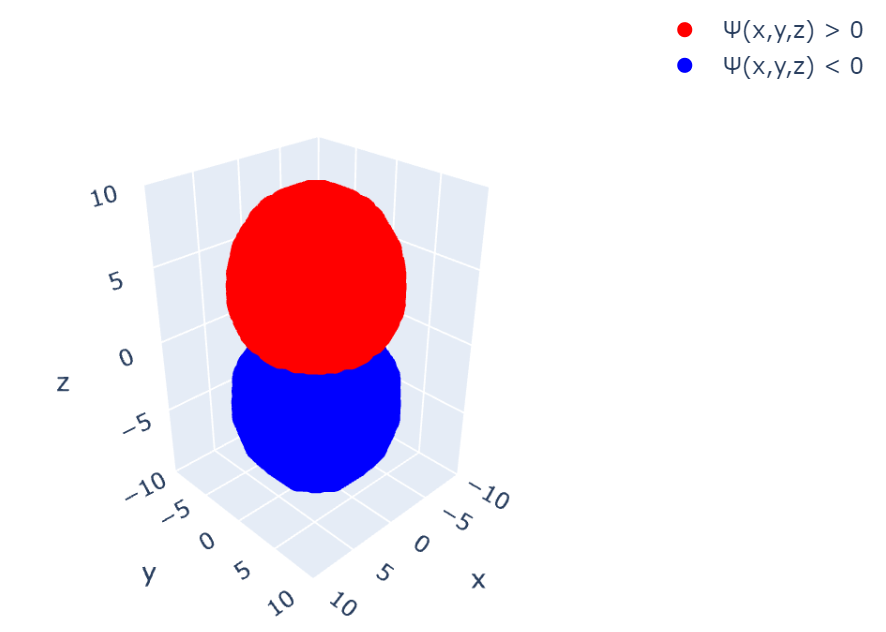
f:id:tsujimotter:20210704183903p:plain:w300

Z軸の下方向から見ても、この通り：

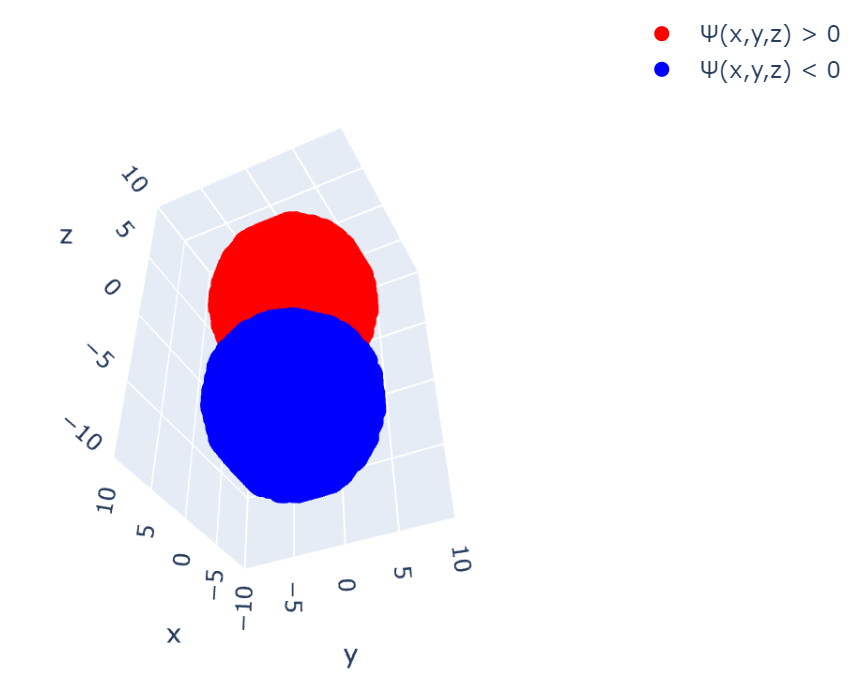
f:id:tsujimotter:20210704183941p:plain:w300

描画の部分を以下のコードに置き換えてあげれば動くと思います。
（ただし、事前にPlotlyをインストールしておく必要があります。普通のPythonを使っている方はpipで、Anacondaを使っている方はcondaでインストールしてみてください。）

import plotly.graph_objects as go

fig = go.Figure(data=[go.Scatter3d(
    x = X1,
    y = Y1,
    z = Z1,
    mode='markers',
    marker_color='red',
    name="Ψ(x,y,z) > 0",
), go.Scatter3d(
    x = X2,
    y = Y2,
    z = Z2,
    mode='markers',
    marker_color='blue',
    name="Ψ(x,y,z) < 0",
)])

fig.update_layout(
    scene = dict(
        xaxis = dict(range=[-x_range, x_range]),
        yaxis = dict(range=[-x_range, x_range]),
        zaxis = dict(range=[-x_range, x_range]),
    )
)

fig.show()