先日、ロマンティック数学ナイトオンライン(以下、ロマ数)というイベントに出演しました。
wakara.co.jp
そのイベントの報告はまたいずれしたいと思いますが、今日はそのイベントで竹内英人先生(以下、たけちゃん先生)がされた発表についてのお話です。
たけちゃん先生の話を聞いているうちに、問題を拡張したら面白くなるのでは、というアイデアが浮かんできて、それについて考えているうちに面白くなってしまいました。今日はそのことについて紹介したいと思います。
実は、今回の内容は、本日まさに今開催の 第18回日曜数学会 で発表する内容となっています。よろしければ、発表と一緒にお楽しみください。
live2.nicovideo.jp
たけちゃん先生の問題(オリジナル)
整数係数の2次の多項式 があります。
たとえば、 などを考えましょう。これを因数分解すると、
となります。
左辺から右辺へと変形するには、いわゆる 「たすきがけ」 をするのが一般的ですね。
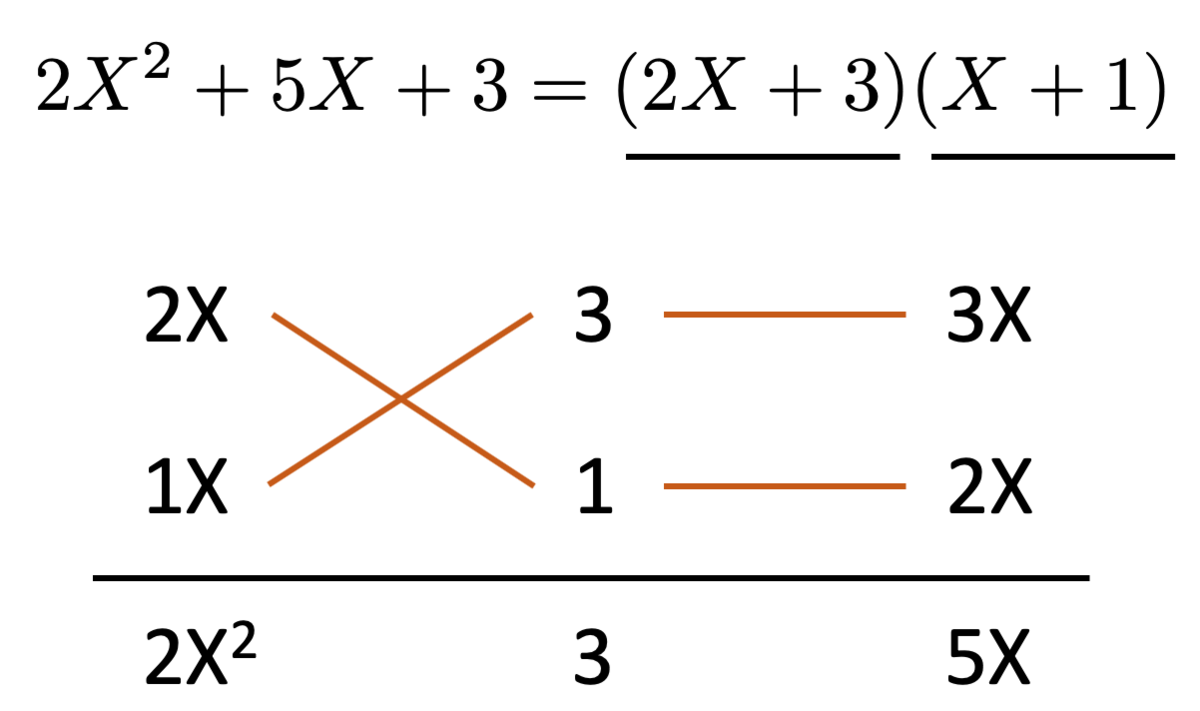
これが正しいことを確認するには、右辺を展開して左辺に一致することを見ればよいでしょう。
さて、右辺の式は1次の多項式の積になっていますが、どちらも 係数は整数 となっています。このように、係数が整数となるような多項式の積に分解できるとき、整数係数の範囲で因数分解できる ということにします。
という分解になるわけですが、どうやっても係数は複素数になってしまい、整数係数の範囲で分解することはできません。
たけちゃん先生は、一歩進んで、係数 の順番を入れ替えたときに、同様に整数係数の範囲で分解できるかという点についても言及していました。
たとえば、先ほどの例 では
ですが、
を入れ替えた多項式
も
となり、同様に整数係数の範囲で分解できます。
一般に
が成り立ちます。
つまり が整数係数の範囲で分解できるかどうかは、係数
を入れ替えても変わらない、ということですね。
この事実はあとで使うので覚えておいてください。
多項式が整数係数の範囲で分解できる条件について、tsujimotterはこれまでちゃんと考えたことがなかったので、新しい視点が得られてとても面白かったです。
tsujimotterの問題
さて、ここからはtsujimotterのお話です。たけちゃん先生の問題をベースとして、一つ面白い問題を作れることに気づきました。
それが次の問題です。

たけちゃん先生は、2次多項式の係数 を 整数 としていました。私は、それを 素数 に限定したらどうなるかを考えてみたのです。
解いてみるとわかりますが、係数を素数に限定するだけで、単純に一般の整数を考えるよりも一歩進んだ議論ができるのです。
tsujimotterの問題の解答
それでは、解答に移りたいと思います。
まず
についてですが、答えは簡単です。こちらが答えです:
は素数なので、たしかに素数係数の2次多項式です。実は、先ほど例として紹介したものが解答そのものになっていた ということでした。
というわけで、ここから先は
について考えていきたいと思います。
「素数 に対する
が整数係数の範囲で分解できる」を仮定 します。すると、
が成り立つはずです。 の部分には整数が入ります。
ここで、分解後の の係数同士をかけると
になります。
は素数より、因数は
か
しかありえません(ここで「素数」の条件が使えるわけですね)。よって、分解後の
の係数のいずれか一方が
、他方が
となります。すなわち
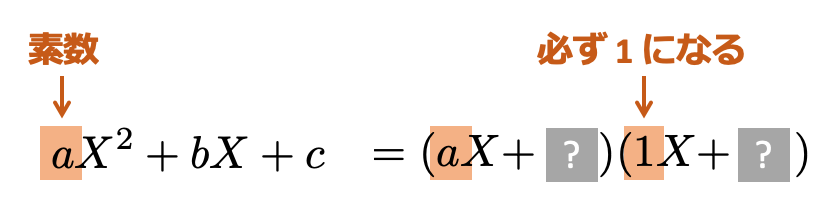
ということです。
また、分解後の定数項同士をかけると になります。
は素数より、因数はやはり
か
しかありえません。よって、分解後の定数項のいずれか一方が
、他方が
となります。すなわち
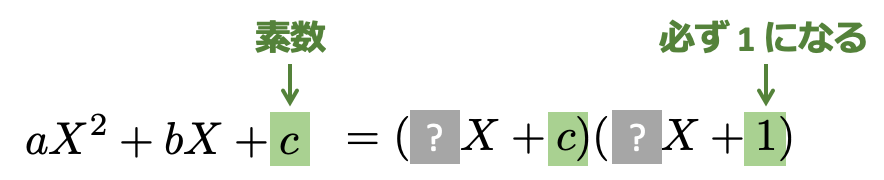
ということです。
結果的として、以下の2通りのパターンに絞ることができます。
あとは、これらの2通りでそれぞれ議論すればよいことになります。
パターン (A):
パターン (A) の式を展開すると次のようになります:
ここで、元々の条件より が素数でなければなりません。 ここで素数は、2(偶数)か3以上の奇素数のいずれかです。
もし、 のとき、
でなければなりませんが、
も素数よりこれは不適です。
一方、 のとき
という形にしかならないので、 の少なくとも一方は
でなければなりません。
ここで上の考察「 が整数係数の範囲で分解できるかどうかは、係数
を入れ替えても変わらない」を思い出すと、
は入れ替えても一般性は失わないので、
とします。
とすると、
が素数ということになります。
結局、パターン (A) のとき
ということになります。
パターン (B):
もう一方のパターン (B) の式を展開すると次のようになります:
ここで、元々の条件より が素数でなければなりません。先ほどと同様に、素数は 2(偶数)か3以上の奇素数のいずれかであることに注意します。
もし、 のとき、
でなければなりませんが、
も素数よりこれは不適です。
一方、 のとき
という形にしかならないので、 の少なくとも一方は
でなければなりません。
ここでやはり は入れ替えても一般性は失わないので、
とします。
とすると、
が素数ということになります。
結局、パターン (B) のとき
ということになります。
パターン (A), (B) のまとめ:
以上により、パターン (A) に対しては
の形の係数に限られることがわかりました。
ここで、 の組に着目します。
は共に素数でなければなりません。このような条件の素数には 特別な名前 がつけられていました。すなわち、
は ソフィ・ジェルマン素数 であり、
は 安全素数 です。つまり、ソフィ・ジェルマン素数と安全素数の組が存在すれば、それに対して整数係数に分解できる2次多項式が得られるわけです。
さて、このような素数の組は、無数に存在するでしょうか?
残念なことに、ソフィ・ジェルマン素数(および安全素数)の無限性の証明は、2020年6月28日現在 未解決問題 となっています。
一方のパターン (B) はどうでしょうか?
パターン (B) に対しては
の形の係数に限られることがわかりました。
ここで、 の組に着目します。
は共に素数でなければなりません。このような条件の素数には、やはり 特別な名前 がつけられていました。そう、
は 双子素数 の組となっています。つまり、双子素数の組が存在すれば、それに対して整数係数に分解できる2次多項式が得られるわけです。
さて、このような素数の組は、無数に存在するでしょうか?
これまた残念なことに、双子素数の無限性の証明は、2020年6月28日現在 未解決問題 となっています。
やはり、ダメだったか・・・。
今回のtsujimotterの問題は、ソフィ・ジェルマン素数の無限性 と 双子素数の無限性 のいずれか一方が成立することと同値 であることがわかりました。この問題を解決しようと思ったら、未解決問題を解かなければならない ということですね。
そういえば、昨日 6/27 はソフィ・ジェルマンの命日 だったらしいですよ。まさにこの記事を書いているときに、以下のツイートが流れてきて、驚きました。
今日は数学者ソフィー・ジェルマンの命日です。
— 和から@大人のための数学・統計教室 (@wakara_nagomi) 2020年6月27日
素数に名前を冠していることでも有名ですね。
pが素数で、2p+1も素数であるとき、pを「ソフィー・ジェルマン素数」といい、2p+1のことを「安全素数」といいます。
安全祈願のお守りとして、安全素数を持つことオススメします(笑)
というわけで、今日のお話をまとめると、
たけちゃん先生の問題 を 素数係数 に変更したら、未解決問題 になった件
でした。
意外なところから有名な未解決問題に結びついて、とても楽しかったです!
最後まで読んでくださった皆さまありがとうございました。
それでは今日はこの辺で。