本記事は「具体例を通して学ぶ虚数乗法論」シリーズ
tsujimotter.hatenablog.comの続きの記事となっています。よろしければ、上の過去の記事も一緒にご覧になってください。
さて、前回の記事では、 が 類数1 の虚2次体であるとき、
に虚数乗法を持つ楕円曲線について計算しました。類数1のケースでは、具体的に楕円曲線のリストがあったので、比較的に容易に計算できたのでした。
一方、類数2以上 の場合はどうかというと、そのようなリストは見当たりません。どうやれば具体的な楕円曲線を構成できるかというのが今回のテーマです。
今回は、類数2の虚2次体の例として、 の場合について考察したいと思います。
目次:
K = ℚ(√-5) に虚数乗法を持つ楕円曲線
類数2の例として、 の場合を考えましょう。今回の記事では、あくまで具体的に紹介することに留めて、別の記事で背景となる理屈を説明します。
まずは、次の記事で書いた j関数の特殊値の計算 を思い出します。
tsujimotter.hatenablog.com
ここでは、2つの虚2次無理数
を用意します。
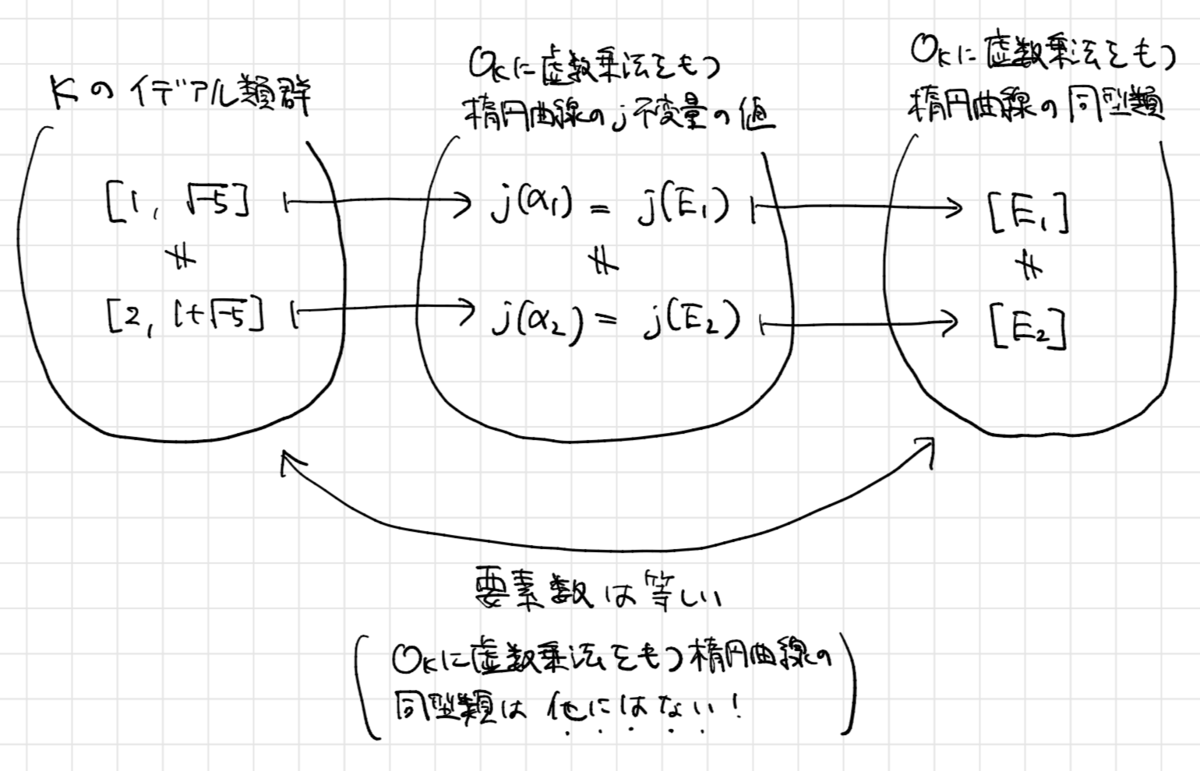
実は、これらは のイデアル類群
の2元
に対応しています。
代表元 の生成元
を割り算した
が
に対応していて、もう一方の
の生成元
を割り算した
が
に対応していますね。
これらに対応するj関数の値
を上の記事では計算しています。実際、
となることがわかります。
さて、ここで重要な情報は、上記の2つに対応するj不変量を持つ楕円曲線を具体的に構成できるということです。
これらは実は に虚数乗法を持つ楕円曲線になっていて、そのj不変量の値
は
という具合に、元々の の値に一致します。
以前紹介したように、2つの楕円曲線 のj不変量が等しいのは、
が同型な場合に限るという事実がありました。
したがって、 に虚数乗法を持つ楕円曲線の持つj不変量の値は、相異なる楕円曲線の同型類を生成します。これにより、上で挙げた
は同型ではないということが分かります。
また、 に虚数乗法を持つ楕円曲線の同型類の個数は、
のイデアル類群の位数に一致するという事実があります。
何が言いたいかというと、 に虚数乗法を持つ楕円曲線は、上の
のいずれかに同型だということです。つまり、すべて列挙したことになります。
今回は を使ってray類体を計算しましょう。そのために、
の定義方程式を変形しておきたいと思います。まず、係数を
と置きます:
左辺を平方完成して
とすることで の項を消すことができます。また、
なる変数
を導入して
とすることで、最終的に得られる右辺からは
したがって、 という変数変換によって
という形に変換できたことになります。これはray類体の計算のときに使える形式の定義方程式になっていますね。
楕円曲線 の定義方程式を具体的に計算してもよいのですが、少し面倒です。そこで、元々の
の等分点を計算して、その座標を変数変換
によって写して使用することにします。
ray類体を構成するために必要なのはウェーバー関数を通した座標であり、ウェーバー関数の定義より、必要なのは 座標だけです。
なので、
の
座標をそのまま添加しても問題なさそうですね。
というわけで、 の具体的な表示は不要であることが分かったので、以下では
をそのまま計算したいと思います。
ray類体の計算
まず、 のヒルベルト類体
を決定します。
より
ということになりますね。
楕円曲線 は、この
上定義されていると考えることができます。これをSagemathで定義したいと思います。(通常通り
上の楕円曲線として定義しようとするとエラーが出てしまうので注意。)
K.<a> = NumberField(x^2 + 5); K H.<b> = K.extension(x^2 - 5); H j = 632000 + 282880*b E = EllipticCurve(H, [1, 0, 0, -36/(j-1728), -1/(j-1728)]); E E.j_invariant()
結果は次の通りです。
Number Field in a with defining polynomial x^2 + 5 Number Field in b with defining polynomial x^2 - 5 over its base field Elliptic Curve defined by y^2 + x*y = x^3 + (-9945/2795584*b+11079/1397792)*x + (-1105/11182336*b+1231/5591168) over Number Field in b with defining polynomial x^2 - 5 over its base field 282880*b + 632000
j不変量 の値も、元々の
の値一致していることが分かりますね。
それでは、 の2等分多項式を計算しましょう。
f = E.division_polynomial(2); f
fac = f.factor(); fac
結果は次の通りです。
4*x^3 + x^2 + (-9945/698896*b + 11079/349448)*x - 1105/2795584*b + 1231/1397792 (4) * (x - 8/209*b + 73/836) * (x^2 + (8/209*b + 34/209)*x - 9/13376*b + 7/6688)
2等分多項式は
であることがわかりました。これを分解すると
となりますので、2等分点の 座標は本質的に2次拡大を生成することが分かりますね。
というわけで、2等分多項式の2次の因数を とします。
のすべての根を
に添加した体が、
上の導手
のray類体
となります。
これをSagemathの方では と名付けて計算しましょう。
g = fac[1][0]; g print("") L.<c> = H.extension(g); L print("") L.absolute_vector_space()
結果は次の通りです。
x^2 + (8/209*b + 34/209)*x - 9/13376*b + 7/6688 Number Field in c with defining polynomial x^2 + (8/209*b + 34/209)*x - 9/13376*b + 7/6688 over its base field (Vector space of dimension 8 over Rational Field, Isomorphism map: From: Vector space of dimension 8 over Rational Field To: Number Field in c with defining polynomial x^2 + (8/209*b + 34/209)*x - 9/13376*b + 7/6688 over its base field, Isomorphism map: From: Number Field in c with defining polynomial x^2 + (8/209*b + 34/209)*x - 9/13376*b + 7/6688 over its base field To: Vector space of dimension 8 over Rational Field)
上の拡大次数は
となっていて、その内訳は
となっています。
素イデアルの分解法則の確認
ray類体が計算できたので、 の素イデアルの分解法則を考えましょう。
まず、 のヒルベルト類体
の分解法則により、
の単項素イデアル
が
で完全分解することになります。
より、完全分解とは2個の素イデアルの積に分解されることを指します。
その中で特に のものが、その上の
で完全分解されることになるのです。
より、完全分解とは4個の素イデアルの積に分解されることを指します。
前回同様の注意ですが、 と表せるので、
という条件であることに注意しましょう。
よって、たとえば のように、
が
の素イデアルであれば、
においても完全分解するはずです。実際に確かめてみましょう。
K.factor(17) H.factor(17) L.factor(17)
Fractional ideal (17) (Fractional ideal (-1/5*a*b + 4)) * (Fractional ideal (-1/5*a*b - 4)) (Fractional ideal (((188/55*a + 556/55)*b - 172/55*a - 180/11)*c + (1/55*a + 28/55)*b + 4/55*a + 7/11)) * (Fractional ideal (((-36/11*a + 172/55)*b + 556/55*a - 188/11)*c + (-3/11*a - 4/55)*b + 28/55*a - 23/11)) * (Fractional ideal (((188/55*a - 556/55)*b - 172/55*a + 180/11)*c + (23/55*a - 28/55)*b + 4/55*a + 15/11)) * (Fractional ideal (((188/55*a - 556/55)*b - 172/55*a + 180/11)*c + (1/55*a - 28/55)*b + 4/55*a - 7/11))
分解の様子を見ると、 の素イデアル
は、
で2個の素イデアルの積に分解し、
で4個の素イデアルの積に分解していることが分かりますね。たしかに、
は
で完全分解することが確認できましたね。
先ほど を選んだ理由ですが、
が
で惰性するというのがその理由です。
実際、 となる
が
で惰性します。平方剰余の相互法則より
ですから
が で惰性することになります。
それでは、 なる素数のうち、特に
で惰性するものについて、
における分解の様子を調べてみましょう。
P = Primes() p = P.first() while p < 300: if p % 20 == 11 or p % 20 == 13 or p % 20 == 17 or p % 20 == 19: pk = K.factor(p) ph = H.factor(p) pl = L.factor(p) print p, len(pk), len(ph), len(pl) p = P.next(p)
11 1 2 4 13 1 2 4 17 1 2 4 19 1 2 4 31 1 2 4 37 1 2 4 53 1 2 4 59 1 2 4 71 1 2 4 73 1 2 4 79 1 2 4 97 1 2 4 113 1 2 4 131 1 2 4 137 1 2 4 139 1 2 4 151 1 2 4 157 1 2 4 173 1 2 4 179 1 2 4 191 1 2 4 193 1 2 4 197 1 2 4 199 1 2 4 211 1 2 4 233 1 2 4 239 1 2 4 251 1 2 4 257 1 2 4 271 1 2 4 277 1 2 4 293 1 2 4
いずれも で完全分解していることが分かりますね。面白いです!
おわりに
今回は、虚2次体 の類数が2の場合でも、
に虚数乗法を持つ楕円曲線の定義方程式を具体的に求められること、そこからray類体を計算できることについて紹介しました。
ちゃんと、ray類体上で素イデアルの分解法則が成り立つことも確認できて楽しかったですね。こんな風に具体的にray類体が構成できてしまうのが虚数乗法の面白さだなと思いました。
今回の方法を応用すれば、類数が2より大きいケースでも同様に計算できると思います。興味がある人はやってみてください。
次回からは、具体例の計算は一度お休みして、虚数乗法を持つ楕円曲線の一般論について紹介したいと思っています。
それでは今日はこの辺で。