二次体の分解法則と平方剰余の相互法則

前回に引き続き類体論に関するお話です。続きものなので，ぜひ以下の記事を読んでからきてください。
tsujimotter.hatenablog.com
tsujimotter.hatenablog.com

今日の主役は二次体です。二次体とは，平方因子を持たない $d$ に対して $K = \mathbb{Q}(\sqrt{d})$ の形で与えられる $\mathbb{Q}$ の二次拡大体のことです。一見簡単そうな形をしていますが，実は結構奥が深いのです。

前回の記事の最後に述べた通り，二次体の分解法則は円分体の分解法則の導出の延長線上で導くことができるのです。しかも面白いことに，二次体だけの議論ではうまくいかず，なんと円分体の理論を援用することになります。

記事の最後には，今回の話の応用として得られる

「平方剰余の相互法則」

についても触れたいと思います。平方剰余の相互法則は，二次体と円分体が密接に結びついてできた定理だと言えるでしょう。

二次体の分解法則

まずは，円分体の流れを踏まえて，二次体におけるフロベニウス自己同型を考えます。

さて，二次体 $K$ における $p$ の素イデアル分解を考え，その素因子の１つを $P$ とします（ $(p) \subset P$ です）。ここで， $K/\mathbb{Q}$ における $P$ のフロベニウス自己同型を $\left(\frac{K/\mathbb{Q}}{(p)}\right)$ とすると，フロベニウスの定義より $\alpha\in \mathcal{O}_K$ に対して

$\displaystyle \left(\frac{K/\mathbb{Q}}{(p)}\right) (\alpha) \equiv \alpha^p \pmod{P}$

が成り立ちます。ところが，このままでは先に進むことができません。

円分体とガウス和

ここでは「任意の二次体は円分体に含まれる」という事実を使って，円分体を通して二次体のフロベニウスを導くことにしましょう。

円分体と二次体をつなぐためにガウス和という道具を用意しましょう。ガウス和は，奇素数 $l$ に対して

$\displaystyle \sum_{a=1}^{l-1} \left(\frac{a}{l}\right)\zeta_l^a$

という式で定義します。この和は，すべて円分体 $\mathbb{Q}(\zeta_l)$ の元によって構成されています。

このガウス和については，ガウスが非常に面白いことを発見していて，この和を計算すると $l$ の平方根が得られることが知られています。厳密には，次のような式が成り立ちます。

$\displaystyle \sqrt{(-1)^{\frac{l-1}{2}}l} = \sum_{a=1}^{l-1} \left(\frac{a}{l}\right)\zeta_l^a$

$(-1)^{\frac{l-1}{2}}$ という少し余計な項がついてしまっていますが，ほとんど $l$ の平方根です。ルートの中身は， $l$ が $4n+1$ 型素数であれば $+l$ ， $l$ が $4n+3$ 型素数であれば $-l$ となります。

この式によって， $\sqrt{(-1)^{\frac{l-1}{2}}l}$ という数は円分体 $\mathbb{Q}(\zeta_l)$ の元によってかけることがわかります。したがって， $\mathbb{Q}\left(\sqrt{(-1)^{\frac{l-1}{2}}l}\right) \subset \mathbb{Q}(\zeta_l)$ が言えるわけです。二次体 $\mathbb{Q}\left(\sqrt{(-1)^{\frac{l-1}{2}}l}\right)$ が円分体に包まれていることがわかります。

例を挙げましょう。 $l=7$ のとき，すなわち， $\mathbb{Q}(\zeta_7)$ においてガウス和

$\sqrt{-7} = \zeta_7^1 + \zeta_7^2 - \zeta_7^3 + \zeta_7^4 - \zeta_7^5 - \zeta_7^6 \tag{1}$

を用いると， $\mathbb{Q}(\sqrt{-7}) \subset \mathbb{Q}(\zeta_7)$ という包含関係が得られます。

この例と上の式は後に使いますので，覚えておいてください。

実はもっと一般に，二次体どころか $\mathbb{Q}$ 上の任意のアーベル拡大 $K/\mathbb{Q}$ に対して，正整数 $m$ が存在して，

$K \subset \mathbb{Q}(\zeta_m)$

がいえます。これがクロネッカー・ウェーバーの定理と呼ばれる有名な定理です。

フロベニウスの遺伝

次に，この包含関係によって，円分体のフロベニウス自己同型が二次体のフロベニウスに遺伝することを示しましょう。

円分体 $\mathbb{Q}(\zeta_7)/\mathbb{Q}$ における $p$ のフロベニウス自己同型を $\sigma_p$ とします。このフロベニウス写像は $\mathbb{Q}(\zeta_7)$ の自己同型写像ですが，これを $K = \mathbb{Q}(\sqrt{-7})$ に制限したものを $\sigma_p|_K$ と書くことにしましょう。この $\sigma_p|_K$ こそが，二次体 $K$ のフロベニウス写像になるのです。

f:id:tsujimotter:20170102102815j:plain:w600

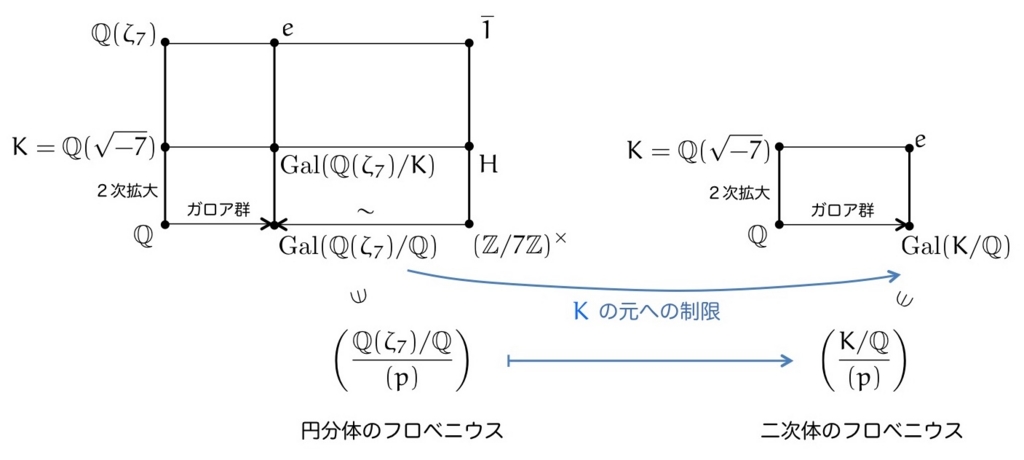
以下で示しましょう。

まず， $p$ の $K= \mathbb{Q}(\sqrt{-7})$ 上の素因子 $P$ ， $\mathbb{Q}(\zeta_7)$ 上の素因子 $\mathfrak{P}$ を $(p)\subset P \subset \mathfrak{P}$ となるようにそれぞれ１つずつ選んで固定します。 $p$ が二次体 $K$ で分解して $P$ が生まれ，さらに円分体 $\mathbb{Q}(\zeta_7)$ まで持ち上げて分解され $\mathfrak{P}$ が生まれるイメージです。 $(p) = \mathfrak{P}\cap \mathbb{Q}$ ， $P = \mathfrak{P}\cap K$ である。

すると定義から，円分体の整元 $\alpha \in \mathcal{O}_{\mathbb{Q}(\zeta_7)}$ に対して，

$\displaystyle \sigma_p (\alpha) \equiv \alpha^p \pmod{\mathfrak{P}}$

が成り立ちます。ただし， $\mathfrak{P}$ は $p$ の円分体 $\mathbb{Q}(\zeta_7)$ 上の素因子です。当然， $\mathcal{O}_K \subset \mathcal{O}_{\mathbb{Q}(\zeta_7)}$ ですから，二次体の整元 $\beta \in \mathcal{O}_K$ に対しても上の式は成り立ちます。

$\displaystyle \sigma_p (\beta) \equiv \beta^p \pmod{\mathfrak{P}}$

移行すると，

$\displaystyle \sigma_p (\beta) - \beta^p \in \mathfrak{P}$

ここで， $\sigma_p$ は二次体の元 $\beta$ のみに作用させているから， $\sigma_p|_K$ に置き換えてもかまわない。

$\displaystyle \sigma_p|_K(\beta) - \beta^p \in \mathfrak{P}$

また，左辺

$\sigma_p|_K(\beta) - \beta^p$

は，明らかに二次体 $K$ の元である。すなわち，

$\sigma_p|_K(\beta) - \beta^p \in K$

である。したがって， $P = \mathfrak{P}\cap K$ より

$\sigma_p|_K(\beta) - \beta^p \in P$

がわかり，すなわち， $\sigma_p|_K$ が二次体のフロベニウス自己同型であることがわかった。

一般に， $K \subset M \subset L$ という拡大があったときに， $M/K$ における $p \in K$ のフロベニウス自己同型は， $L/K$ における $p \in K$ のフロベニウス自己同型を $M$ に制限したものと一致します。

上の拡大体のフロベニウス自己同型がそのまま使えるということですね。二次体は円分体という「フロベニウス自己同型がわかりやすい拡大体」で上から押さえられているので，円分体の情報を使って分解法則が説明できるというわけです。円分体すばらしい。

余談ですが，私がこのことを知ったとき「最初からそれを言ってくれよ」と思ったものです。二次体を勉強しているときに円分体が例として突然現れて「難しいからあとにしよう」とほっておいたのです。二次体に円分体が関係することを知っていたら，円分体もちゃんと勉強したのになぁ。

分解法則を導く

「写像を制限する」の部分の意味がわかりづらいかもしれませんので，具体的に説明しましょう。

円分体 $\mathbb{Q}(\zeta_7)/\mathbb{Q}$ の自己同型写像 $\sigma$ を１つとってきます。たとえば，

$\sigma \colon \zeta_7 \mapsto \zeta_7^3$

としましょう。これを二次体 $K/\mathbb{Q}$ に制限するとはどういうことか。

$K = \mathbb{Q}(\sqrt{-7})$ の任意の元 $a + b\sqrt{-7}$ に作用させます。

$\sigma(a+b\sqrt{-7}) = a + b \sigma(\sqrt{-7})$

すると， $\sigma(\sqrt{-7})$ の行き先によって決まることがわかります。この行き先を決めるために，ガウス和を用いて $\sqrt{-7}$ をさらに展開していきます。

$\sqrt{-7} = (\zeta_7^1 + \zeta_7^2 + \zeta_7^4) - (\zeta_7^3 + \zeta_7^5 + \zeta_7^6)$

わかりやすいように並べ替えて符合ごとに揃えています。これに $\sigma$ を作用させて

$\sigma(\sqrt{-7}) = (\sigma(\zeta_7^1) + \sigma(\zeta_7^2) + \sigma(\zeta_7^3)) - (\sigma(\zeta_7^3) + \sigma(\zeta_7^5) + \sigma(\zeta_7^6) )$

$= (\zeta_7^3 + \zeta_7^6 + \zeta_7^5) - (\zeta_7^2 + \zeta_7^1 + \zeta_7^4)$

が得られます。これは，符合がちょうど反転していますから，

$\sigma(\sqrt{-7}) = -\sqrt{-7}$

となり， $\sigma$ は二次体 $K$ の元に対して， $\sqrt{-7} \mapsto -\sqrt{-7}$ のように振る舞うことがわかります。

実際，円分体 $\mathbb{Q}(\zeta_7)/\mathbb{Q}$ の自己同型を二次体 $K/\mathbb{Q}$ に制限すると次のようになります。

$(\mathbb{Z}/7\mathbb{Z})^{\times}$	円分体 $\mathbb{Q}(\zeta_7)/\mathbb{Q}$ の自己同型	二次体 $K/\mathbb{Q}$ の自己同型	$(\mathbb{Z}/7\mathbb{Z})^{\times}\big/H$ の類別
$\overline{1}$	$\zeta_7 \mapsto \zeta_7^1$	$\sqrt{-7} \mapsto \sqrt{-7}$	$H$
$\overline{2}$	$\zeta_7 \mapsto \zeta_7^2$
$\overline{4}$	$\zeta_7 \mapsto \zeta_7^4$
$\overline{3}$	$\zeta_7 \mapsto \zeta_7^3$	$\sqrt{-7} \mapsto -\sqrt{-7}$	$\overline{3}H$
$\overline{5}$	$\zeta_7 \mapsto \zeta_7^5$
$\overline{6}$	$\zeta_7 \mapsto \zeta_7^6$

表の上から３つ（ $\zeta_7 \mapsto \zeta_7^1, \; \zeta_7^2, \; \zeta_7^4$ ）については， $K/\mathbb{Q}$ の元を動かしません。すなわち，これらは二次体 $K$ を固定する部分群 $\mathrm{Gal}(\mathbb{Q}(\zeta_7)/K)$ （ $\subset \mathrm{Gal}(\mathbb{Q}(\zeta_7)/\mathbb{Q})$ ）となっています。また，同型定理により円分体 $\mathrm{Gal}(\mathbb{Q}(\zeta_7)/\mathbb{Q})$ のガロア群は $(\mathbb{Z}/7\mathbb{Z})^\times$ と同型でしたが， $\mathrm{Gal}(\mathbb{Q}(\zeta_7)/K)$ に対応する $(\mathbb{Z}/7\mathbb{Z})^{\times}$ の部分群を $H$ としましょう。

一方，下の３つ（ $\zeta_7 \mapsto \zeta_7^3, \; \zeta_7^5, \; \zeta_7^6$ ）については， $K/\mathbb{Q}$ の元の $\sqrt{-7}$ と $-\sqrt{-7}$ を入れ替える写像になっています。つまり，フロベニウスを２回作用させると恒等写像となります。 $(\mathbb{Z}/7\mathbb{Z})^\times$ との対応を考えると，これは $\overline{3}H$ という集合に対応しています。

つまり， $(\mathbb{Z}/7\mathbb{Z})^\times$ の部分群 $H$ による類別と $\mathrm{Gal}( K/\mathbb{Q})$ の元に全単射の対応があるということです。

$(\mathbb{Z}/7\mathbb{Z})^\times\big/H \simeq \mathrm{Gal}(K/\mathbb{Q})$

以上を二次体の分解法則の話で考えましょう。上式の右側，すなわち $\mathrm{Gal}(K/\mathbb{Q})$ は二次体のフロベニウスのとりうる範囲を示しています。一方の左側は，対応する素数の類別を表しています。このことから，二次体の分解法則がただちにわかります。

すなわち， $p\equiv 1, 2, 4 \pmod{7}$ であるような素数 $p$ （つまり， $\overline{p}\in H$ ）は，二次体 $K/\mathbb{Q}$ におけるフロベニウス自己同型の位数は $f = 1$ となる。したがって， $K/\mathbb{Q}$ において完全分解する。

一方， $p\equiv 3, 5, 6 \pmod{7}$ であるような素数 $p$ （つまり， $\overline{p}^2 \in H$ ）は，二次体 $K/\mathbb{Q}$ におけるフロベニウス自己同型の位数は $f = 2$ となる。したがって， $K/\mathbb{Q}$ において惰性する。

一般に以下の法則が成り立ちます。

二次体の分解法則

二次体を $K = \mathbb{Q}(\sqrt{d})$ とする。 $p$ を $K/\mathbb{Q}$ で不分岐な素数とし，正整数 $m$ が存在して $K \subset \mathbb{Q}(\zeta_m)$ とする。

$H$ を $K/\mathbb{Q}$ に対応する $(\mathbb{Z}/m\mathbb{Z})^\times$ の部分群とし，

${\rm Gal}(K/\mathbb{Q}) \simeq (\mathbb{Z}/m\mathbb{Z})^\times \big/ H$

が成り立つとする。このとき， $\overline{p}$ の $(\mathbb{Z}/m\mathbb{Z})^\times \big/ H$ における位数を $f$ ，すなわち

$\overline{p}^f \in H$

とすると， $p$ は $K/\mathbb{Q}$ において $2/f$ 個の素イデアルに分解する。

特に， $\overline{p} \in H$ であれば， $p$ は完全分解する。

二次体 $\mathbb{Q}(\sqrt{d})$ における $m$ はよくわかっていて， $d$ を平方因子を含まない整数としたとき，

$m = \begin{cases} |d| & (d\equiv 1 \pmod{4}) \\ 4|d| & (d \equiv 2, 3 \pmod{4}) \end{cases}$

とすればよい。実際， $\mathbb{Q}(\sqrt{d}) \subset \mathbb{Q}(\zeta_m)$ が成り立つことが知られています。

「 $4$ で割ったあまりで条件分岐が発生する」というのが二次体の非常にいやらしいところですが，こんなところに由来があったわけですね。

二次体の分解法則からつくる形

ここでちょっとブレイクして，二次体の分解法則を図形をつかって表現してみましょう。

上に例にあげた $\mathbb{Q}(\sqrt{-7})$ 上の分解法則は， $p\neq 7$ として

$p \equiv 1, 2, 4 \pmod{7} \; \; \Longleftrightarrow \;\; (p) = (X + Y\sqrt{-7})(X - Y\sqrt{-7}) \tag{2}$

と表すことができます。右辺を変形すると，

$(X + Y\sqrt{-7})(X - Y\sqrt{-7}) = X^2 + 7Y^2$

ですから，これは二次形式の形で表せます。

図形的に考えると， $p$ という素数は一辺が $X$ の正方形１つと一辺が $Y$ の正方形７つに分けられるということです。

f:id:tsujimotter:20170101170810p:plain:w500

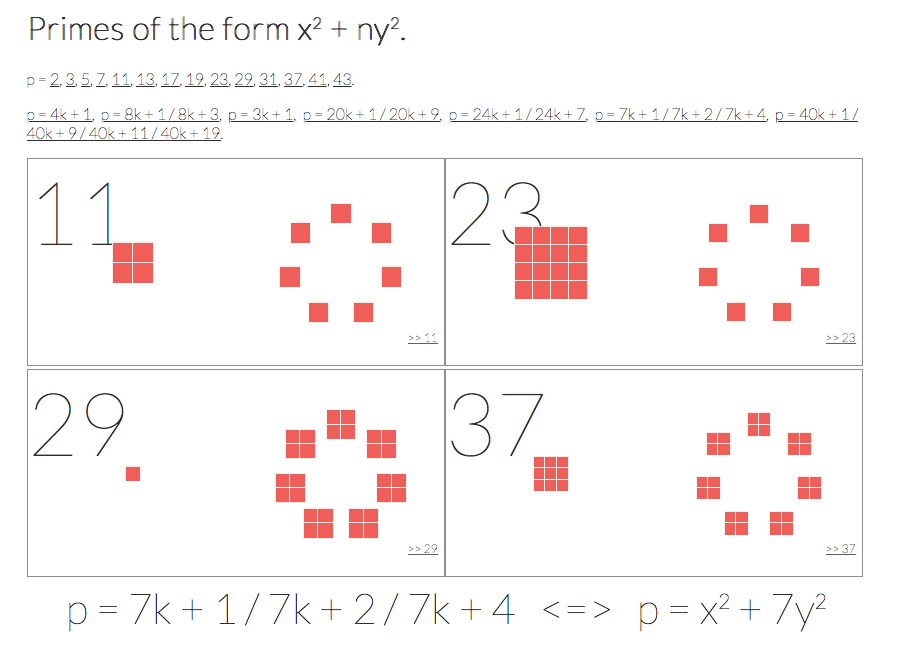
そのような分解のようすを図示したのがこのウェブサイトです。
tsujimotter.info

ほかにも， $4$ で割ったあまりの法則や $20$ で割ったあまりの法則などさまざまなタイプの分解法則を可視化しています。よかったら遊んでみてください。

１つ注意したいことは，今回紹介した可視化の方法はまだ限定された方法だという点です。上の例では $\mathbb{Q}(\sqrt{-7})$ の分解法則を扱ったわけですが，たまたま類数が $1$ の例でした。類数が $2$ 以上であれば，式 $(2)$ の右辺の素イデアルが単項イデアルとは限りません。たとえば， $\mathbb{Q}(\sqrt{-5})$ においては，類数が $2$ になってしまいます。このような問題についても，実はうまい回避方法があって類体論によって解決できます。これについては，また別の機会に話すことにしましょう。

平方剰余の相互法則

最後に，せっかく二次体の分解法則について話したのだから，応用として平方剰余の相互法則についても触れたいと思います。

平方剰余の相互法則とは，互いに異なる奇素数 $p$ と $l$ を任意にとってきたときに，その２つの間に摩訶不思議な関係が成り立っていることを主張する定理です。私のブログでもなんどか登場していて，お世話になっている定理でもあります。ガウスが証明を発見し，この定理の美しさに魅せられて７つも証明を用意してしまった話は有名ですね。実際，その７つのうちの「第４証明」が，類体論に関する証明となっており，背後にある大きな理論を数学者が発見するきっかけとなったと言われています。

平方剰余の相互法則

$p, l$ を相異なる２つの奇素数として，以下の等式がなりたつ。

$\displaystyle \left(\frac{(-1)^{\frac{l-1}{l}}l}{p}\right) = \left(\frac{p}{l}\right) \tag{3}$

ただし，両辺に登場する記号はルジャンドル記号。

左辺の $l$ にちょっと余計な係数がついていますが（これはガウス和の名残であることはすぐわかりますね），それを無視すれば素数がちょうどひっくり返っている形になっていることがわかります。もちろん，ルジャンドル記号の定義から，この法則はまったくもって明らかではありません。

ここでは，類体論をベースとした，平方剰余の相互法則の証明の概略をやってみたいと思います。ちゃんとやると大変なので，あくまで概略だけ。

さて，察しの良い方はわかるかもしれませんが，ここで挙げた素数 $p, l$ はそれぞれ以下のように対応しています。

　　 $l$ ：円分体 $\mathbb{Q}(\zeta_l)$ の次数 $l$

　　 $p$ ：円分体の部分体 $K = \mathbb{Q}(\sqrt{(-1)^{\frac{l-1}{2}}l})$ で分解される $\mathbb{Q}$ 上の素数 $p$

相互法則の左辺の記号は $p$ が二次体 $K$ 上で分解するかどうかを表しています。実際，アルティン記号を用いて

$\displaystyle \left(\frac{(-1)^{\frac{l-1}{2}}l}{p}\right) = 1 \;\; \Longleftrightarrow \;\; \left( \frac{ K/\mathbb{Q} }{(p)} \right) = e$

を示すことができます。このように比べてみると，アルティン記号ってまんまルジャンドル記号ですね。よくできています。

一方で， $\left( \frac{ K/\mathbb{Q} }{(p)} \right) = e$ という条件は，円分体の類体論により $\bmod{l}$ で表せるのでした。具体的には，上で求めた二次体の分解法則より，

$\displaystyle \left( \frac{ K/\mathbb{Q} }{(p)} \right) = e \;\; \Longleftrightarrow \;\; \overline{p} \in H$

が成り立ちます。ここで $\bmod{p}$ の条件が $\bmod{l}$ の条件に入れ替わったことに注意！

さて， $K/\mathbb{Q}$ の拡大はガウス和によって与えられていましたが，ガウス和を不変にするのは $\bmod{l}$ における平方剰余な元となります。すなわち，

$\displaystyle \overline{p} \in H\;\; \Longleftrightarrow \;\; \left(\frac{p}{l}\right) = 1$

ということです。

したがって，

$\displaystyle \left(\frac{(-1)^{\frac{l-1}{2}}l}{p}\right) = 1 \;\; \Longleftrightarrow \;\; \left(\frac{p}{l}\right) = 1$

が得られました。

これは平方剰余の相互法則そのものですね！

まとめ

平方剰余の相互法則は，私にとって憧れの定理でした。憧れの定理を一段高いレベルから理解することができて，今とても嬉しい気持ちになっています。

今回のキーポイントは，再三強調したように，円分体というわかりやすい拡大体によって上から押さえる，という点でした。そのフロベニウスを使って部分体である二次体の法則を導くことができたのでした。こんな都合のよい拡大体が二次体にはあるという点が大きいのですね。面白い。

実は，一般の $\mathbb{Q}$ 上のアーベル拡大 $K$ においても，クロネッカー・ウェーバーの定理によって円分体 $\mathbb{Q}(\zeta_m)$ に包まれることがわかります。したがって， $K$ の分解法則は，円分体のフロベニウスを用いて，まったく同じように法則化することができます。

したがって，今回の話はまさに「 $\mathbb{Q}$ 上のすべてのアーベル拡大」に対して用いることができる一般的な議論だったのです。「すべて」に適用できるというのは嬉しいですね。このような点で，円分体とそれに含まれるアーベル拡大体の理論は「 $\mathbb{Q}$ 上の類体論」と呼ばれています。

「 $\mathbb{Q}$ 上の」と注釈をつけた通り，基礎体が $\mathbb{Q}$ の場合においては円分体を用いることはできますが，一般の基礎体においては円分体では不十分です。いったいどんな拡大体を用意したら良いのでしょう。近いうちにこのような疑問を解決する１つの例についてご紹介できればと思っています。

というわけで，元日から正月っぽくない記事の二連発でした。お付き合いありがとうございます。
2017 年も楽しく数学をしていきたいと思っていますので，どうぞ宜しくお願いします。